[3D Computer Vision, Lecture 8] Absolute pose estimation from points or lines

HEEJOON MOON·2023년 2월 7일

3D Vision Lecture

목록 보기

4/6

이번 강의의 목표는 다음과 같다

1. perspective-n-point(PnP) camera pose estimation problem을 정의
2. n-point 혹은 2D-3D correspondences를 이용하여 uncalibrated camera의 camera pose를 estimate한다.
3. Grunert(3-point), Quan(4-point), EPnP(n-point) 알고리즘을 이용하여 calibrated된 카메라의 pose를 측정
4. camera pose estimation의 degeneracies에 대해 설명

Perspective camera pose estimation problem

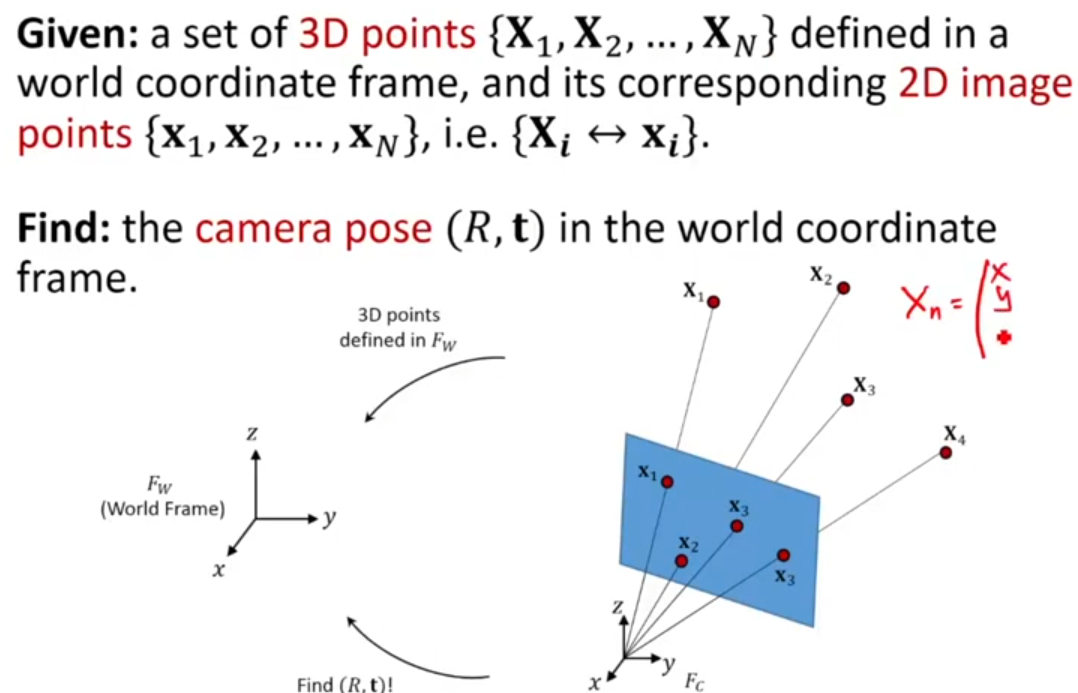
World 좌표계로 정의된 3차원 points $X_{i}$ 와 2D images에서 관찰된 점들 $x_{i}$ 가 있다고 하면, Camera pose(R, t)를 world 좌표계를 기준으로 찾아야 함.
$X_{i} - x_{i}$ : 3D-2D correspondences
위와 같은 문제를 Perspective-n-point(PnP) problem이라 함. "perspective"라는 용어는 위의 카메라 모델처럼 rays이 pinhole에 모이는 projective camera model을 사용하기 때문이다.

UnCalibrated camera: Unknown K

camera projection matrix(P)를 K(intrinsic)과 R|t의 곱으로 나타냄
2D-3D correspondences를 이용하면, unknown scale $\gamma_{i}$ 에 대해서 위의 식처럼 표현할 수 있음

위의 cross product식을 정리하면 위와 같으며, 1개의 correspondence당 2x12 matrix와 P(12x1 vector)의 곱으로 나타낼 수 있다
n개의 correspondence면 stacking하여 2nx12 matrix A와 P의 곱이 0(Ap=0)으로 표현가능
P는 11dof(12개중 1개는 scale)이므로, 최소 5.5개의 correspondence가 필요
즉 최소 6개의 point correspondences가 필요
SVD를 이용하여 Ap=0을 해결할 수 있음

Over-determined solution

Ap=0은 최소 6개의 correspondeces가 필요하지만, data가 noisy한 경우 ||Ap||의 norm이 0에 가깝게 만드는 P를 찾는다(algebric error)
SVD를 이용하여 normalization contraint을 적용하면
1) p의 norm이 1
2) || $p^3$ ||=1 -> $p^3$ 은 P의 마지막 row의 첫 3개 성분

이전 단계(algebric error)를 줄이는 방향으로 P의 초기값을 구했다면, reprojection error를 줄이는 방향으로 p를 최적화한다
이미지 plane에서 관찰된 점 $x_{i}$ 와 project된 점 $PX_{i}$ 간의 거리를 줄이는 P를 찾는다
Gauss-Newton 혹은 Levenberg-Marquardt 방법등으로 solve

내용을 summary하면 위와 같이 나타날 수 있음
1) Linear solution
a) Normalization: image point와 space point을 정규화 시곀준다
b) DLT: 2nx12 matrix A를 해결한다. Ap=0의 해 p는 ||p||=1인 제약조건하의 over-determined problem으로 해결

2) geometric error
Reprojection error를 최소화하는 projection matrix P를 찾는다. 앞선 단계서 algebra error로 찾은 P를 초깃값으로 설정

3) Denormalization
unnormalized coordinate로 다시 변환시켜준다

Unknown K with Line correspondences

3D line L이 2개의 점 $X_{0}$ 와 $X_{1}$ 을 지난다고 할 때, image line $l$ 을 back projection을 통하여 생기는 평면은 $P^Tl$ 로 나타낼 수 있다
이 3차원 평면에 점 $X_{j}$ 가 있으므로, 다음과 같은 식을 만족한다
$l^TPX_{j}=0, j=0,1$
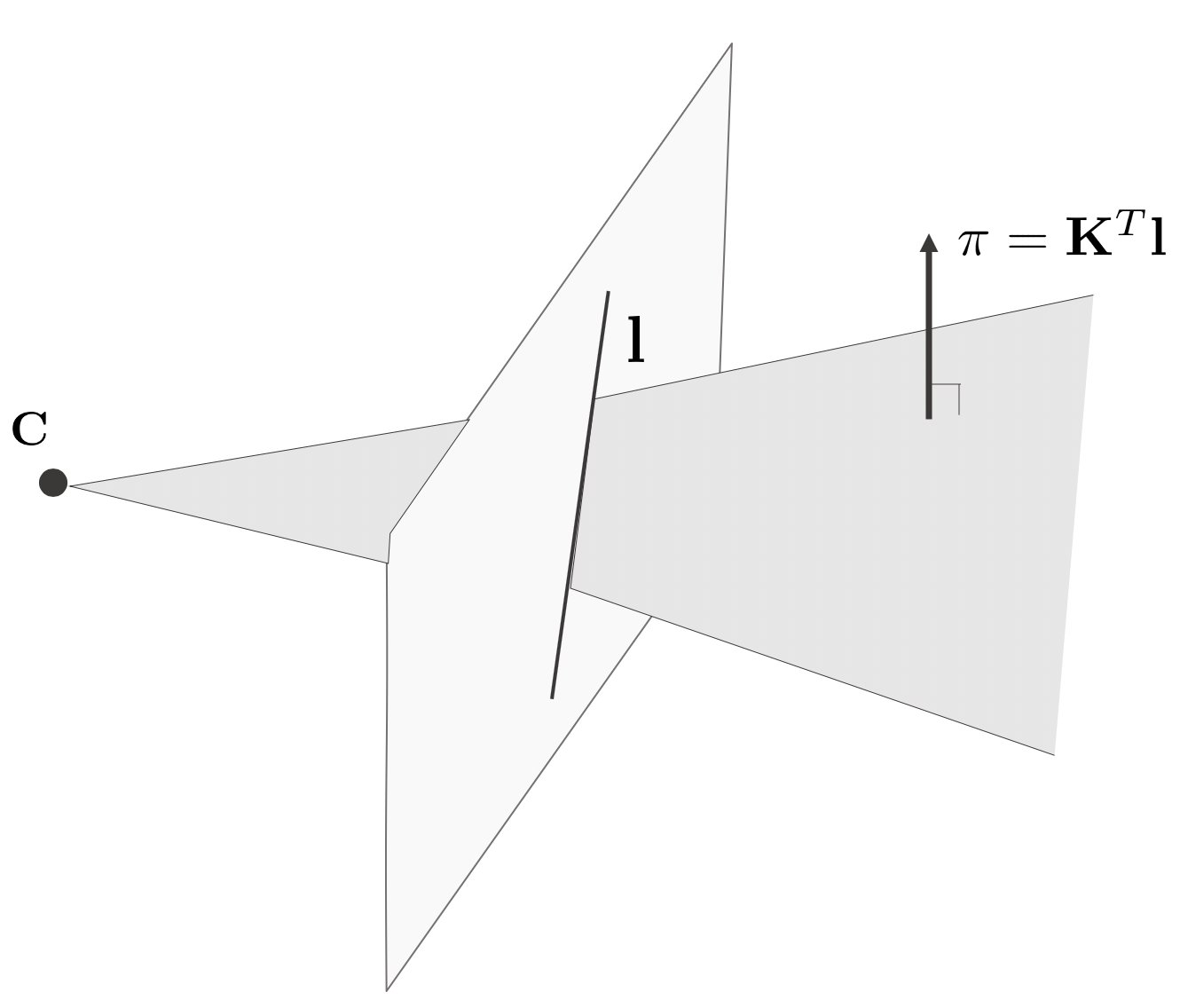
각 j마다 single linear equation이 도출되며, 2개의 방정식이 3D to 2D line correspondece마다 도출된다
$Ap=0$ from n 3D-2D line correspondence, where $A∈R^{2nX12}$ and $p∈R^{12x1}$
algebaric error ||Ap||를 줄이는 방향으로, normalization constraint을 고려하여 SVD를 이용하여 초기해 P를 구한다
geometric error: 3차원 직선 L에 있는 임의의 두점을 projection하여 얻은 두 점과 L을 projection하여 얻은 직선 $l_{k}$ 의 거리(오차)를 줄인다

Calibrated camera: known K

Intrinsic camera matrix K가 알려진 경우, two-stage로 PnP를 해결할 수 있음
1) unknown depth $S_{1}, S_{2}, S_{3}$ 를 구하기
2) absolute orientation 알고리즘을 이용하여 R, t를 구한다

(R,t)는 6자유도를 가지고, 각 correspondence는 2개의 constraints를 가진다 -> 이는 최소 3 point correspondences를 준다

Grunert Solution

3차원 공간의 3점 p1, p2, p3와 이들이 평면에 투영된 점을 각각 q1, q2, q3라 하면, perspective equation에 의해 $u_{i}=f$ $x_{i}\over z_{i}$ , $v_{i}=f$ $y_{i}\over z_{i}$

p1, p2, p3와 perspective center와의 단위 벡터는 $j_{i}$ 로 나타낼 수 있음

center에 대하여 p1, p2, p3를 단위벡터를 $p_{i}=s_{i}j_{i}$ 로 나타낼 수 있고, p1, p2, p3각각이 이루는 각을 $\alpha, \beta, \gamma$ 로 나타낼 수 있음.

cos법칙을 이용하여 수식을 위와 같이 유도할 수 있으며, 식을 정리하면 u,v에 대하여 식을 나타낼 수 있음

u와 v를 구하고 위의 식을 이용하면 s1, s2, s3를 구할 수 있다

Absolute Orientation

이전 과정에서 s1, s2, s3를 구하였다면, 3d points를 카메라 프레임에 $p'_{1}, p'_{2}, p'_{3}$ 로 나타낼 수 있으며, $p'_{i}=s_{i}j_{i}$ 로 나타낼 수 있음

rigid transformation (R,t)는 $p'_{1}, p'_{2}, p'_{3}$ $p_{1}, p_{2}, p_{3}$ 과 align시켜야 한다 (camera to world frame)

각 frame에 정의된 3점의 centroid를 구하여 빼준다. 이로 인해, 각 frame에서 정의된 점들은 centroid에 대해서 상대적으로 표현된다(translation 요소가 제거됨)

다음으로 rotation matrix를 구하기 위해서 먼저 M을 구한다
rotation matrix R은 M과 Q square의 곱으로 구할 수 있다
구한 R을 이용하여, camera coordinate centroid에 곱해주고 transition을 구할 수 있다

Degenerate Solution

Camera center p에 의해 정의된 3차원 점 $p_{i}$ 라 한다
M가 rank defiecient 해야만 degeneracy가 일어난다
Degeneracy가 발생하는 2가지 경우는 다음과 같다
1) 세 점이 동일 선상에 있을 때
2) camera center가 3점이 만드는 평면 위에 있을 때