강의 목표

1. Homography의 존재를 보임
2. algebraic, geometric, and Sampson errors를 설명하고, Homography estimation에 적용한다
3. RANSAC 알고리즘을 이용하여 robust estimation을 가능하게 한다

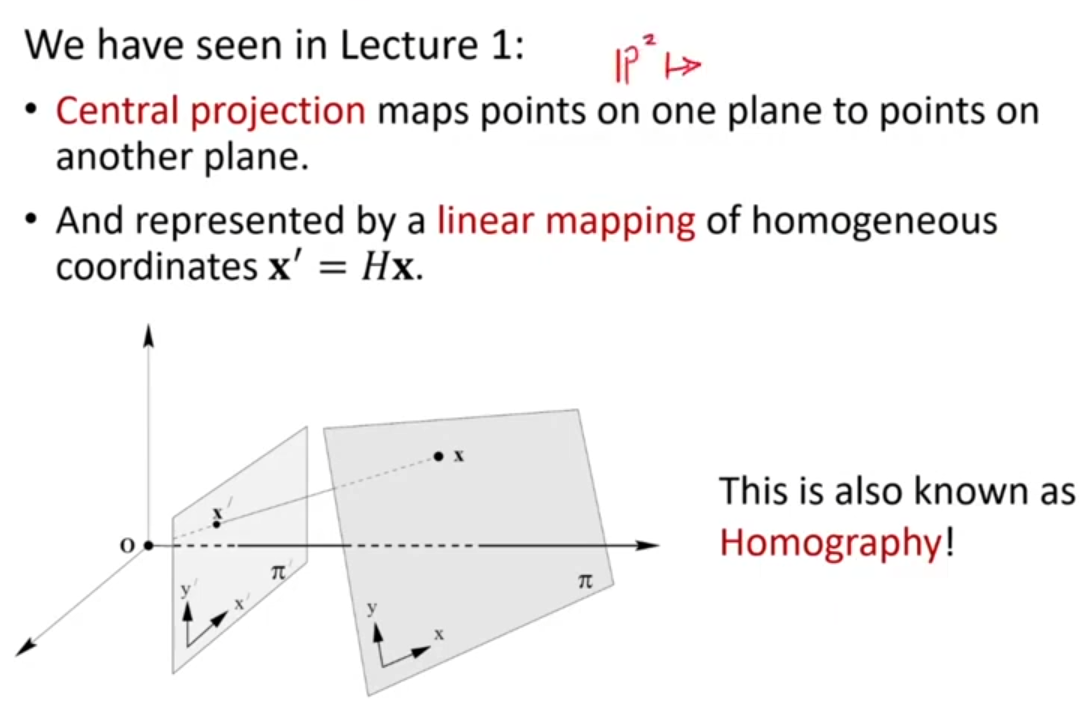
1장에서 배웠던 점 x를 x'로 linear mapping하는 것이 바로 Homogenous transformation라 할 수 있다.

• x1, x2가 3D point X를 각각 C1, C2에서 나타난 것이라고 하면, transformation에 의해 X2=RX1 + t로 표현 가능하다.
• 만약 plane $\pi$의 단위 법선벡터를 N=[n1, n2, n3]라 하면, 이 평면과 C1의 거리(d)는 다음과 같다
  $N^TX_1=n_1X+n_2Y+n_3Z=d$ -> $N^TX_1\over{d}$=1

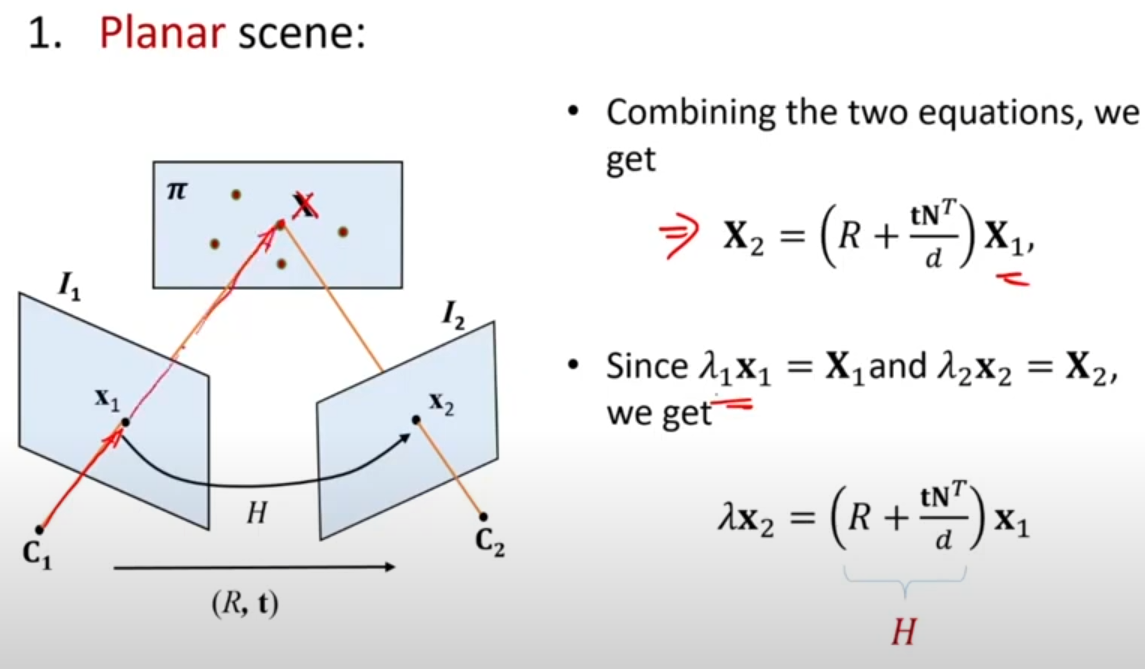
x1, x2를 각각 depth $\lambda$를 이용하여 X1, X2로 표현이 가능하며, 대입하면 위와 같은 식이 도출된다.

Infinity에 있는 평면을 살펴보면, d가 무한대가 되므로 H=R을 만족한다. 즉, pure rotation과 동일한 것이라 할 수 있다.

---

2D Homography

각 이미지에서 point의 대응관계가 주어졌을 때, H를 구하는 것이 목표이다.

Answer

• H는 8자유도를 가진다. 변수는 9개이지만, 1개는 scale에 의해 처리가 가능하다
• $x_i, x'_i$는 2개의 constraint를 가진다.

따라서 결론적으로, 최소 four point corresondences가 있어야 H 계산이 가능하다. 하지만 이것은 minimal solution이며, RANSAC을 통해서 robust한 해를 구할 수 있다.

---

Direct Linear Transformation (DLT) Algorithm

Four point correspondences $x_i, x'_i$가 주어졌다고 한다. $Hx_i=x'_i$라 하면, $x'_i \times Hx_i=0$이 성립한다.

위의 4가지 correspondences를 이용하여 h를 계산해도 exact solution을 구하는 것은 힘들다. 이는 point correspondences이 noise에 의해 corrupted 되었기 때문인데, Ah=0의 근사해를 구한 이후에 Least-Square optimization을 통해서 해결할 수 있다.

---

Data Normalization

points의 크기가 매우 큰 경우 잘못된 SVD solutions을 도출할 수 있다. 따라서 data normalization을 먼저 진행해주어야 한다. points을 normalize 하는 steps은 다음과 같이 이뤄진다.

1) points의 centroid를 origin으로 이동시킨다
2) origin으로부터의 거리가 sqrt(2)가 되도록 points을 scale한다

이를 통해 normalization 이후의 average point가 (1,1,1)이 된다. 또한 linear equation $Ah=0$에서 magnitude difference는 없다. Normalization된 점들의 DLT 알고리즘은 다음과 같이 적용될 수 있다.

---

Different Cost Functions

Algerbric distance

DLT 알고리즘은 $\epsilon = ||Ah||$, residual error라 불리는 오차를 줄이는 것입니다. 이 수치적 에러를 줄인다고 해서 geometric한 의미를 갖지는 않는다. 그럼에도 불구하고, 이것은 linear solution이며 계산적인 장점이 있습니다.

또한 algebraic distance를 이용한 해는 non-linear optimization의 초기해로 사용된다.

Geometric distance

이미지에서의 Geometric한 distance가 의미하는 것은 measured와 estimated된 이미지 좌표간의 차이를 나타냅니다. 추정된 homography H에 의해 에러는 최소화 된다.

First->Second homography H와 Second->First homography 두가지 $H, H^{-1}$을 이용해서 homography의 에러를 측정한다. 즉 변환($H$)과 역반환($H^{-1}$)의 대칭성을 이용하여 에러를 보다 정확하게 측정한다는 얘기라고 할 수 있음.

---

RANSAC: Line Fitting Example

• Given: n개의 data points
• Find: 가장 fit한 line. 직선을 예로 들면, 기울기 m과 y절편 c를 찾는 것이 대표적이다.

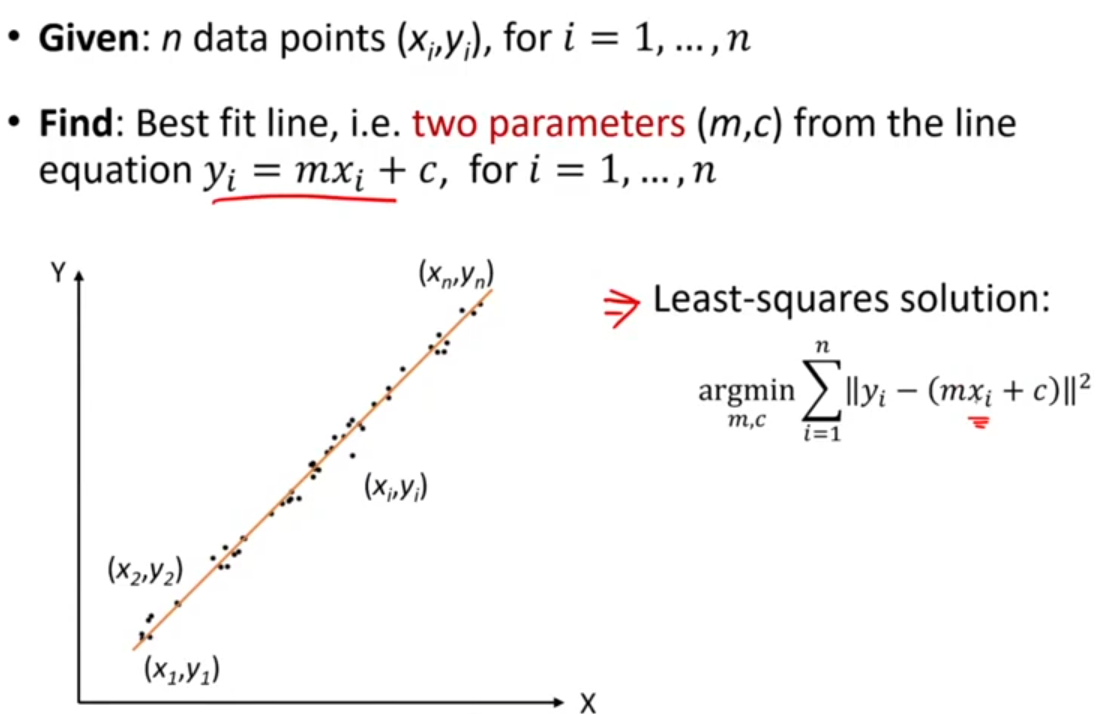
만약 data에 outliers이 많으면, Least-squares를 이용한 최적화는 실패한다.

Ransac steps

1. Random하게 points의 최소 subset을 선택한다.
2. 최소 subset을 이용하여 Model을 추정한다.
3. Error function을 계산한다.
4. Model과 consistent(inlier)한 점들을 선택한다
5. 위의 과정을 반복한다
6. Consistent points(inliers)의 수가 가장 많은 모델을 선택한다.

RANSAC 알고리즘은 3개의 파라미터가 있으며, points의 갯수 s는 모델을 정할때 필요한 점의 수, t는 오차의 임계치, N은 샘플의 갯수를 의미합니다. 즉, RANSAC을 통해 N번이 반복된다.

N을 adpative하게 선택하는 방법은 위와 같다.

따라서 Robust하게 RANSAC을 이용하여 homography estimation과정은 위와 같다. 4개의 minimal point를 선택하여 모델을 구하고, error를 구하여 thershold와 비교후 inlier/outlier를 판단. 이를 반복하여 inlier의 갯수가 가장 많이 나오는 것을 선택한다.