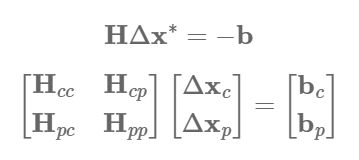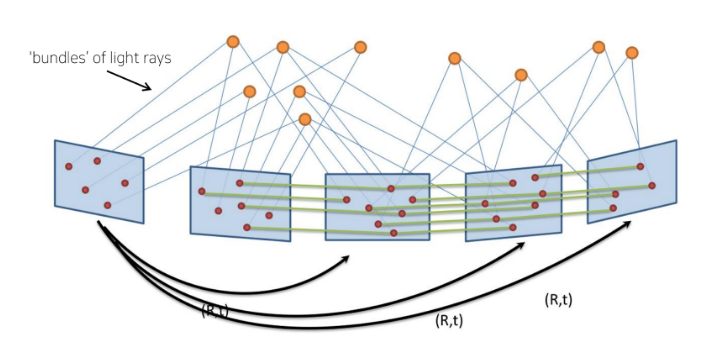
Bundle Adjustment : 다시점 이미지들로부터 복원된 3차원 공간의 특징점(Visual keypoint)들의 위치를 기반으로 3D points의 위치와 카메라 pose를 최적화하는 기법이다. 아래 그림에서 보듯이 bundle of ray, 즉 ray들을 보정한다는 의미에서 bundle adjustment이다.
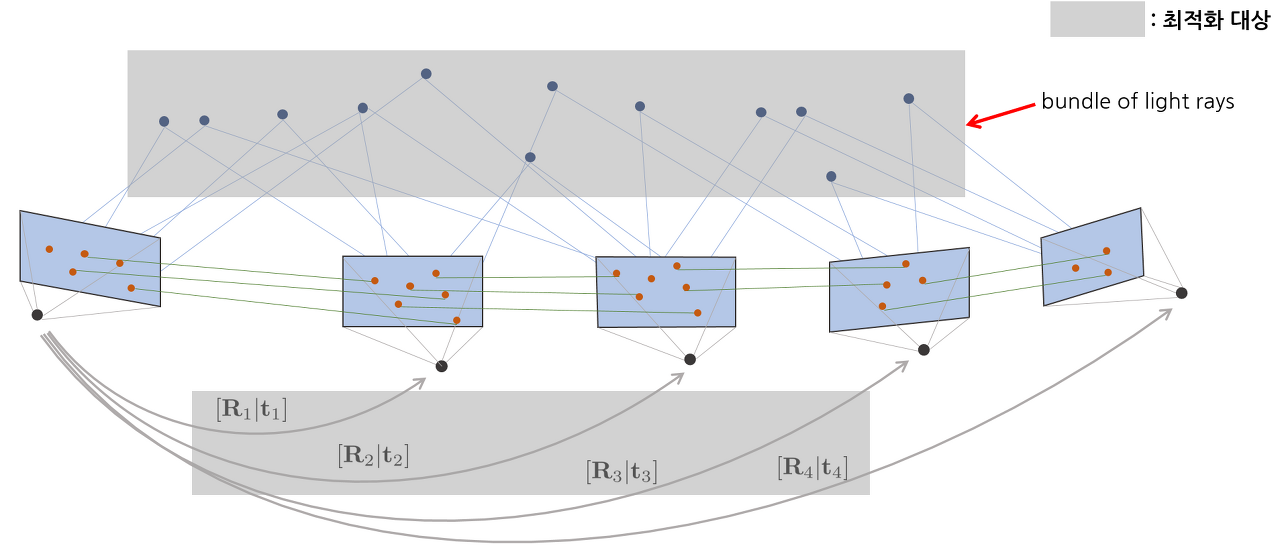
Bundle Adjustement 과정
Keypoints detection
: 특징점 검출 알고리즘(SIFT, SURF, ORB, etc.)을 이용하여 이미지에서 특징점을 추출한다. 3차원 복원시에 특징점들을 이용하여 Sparse하게 복원할 수 있으며, 이들의 3차원 위치를 추정할 수 있다. 또한 camera pose(6-DOF)를 추정할 수 있다.
Reprojection error 정의
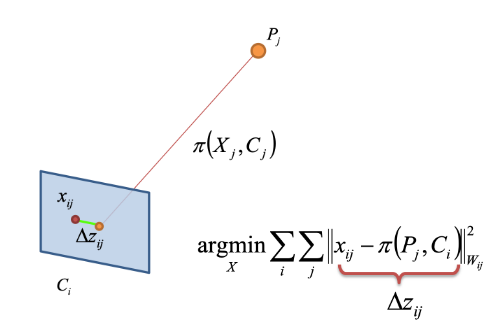
얻어낸 초기의 3D point를 camera pose에 해당하는 카메라에 대해 projection matrix를 이용하여 projection된 픽셀의 위치를 알 수 있다. 투영된 점과 실제로 measurement들 간의 차이를 이용해서 error를 계산할 수 있다. Bundle Adjustment 과정을 통해서 이러한 reprojection error를 줄이는 것을 목표로 한다.
Reprojection 에러를 다음과 같이 다시 표현해본다.
위의 projection model을 이용하여 에러는 아래와 같이 표현할 수 있다.
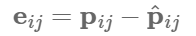
Non-linear squares 방법을 이용한 최적화
위에서 언급된 reprojection error를 줄이기 위해서는 Non-linear square 방법을 이용한다. Image-projection 과정은 Non-linear하기 때문에, Guass-Newton이나 Levenberg-Marquardt optimization과 같은 non-linear optimization을 통해 최적화해야한다.
p(j) : Projection matrix
x_ij, x'_ij : 실제 이미지에서 뽑아낸 특징점
X_i : 3D point
V_x(ij) : Reprojection error (픽셀 단위의 오차값)
Uncertainty in the image coordinates : 특징점 추출의 신뢰성 측도
이 떄 data association(3D point X_i를 이미지에 투영시켰을 때, 어떤 특징점 x_ij와 매칭이 되는지 알고 있다는 가정). 정확한 Data association이 필요하다.
Parameter 갯수
: 1개의 3D landmark당 3차원 position 3개 + Extrinsic Parameter(6-DOF) 6개 + Intrinsic parameter 5개 + Scale factor 1개 + Non-linear distortion에 대한 표현에 대한 parameter 1~2 개 = 총 16~17개의 prameter를 필요로 한다.
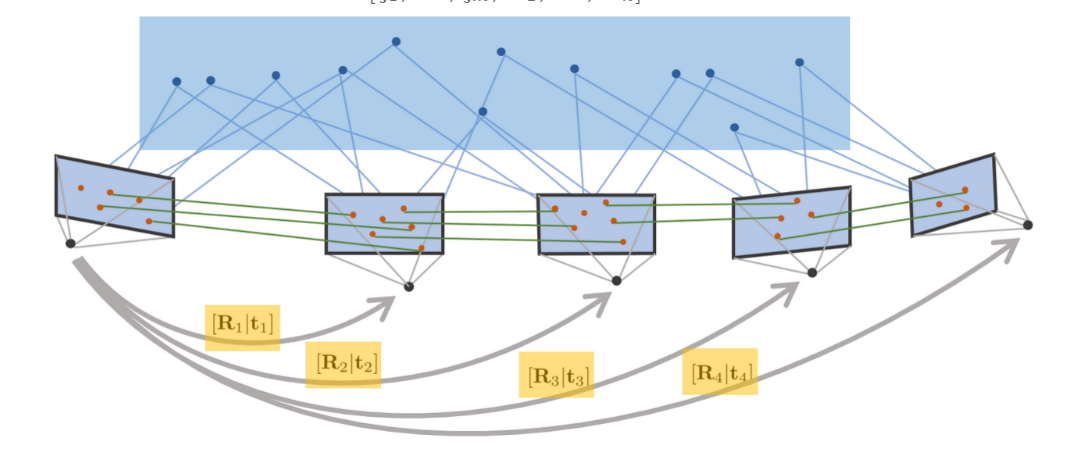
Cost function에서 최적화할 대상은 결국 camera pose와 3d position이며, 이는 아래와 같이 표현 가능하다. (m: 이미지 갯수)
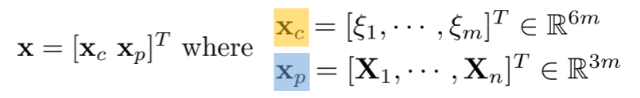
Least squres를 풀기 위해서 에러함수에 1차 테일러 근사를 수행하면 아래와 같이 자코비안 J가 유도된다.
Gaussian-Newton 방법을 예시로 들면, iteration을 수행하기 위해서는 Hx=b 문제를 풀어 interation을 위한 이동치(delta x)를 구하게 된다.
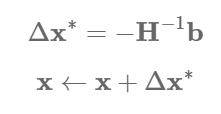
Sparsity of Hessian Matrix
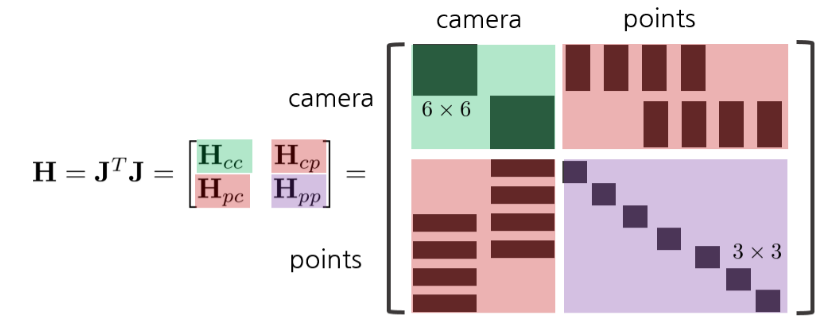
위의 과정에 언급된 헤시안 행렬은 아래와 같이 야코비안 행렬의 곱으로 표현할 수 있다.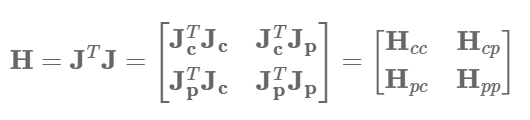 
이 때, 야코비안은 Camera pose와 3차원 점에 따라 모양이 변한다.
1개의 카메라 pose, 1개의 3차원 점이 있는 경우 야코비안은 아래와 같다
여러개의 카메라의 포즈, 3차원 점이 있는 일반적인 경우의 야코비안은 아래와 같다.
특정 카메라 pose에서만 3차원 점 Xj가 보이게 되어서, 해당 블록만 0이 아닌 값을 같는다. 따라서 위와 같은 특성을 jacobian sparsity라 하며, 헤시안 역시 야코비안의 곱이므로 sparsity를 갖는다고 한다.
헤시안 행렬은 아래와 같이 전개할 수 있다.
일반적인 경우 point의 갯수가 camera의 갯수보다 많기 때문에, 아래와 같은 형태의 H행렬이 생성된다. 이는 매우 거대하므로 역행렬을 이용하여 delta x를 구하는 경우 매우 오랜 시간이 걸리므로 다른 방법이 필요하다.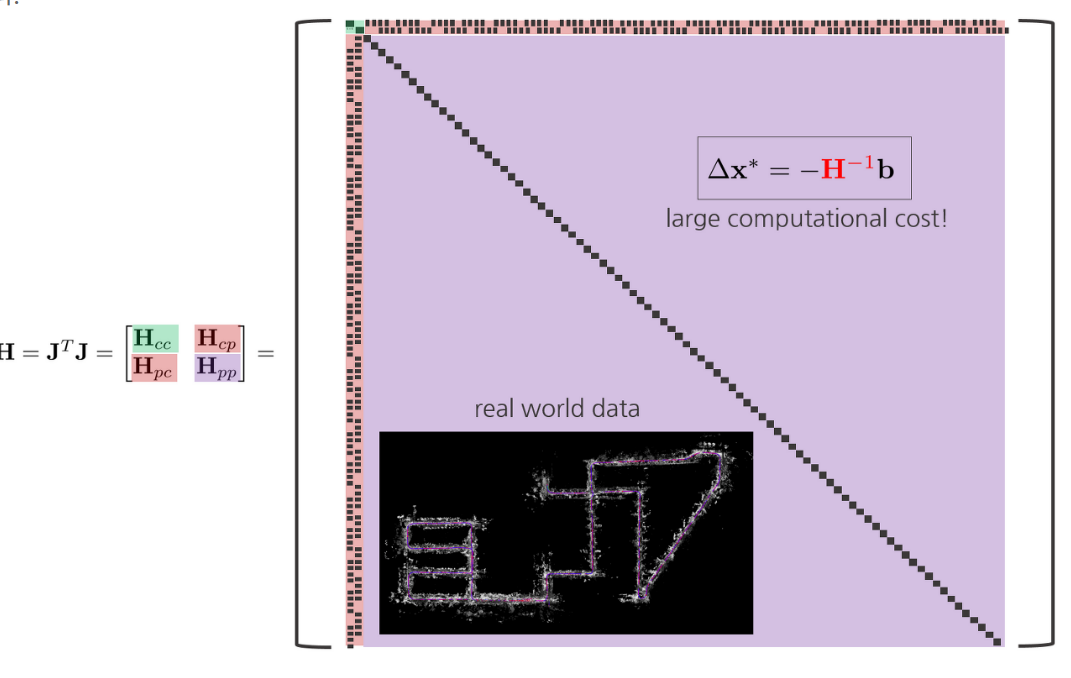 
Schur Complement (슈어 보수)
슈어보수를 이용하면 위의 문제점인 큰 연산량을 대폭 낮출 수 있다고 한다. 이 방법은 카메라 pose, point 위치의 변화량 계산을 동시에 계산하지 않고, 순차적으로 하나씩 계산함으로써 연산량을 낮출 수 있다고 한다. 
Reference
