본 논문은 line clouds라는 개념을 처음 도입한 논문입니다. line clouds란 point clouds의 각 point에서 임의의 방향(uniform하게)으로 line을 만들면, InvSfM에서 사용 불가능하다는 것을 제시하는 논문입니다.

1. Introduction

• 기존의 traditional한 Localization 방법은 2D features을 3차원 point들과 matching하는 방법이 main. 따라서 보다 persistent한 3D point clouds의 저장이 필요함

• Local features기반으로 이미지를 복원하는 방법들도 제안됨. 이후, point clouds에서 장면을 복원하는 것도 가능해지면서, privacy-preserving의 위협이 커짐. 하지만 아직 이러한 issue는 무시되어 왔음.

• 저자는 크게 다음과 같은 3가지 상황에서 Privacy-Preserving 기법이 사용될 것이라 함.
  1) Scene자체가 기밀 사항일때
  2) Scene에서 일부 secret object나 정보가 존재할 시
  3) Device에서 localization을 할 때, 서버와 연결하여 사용하는 경우 노출되기 쉬움

• 본 논문서 제시하는 방법으로는 Privacy preserving image-based localization이다. 위 방법의 목표는 3D map을 condifendial하게 보관하면서도, robust, accurate한 localization 능력이 되어야 함. 본 논문이 방법을 제시한 첫번째 논문이라 함

• Solution의 핵심 아이디어는 map 표현방식을 새롭게하여 geometry를 혼동시킴. 즉, 3차원 포인트가 line으로 대체되는 것. 위 방법은 오직 3차원 선들과 연관된 descriptors만 저장하게 된다. 위와 같이 저장된 것을 3D line clouds라 명명.

• 본 논문에서는 먼저 input이 single image일 때의 경우와 이것을 일반화하여 다수의 이미지들을 jointly localizing하는 곳에 사용

Contribution은 다음과 같다고 함
1) Privacy preserving image-based localization 문제를 제안하고 이에 대한 해결책을 제시함
2) 새로운 3D map representation을 제시(line clouds)
3) 이미지의 2D points의 3D line간의 correspondences를 구하는 최소해결책을 제안

2. Related work

Image-Based Localization

• Learning based와 같은 많은 image기반의 localization 방법들이 개발되었으나, privacy-preserving을 다룬 연구는 없었음

Privacy-Aware Recognition

• 이 분야는 대초에 secure하게 face detection을 하는 것에서 비롯됨
• privacy와 관련된 모든 CV 연구들은 recognition 문제들만 다루는 반면, 본 연구는 geometric vision을 다루는 첫 연구임

Generalized Camera Pose Estimation

• 3D line clouds를 이용한 privacy-preserving camera pose estimation은 generalized 된 카메라들과 깊은 연관이 있음
• 3D line clouds에서는 1개의 핀홀은 가진 generalized 카메라들이 1개의 3D line과 연관되어 있다는 얘기

3. Proposed Method

3.1 Traditional Camera Pose Estimation

• Reconstructed된 3D scene에서 pinhole 카메라를 localize하는 방법으로는 이미지에서 관찰된 normalized된 2D observations와 3차원 점간의 대응관계를 구하여 absolute pose인 P=[R T]를 추정하는 것이다. 이것이 PnP 알고리즘.

• P는 6개의 unknown parameters이 존재. 또한 대응 관계서 outlier가 있기 떄문에, RANSAC을 이용하여 robust하게 함.

이는 다음과 같이 $\hat{P} = argmin_{P}||\bar{x} - P\bar{X}||_{2}$의 수식으로 표현이 가능.

• Non-linear least-square 문제를 해결하면 $\hat{P}$를 구할 수 있음

하지만 위의 방법은 3D point cloud X의 정보가 주어져야하므로, privacy가 노출될 수 밖에 없음.

3.2 Privacy Preserving Camera Pose Estimation

3D point clouds를 가리기 위해서, 각 3차원 점을 점을 지나는 3차원 선으로 대체한다. 이때, 선들의 방향은 random direction($v∈R^3$).

• 3차원 선 L을 Plucker coordinate으로 표현하면 다음과 같다.
  

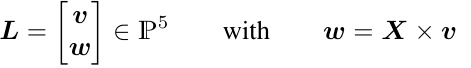
• v의 방향이 임의로 결정되었고, 외적 연산은 rank-deficient한 operation이기 때문에 유일해를 결정할 수 없어서 3차원 점 X의 정확한 위치를 파악하기 어렵다.

• 우리가 알 수 있는 사실은 3차원 공간에서 L이 점 X을 지난다는 사실과, projection되서 2차원에서도 $l$이 $x$를 지나는 것이다. 이를 이용하면 다음과 같은 제약조건이 나온다함(근데 왜 이런지는 이해가 안됨/....)

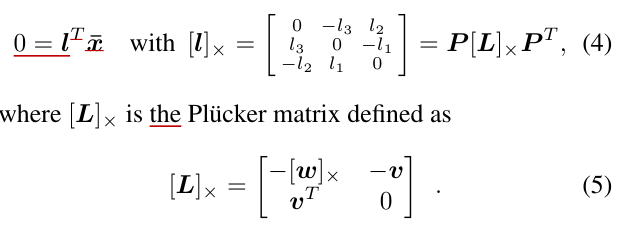
• 위와 같은 제약조건에 의해 6개의 P의 unknown parameters를 찾기 위해서 최소 6개의 correspondence가 필요하다고 함.

• 이는 기존의 PnP 알고리즘이 최소 3개의 correspondences를 필요(p3p)로 하는 것과 대비적. 저자는 pnP처럼 line cloud를 이용한 관계를 pnL이라 명명. 최소 p6L이 필요로 함.

• pnL문제를 해결하는 것은 x와 pinhole을 지나는 ray들을 rotate, translate하는 것과 같다.

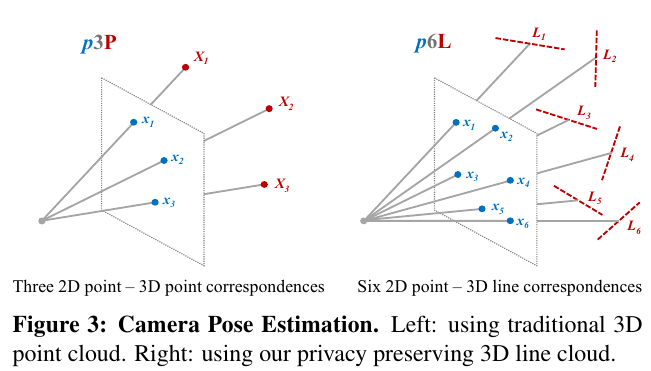
• 각 3차원 점 X에서 선 $L_{i}$들이 지나간다고 하면, 6개의 직선들의 image plane으로 project 되어도 점 $\hat{x}$를 지나야 함.
• 따라서 투영된 직선($l$)과 점$\hat{x}$ 와의 거리를 최소화하도록 P를 찾는다

3.2.1 Generalization to Multiple Cameras

• Multiple camera 시스템에 대해 적용해 봄.
• Multiple camera의 joint localization은 single과 parameterized 관점에서 다르다
  $P = P_{c}P_{m}$ with $P_{m}=s_{m}\begin{bmatrix}R_{m}&T_{m}\\0&s_{m}^-1\\ \end{bmatrix}$
• $P_{c}$: 각 카메라에 대한 relative extrinsic calibration

Privacy preserving setting에서, multiple images에 대한 generalization은 generalized relative pose problem을 해결하는 것과 같다.

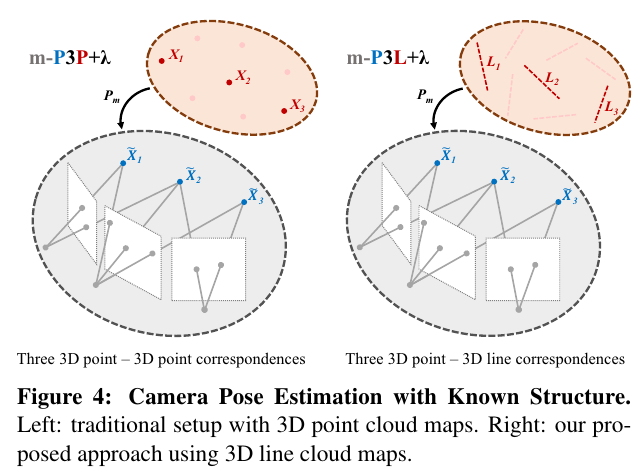
3.2.2 Pose Estimation with Known Structure

• image observation $x$에서 depth($\lambda$)를 이용하여 3차원 structure X를 추정하는 것은 $X' = \lambda\hat{x}$

• Therefore, Camera pose(P)는 카메라 좌표계에서 정의된 X'와 World frame으로 정의된 $\overline{X}$의 관계를 이용하면, $0 = X' - P\overline{X}$로 표현할 수 있다.

• Privacy-Preserving approach에서는 3D line L이 3D points $X'$을 지난다. 이것을 foramlize하면, $0 = X' - P\begin{bmatrix}v * w + \alpha v\\1\\ \end{bmatrix}$

• m-p6L 알고리즘을 이용하면, 최소 경우로 해결할 수 있음.
  

3.2.3 Extenstion to Unknown Scale

3.2.2에서 설명한 내용은 부정확한 3차원 위치 X와 X'를 다룸.

• X와 X'의 scale이 다른 경우, scale을 고려한 3D similarity transformation sP를 추정이 필요. 앞서 언급한 제약조건을 다시 적으면 $0 = X' - sP\overline{X}$

• 플루커 벡터를 이용하여 표현하면 $0 = X' - sP\begin{bmatrix}v * w + \alpha v\\1\\ \end{bmatrix}$

• 7-DOF의 3D similarity(sP)를 구하기 위해서 우리는 최소 4개의 correspondences를 구해야 함

4. Experimental Evaluation

• Ground-truth가 있는 real-world data를 가지고 실험을 수행
• 기존의 Localization방법과 line clouds를 이용한 Pose estimation performance를 accuracy/recall, robustness로 측정

Datasets

• 15개의 real-world 실내외 datasets(mobile phone이나 HoloLens)을 이용
• map images: 3D point cloud를 복원하는데 사용
• query images: 완전히 다른 viewpoint에서 얻은 이미지로서, localization 성능을 측정하는데 사용된다
• COLMAP SfM 파이프라인을 이용하여 sparse 3D reconstruction, camera calibration을 진행

Metric

• Rotation error와 translational error를 계산하여 이용
• 또한 reprojection errors를 측정

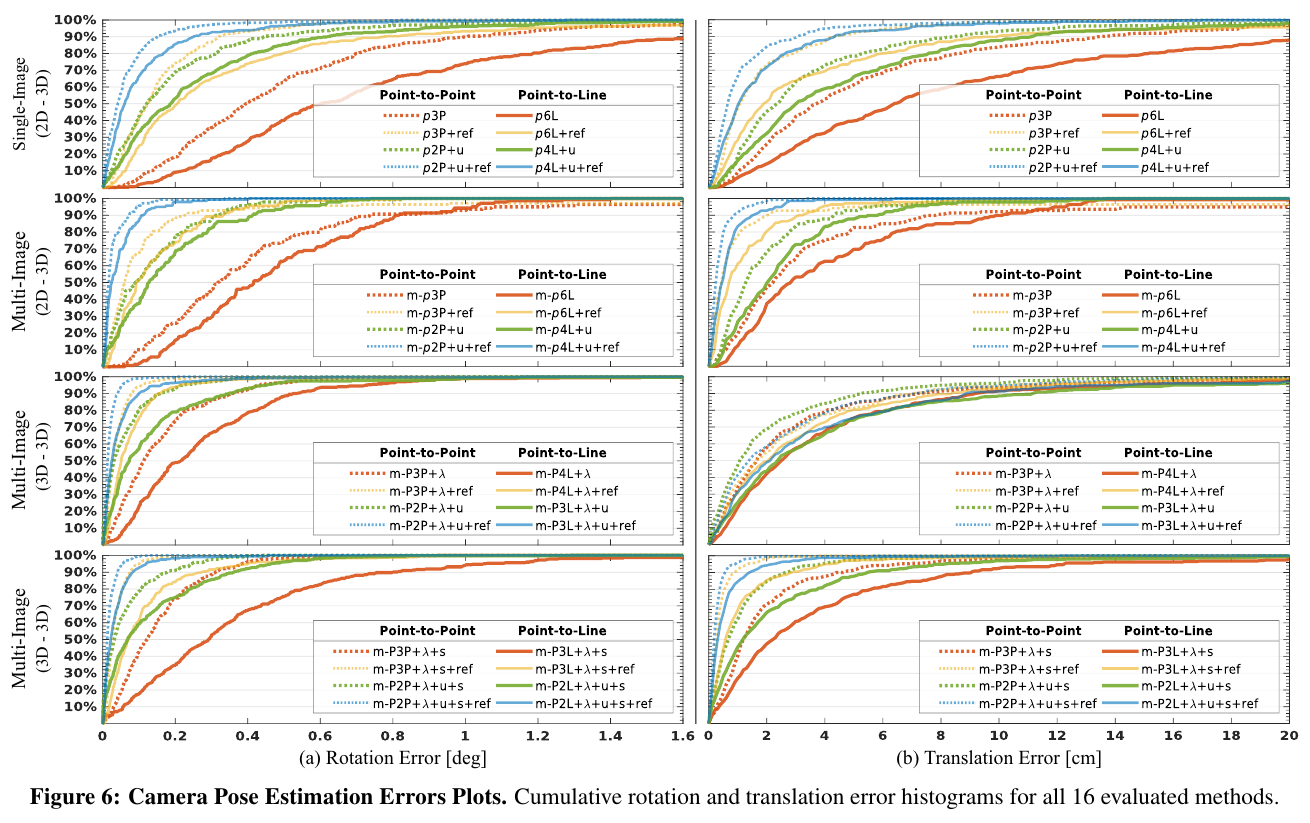
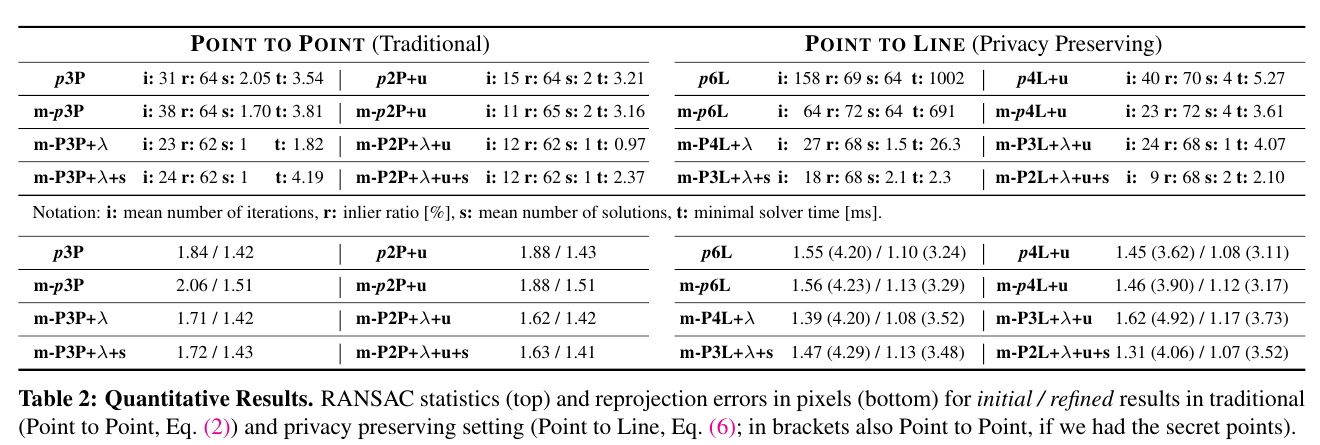
Results

• 기존의 Localization 방법과 비교하여, line clouds를 이용한 localization도 좋은 성능을 보임
• structure, gravity, scale등이 추가적으로 제시되면, 더 성능이 좋아짐

5. Discussion

• Lifting tranformation은 전체 동안 1번만 이뤄져야 한다. 그렇지 않으면, 여러버전의 lifting을 가지고 있는 것으로 역으로 점을 추정 가능

• 3D line cloud의 density를 분석하면, scene에 대한 information을 recover할 수 있다.

• 3D line clouds가 scene geometry를 혼동시키는 것처럼 보이지만, 실제로는 scene의 3차원 point의 sampling density와도 연관이 있다고 할 수 있다