• 본 논문에서는 privacy-preserving localization을 위해서 sparse한 point clouds를 그대로 두는 것이 아닌, line clouds라는 개념을 제시하며, 3차원 geometry 정보는 보존하면서도, 3D points position을 recover 가능하다고 합니다

1. Introduction

• 기존의 classical한 Visual Localization approaches은 SIFT와 같은 local features기반의 방식이 존재한다
• Traditional한 방법들은 efficient 혹은 memory limit에 초점을 두었으므로, privacy 측면은 고려되지 않았다
• SfM의 sparse한 point clouds를 이미지로 변환하는 방법들이 제안되었음. 이로 인해 더욱 더 prviacy 위협이 커짐
• 이를 막기 위해, points를 lift하여 line으로 만드는 방법이 제안되었음. 이를 line clouds라 명명하며, 이를 이용하면 여전히 localization이 가능한 것을 보임.

본 논문은 앞서 제시된 line clouds를 이용하더라도, 3차원 points의 위치를 정확하게 복원이 가능하며, 이미지를 다시 복원할 수 있다는 것을 보이는 연구입니다.

2. Related Work

Visual Localization

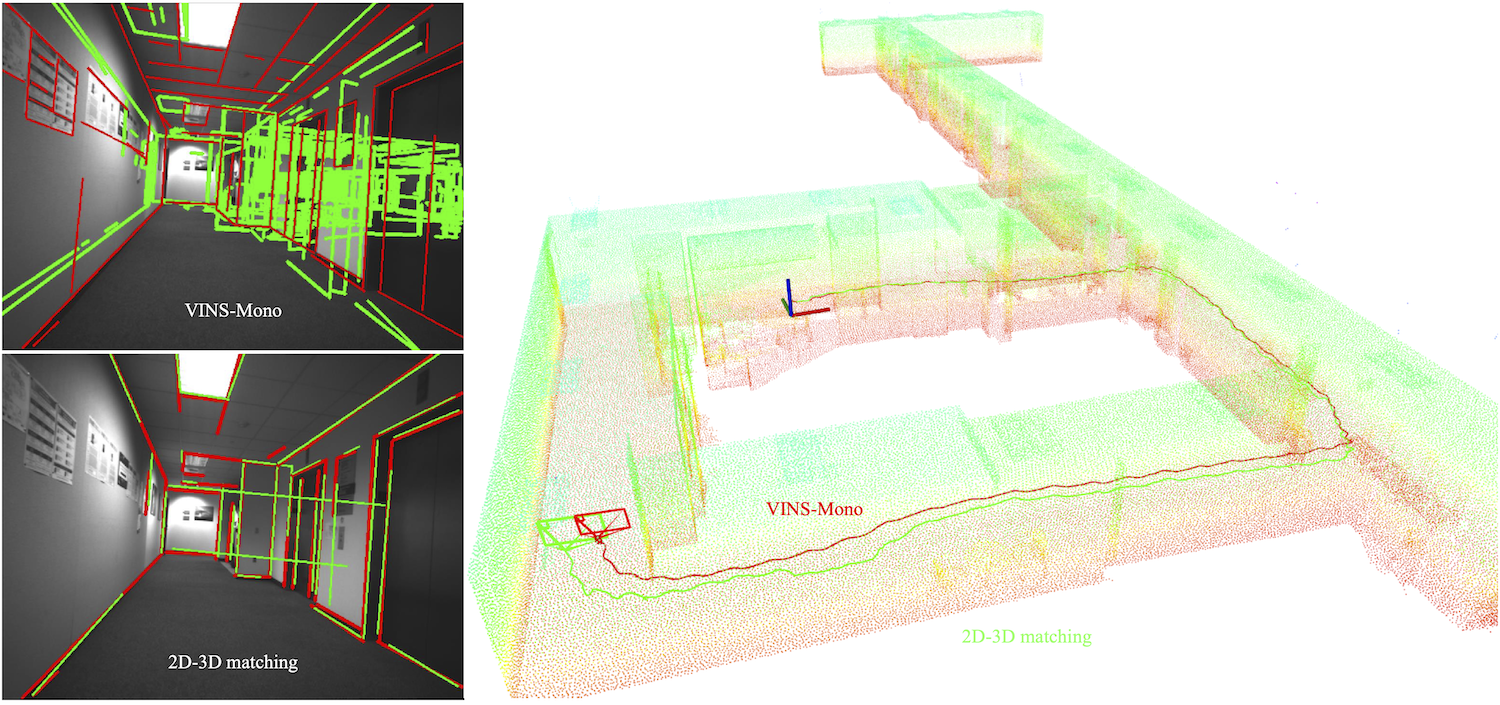
기존의 traditional한 방법중에서 가장 많이 사용되는 개념으로는, 2D-3D matching이라 할 수 있다. 이미지의 local features를 추출하고, SfM을 통해 얻은 3D points과 매칭하는 것이 대표적이라 할 수 있다. (아래 그림 참고) 이는 Image Inversion에 여전히 취약함을 알 수 있다.

• Learning기반의 localization 방식들은 기존의 방법들을 대체할 수 있음. test image의 픽셀에서 3차원 좌표를 regress하거나, CNN을 이용하여 바로 카메라의 pose를 예측하는 방법등이 있음.

• 하지만 이러한 방법들은 small scale에서만 잘 작동하므로 실제로 사용하기 어려움

Recovering image content from features

• Gradient-based features(SIFT, HOG등)을 이용하여 이미지를 복원하는 것이 가능하다는 것이 보여짐
• CNN을 이용하여 이미지를 복원하는 것이 복원의 질을 높인 다는 것이 보여졌고, 이는 추후에 이미지를 features로 부터 복원하는데에 사용됨

Privacy-preserving visual localization

• 3D points의 projection, local features를 이용하여 이미지를 합성하는 CNN이 제안됨
• Privacy preserving localization을 위해, 각각의 SfM 점을 그 점을 random한 방향으로 통과하는 선으로 대체한다.(이를 line clouds라 명명) 방향은 구의 모든 방향으로 uniform하게 샘플링된다.
• line clouds를 이용하여도 camera pose estimation이 가능하다. Line clouds를 사용하면 InvSfM을 사용할 수 없게 된다는 주장.
• 본 논문에서는 3차원 점을 line clouds로 대체하는 주장을 탐구. 결론적으로, line clouds를 이용하여 image단위의 details를 복원하는 것이 가능하다.
• 2개의 3차원 직선과 가까운 점이 실제 original한 점과 가깝다는 관찰. 따라서 이를 통해 원래 3차원 위치를 복원할 수 있다는 소리다.

3. From Point Clouds to Line Clouds

• 기존의 Structure 기반의 visual localization approaches은 주로 2D-3D correspondence(주어진 쿼리 이미지의 픽셀과 3차원 점)을 이용하여 camera의 pose를 예측

• Classical feature-based approach => $P = (p_{i}, d_{i}), P_i$는 3차원 점의 위치를, $d_{i}$는 image feature의 descriptor를 의미.

• InvSfM 논문에서는 SfM을 통해 얻은 points clouds를 가지고, feature-based localization 시스템을 이용하여 invert하는 것을 보임

• Line-clouds 논문에서는 underlying point cloud $P = (p_{i}, d_{i})$를 line cloud인 $l_{i}$로 대체한다. 3차원의 line은 사영되어도 2차원의 line이 되므로, InvSfM의 적용이 불가하다.

• Line-clouds 논문의 저자들은 "3D line의 표현으로 내제되있는 geometry 정보를 숨기고, 민감한 정보를 막을 수 있다"고 결론.

• 하지만 본 논문에서는, 위의 결론을 뒤집는다. 즉, 만약에 line의 방향이 균등하게 샘플링되었다면, 이는 기저된 기하학적 정보를 완전히 가릴 수 없다고 주장

그럼 위 논문의 방법을 방향이 균일하게 샘플링 될 때만 가능하다는 소리인 것 같다.

4. Recovering Point Clouds from Line Clouds

• 하나의 선만을 고려하면, 선을 따라 모든 후보가 점의 candidate이 될 수 있으므로 privacy-preserving

• 하지만, 다른 선을 고려하기 시작하면 선에서의 분포가 균등하지 않아짐. 이는 원래의 point clouds들이 고루 분포하지 않고, 표면에만 존재하기 때문

• 이 논문에서는, line cloud에서 local neighborhood의 정보를 복원하는 것이 가능하며, 이를 통해 line에서 3차원 점을 복원이 가능하다고 보임

• line cloud는 점들에 의해 그려진 선들의 방향에 의해 특징화 된다.

• Speciale et al은 line directions을 독립적이고 random하게 샘플링하며, localization accuracy를 유지한다. 이를 uniform line clouds라 명명한다.

위의 그림은 다음 내용을 summarize 한 것이다. 하나의 선을 기준으로 이와 이웃한 선들과 거리가 가장 가까운 점들을 구하고, 이를 분포시켜서 high-densitiy한 영역이 original 3d point의 위치라고 추정할 수 있다. 또한 저자는 이를 위해서는 Neighbourhood Estimation이 중요하다고 한다.

4.1 Information in Uniform Line Clouds

: 이 섹션에서는 2개의 3차원 선과 가까운 점이 원래의 3D point와 close하다는 것을 설명하는 part

$p(P|L) = P(L|P)P(P) \ P(L)$ : Bayes rule

모든 line directions이 독립적이므로, $p(L|P) = ∏_{𝑖=1}^N 𝑝(l_{𝑖} |p_{i})$

$𝑝(l_{𝑖} |p_{i})$는 모든 방향에 대해 균등하므로 constant. 따라서 $p(P)$를 극대화. 하지만 이는 어려운 문제이므로, global point clouds에서 구하는 것 대신, local neighborhood에 대해서 추정.

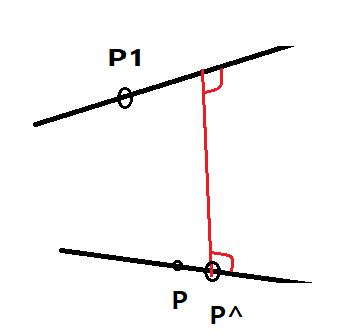
위의 그림의 경우처럼, 두개의 3차원 점 P와 P1이 있고, 그 점들을 지나는 직선 l과 l1이 있다고 가정. 선 l에서 l1과 가장 가까운 거리의 점을 P^이라 한다.

• random Variable X = d(p,p^) / d(p,p1)라 가정.
• d(p,p1)=1로 두고, X의 CDF를 구하면 아래돠 같음
  
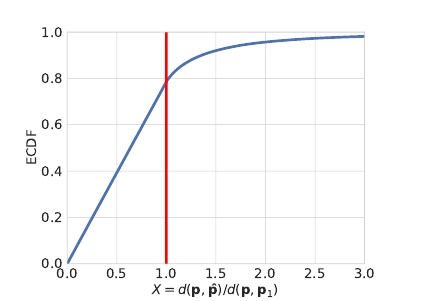
• X < 1 (p^이 p1보다 p에 가까운 경우)의 누적 확률 분포가 더 높다는 것을 확인 가능.
• 이를 통해 d(p,p1)이 작으면 p^을 보다 p에 가깝게 추론할 수 있다는 소리.

위의 상황을 k개의 이웃한 점을 통해 확장 가능.

• $d_{max} = max_{j∈N^k (p)}d(p,p_{j})$ -> 선 l의 점 p와 가장 멀리 있는 점 $p_{j}$간의 거리
• k개의 이웃한 점이 있으므로, ${l_{1}, l_{2}, ..., l_{k}}$까지 총 k개의 estimation을 구할 수 있다. 위의 그래프를 포면 X=1일 때 까지의 누적확률이 0.8이고 이를 통해 0.8k개의 점들이 $d_{max}$안에 존재할 것으로 추측.
• 만약 $d_{max}$가 작다면, 이것은 실제 점p와 가까운 cluster를 만들게 된다.

위의 내용을 결론짓자면, k개의 이웃한 점에 대해서 정보(거리)가 주어지면, 비교적 정확한 3d point(P)의 위치를 추정할 수 있다. 본 논문에서는 k=50개의 이웃한 점들을 이용하여 point를 추정해보았다고 한다.

• 또한 추정치들의 median만을 이용하거나, 이웃한 line들을 각각 50%, 90% 대체하였던 결과도 아래 그림처럼 제시하고 있음.
  

4.2 Recovering Points from Uniform Line Clouds

3D points를 추정하기 위해서 다음 2가지 stage를 거친다

1. neighborhood estimation

• 첫번쨰 iteration에서는 line-line 간의 거리의 계산과 이를 기반으로 이웃한 점들을 선택한다. 이는 Coarse하게 평가된 neighborhood이며, 이들을 기반으로 먼저 estiamtes를 구한다.

• 이를 통해 Coarse한 Position estimates를 구할 수 있음.

• 이후의 iteration부터는 추정한 point의 위치를 기반으로 이웃한 점들을 선택할 수 있다

2. Peak finding
   : 1단계에서 얻은 point의 candidates을 가지고 2단계서는 하나의 후보를 선택한다. 이는 peak finding라 하며, 선에서 candidates 분포의 high-densitiy region을 찾는다

• $\hat{p}_{ij}$는 선 $l_{i}$위에 있으면서 다른 선($l_{j}$)와 가장 거리가 가까운 점들이다. 이들을 다음과 같이 parameterize할 수 있다.
  

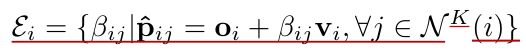
• 결국, 선 $l_{i}$위의 임의의 점 $o_{i}$와 직선의 방향벡터 $v_{i}$를 이용하여 표현 가능하다. 결국 $\epsilon_{i}$의 분포가 가장 high한 곳이 실제점 $P_{i}$의 위치라 할 수 있다는 소리.

결국, 2가지 step이 반복되면서 Coarse한 Position estimation에서 Refine되면서 Final Estimate을 구하면 Ground Truth와 유사해진다는 소리!!

4.3 Limitations

• 이 논문에서 제안한 방법의 한계로는 sparse line cloud에 대해서는 복원이 어렵다는 것이다

• line이 sparse해 질수록, true neighbors를 찾기 어렵다는 문제가 있다. 만약 true를 찾는다 해도, line의 거리가 멀어질수록, 원래의 점과 candiate의 거리가 멀어지므로 peak finding이 어렵다.

• Original point cloud의 sparse한 영역의 한점에서 나온 line이 dense한 영역을 통과하는 경우를 가정. 논문서 제안한 방법을 사용하면, peak finding의 결과가 dense한 영역에 나타날 것이므로, sparse했던 original 위치와 다른 문제가 발생한다.

5. Experimental Results

• Indoor & Outdoor scenes에 대해서 line clouds를 point clouds로 복원
• Recover된 point cloud를 이용하여 InvSfM을 사용하면 어느정도까지 이미지 content가 복원되는지 확인
• 매우 sparse한 line clouds로부터 복원된 결과이미지가 사람이 알아볼 수 없다는 것을 보임

결론적으로, point cloud를 lifting하는 것만으로는 privacy-preserving이 충분치 않다는 것을 보임

Dataset

• Cambridge Landmarks & 12 Scenes dataset을 사용

Recovering point clouds

위의 그림은, 위에서부터 순서대로 SfM을 통해 얻은 Original Point cloud와 이를 lifting하여 얻은 line clouds, 논문서 제안한 방법을 통해 line clouds로부터 복원한 point clouds를 가리킨다.

• Higher point density일수록 detail있게 복원됨
• 이웃한 점들간의 거리가 짧을수록, 정확히 point position을 찾을 수 있음

정량적인 지표 (원래 point들과 복원된 points간의 유클리디언 거리)도 제시함

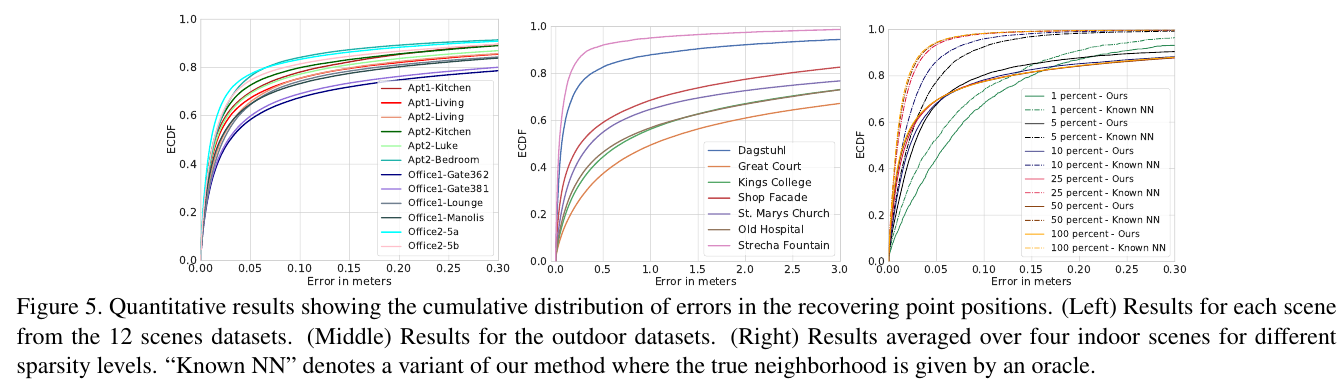
• 실내가 실외보다 에러가 적다. 이는 앞에서도 언급했듯이, estiamted neighbors간의 거리에 따라 accuracy가 결정된다는 것을 보여준다.

Recovering image details

line clouds로부터 복원한 point clouds를 pretrained된 InvSfM에 넣은 결과는 아래와 같다.

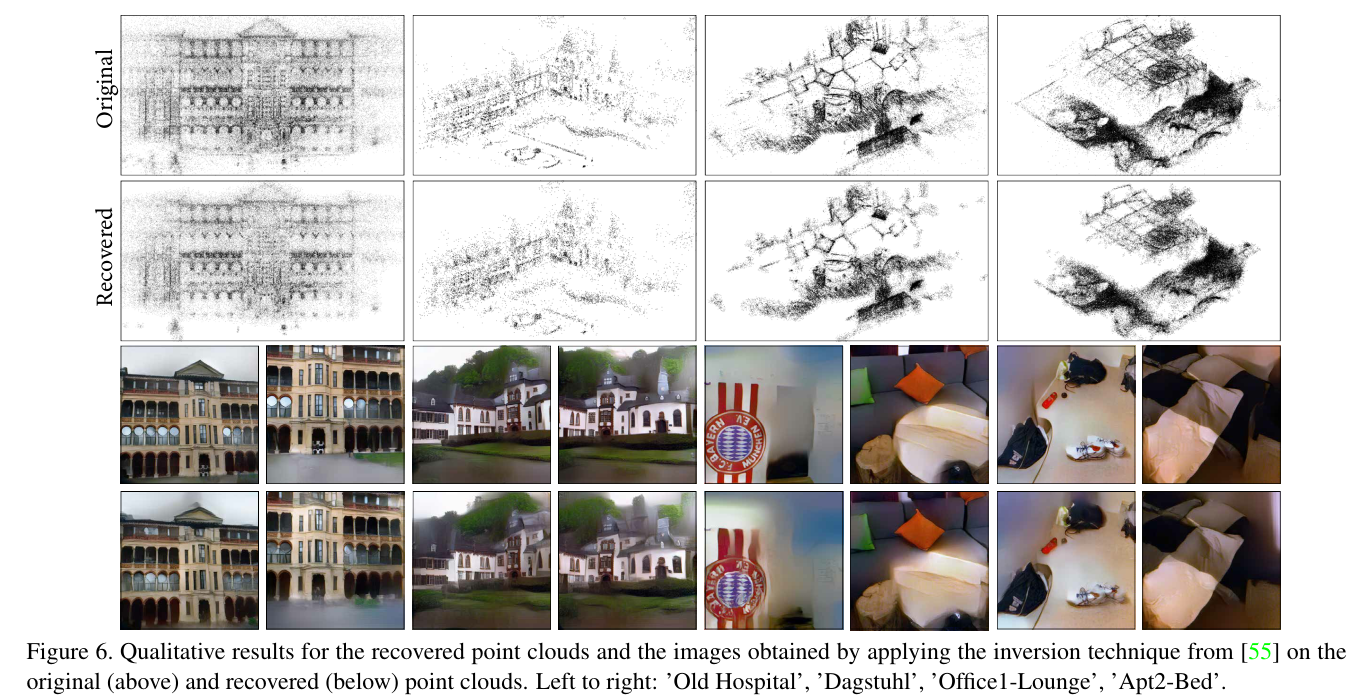
• Noisy한 point clouds일수록 blurry하거나 wavy line들이 나타난다
• 하지만 건물의 전반적인 형태, 문의 shape등을 보면 detail이 잘 복원된 것을 알 수 있다

저자들은 point clouds를 단순히 lifting하는 것만으로는 privacy-preserving이 충분하지 않다고 한다.

Sparse line clouds prevents image recovery

• Sparser한 line clouds를 사용하더라도 accurate localization이 가능하며, 정확한 point clouds를 recovery하는 것이 불가능하다

• 실제 original의 5%만 사용하여도 복원이 가능하다

• 하지만 위의 경우처럼, 10% 이하부터는 image의 detail이 떨어지는 것이 관찰됨.

6. Conclusion

• Line clouds를 point clouds로 복원하는 방법을 제안

• point clouds를 lifting하는 것만으로는 privcay-preserving에 충분치 않다

• Sparsity가 결국 privacy preserving에 핵심이라고 할 수 있다

Reference

• https://www.youtube.com/watch?v=PdwGHHizKXM (저자 youtube영상)
• InvSfM 논문: Revealing Scenes by Inverting Structure From Motion Reconstructions, CVPR, 2019
• Lifting point clouds 논문: Privacy Preserving Image-Based Localization, CVPR, 2019