본 논문은 고전적인? 논문이라 할 수 있지만, 6개의 점을 이용하여 2개의 generalized 카메라의 relative한 pose를 구하는 방법을 제시한 논문이라 할 수 있음.

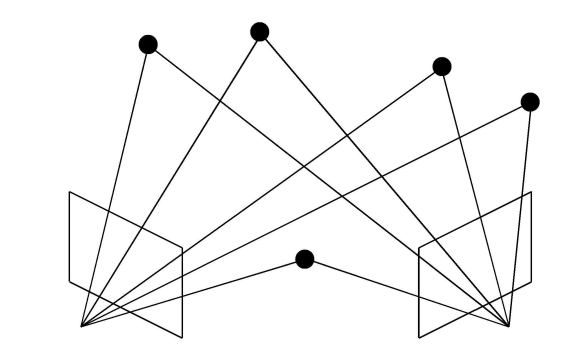
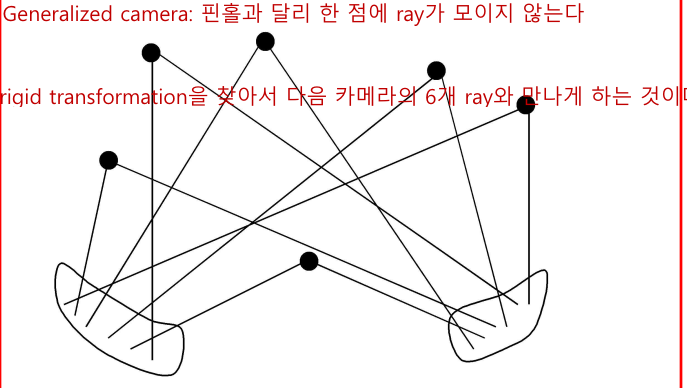
• Generalized camera: 핀홀카메라와 달리 ray가 중심으로 모이지는 않는 모델. 아래 그림처럼 ray가 모이지 않는다.

• 만약 카메라가 calibrate 되었다고 하면, ray를 얻을 수 있고, 하나의 카메라의 6개의 ray를 변환하는 rigid-body transformation을 구하면 된다. 처음 카메라의 6개 ray들이 변환되어 다음 카메라의 6개의 ray와 만나야 한다는 것.

• 위 문제는 64개의 일반해를 가지고 있으며, 64x64 행렬로 만들어 eigenvector를 추출하는 방식으로 문제를 해결한다고 함

• RANSAC과도 같이 사용할 수 있다고 함

1. Introduction

• Calibrated perspective camera(ex. pinhole)의 경우는 2개의 카메라에서 나온 5개의 ray들의 교점을 알면 상대적인 pose를 구할 수 있음. 아래 그림.
  
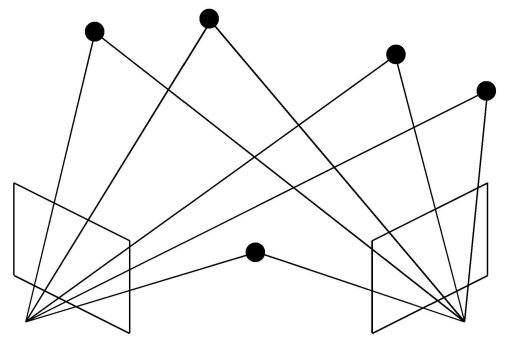
• Generalized camera들이 많이 등장함. 본 논문에서는 generalized camera problems에 대해 6개로 카테고리화 하고, 이에 대한 slover를 제시

2. Generalized Camera Model

• 플루커 벡터 표현을 이용하여 선에 있는 모든 점들을 쉽게 표현할 수 있다
• Generalized Camera Model에 대한 자세한 설명은 https://velog.io/@wilko97/3D-Computer-Vision-Lecture-12-part1-Generalized-Cameras 참고.

3. Minimal Cases

• Generalized cameras의 Pose와 상대적 pose를 구하는 최소해의 경우를 카테고리화 시켰다.

Relative Pose with a Euclidean Generalized Camera

• 각 카메라는 6자유도를 가짐,
• m개의 카메라와 n개의 rays이 각 이미지에서 관찰되었다고 하면, 총 $2mn-3n-6m+6$개의 제약조건이 도출된다고 함(이유는 정확히 모르겠음)
  
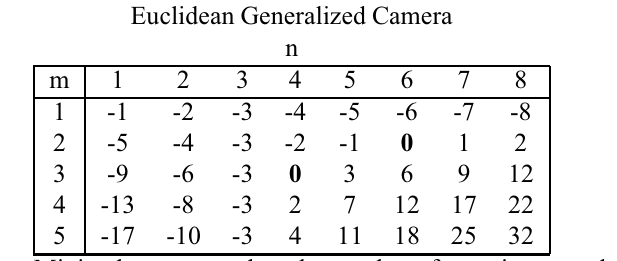
• 아래와 같이 최소해인 경우, m=2, n=3일떄 총 64개의 해를 얻을 수 있음

Relative Pose with a Affine Generalized Camera

• Affine Generalized camera의 경우 카메라의 포즈가 affine 행렬변환으로 나타난다는 것임
• 총 $2mn-3n-12m+12$개의 제약조건이 도출된다고 함
  
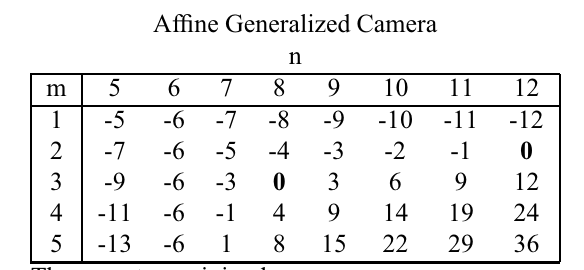
• m=2, n=12일때 348개의 solution이 도출됨

Generalized Pose

• affine generalize camera의 경우 general case의 특수해인 경우임