• 「 DeepFool: a simple and accurate method to fool deep neural networks」, CVPR, 2016 - Seyed-Mohsen Moosavi-Dezfooli, Omar Fawzi, Pascal Frossard

Abstract

최신의 deep neural network는 image classification에서 놀라운 성취도를 달성하고 있습니다.
그러나 이 아키텍쳐들은 small, well sought한 pertubation에 무척 취약합니다. 이러한 현상에도 불구하고, 아직까지 딥러닝 모델들의 robustness를 측정하는 effective한 방법은 제안되지 않았으며, 이 논문은 DeepFool 알고리즘의 제시를 통하여, perturbation을 계산하는 방법과 모델들의 roubustness를 수량화하는 효율적인 방법을 소개하고자 하려합니다.
첨부된 실험 결과에 따르면, 이 논문서 제시하는 접근방법이 기존의 perturbations들을 계산하는 방법보다 뛰어나며, classifier들을 더욱더 robust하게 만들수 있다고 합니다.

1. Introduction

실제로 많은 딥러닝 모델들이 매우 작고, 육안으로 인지불가한 perturbations에 의해 incorrect한 classification을 한다고 합니다.

아래 그림은 perturbations의 예시인데요, 첫번째 사진은 original image의 고래이며, 두번째 그림은 DeepFool에 의해 '거북이'로 오분류 된 이미지이며, 마지막은 FGSM에 의해 perturbated된 이미지입니다. DeepFool 방식은 FGSM에 비해 small한 perturbation을 가지는 것을 확인할 수 있습니다.

이 논문에서는 label을 오분류 시킬수 있는 최소한의 perturbation r을 다음과 같이 정의합니다.

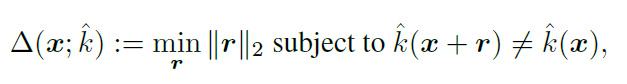
• x : original image
• r : miminal perturbation
  △(x; k)는 point x에서의 classifer k의 robustness를 의미하며, 전체 classifier k의 robustness는 아래와 같이 정의할 수 있습니다.

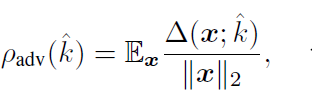
• E(x) : expectation over the distribution of data.

Adversarial perturbations에 대한 조사는 classifier가 어떠한 features들을 사용하고 있는지 이해하는 데 도움을 준다고 합니다. 또한 adversarial attack은 across model, 즉 모델에 상관없이 generalization이 가능하다고 합니다.

이 논문의 Contribution은 다음과 같다고 합니다

• Simple하고, accurate한 방법의 제안과, 여러개의 classifier의 adversarial perturbations에 대한 robustness 비교
• 기존의 adversarial 방법들보다 reliable, effiecient한 방법의 제시와 training data에 adversarial examples을 같이 주었을 때의 roubustness의 향상
• 흥미로운 adversarial perturbations에 대한 이해와 영향 요소들에 대한 이해

「In International Conference on Learning Representations (ICLR), 2014」 논문에서 처음으로 adversarial instability의 개념이 제시되었다고 합니다. 위 논문에서는 penalized optimization 문제의 해결과 신경망은 높은 complexity에 대한 분석으로 adversarial examples의 존재를 설명하려 하였습니다. 하지만 이 방법에서 사용된 최적화 방법은 time-consuming하며, large dataset에 scale되지 않는다는 단점이 있었습니다.

이후로 많은 논문들에서 adversarial examples에 대한 존재의 이유를 설명하려 했으며,
「Explaining and harnessing adversarial examples(ICLR), 2015.」논문에서 FGSM방법이 제안되었습니다. 하지만 이 방법은 optimal perturbation vector를 구하는 대략적인 근사 방법이었습니다.

이러한 perturbation에 대한 공격을 막기 위해, 「Towards deep neural network architectures robust to adversarial examples」에서는 training에 smooth한 penalty를 주어 robust한 classifier를 만드는 방법을 소개하기도 합니다.

이러한 adversarial에 대한 이해는, classifier에 대한 깊은 이해를 바탕으로 한다고 합니다.
이 논문서 제안하는 method는 효울적이고 정확한 adversarial perturbation을 만드는 것의 baseline이 될 것이라고 합니다.

2. DeepFool for binary classifiers

이 섹션에서는 binary classifier에 대한 perturbations을 구하는 efficient한 알고리즘을 제시하고 있습니다. 먼저 scalar-valued 방식의 임의의 이미지 분류 함수 f에 대해 다음과 같이 가정합니다.
ˆk(x) = sign(f(x))
이후에 f가 아래와 같이 affine classifier인 경우부터 분석하여, general algorithm을 얻어냅니다.

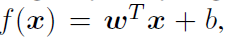
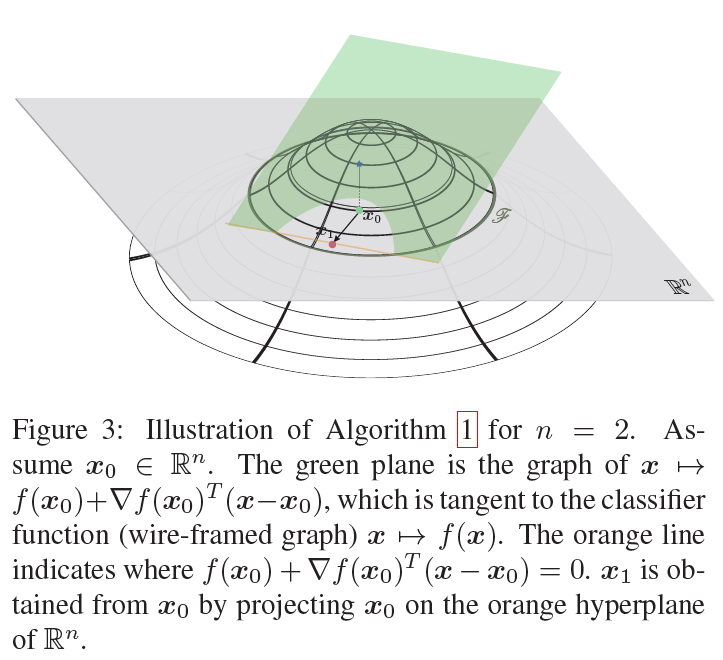
f가 affine 변환인 경우, x0에서의 robustness를 쉽게 구할 수 있습니다

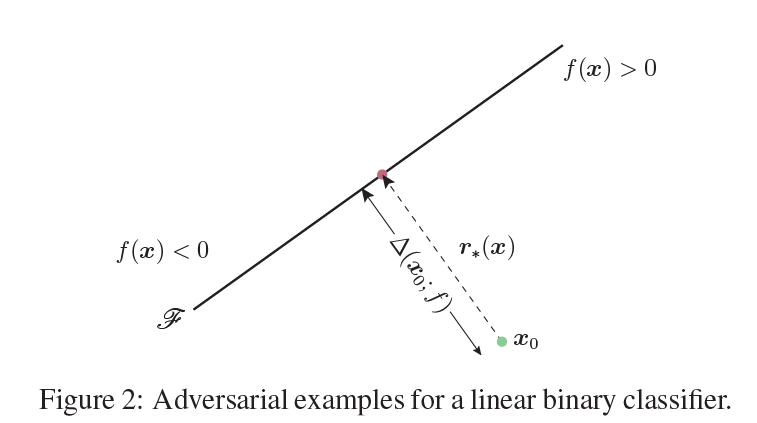
△(x0; f), robustness는 초평면 F와 x0사이의 거리와 같습니다.
minimal perturbation은 x0에서 F에 정사영된 점이라 할 수 있습니다.
x0를 F에 projection하여, minimal perturbation 벡터를 구하는 방법을 공식화하면 아래와 같습니다.

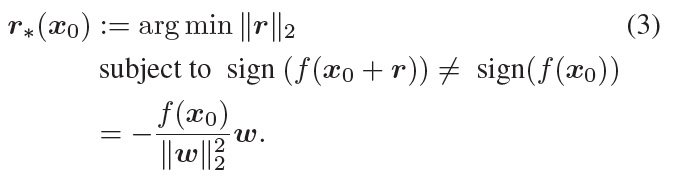
f를 일반적인 binary classifier라 가정했을 때, robustness △(x0; f)를 측정하기 위해 iterative한 method를 사용한다고 합니다. 각 iteration마다 minimal perturbation(r(i))은 아래와 같이 구합니다

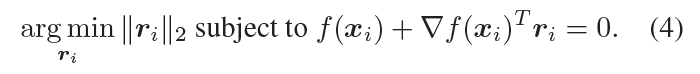
위에서 구한 minimal perturbation, r(i)를 가지고 x(i+1)를 update하며, x(i+1)가 classifier의 sign을 change할 때, 멈추게 됩니다.

아래 그림은 위의 알고리즘에 대한 예시를 나타낸 그림입니다.

3. DeepFool for multiclass classifier

이 섹션에서는 binary classifier에 대한 개념을 확장 시켜서 multiclass에 대해서 적용하는 방법을 소개합니다. multiclass classifier에서 가장 많이 사용하는 방식은 one vs all방식인데요, classifier가 c개의 output을 가진다고 했을 때, f(R(n) -> R(c))에 대해서 다음과 같이 mapping 될 수 있음을 알 수 있습니다.

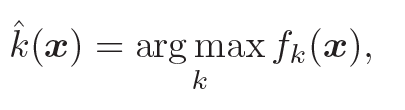
• fk(x) : classifier의 output f(x)이 kth class에 속하는 것

3.1 Affine multiclass classifier

f(x)를 affine classifier라 두겠습니다. f(x) = W⊤x + b. kth에 mapping하는 one vs all의 스키마를 이용하면, minimal perturbation, r은 다음과 같습니다

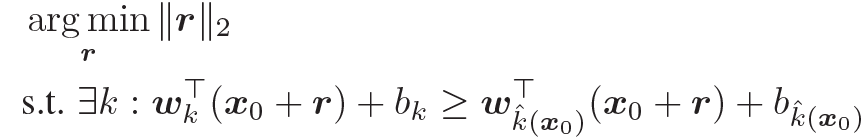
• w k : kth column of W

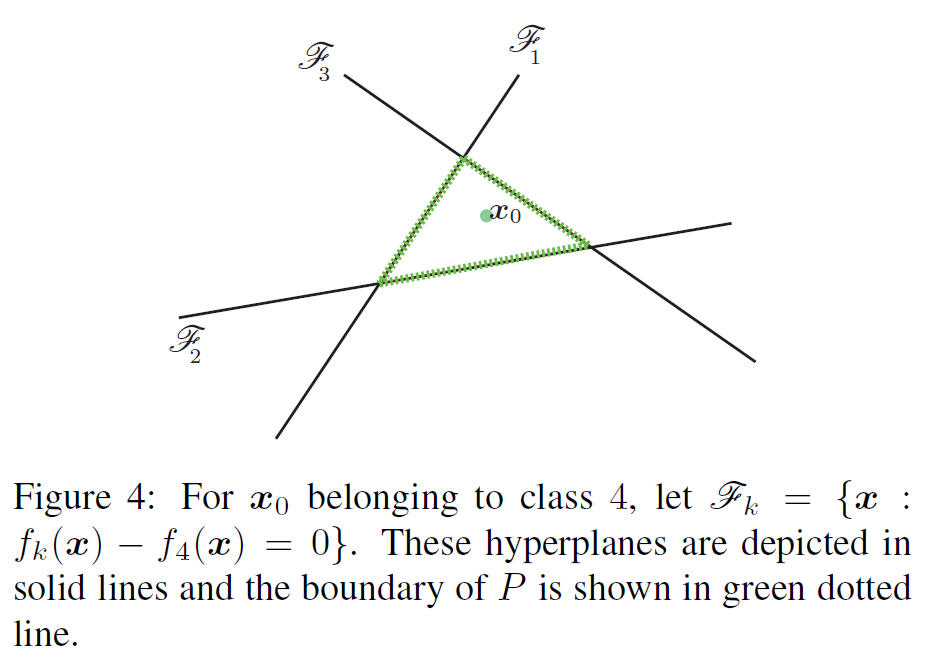
기하학적으로, ||r||을 구하는 것은 결국 점 x0와 그림(Figure 4)처럼 x0를 둘러싼 convex한 (green line으로 둘러싼) 다면체 P와의 거리를 계산하는 것이라고 합니다. 다면체 P는 다음과 같이 정의할 수 있습니다.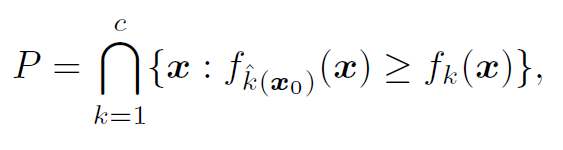
점 x0는 P안에 있으며, x0와 다면체 사이의 거리를 dist(x0, Pc)로 denote하고 있습니다.
ˆl (x0)는 가장 가까운 평면과의 거리라 정의하면은(Figure 4에서는 F3와의 거리), ^l(x0)를 구하는 공식은 아래와 같습니다

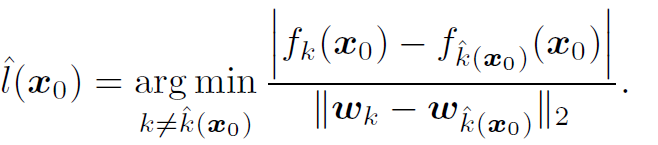
minimum perturbation r*(x0) 벡터는 ^l(x0)에 의해 index된 초평면에(Figure 4의 경우 F3) x0를 project한 것과 같습니다. 즉, 점 x0에서 P로 projection 했을 때, closest한 것을 찾는 것이라 합니다.

3.2 General classifier

이 part는 affine classifier가 아닌 general case에 대해 확장하여 적용하는 것을 설명합니다.

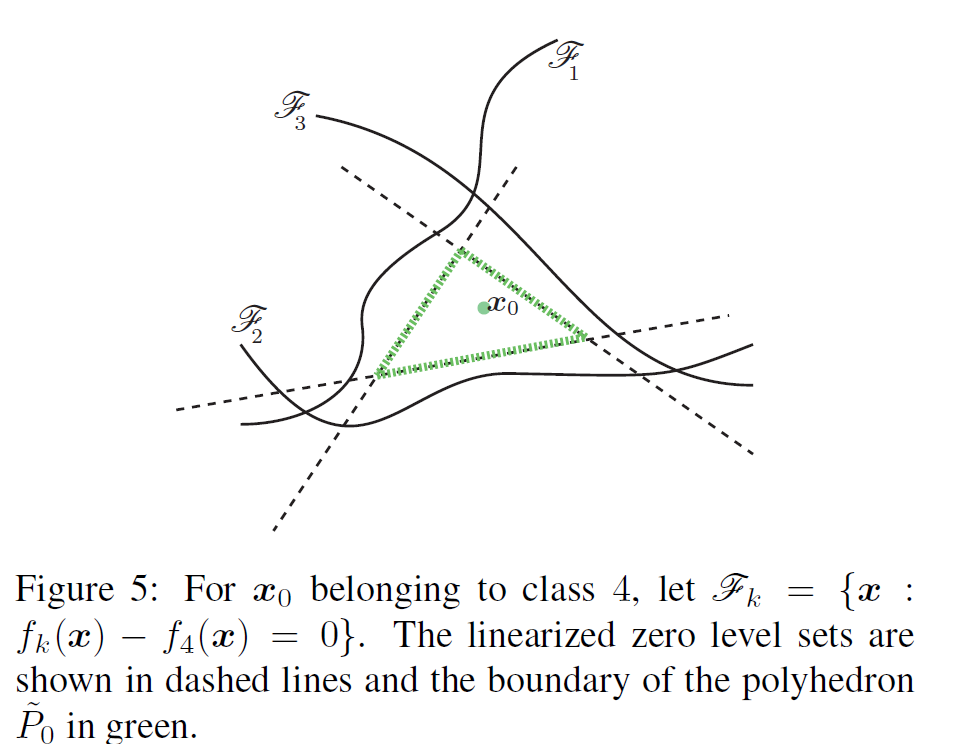
일반적인 non-linear한 classifier에 대해서, set P는 위의 그림처럼 더이상 다면체가 아닌 형태가 됩니다.
binary classification case에서 봤던 iterative method를 이용하여 iteration i번째서의 새로운 P(i)를 다음과 아래와 같이 정의할 수 있습니다.

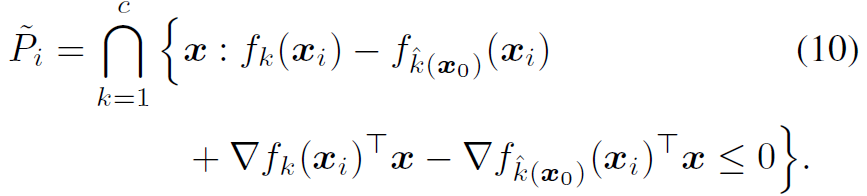
dist(x(i), P(i)c)는 dist(x(i), ˜P(i)c)의 근사화를 통해 계산할 수 있다고 합니다.
즉, iterative한 각각의 경우에서, non-linear한 decision boundary를 linear approximation을 통해서 가장 가까운 방향을 찾는 것이라 할 수 있겠습니다. 위의 내용은 아래의 algorithm2에 구현되어 있습니다.

위와 같이 제안된 방법은 greedy alogrithm이고 optimal한 perturbation에 도달하지 않지만, 충분히 좋은 approximation을 보여주고 있다고 합니다.

3.3 Extension to ℓp norm

지금까지 논문에서는 ℓ2 norm을 이용하여 perturbation을 측정하였습니다. 하지만, 이를 넘어서 ℓp norm에도 적용할 수 있는 방법을 아래와 같이 제시하고 있습니다. 이를 위해서는 알고리즘2의 10,11번째 줄, update step하는 부분을 다음과 같이 바꾸면 된다고 합니다.

특히 p = ∞일때는 다음과 같다고 합니다

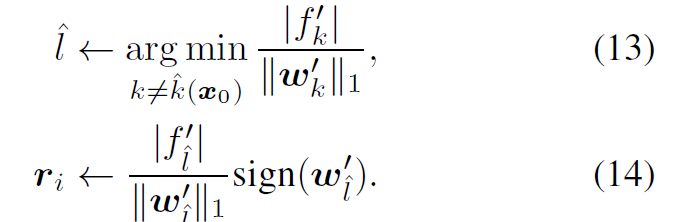
4. Experimental results

이 섹션은 이제 다양한 아키텍쳐에 DeepFool 방식으로 perturbation을 주었을 때의 결과를 보여주고 있습니다.

4.1 Setup

위 실험은 MNIST, CIFAR-10, ILSVRC 2012 3가지 dataset을 사용하였습니다.
adversarial perturbation의 average robustness는 아래의 공식을 이용하여 evaluate하였다고 합니다.

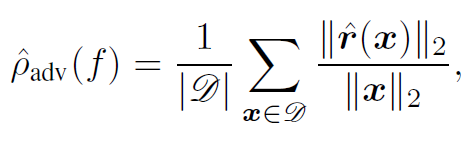
• r(x) : DeepFool을 통해 얻은 minimal perturbation
• D : test set

이 평가지표를 사용하여 DeepFool 방식과 FGSM(ρadv [4]로 명명),「Intriguing properties of neural networks. In International Conference on Learning Representations (ICLR), 2014.」에 구현된(ρadv [18]로 명명) series of penalized-optimzation problem을 풀어 minimal perturbation을 구하는 방법과 비교하였다고 합니다.

4.2 Result

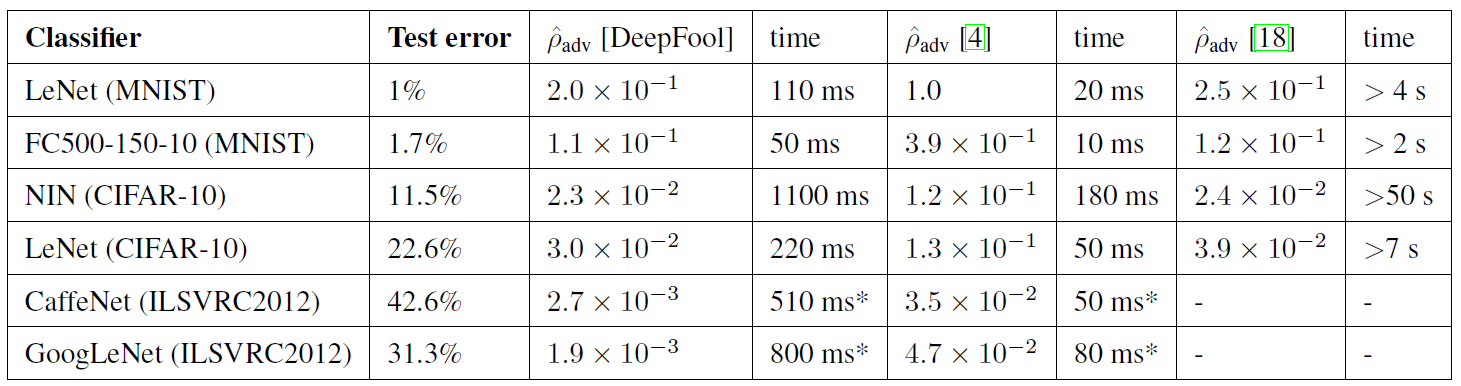
DeepFool을 활용한 방식의 robustness가 기존의 방식들보다 작은 것을 확인 가능합니다. 복잡성 측면에서도, ρadv [18]보다 빠르게 되었다는 것을 확인할 수 있었습니다.
DeepFool은 다른 adversarial attack 방법들보다 보다 더 작은 perturbation을 만들어 낸다고 합니다.(블로그 맨 처음 그림 참조) ℓ∞norm을 사용해도 결과는 유지된다고 하고 있으며, 아래의 표는 P∞adv(f) 값에 대한 결과입니다.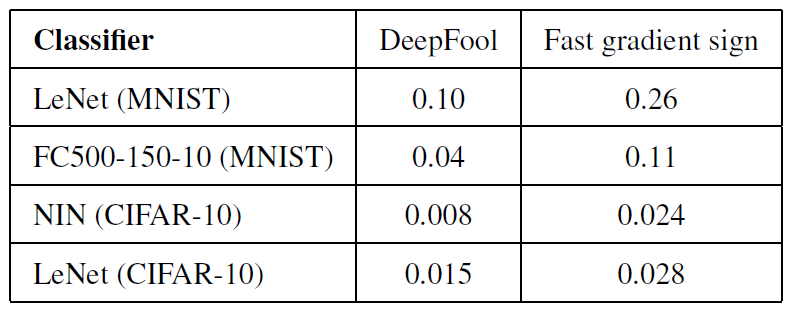
두 방법 모두 다 90%이상의 오분류를 하였다고 합니다

4.3 Fine-tuning using adversarial examples

이 섹션에서는, 위의 표에서 제시되었던 network들을 adversarial examples에 대해 fine-tune시켜서, robust한 MNIST, Cifar-10 classifier를 구축합니다. DeepFool adversarial examples과 FGSM adversarial examples에 대한 fine-tune을 각각 진행합니다. Fine-tune의 과정은 perturbated된 training set에 대해서 5epoch의 추가적인 training을 진행하였다고 합니다.

아래의 그래프들을 Fine-tune 이후에 robustenss의 결과를 제시한 것입니다.

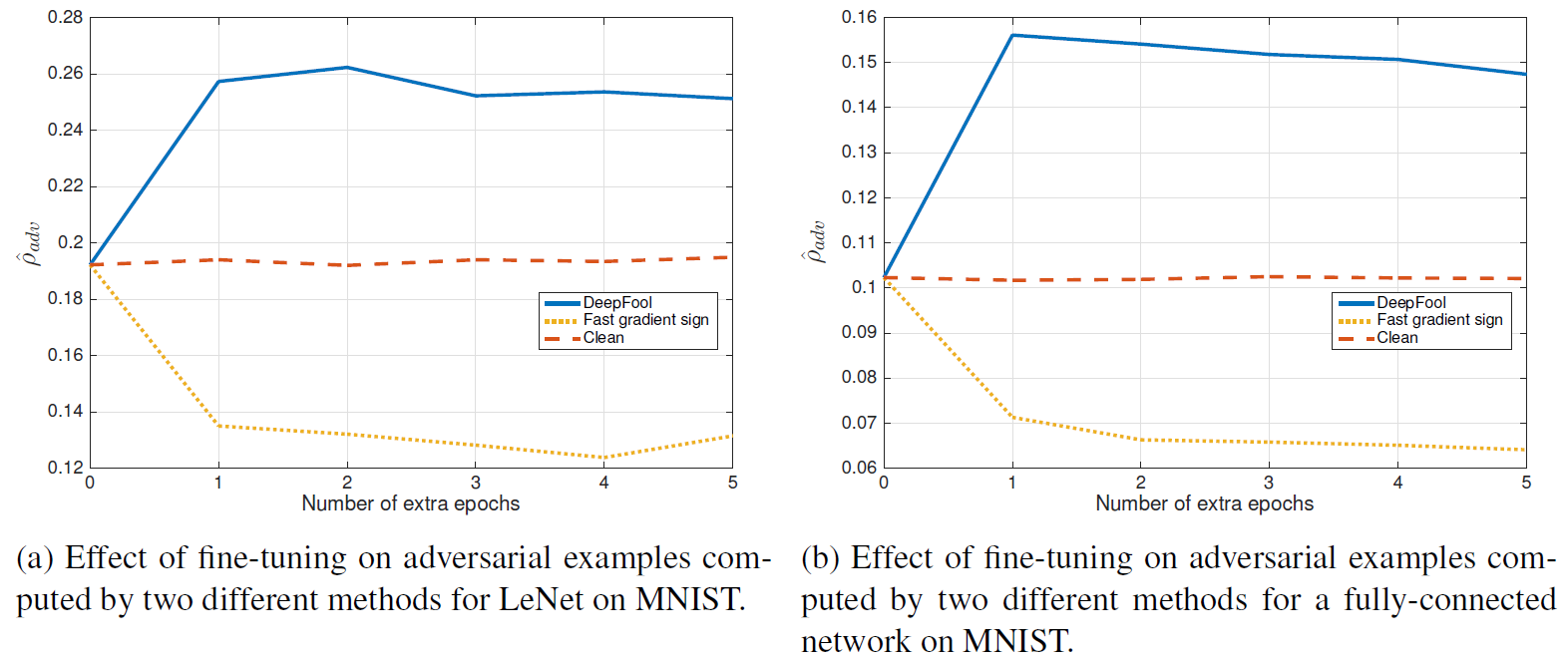
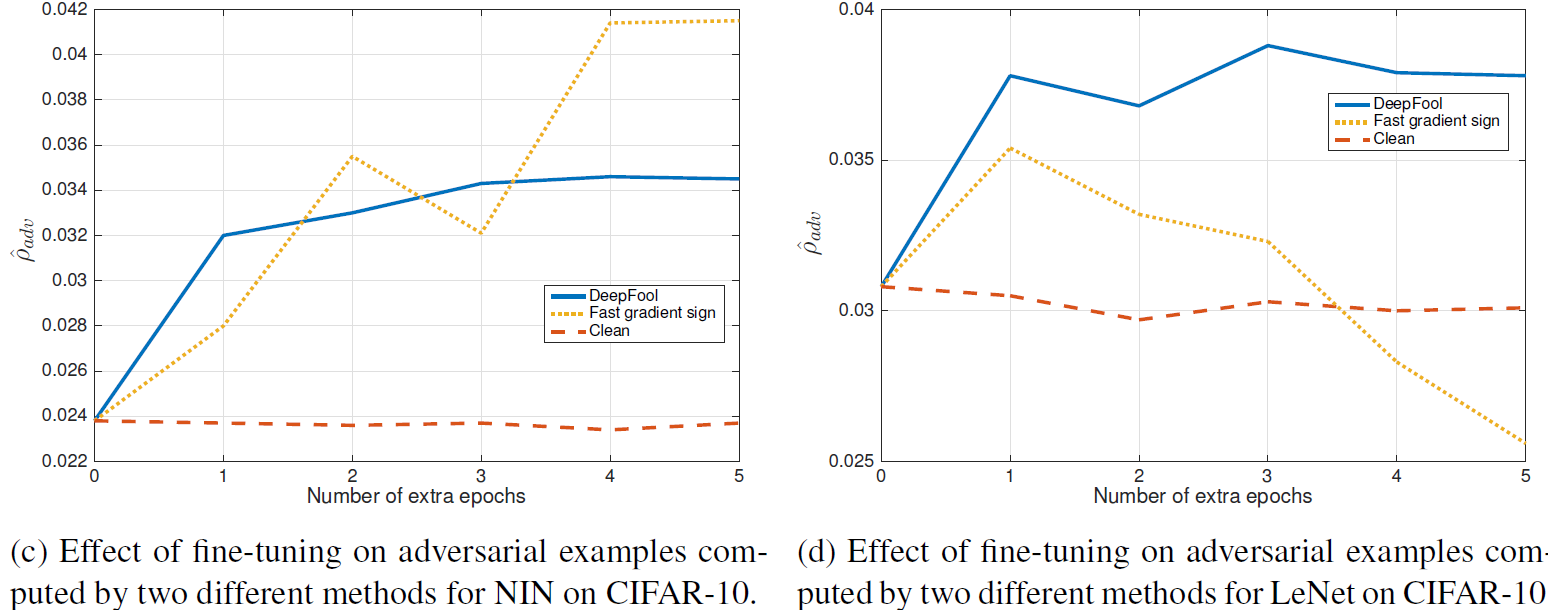
위의 결과들을 살펴볼때, DeepFool을 이용한 perturbated training set을 1epoch만 훈련시켜도 robustness의 significant한 향상이 보인다고 합니다. 반면에, FGSM 방식을 이용했을 때, robustness가 오히려 감소하는 경우도 있는데, 이는 FGSM의 perturbation이 minimal perturbation보다 크기 때문이라는 가설을 제시하고 있습니다. 즉, overly 하게 perturbated된 이미지를 훈련시키면 오히려 robustness가 감소한다는 것입니다. 이 가설을 증명하기 위해, DeepFool 방식을 이용한 perturbation의 norm을 multiple(α = 1, 2, 3)하여, robustness를 측정한 결과를 제시하고 있습니다

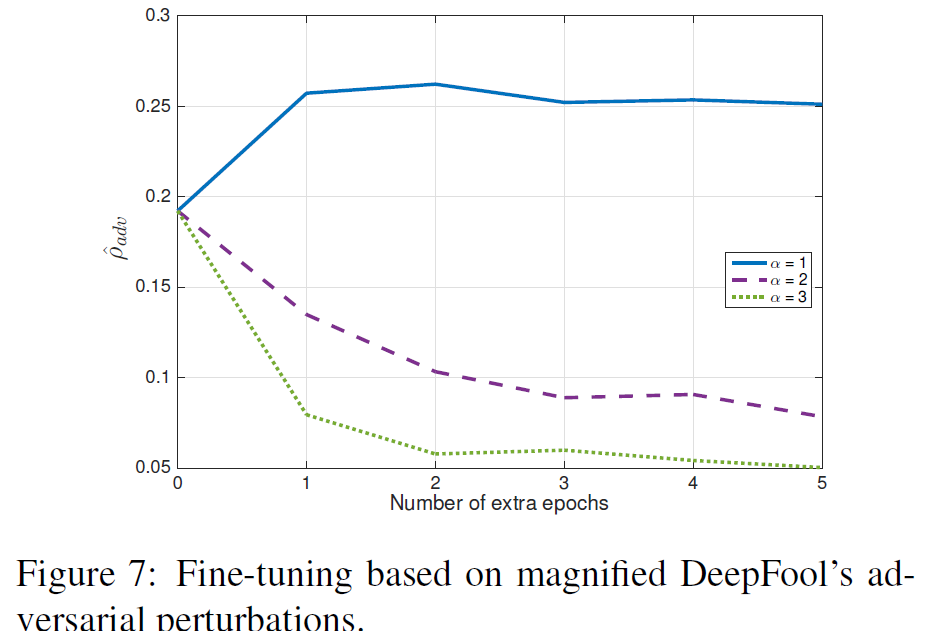
MNIST에서 이렇게 과도하게 perturbated된 이미지들은, 아래 그림처럼 실제로 숫자를 바꾸는 결과를 초래하게 되어서, 아예 다른 class가 되어, robustness가 낮아진다고 합니다.

아래의 Table3은 fine-tuned된 network들의 accuracy를 나타낸 것입니다. DeepFool방식은 accuracy가 imporve되었지만, FGSM방식은 오히려 decrease 되었습니다. 논문에서는 이 결과가, FGSM 방법이 결국에 overly perturbated된 images들을 만들어 낸다고 합니다. 마치, orginal data distribution을 represent하지 않는 regularizer처럼 된다고 합니다.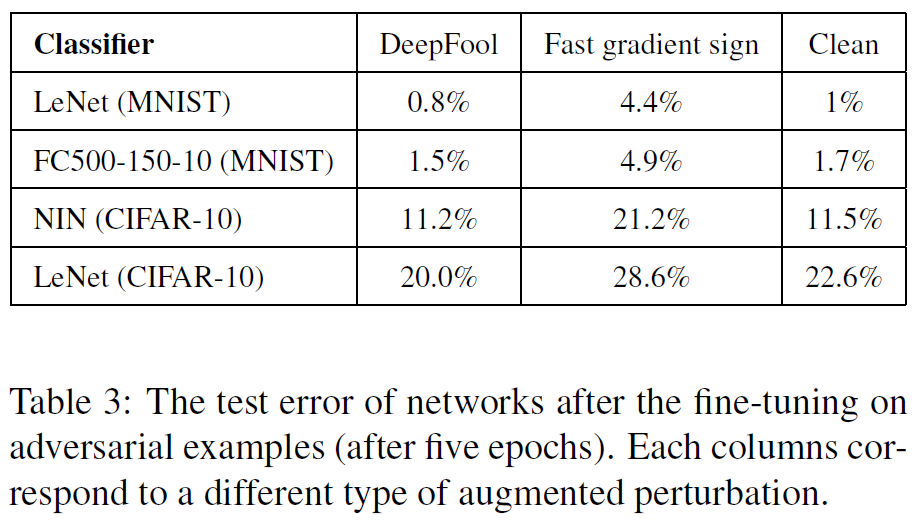

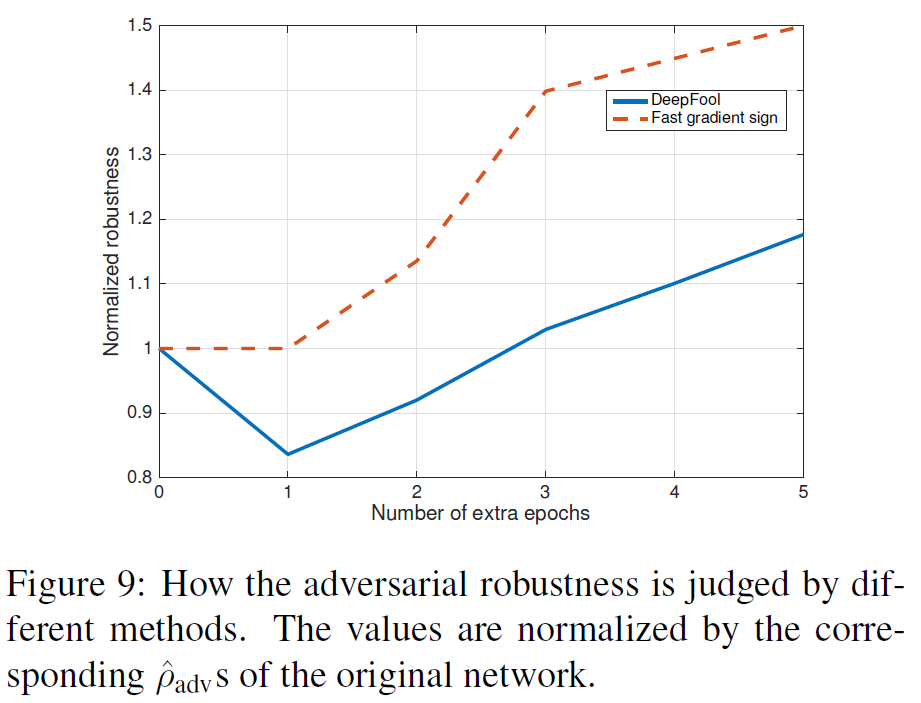
마지막으로 correct estimation of the minimal perturbation에 관한 설명이 나옵니다. 아래 그래프(Figure 9)는, FGSM 방식으로 NIN classifier를 fine-tune한 이후에, 앞선 방식에 비해 learning rate을 90% 감소시킨후, DeepFool과 FGSM을 각각 사용한 extra epochs를 이용하여 evaluate한 결과입니다. DeepFool보다 FGSM의 robustness가 더 좋은 것을 확인 가능하며, DeepFool의 1번째 epoch는 오히려 robustness가 감소하는 것을 볼 수 있습니다. 이러한 결과는 결국에 accurate한 tool을 사용하여 robustness를 평가하는 것이 매우 중요하다는 것을 보여준다고 합니다

5. Conclusion

DeepFool이라는 새로운 adversarial algorithm을 소개하였습니다. 이 방법은 iterative linearization을 바탕으로 classifier의 label을 바꾸도록 minimal한 perturbation을 구하는 방식입니다. 실험결과를 통해 DeepFool 방식의 유효성을 보였으며, 제안한 방법이 classifier의 robustness를 정확하고 효율적으로 계산 가능하며, fine-tune을 통한 robustness 향상에 기여했다고 합니다.

감사합니다.^^