- 「Universal adversarial Perturbations」, CVPR, 2017 - Seyed-Mohsen Moosavi-Dezfooli, Omar Fawzi, Alhussein Fawzi, Pascal Frossard
Abstract
이 논문은 Universal(이미지에 적용되는)하고 매우 작은 Perturbation vector의 존재에 대해 입증하고 있습니다. Perturbation을 원본 이미지에 더하면 DNN classifier가 예상과 전혀 다른 output을 출력하게 됩니다. 또한 이 논문에서는 Universal한 Perturbation을 구하는 알고리즘을 제시하였고, 딥러닝 모델들이 이에 대해 매우 취약하다는 사실을 입증하였습니다. 이러한 universal perturbation의 존재는 고차원의 classifier의 decision-boundary에서의 기하학적인 상관관계를 보여주고 있었습니다. Perturbation vector는 대부분의 image classifier을 break할 수 있다고 합니다.
1. Introduction
이 논문에서는 universal perturbation vector의 존재성을 입증하였고, 이 벡터는 natural image들을 높은 확률로 misclassify하게 만듭니다.
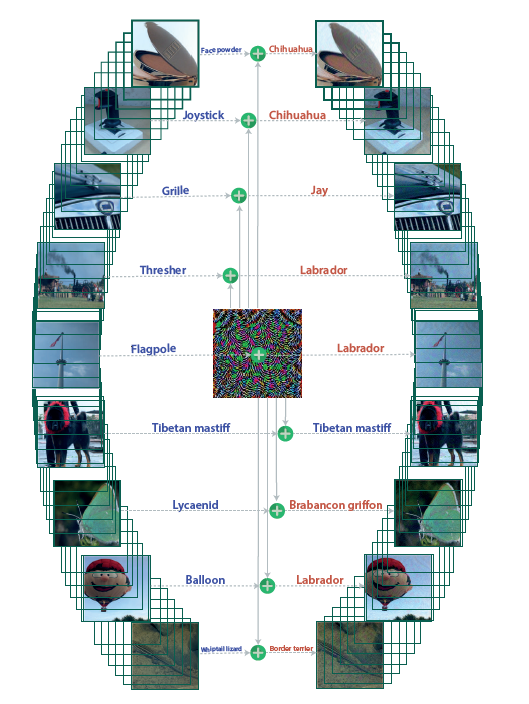
위의 그림은 실제로 Universal perturbation을 주었을 때, original 정답(왼쪽)과 딥러닝 classifier의 분류 결과를 보여주고 있습니다(오른쪽). 성능이 매우 안좋은 것을 확인할 수 있었습니다.
이러한 attack들은 실제로 보안적인 측면에서 상당히 중요한 이슈가 되고 있으며, perturbation이 추가된 이미지들은 육안으로 구별하기 힘들지만, data distribution에 상당한 영향을 끼쳐 모델을 break합니다
아래는 이 논문에서 다룰 내용에 대한 요약입니다.
- Image-agnostic(범이미지적)인 Deep-neural network에 대한 universal perturbation의 입증
- Universal perturbation을 구하는 알고리즘 제시
- Universal perturbation의 놀라운 일반화 능력에 대한 입증
- Across Images뿐만이 아니라, across deep neural network(doubly universal)까지 generalization이 가능하다는 사실
- 서로 다른 decision-boundary들의 기하학적인 상관관계에 대한 탐구를 통한 딥러닝 모델들의 Universal perturbation에 대한 높은 취약성 설명
기존의 Adversarial perturbation의 가장 기본적인 특징은 datapoints들에 대한 intrinsic dependence 였습니다. 이러한 방법들은 각각의 모든 datapoints에 대해 specially craft하는 과정이 필요하며, data-dependent한 optimization problem을 해결해야 하며, model에 대한 완전한 사전 지식을 알고 있어야 합니다.
하지만 이 논문에서 제시한 Universal perturbation은 단 하나의 single perturbation vector를 찾아, datapoint에 더해주면 되는 것입니다. 또한 optimization problem이나 gradient 계산 역시 필요 없으므로, 훨씬 더 효율적인 방법이라고 생각됩니다.
2. Universal perturbations
이 섹션에서는 Universal perturbation의 개념 소개와 방법을 제시하고 있었습니다
μ를 d차원 이미지들의 분포라고 하고, ^k를 classifcation function이라 할 때, clean 이미지 x에 대해 estimated된 label을 ^k(x), perturbation vector를 x에 주었을 때 분류된 label은 ^k(x+v)라 할 수 있습니다. Perturbation vector v는 아래의 식을 만족하는 벡터를 찾으면 될 것입니다.
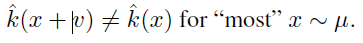또한 data distribution(μ)에 따라 label이 변하므로, variability가 높다고 할 수 있습니다. 이러한 내용을 바탕으로 아래의 두 제약조건을 만족하는 v를 찾습니다.
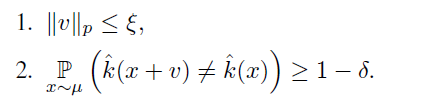
입실론(ξ)은 perturbation vector v의 크기를 조정하며, δ는 desired fooling rate를 나타냅니다.
Algorithm
X = {x1, . . . , xm}를 image distribution μ로부터 샘플링된 이미지들의 집합이라 둡니다. ξ값보다 크기는 작으면서 X에 있는 이미지들을 fooling할 수 있어야하는 v벡터를 찾는거이 주된 목표가 됩니다.
이 알고리즘은 iterative한 approach를 사용합니다. X의 원소에 대해 iterative하게 진행된 이후, 최종적으로 Universal perturbation을 얻게 됩니다. 각 iteration에서는 현재의 data point(x(i))를 decision boundary 밖으로 보내는 minimal perturbation △v(i)를 구하고, △v(i)를 더하여 최종적으로 perturbation vector v를 구하게 됩니다. 아래의 식은 이 방법을 formulize한 것입니다
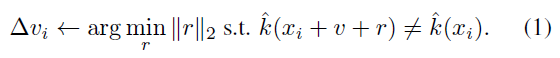
이제 벡터의 크기가 ξ보다 작다는 제약조건을 보장하기 위해서, updated된 Universal perturbation은 원점을 중심으로 반지름이 ξ인 구에 projected(정사영)됩니다. 아래는 이 project operation을 나타낸 것입니다
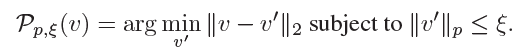
이 논문에서는 최종적으로 perturbation vector를 update할 때, 아래와 같이 각각의 data-point에 대한 minimal perturbation 벡터를 구하고, 이것을 project한 것을 update하는 방법을 사용하였습니다.
이러한 iteratvie한 알고리즘은 fooling rate가 target threshold인 (1-δ)값을 넘게 되면 중단됩니다
이는 아래와 같이 표현될 수 있습니다
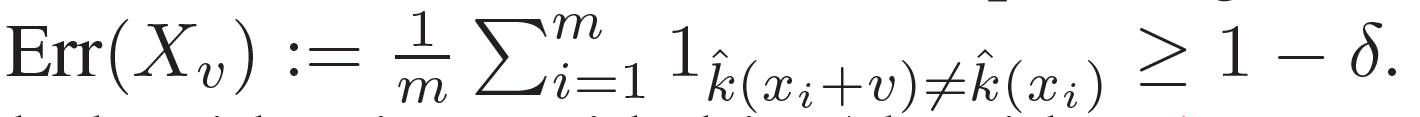
논문에서 소개한 이 알고리즘의 흥미로운 점으로는, X속에 있는 적은 수의 data points를 가지고도 전체 distribution에 적용되는 Universal perturbation을 만들 수 있다는 점입니다.
위의 아이디어를 종합하여 정리한 알고리즘은 아래와 같습니다.
위 알고리즘은 distribution으로 부터 샘플링된 data points들을 속이는 smallest한 Universal perturbation을 찾는 것이 아니라, small norm을 가지고 하나의 perturbation을 찾는 것이라 할 수 있겠습니다. 또한 X를 shuffling함에 따라서, 다양한 universal perturbations v를 얻을 수 있습니다.
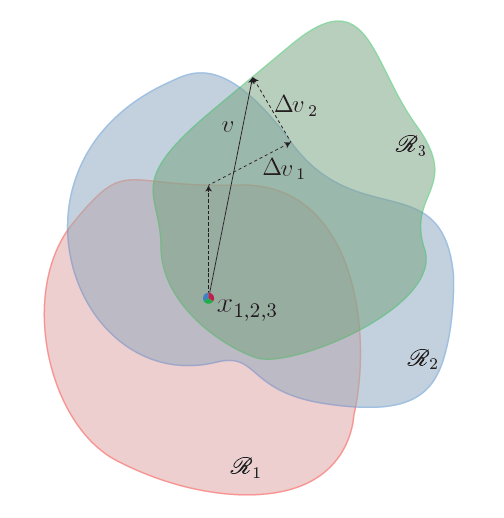
다음 그림은 알고리즘의 원리를 시각화 한 것입니다. x1, x2, x3는 data points들이며, R(i)는 classification region을 나타낸 것입니다. 이 논문에서 제시한 바와 같이, minimal perturbation을 더하면서 v를 구하여, perturbated points(x(i) + v)을 classification region(R(i)) 밖으로 밀어내는 것을 확인할 수 있습니다.
3. Universal perturbations for deep nets
이 섹션에서는 Universal perturbation을 사용하여, 이 당시 최근 딥러닝 모델들의 robustness를 평가하고 있었습니다. Result는 다음과 같다고 합니다.
set X는 perturbation 계산을 위해 사용된 data이며, Val은 계산에 사용되지 않은 데이터입니다.
결과를 보면 universal perturbation 방식은 매우 높은 fooling rate를 달성하였습니다
CaffeNet과 VGG-F는 validation에 대해 90%이상 속았습니다. 이 결과는 이 방식이 특정 아키텍쳐에만 적용되는 것이 아니라, 많은 아키텍쳐에 적용 가능하다는 것을 보여주고 있다고 합니다.
아래는 각각의 모델에 맞게 계산된 Perturbation을 시각화 한 것입니다. (p = ∞, ξ = 10)
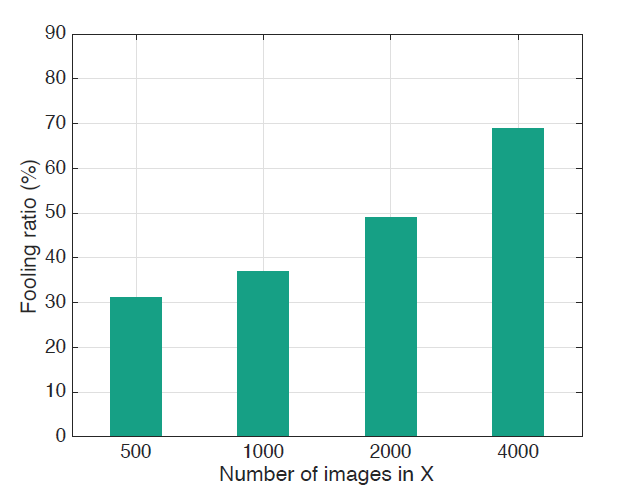
이 논문은 Data X의 사이즈가 universal perturbation에 미치는 영향에 관해서도 다루고 있습니다. 아래의 표는 다른 크기의 X에 대해서, validation data로 검증한 결과인데요, 500장으로 훈련 시킬때에도 30프로 정도의 fooling rate를 달성하였습니다. 이러한 결과는 처음보는 image dataset에 대해서도, X에 클래스당 이미지를 1개씩만 주어도 속일 수 있다고 합니다. 즉 unseen data points에 대해서 놀라운 일반화 능력을 가지고 있으며, 적은 이미지로도 계산이 가능하다고 설명하고 있습니다.
Cross-model universality
이 부분은 특정 모델에서 계산된 universal perturbation이 다른 모델에서도 적용 가능하다는 점을 보여주고 있습니다. 아래의 표는 각 모델에서 생성된 perturbation을 다른 모델에 적용했을때의 fooling rate을 보여주고 있습니다
VGG-19같은 경우에는, 다른 모델에 대해서 최소 53%이상의 fooling rate를 달성했습니다. 만약 알려지지 않은 새로운 neural network를 속이려 한다면, VGG-19로부터 계산된 perturbation에 simple addition을 통하여 misclassify가 가능할 것이라 합니다.
Visualization of the effect of universal perturbation
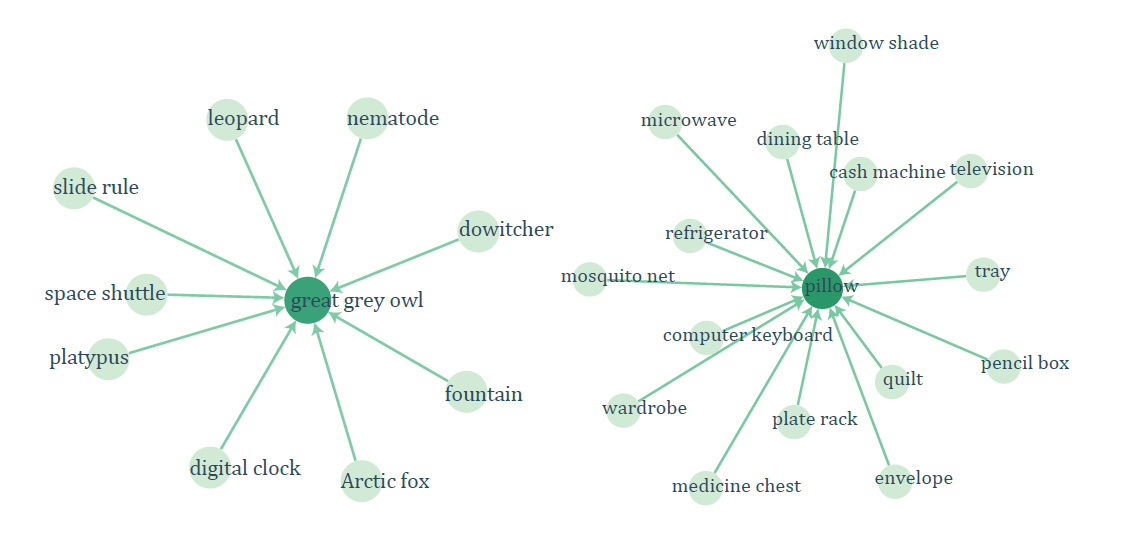
위 그래프는 perturbation 결과를 나타낸 것입니다. Vertices는 label, Edges(i->j)는 class i의 이미지들이 j로 오분류 되는 것을 보여줍니다.
Fine-tuning with universal perturbations
이 부분은 perturbated된 이미지들로 networks들을 fine-tunning한 영향에 관하여 설명하고 있습니다. 이 논문은 VGG-F 아키텍쳐를 사용하여, 처음에는 clean samples로 훈련시키고, 이후에는 (original image 0.5) + (perturbation 0.5)를 한 결과를 훈련시켰다고 합니다. Perturbation의 diversity를 높이기 위해서, 미리 계산된 10개의 universal perturbation을 바탕으로 random하게 train sample에 더해주는 방식을 사용했다고 합니다. 신경망은 5 epochs만큼 수정된 training datset을 학습하여, fine-tuned 시켰습니다. Perturbation에 fine-tuned된 모델에 대하여, 새로운 universal perturbation을 구하고 attack 해본 결과, 기존 93.7%(fine-tune 되기 전)에서 76.2%(fine-tune 이후)로 fooling rate이 떨어진 것을 보였다고 합니다. Fine-tune을 통해서 약간의 robustness의 향상은 있었으나, 이 간단한 방법은 universal perturbation에 대해 완전한 면역을 갖게 할 수는 없다고 합니다.
4. Explaining the vulnerability to universal perturbations
이 섹션은 deep neural network classifier들의 universal perturbations에 대한 취약성을 설명하고 있습니다. Universal perturbations에 설명하기 앞써, 먼저 random perturbations, adversarial perturbation(DeepFool, FGSM)을 이용한 perturbations과 비교하며 설명합니다.
각각의 방식을 CaffeNet에 적용한 Fooling rate 결과는 아래와 같습니다.
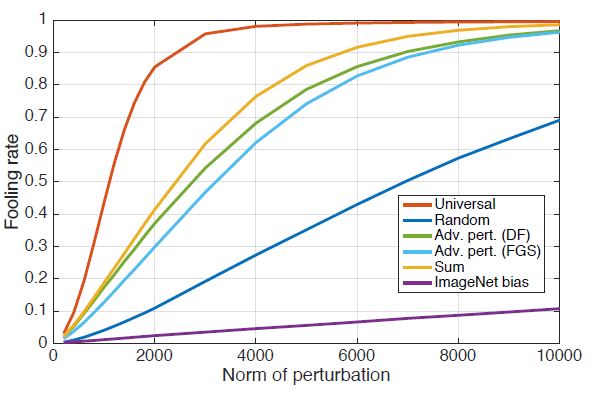
먼저 이 논문서 제시한 universal Perturbation은 빠르게 높은 fooling rate에 도달하였습니다. 특히 ξ = 2000일 때, fooling rate 85%를 달성하였습니다. 반면에 다른 방식은 fooling rate이 한참 낮은 것을 확인 가능합니다. Universal perturbation과 다른 방식의 차이점으로는, classifier의 다른 decision boundary에 대해 기하학적인 상관관계를 이용한다는 점입니다. 만약 decision boundary의 방향이 이웃한 data points들과 uncorrelated하고 decision boundary와의 거리와 무관하다면, random perturbation과 비슷할 것입니다. Random perturbation의 경우 특정한 data point를 속이기 위한 complexity는 Θ(√d||r||2)이며, d는 input space의 차원, ||r||2는 data point와 decision-boundary 사이의 거리입니다. 만약 이것을 ImageNet classification에 적용해보면, √d||r||2 ≈ 2 x 10의 4제곱만큼 task를 해야하는데, 이것은 universal perturbation을 모든 점에 대해 적용했을 때 보다도 큽니다.
이미지 x에 대한 perturbation vector r(x)는 아래와 같이 구할 수 있습니다.
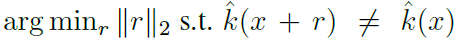
r(x) 벡터는 data point x를 둘러싸는 지역의 decision boundary의 local geometry의 정보를 담고 있습니다. different region과 decision boundary의 상관관계를 수량화하기 위해, validation set속 n개의 data point에 대한, decision boundary의 normal vector들을 matrix를 이용하여 다음과 같이 정의하였습니다
아래의 표는 decision boundary의 normal vectors를 포함하는 matrix N에 대한 singular values에 대한 그래프입니다.
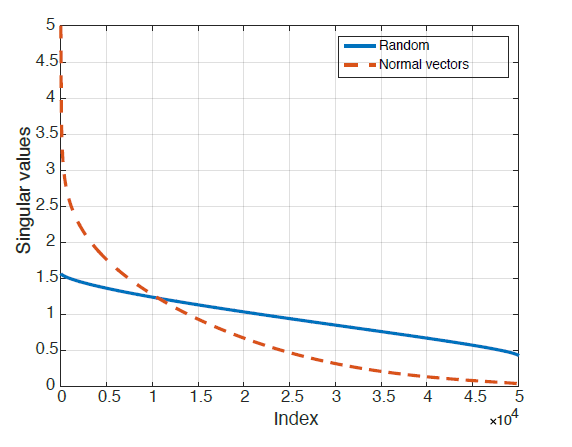
matrix N에 대한 Singular values가 빠르게 감소하는데, 이는 deep networks의 decision boundary의 상관관계를 보여주고 있다고 합니다. 즉, decision boundary의 normal vector들을 포함하는 d'(d'<<d)차원의 subspace S의 존재를 가리키고 있다고 합니다. 이 논문에서는 이러한 subspace가 natural images들을 속일수 있는 원인으로 가정하고 있습니다.
실제로 이 가설을 증명하고자, subspace S에 속한 임의의 singular vector 100개를 span시켜, 다른 image set에 대해 fooling ratio를 계산해보았는데, 38%의 결과를 얻었다고 합니다.
위의 그림은 subspace S가 decision boundary에 대한 상관관계를 담고있다는 것을 보여주는 그림입니다. data points x(i)에 대해서 decision boundary와 수직인 perturbation r(i)를 더해주면, 각각의 decision-boundary 초평면 β(i)밖으로 보낼 수 있습니다. perturbation vector r(i)는 모두 subspace S에 존재합니다.
summary
결국 natural images classifier들의 decision-boundary(초평면)에 수직한 vectors들을 많이 포함하고 있는, 저차원의 subspace S의 존재가 가장 중요한 것 같습니다. 이로 인해 적은 samples들로도 generalization이 가능한 이유라고도 합니다. Universal perturbation은 subspace S에 있는 random vector를 선택하는 것이 아닌, fooling rate를 maximize하도록(decision boundary를 넘도록) subspace S의 vector를 선택하는 방식입니다.
5. Conclusions
논문은 small universal perturbations을 통해 natural image classifier를 많이 속이는 것을 보여주었습니다. Iterative한 방법을 이용하여 universal perturbation을 구하였으며, 또한 이것이 image-agnostic, network-agnostic 하다는 것을 보여주었습니다. (across images, architectures)
원리를 또한 다른 regions의 decision-boundary간의 기하학적인 상관관계를 이용하여 설명하였습니다. 이 상관관계에 대해 추가적인 연구가 필요하다고도 설명하고 있습니다.
