이분 탐색에 대해 너무 대충 생각하고 넘어가는 경우가 잦아, 따로 코테 준비 전 C++ 기준으로 정리해보려고 한다.
Binary Search (이분 탐색)이란?
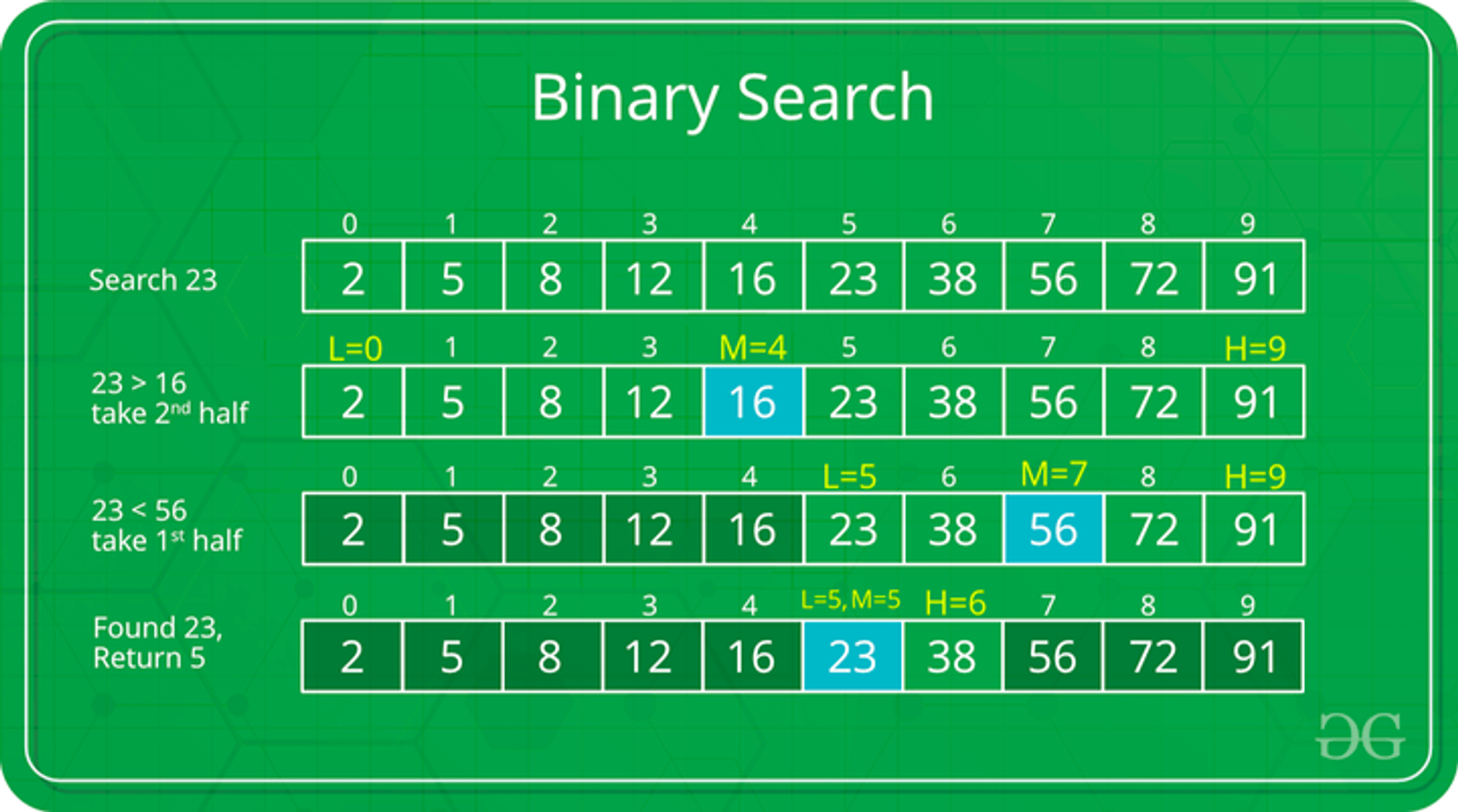
- O(N)으로 대표되는 선형 탐색이 아닌, 매 페이즈마다 계산되는 중간점을 기반으로 한 탐색 알고리즘
- 시간복잡도: O(logN)
- 주로 큰 수 범위, 특히 int 기준 10^9 등의 조건이 명시적으로 존재하는 경우, 혹은 탐색 문제인데도 단순 이중포문 O(N^2) 방식의 계산이 시간상 무리라고 판단되는 경우 꺼내들 수 있어야 한다.
- C++에서는 주로 (1) 라이브러리 함수를 활용하거나, (2) while문으로 직접 구현한다.
- 배열 등의 자료형 자체에 이분탐색을 시도하는 경우 항상 정렬이 먼저 필요하다.
라이브러리 함수
- lower_bound는 해당 key값을 찾되, 만약 없다면 이보다 큰 key 중 가장 작은 원소의 Iterator를 반환한다.
- upper_bound는 해당 key값을 처음으로 초과하는 원소의 Iterator를 반환한다.
vector에서
배열 역시 유사한 형태로 구현이 가능하나 여기선 벡터 기준으로 살펴보기로 한다.
- lower_bound(v.begin(), v.end(), val): vector v 기준으로 val 원소를 가리키는 Iterator를 반환
- 만약 존재하지 않는다면 val보다 큰 요소 중 가장 작은 요소를 가리키는 Iterator를 반환
- upper_bound(v.begin(), v.end(), val): val보다 큰 요소 중 가장 작은 요소를 가리키는 Iterator를 반환
- 실전에선 위 식에 v.begin()을 빼어 해당 값이 존재하는 index를 바로 뽑아낼 수 있음을 잊지 말자.
간단한 예시 문제를 살펴보자.
A>B인 쌍이 몇 개인지 알아내는 문제이다. 이중 for문의 경우 20000 * 20000이기에 1초 기준으로 시간초과가 필연적으로 발생하기에 이분탐색을 떠올려야 했다.
// 정렬
sort(A.begin(), A.end()); // 1 1 3 7 8
sort(B.begin(), B.end()); // 1 3 6
for(int i=0; i<n; i++){
// B에서 A의 특정 원소와 같거나 큰 원소 중 가장 작은(왼쪽) 원소의 인덱스 추출
// 0 0 1 3 3
int idx = lower_bound(B.begin(), B.end(), A[i]) - B.begin();
result += idx;
}set에서
다른 자료구조인 set과 map에도 두 함수가 존재한다.
- lower_bound(key): 특정 key와 동일한 요소를 가리키는 왼쪽으로부터 첫번째 Iterator를 반환한다.
- 만약 존재하지 않는다면, key보다 큰 요소 중 가장 작은 요소를 가리키는 Iterator를 반환한다.
- upper_bound(key): key보다 큰 요소 중 가장 작은 요소를 가리키는 Iterator를 반환한다.
- 포인터 기호(*)를 통해 해당 위치에 존재하는 값에 바로 접근할 수 있다.
set<int> s;
s.insert(1);
s.insert(2);
s.insert(3);
s.insert(5);
cout << *s.lower_bound(2); // 2
cout << *s.upper_bound(3); // 5map에서
- 마찬가지로 포인터 기호(->)를 통해 해당 위치의 값에 바로 접근할 수 있다.
map<int, int> m;
m[0] = 1;
m[2] = 3;
m[4] = 5;
cout << m.lower_bound(2)->second; // key 2가 존재하므로 해당 key의 value인 3
cout << m.upper_bound(3)->second; // key 3보다 큰 요소 중 가장 작은 key 4의 value인 5while문 직접 구현
- 아예 이진탐색 자체가 테마인 경우 필연적으로 요구되는 작업이다.
- 크게 3가지 구조로 나뉜다.
- 무엇을 이분탐색할 것인가?
- 초기 start(left)와 end(right) 결정
- 산출한 중간값 mid가 문제가 요구하는 조건을 충족하는지 판정
간단한 예제를 통해 살펴보자.
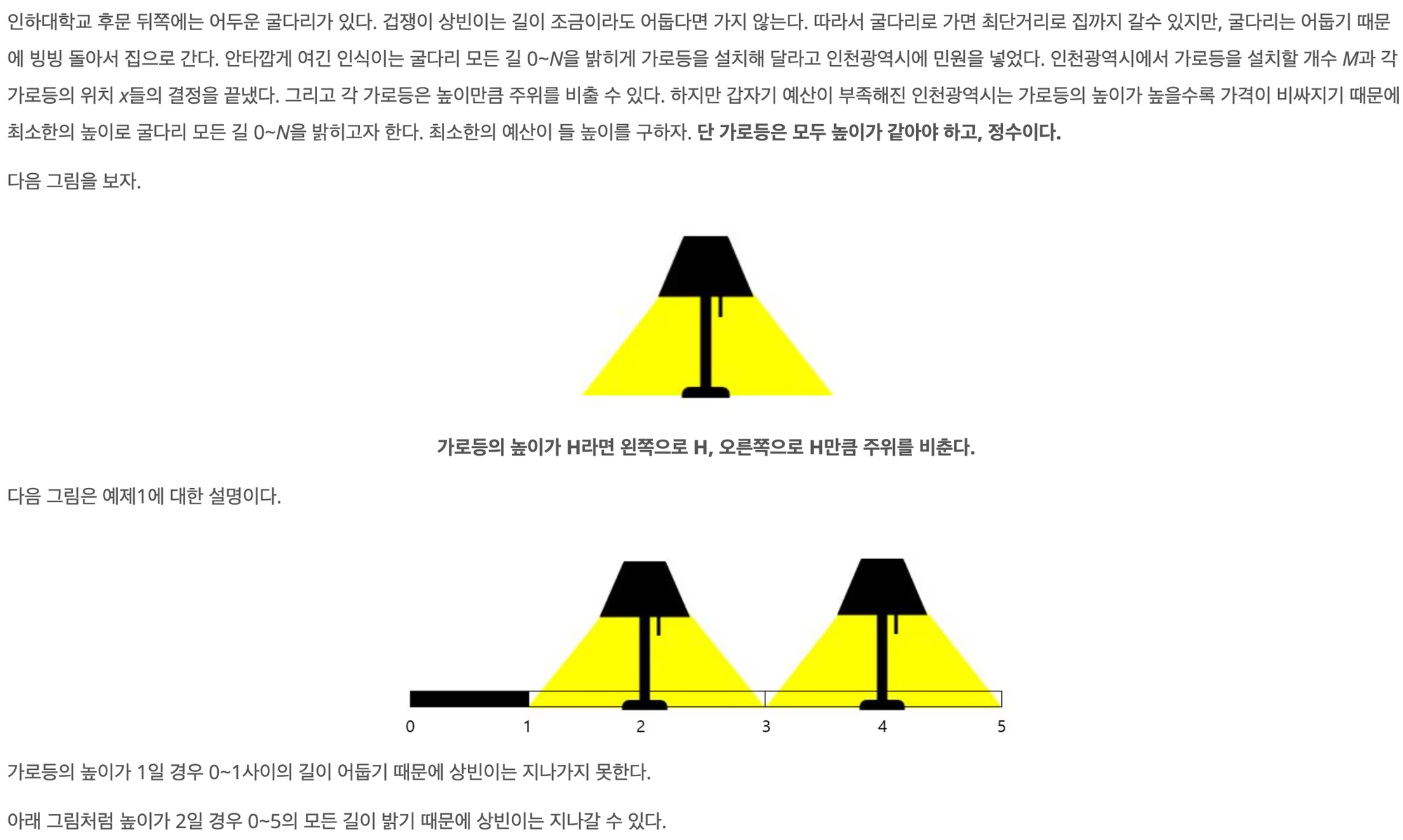
이 문제는 모든 어둠을 제거하는 가로등의 최소 높이를 찾는 문제이다. 굴다리의 최대 길이 N이 10만이고, M 역시 최대 10만이 될 수 있기에 단순 이중 for문이 어려운 상황이므로 이 역시 이분탐색을 꺼내들어야 한다.
또한 가로등은 양쪽을 동시에 밝히고 있다는 점에 유의하여 접근해보자.
- 무엇을 이분탐색할 것인가? → 가로등의 높이
- 초기 left는 0, right는 100001(최대 길이보다 1 큼)
- 중간값 mid가 충족해야 할 조건은?
- 두 가로등 사이의 거리 ≤ 2 * mid (두 가로등 사이를 모두 밝힐 수 있어야 함)
- 0과 첫번째 가로등 사이의 거리 ≤ mid (좌측 끝 영역을 모두 밝힐 수 있어야 함)
- n과 마지막 가로등 사이의 거리 ≤ mid (우측 끝 영역을 모두 밝힐 수 있어야 함)
다음은 정답 코드의 일부이다.
sort(v.begin(), v.end()); // 정렬
int l = 0; // left
int r = 100001; // right
int result = r;
while(l <= r){
int mid = (l+r) / 2;
bool flag = true;
int tmp = v[0];
for(int i=1; i<v.size(); i++){ // 두 가로등 사이 검증
if(v[i]-tmp <= 2 * mid){
tmp = v[i];
} else { // 두 가로등 사이를 모두 밝힐 수 없기에 실패
flag = false;
break;
}
}
if(v[0] > mid || n-v.back() > mid){ // 맨앞 or 맨뒤에 밝지 않은 부분 존재하므로 실패
flag = false;
}
if(flag){ // 모두 밝히는 데 성공 -> 높이(mid)가 작아져야 함
result = min(result, mid);
r = mid - 1;
} else { // 모두 밝히는 데 실패 -> 높이(mid)가 커져야 함
l = mid + 1;
}
}결론
위와 같이 특정 조건을 만족시켰거나, 특정 형태로 구간을 분할하는 등 다양한 형태로 이분탐색 테마 문제가 제시된다.
10^9와 같은 큰 숫자 범위를 갖거나, O(N^2) 연산이 어렵다는 판단이 내려질 경우 항상 이분탐색을 떠올릴 줄 알야아 하고,
이분탐색 시에는 while문을 사용해야 할지 혹은 lower_bound 등의 함수를 사용해야 할지 판단할 줄 알아야 한다.
백준 추천 문제
- lower_bound, upper_bound 활용
4158번: CD
11663번: 선분 위의 점
20551번: Sort 마스터 배지훈의 후계자
- while문을 통한 조건부 이분탐색
16564번: 히오스 프로게이머
13702번: 이상한 술집
16401번: 과자 나눠주기

우왕 멋져용><