오늘은 이분탐색에 이어 스위핑을 알아보겠다.

스위핑이란?

스위핑 (Sweeping)은 영어로 "쓸다"라는 뜻이며, 보통 한 쪽 방향부터 시작해서 다른 방향으로 진행하며 탐색하는 과정을 구현하는 상황을 의미한다.

자료형이 1차원인 경우 라인 스위핑, 2차원인 경우 평면, 3차원인 경우 공간 스위핑이라고 이야기한다.

일반적으로 정렬 및 그리디 알고리즘과 관련된 테마이며, 조건에 따라 난이도가 천차만별인 주제이기도 하다.

말로만 하면 너무 간단해 보이기에 대표적인 스위핑 문제를 예제 기준으로 다뤄보자.

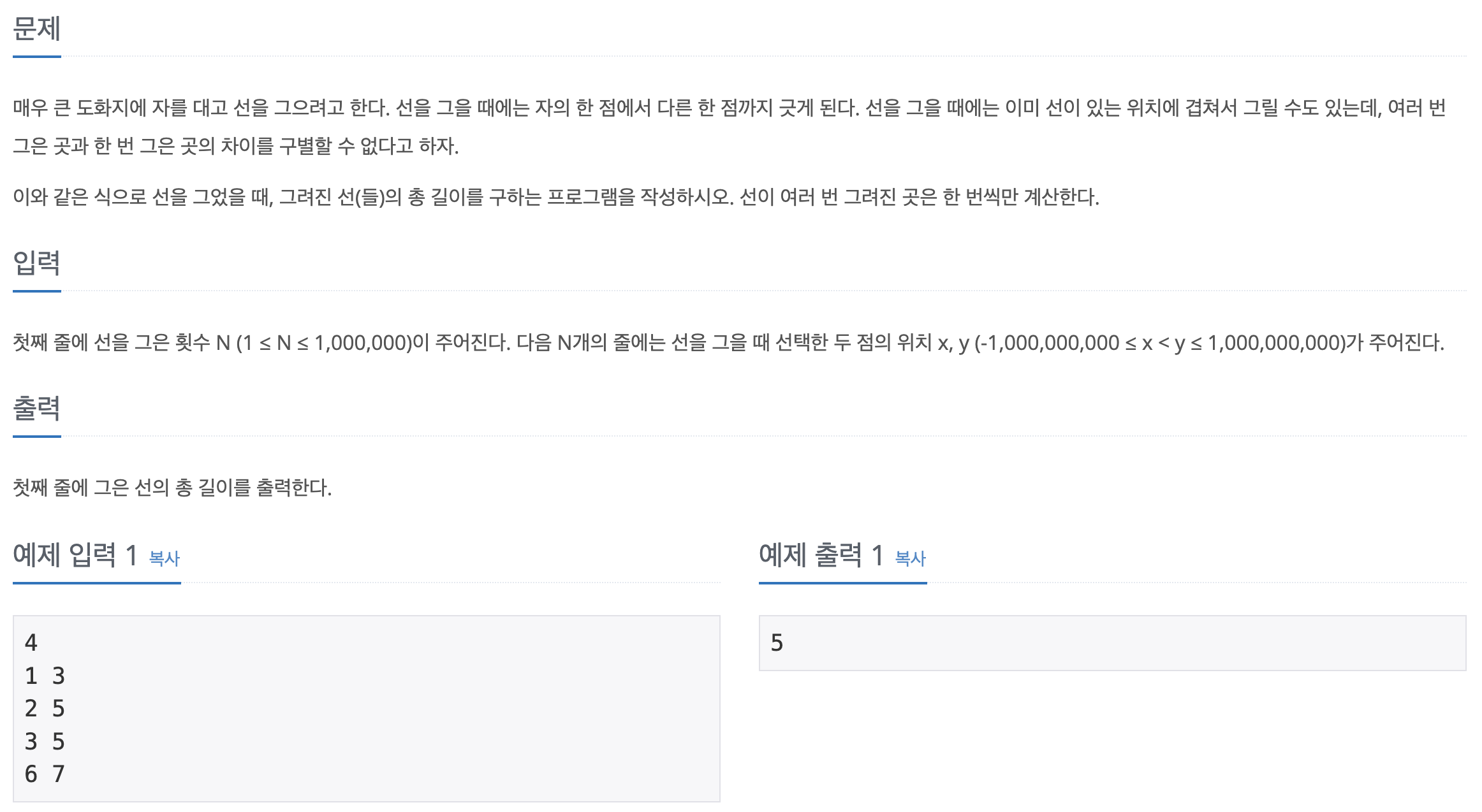
선분의 길이

가장 대표적인 유형이다.
(시작점, 끝점) 형태로 주어지는 Line을 오름차순으로 정렬한 후, 조건에 따라 병합하며 가장 긴 선분의 길이 혹은 총 선분의 합을 계산하는 유형의 문제이다.

이러한 유형은 크게 3가지 조건을 생각하면 쉽게 풀 수 있을 것이다.

• 현재 선분의 시작점이 직전 선분의 끝점보다 크다.
  (= 두 선분이 겹치지 않는다.)
• 현재 선분의 시작점이 직전 선분의 끝점보다 작다.
  (= 두 선분이 일부가 겹친다.)
• 현재 선분의 끝점이 직전 선분의 끝점보다 작다.
  (= 현재 선분이 직전 선분에 포함된다.)

예제

2170번: 선 긋기

정답 코드는 아래와 같다.

#include <iostream>
#include <algorithm>
#include <vector>

using namespace std;
int n;
long long x, y;
vector<pair<long long, long long> > v;

int main(){
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);

    cin >> n;
    for(int i=0; i<n; i++){
        long long a, b;
        cin >> a >> b;
        v.push_back(make_pair(a, b));
    }
    sort(v.begin(), v.end());

    long long sum = 0;
    long long l = v[0].first;
    long long r = v[0].second;
    if(n == 1) {
        cout << r-l;
        return 0;
    }
    for(int i=1; i<n; i++){
        if(r < v[i].first) { // 현재 시작점이 직전 끝점보다 큼 (겹치지 않음)
            sum += r-l;
            l = v[i].first;
            r = v[i].second;
        } else { // 현재 시작점이 직전 끝점보다 작음
            if(r < v[i].second) // 현재 끝점이 직전 끝점보다 큼 (선분 연장됨)
                r = v[i].second;
        }
    }
    sum += r-l; // 마지막 Case
    cout << sum;
    return 0;
}

유사한 문제가 많으니 풀어보면 금방 감을 잡을 수 있을 것이다.

15922번: 아우으 우아으이야!!
23740번: 버스 노선 개편하기
1911번: 흙길 보수하기

선분의 개수

길이와 비교했을 때 풀이법이 약간 다르다.

보통 (시작점, 1), (끝점, 0) 형태의 pair 배열을 담아 오름차순으로 정렬하고,
시작점을 감지하면 +1, 끝점을 감지하면 -1로 연산해나가며 최대 개수를 갱신한다.

어차피 시작점은 오름차순으로 등장하기에 끝점이 나오기 전에는 선분들이 점점 포개어지는 것으로 간주할 수 있기 때문이다.

1689번: 겹치는 선분

정답 코드는 아래와 같다.

#include <iostream>
#include <vector>
#include <algorithm>

using namespace std;
int n;
vector<pair<int, int> > v;

int main(){
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);

    cin >> n;
    for(int i=1; i<=n; i++){
        int s, e;
        cin >> s >> e;
        v.push_back(make_pair(s, 1));
        v.push_back(make_pair(e, 0));
    }
    sort(v.begin(), v.end());

    int nowcnt = 0;
    int answer = 1;
    for(int i=0; i<v.size(); i++){
        if(v[i].second){ // 시작점
            nowcnt++;
        } else { // 끝점
            answer = max(answer, nowcnt);
            nowcnt--;
        }
    }
    cout << answer;
    return 0;
}

19598번: 최소 회의실 개수
28070번: 유니의 편지 쓰기

이 외에도 누적 합 등과 연계된 직각다각형 등 다양한 유형이 있으므로, 1차원 Line Sweeping에 익숙해진 후엔 다양한 스위핑 유형을 직접 다루어보는 것이 큰 도움이 된다.

스위핑(특히 Line Sweeping)의 결론을 요약하자면 아래와 같다.

• 두 선분이 겹치는가?
• 일부가 겹치는가? 특정 선분이 다른 선분에 아예 포함되는가?

겹침과 관련된 정보를 빠르게 파악하면 충분히 풀 수 있다.