https://school.programmers.co.kr/learn/courses/30/lessons/42890

조합을 떠올리지 못해서 굉장히 시간을 많이 잡아먹었던 문제.

문제 설명

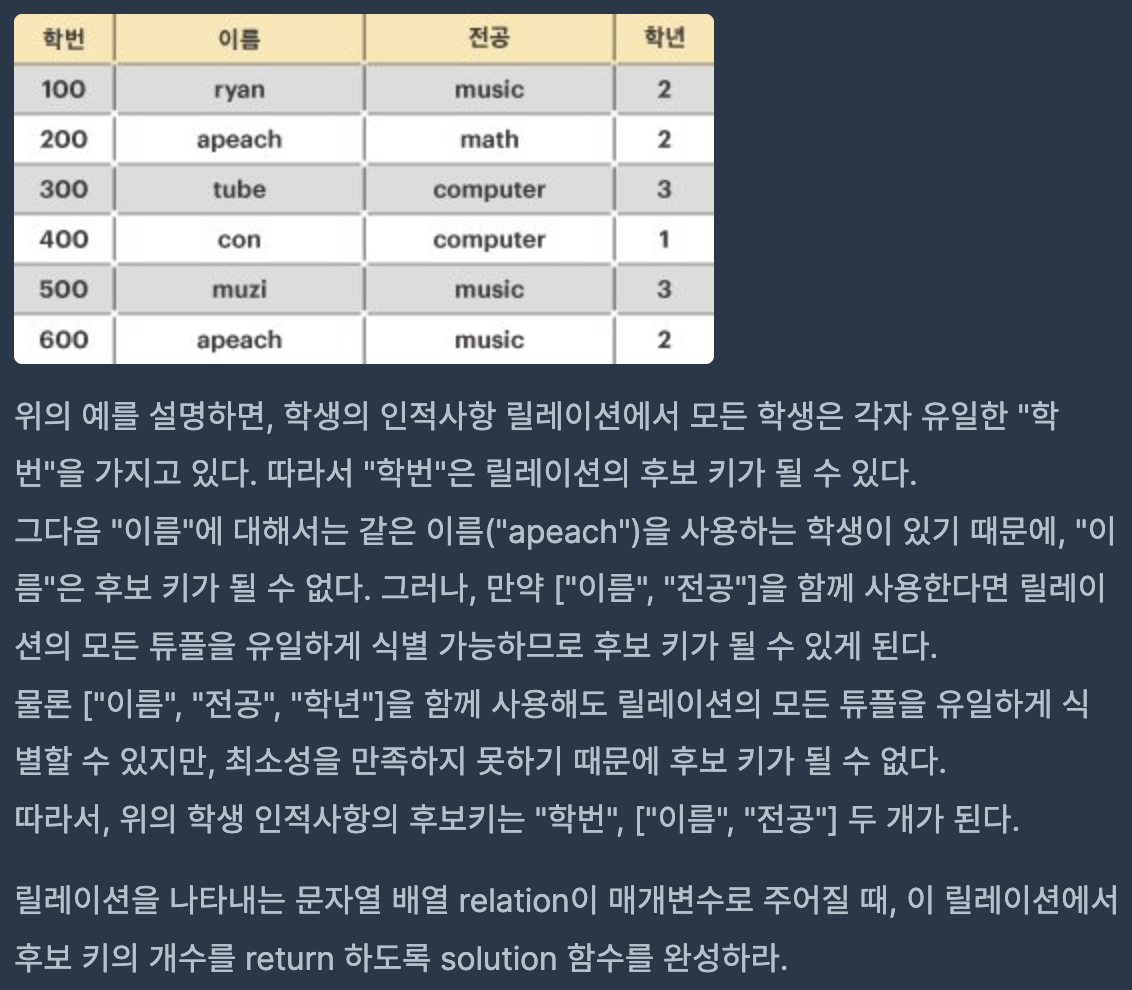
문제에서 추출할 수 있는 정보는 다음과 같다.

• 릴레이션의 컬럼 중 후보키가 될 수 있는 조합을 찾아야 한다.
• 여러 열을 합친 것이 후보키가 될 수도 있다.
• 후보키는 "유일성"과 "최소성"을 만족해야 한다.
• 유일성은 해당 후보키를 통해 입력된 모든 행이 식별되어야 함을 의미한다.
• 최소성은 최소한의 열 개수로 모든 행이 식별되어야 함을 의미한다.

해결 과정

크게 2가지 과정으로 나눌 수 있다.
1. n개의 열 중 중복 없이 1~n개의 열을 선택하는 경우의 수 찾기
2. 선택을 마쳤다면 해당 선택 case가 "유일성"과 "최소성"을 만족하는지 파악

1번째 과정은 dfs를 통한 조합으로 간단하게 구현할 수 있다. (이걸 떠올리지 못해서 크게 헤맸다.)

void dfs(int idx, int cnt, int size){
    if(cnt == size){
        if(unique() && minimal()) answer++;
        return;
    }
    
    for(int i=idx; i<m; i++){
        if(visited[i]) continue;
        visited[i] = true;
        v.push_back(i);
        dfs(i, cnt+1, size);
        v.pop_back();
        visited[i] = false;
    }
}

int solution(vector<vector<string>> relation) {
    map = relation;
    n = map.size();
    m = map[0].size();
    for(int i=1; i<=n; i++){
        dfs(0, 0, i);
    }
    return answer;
}

2번째는 유일성과 최소성을 판정하는 과정이다.

먼저 유일성은 선택된 열들의 필드값을 하나의 String에 모두 이어붙인 뒤, 해당 값이 이전에 존재했는지 Set을 통해 판정했다. 이후 유일성을 갖는다는 것이 확인되면 추후 최소성 판정을 위해 해당 조합을 따로 저장해두었다.

bool unique(){
    set<string> s;
    for(int i=0; i<map.size(); i++){
        string now = "";
        for(int j=0; j<v.size(); j++){
            now += map[i][v[j]];
        }
        if(s.find(now) == s.end()) s.insert(now);
        else return false; // 이전에 존재함 -> false
    }
    c.insert(v); // 최소성 판정을 위해 해당 조합을 저장
    return true;
}

다음으로 최소성이다. 최소성을 만족한다는 것은 최소한의 열만 골라서 전체 행의 식별이 가능하단 의미이다. n개 중 1개만 골라도 식별이 가능하다고 해도, 전체 조합에선 해당 열을 포함한 복수 개의 결과를 만들어내는 케이스가 발생한다.

즉 과하게 열을 선택한 경우를 모두 배제해야 한다. 현재 선택된 조합을 구성하는 열의 개수보다 적으면서 유일성을 만족하는 조합이 이전에 존재했는지 판정하면 된다.

bool minimal(){
    for(auto it: c){
        vector<int> tmp = it;
        int len = 0;
        if(tmp.size() < v.size()){
            for(int j=0; j<tmp.size(); j++){
                if(find(v.begin(), v.end(), tmp[j]) != v.end()){
                    len++;
                }
            }
            // 더 적은 열 수로 유일성을 만족하는 케이스가 이전에 존재함
            if(len == tmp.size()) return false; 
        }
    }
    return true;
}

소스 코드

#include <string>
#include <iostream>
#include <algorithm>
#include <set>
#include <vector>

using namespace std;
int answer = 0;
int n, m;
vector<int> v;
bool visited[21];
vector<vector<string>> map;
set<vector<int>> c;

bool unique(){
    bool selected[21];
    set<string> s;
    for(int i=0; i<map.size(); i++){
        string now = "";
        for(int j=0; j<v.size(); j++){
            now += map[i][v[j]];
        }
        if(s.find(now) == s.end()) s.insert(now);
        else return false;
    }
    c.insert(v);
    return true;
}

bool minimal(){
    for(auto it: c){
        vector<int> tmp = it;
        int len = 0;
        if(tmp.size() < v.size()){
            for(int j=0; j<tmp.size(); j++){
                if(find(v.begin(), v.end(), tmp[j]) != v.end()){
                    len++;
                }
            }
            if(len == tmp.size()) return false;
        }
    }
    return true;
}

void dfs(int idx, int cnt, int size){
    if(cnt == size){
        if(unique() && minimal()) answer++;
        return;
    }
    
    for(int i=idx; i<m; i++){
        if(visited[i]) continue;
        visited[i] = true;
        v.push_back(i);
        dfs(i, cnt+1, size);
        v.pop_back();
        visited[i] = false;
    }
}

int solution(vector<vector<string>> relation) {
    map = relation;
    n = map.size();
    m = map[0].size();
    for(int i=1; i<=n; i++){
        dfs(0, 0, i);
    }
    return answer;
}

교훈

• 문제에서 백트래킹을 비롯한 순열과 조합 개념을 활용할 수 있는지 항상 체크한 뒤에 완전탐색이든 DP든 다른 개념을 떠올리자.