문제
성냥개비는 숫자를 나타내기에 아주 이상적인 도구이다. 보통 십진수를 성냥개비로 표현하는 방법은 다음과 같다.
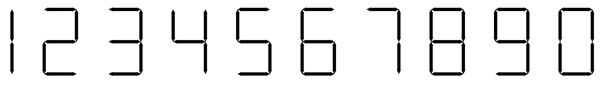
성냥개비의 개수가 주어졌을 때, 성냥개비를 모두 사용해서 만들 수 있는 가장 작은 수와 큰 수를 찾는 프로그램을 작성하시오.
입력
첫째 줄에 테스트 케이스의 개수가 주어진다. 테스트 케이스는 최대 100개 이다. 각 테스트 케이스는 한 줄로 이루어져 있고, 성냥개비의 개수 n이 주어진다. (2 ≤ n ≤ 100)
출력
각 테스트 케이스에 대해서 입력으로 주어진 성냥개비를 모두 사용해서 만들 수 있는 가장 작은 수와 가장 큰 수를 출력한다. 두 숫자는 모두 양수이어야 하고, 숫자는 0으로 시작할 수 없다.
생각
가장 큰 경우
- 자릿수가 많을 수록 크다.
- 큰 자릿수가 클 수록 크다.
성냥개비가 적게 드는 숫자를 최대한 앞에 두는 방식으로 하면 어떨까.
가장 작은 경우에서 성냥개비를 압축해야 한다면, 이건 최대한 펴는 방식이다.
1) 짝수: 1을 나열하면 된다.
2) 홀수: 가장 큰 자릿수에 7을 두고, 나머지를 1로 채우면 된다.
감사하게도 조건이 예외 여지가 없어, Greedy로 풀 수 있다.
가장 작은 경우
- 자릿수가 최대한 적어야 한다.
- 큰 자릿수가 작을 수록 작다.
이번엔 반대로, 성냥개비가 많이 드는 숫자를 뒤에 배치해보자.
그럼 이제 뭔가 이상하다.
성냥개비 개수가 많은 숫자를 선택하는게 무조건 최소값이 되지도 않거니와, 그리디로 접근하려니 자잘한 예외사항이 많이 생긴다.
결국 모든 경우를 따져봐야 한다는 결론이 나온다.
즉 Dynamic Programming으로 접근해야 한다.
Dynamic Programming 설계
- dp[i] : i개의 성냥개비를 썼을 때 나타낼 수 있는 최소값
- j : 반복문 변수 - 성냥개비 개수
- dp[i] = min(dp[i], dp[i-j]*10 + num[j])
예외 사항
성냥개비 개수가 6인 경우, 최소값은 0이지만 숫자가 0으로 시작할 수 없다는 제약이 있기 때문에 6이다.
그러나 한자리수가 아니라 중간 자리수에서 6개 최소값을 계산할 경우, 0으로 시작하지 않기 때문에 답은 0이다.
Solution
import sys
input = sys.stdin.readline
def getResult():
minimum = getMinimum(n)
maximum = getMaximum(n)
print(minimum, maximum)
def getMinimum(n):
dp = mins + [0]*92
for i in range(9,n+1):
dp[i] = dp[i-2] * 10 + 1
for j in range(3,8):
if j == 6: dp[i] = min(dp[i], dp[i-j] * 10)
else: dp[i] = min(dp[i], dp[i-j] * 10 + mins[j])
return dp[n]
def getMaximum(n):
if n % 2 == 0: result = '1' * (n // 2)
else: result = '7' + '1' * (n // 2 - 1)
return result
testCaseCount = int(input())
mins = [0,0,1,7,4,2,6,8,10]
for _ in range(testCaseCount):
n = int(input())
getResult()

