이번 시리즈는 고려대학교 산업경영공학부 강필성 교수님의 강의를 참고하였습니다. Business Analytics라는 과목이고, 데이터사이언스 분야의 내용이 잘 정리되어 있어 공부하기 좋을 것 같아 이번 시리즈를 연재하게 되었습니다. 부족한 점이 많겠지만 데이터사이언스 공부를 하는데 도움이 되었으면 합니다.
[Why Evaluate?]
[과적합]
분류 모델의 학습을 위해선 보유하고 있는 데이터를 Train data, Validation data, Test data 3개로 분리하여 Train data만을 사용한다.
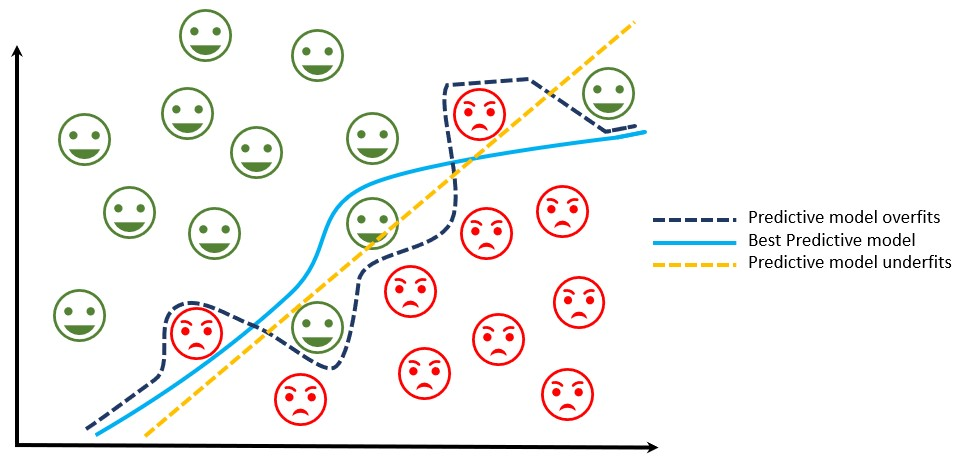
이때 위와 같이 웃음 표시인 데이터와 화난 표시의 데이터가 있을 때 파랑색 점선인 Predictive model overfit처럼 모델을 학습한다면 Train data에서는 성능이 좋겠지만 Test data에서는 좋지 않을 수 있다.
왜냐하면 모든 실제 데이터들은 다음과 같은 식을 따르기 때문이다.
여기서 은 데이터에 내재된 변동성을 의미한다. 따라서 만약 Train data만으로 파란 점선과 같이 분류 기준을 정한다면 가 아닌 을 추정하여 Test data에서는 결과가 나쁠 수 있다.
예를 들어 모의고사 기출 문제를 복습하면서 100점 맞는 거는 아무 의미가 없고, 새롭게 치르는 수능을 100점 맞아야만 의미가 있다는 것이다.
[성능 평가]
분류 문제나 회귀 문제에 있어서 다양한 모델 중 최적의 모델을 찾기 위해서이다.
[하이퍼파라미터 최적화]
신경망 모델에서 은닉층의 개수나 활성화함수 설정 등 하이퍼파라미터 설정이 필요한 모델에서 Validation data만을 이용하여 Best parameter를 탐색하는 역할을 한다.
정리하면, 모델 학습을 위해 Train data, 하이퍼파라미터 설정을 위해 Validation data, 그렇게 찾은 최적의 모델 중 어떤 모델이 좋은 지를 판단하기 위해 Test data를 사용한다는 것이다.
[Classification Performance Evaluation]
그럼 분류를 위한 평가 기준은 어떤 기준들이 있을까?
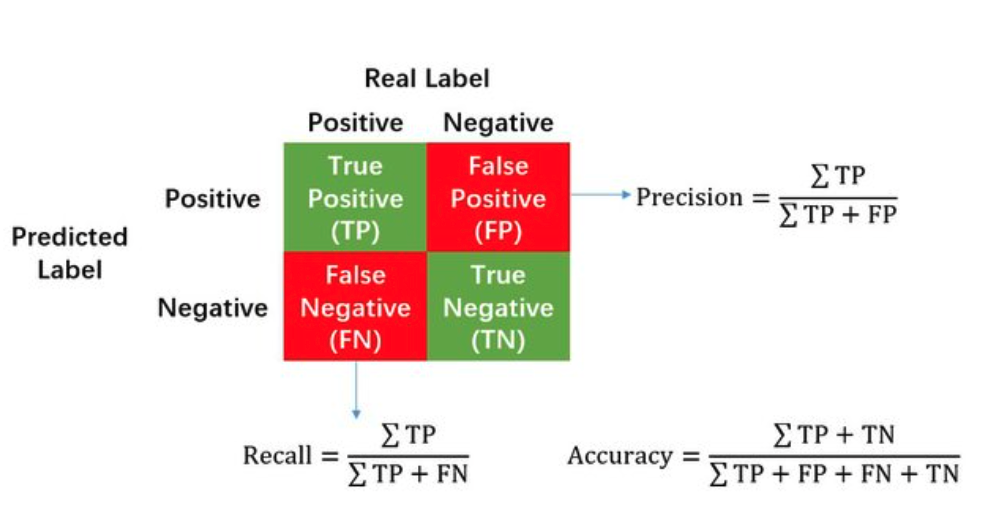
첫번째는 정확도(accuracy)가 있다.
정확도는 모델이 전체 문제 중에서 정답을 맞춘 비율로 0 ~ 1 사이의 값을 가지며, 1에 가까울수록 좋다.
하지만 데이터가 불균형할 때(ex) positive:negative=9:1)는 Accuracy만으로 제대로 분류했는지는 알 수 없기 때문에 Recall과 Precision을 사용한다.(범주 0과 1이 있으면 불균형 데이터의 경우 많은 수의 범주를 모두 맞추고 적은 수의 범주를 모두 틀려도 정확도가 높게 나옴.)
[Confusion Matrix]
Recall과 Precision을 이해하기 전에 혼동행렬(Confusion Matrix)에 대해 우선 살펴보아야 한다.
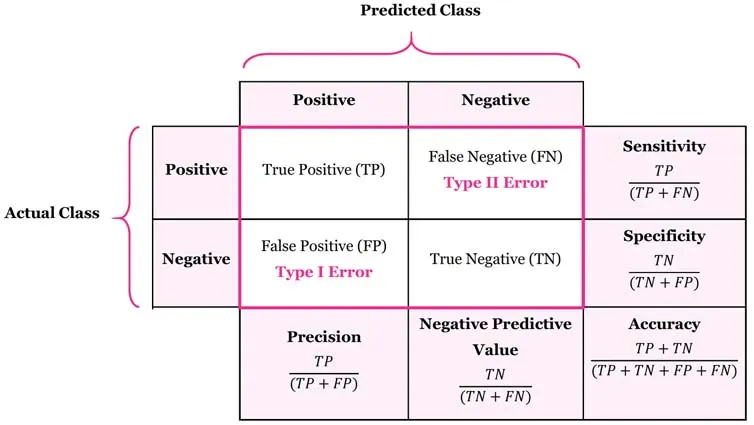
여기서 각 용어는 다음과 같다.
T(True): 예측한 것이 정답
F(False): 예측한 것이 오답
P(Positive): 모델이 positive라고 예측
N(Negative): 모델이 negative라고 예측
TP(True Positive): 모델이 positive라고 예측했는데 실제로 정답이 positive (정답)
TN(True Negative): 모델이 negative라고 예측했는데 실제로 정답이 negative (정답)
FP(False Positive): 모델이 positive라고 예측했는데 실제로 정답이 negative (오답)
FN(False Negative): 모델이 negative라고 예측했는데 실제로 정답이 positive (오답)
이를 통해 범주별 정확도를 비롯한 다양한 평가지표로 계산이 가능하다.
두번째 평가지표인 Recall(재현율)은 실제로 정답이 positive인 것들 중에서 모델이 positive라고 예측한 비율이다. 해당 평가지표는 실제 정답이 positive인 데이터를 negative라고 잘못 예측하면 안 되는 경우에 중요한 지표가 될 수 있다. 재현율이 유용한 분야는 예를 들어 암 검진 기기 등의 분야가 있다.
Recall를 높이기 위해선 FN(모델이 negative라고 예측했는데 정답이 positive인 경우)을 낮추는 것이 중요하다. 식은 다음과 같다.
세번째 평가지표는 Precision(정밀도)입니다.
모델이 positive라고 예측한 것들 중에서 실제로 정답이 positive인 비율이다. 이는 실제 정답이 negative인 데이터를 positive라고 잘못 예측하면 안 되는 경우에 중요한 지표가 될 수 있다.
Precision을 높이기 위해선 FP(모델이 positive라고 예측했는데 정답은 negative인 경우)를 낮추는 것이 중요하다.
네번째 평가지표는 Balanced correction rate(BCR)로 이는 범주별 정답의 비율을 고르게 반영시켜주는 평가지표이다. 식은 다음과 같다.
다섯번째 평가지표는 F-1 Score이다.
F-1 Score은 Recall과 Precision의 조화평균으로 Recall과 Precision은 상호 보완적인 평가 지표이기 때문에 F1 score를 사용한다. Precision과 Recall이 한쪽으로 치우쳐지지 않고 모두 클 때 큰 값을 가진다. 식은 다음과 같다.
[Cut-off]
위의 평가지표들은 모두 이 Cut-off의 영향을 받는다.
Cut-off란 말 그대로 "분류 기준"을 의미한다.
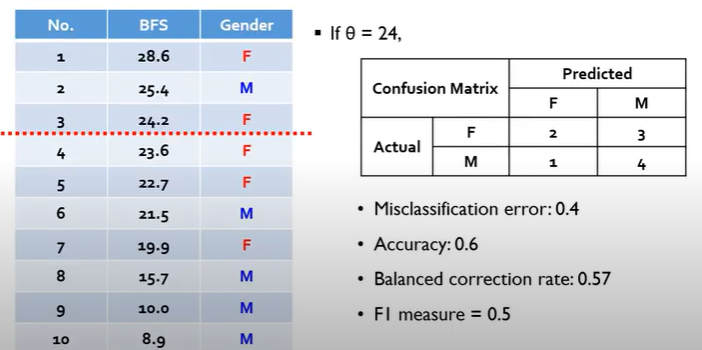
예를 들어 다음과 같이 BFS에 따라 Gender를 구분하는 문제가 있다고 하자. 이때 Cut-off 기준을 24로 한다면 위의 3개의 행은 F(female)로, 나머지는 M(male)로 구분된다.
따라서 오른쪽 혼동행렬과 같은 표가 구해진다.
이때 만약 Cut-off 기준을 22로 수정하면 다음과 같이 결과가 달라진다.
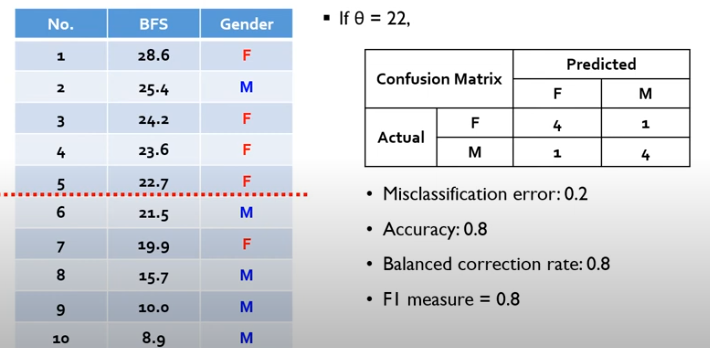
즉, 정확도(Accuracy)와 BCR, f-1 score은 Cut-off 기준에 Dependent하다는 것을 의미한다.
이때 Model Selection & Model comparison 과정에서 Cut-off 기준에 따라 평가지표가 Dependent하다면 분석가의 주관에 따라 결과가 달라질 수 있다.
따라서 이때 Cut-off와 독립적인 평가지표가 바로 ROC courve이다.
[ROC Curve]
우리는 이때 이를 이해하기 위해 생산품의 불량 판단 문제를 풀어보고자 한다.
교수님이 사용하신 데이터는 100개의 생산품 중 20개가 불량품인 데이터이며 1일 때 불량, 0일 때가 정상이다. 그리고 이때 평가지표로 AUROC(Area Under Receiver Operating Characteristic Curve)를 사용한다.
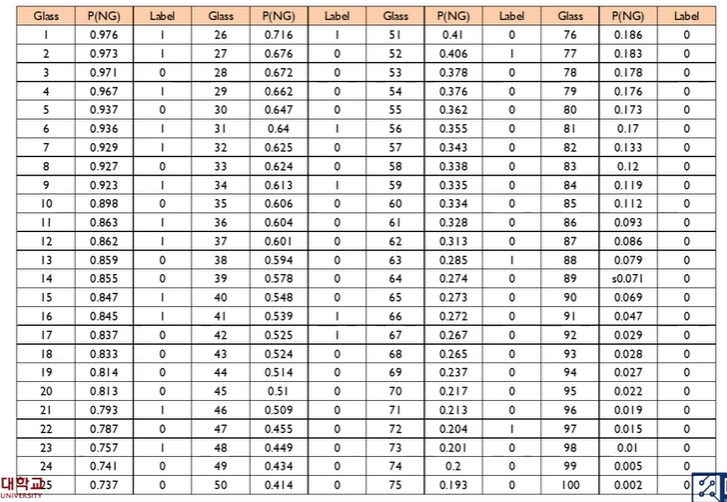
데이터 셋은 위와 같으며 P(NG)는 로지스틱 회귀분석 결과로 나온 불량품일 확률, Label은 실제 레이블을 의미한다. 따라서 Best Model은 20까지 모두 실제 레이블이 1이고 그 아래는 0이겠지만 실제 분석은 그럴 가능성이 매우 적다.
그러므로 우리는 최대한 Cut-off 위에는 label 1이 많고 아래에는 0이 많게 설계해야한다. 이때 역시 Cut-off에 따라 정확도는 아래와 같이 달라질 수 있다.
1) Cut-off가 0.9
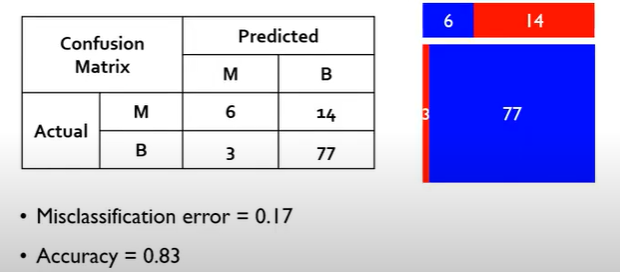
2) Cut-off가 0.8
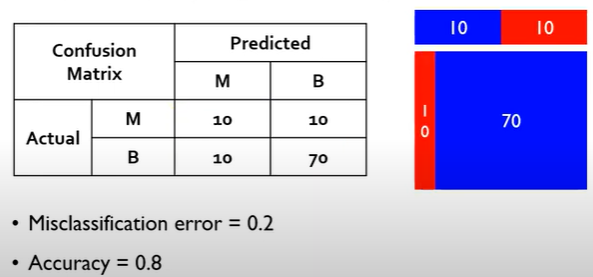
이렇게 정확도가 달라진다면 이는 Performance를 측정하는 기준으로 옳지 않을 수 있다.
따라서 ROC Curve를 사용한다면 이를 해결할 수 있다.
그럼 ROC Curve가 무엇이냐.
P(NG)를 내림차순으로 정렬하고 Cut-off를 다르게 바꿔가며 TPR(True Positive ratio)을 Y축, FPR(False Positive Ratio)을 X축으로 함께 보며 이를 차트로 시각화하는 것이다.
이때 , 으로 계산된다.
다시 이어가서, 만약 데이터가 100개 있다면 총 101개의 Cut-off 기준이 존재한다.
따라서 첫 Cut-off 기준은 다음과 같이 혼동행렬이 구성되어 (0,0)에서 시작된다.
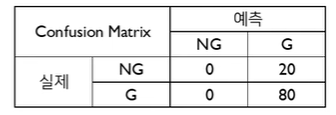
-> TPR = , FPR =
다음 두번째 Cut-off 기준은 다음과 같이 혼동행렬이 계산된다.
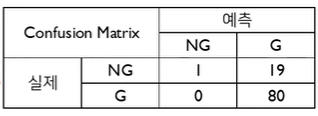
-> 이때 TPR = , FPR =
다시 4번째 Cut-off 기준을 살펴보면 다음과 같이 혼동행렬이 계산된다.
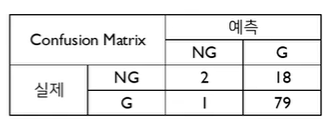
-> 이때 TPR = , FPR =
따라서 다음과 같이 결과가 구해진다.
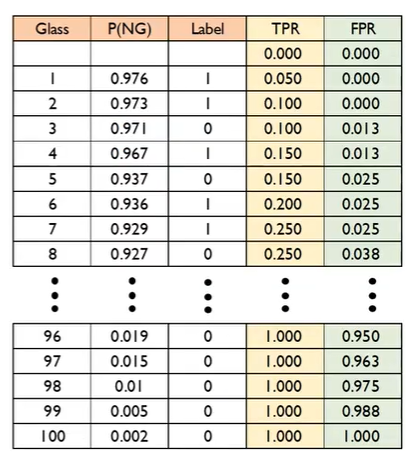
그럼 결국 마지막 Cut-off는 (1,1)로 계산되고 다음과 같이 시각화할 수 있다.
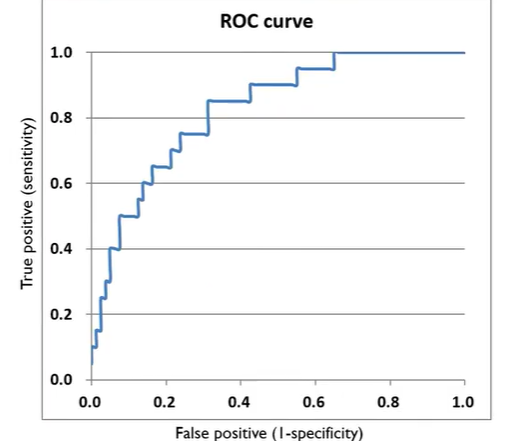
이때 만약 좋은 분류기면 아래의 보라색 선과 같고, Random 즉, 아무 의미 없는 분류기의 경우 아래 빨간 점선과 같은 ROC curve가 나타난다. 따라서 모든 ROC Curve는 Perfect Classifier와 Random Classifier 사이로 지나가게 된다.
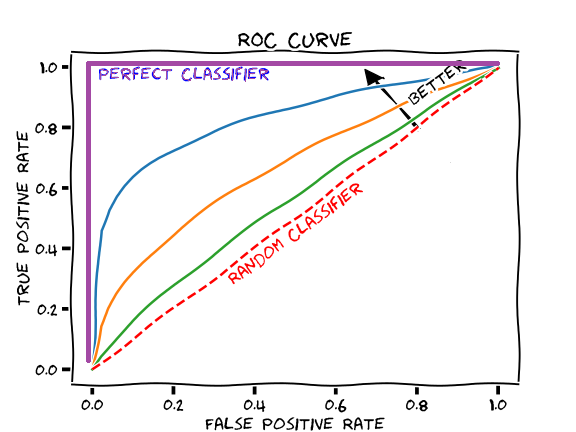
이때 사람들은 ROC Curve를 보고 이해할 수 있지만 컴퓨터는 그렇지 못하다. 그래서 등장한 개념이 바로 AUROC이다. 이는 ROC Curve 아래 면적을 계산하는 것이다. 따라서 대부분의 분류기는 1과 0.5 사이의 AUROC 값이 나오게 된다.
