이번 시리즈는 고려대학교 산업경영공학부 강필성 교수님의 강의를 참고하였습니다. Business Analytics라는 과목이고, 데이터사이언스 분야의 내용이 잘 정리되어 있어 공부하기 좋을 것 같아 이번 시리즈를 연재하게 되었습니다. 부족한 점이 많겠지만 데이터사이언스 공부를 하는데 도움이 되었으면 합니다.
[이론적 배경]
로지스틱 회귀 1편에 이어서 Gradient descent의 이론적 배경부터 다뤄보도록 하겠습니다.
[Learning]
[Taylor expansion]
Taylor expansion(테일러 전개)는 Δw가 매우 작은 값일 때 다음과 같은 식으로 나타낼 수 있음을 의미합니다.
f(w+Δw)=f(w)+1!f′(w)Δw+2!f′′(w)(Δw)2+ ⋯(1)
이때 Δw가 매우 작다면 2차항을 포함한 그 이상의 고차항들은 0으로 수렴하게 됩니다.
만약 1차 도함수가 0이 아니면, 아래를 통해 가중치를 업데이트할 수 있습니다.
wnew=wold−αf′(w),where0<α<1(2)
여기서 −f′(w)는 "방향"을 의미하고 α는 "크기"를 의미합니다.
따라서 (1)식에 (2)를 대입하면 다음과 같이 나타납니다.
f(wnew)=f(wold−αf′(wold))≃f(wold)−α∣f′(w)∣2<f(wold)
조금 더 상세히 설명하자면 −αf′(wold)를 (1)의 Δw라고 생각할 수 있습니다.
따라서 f(wold−αf′(wold))가 f(wold)−α∣f′(w)∣2로 다음과 같은 과정을 통해 근사하게 됩니다.
f(wold−αf′(wold))≃f(wold) + 1!f′(wold)⋅−αf′(wold)=f(wold)−α∣f′(w)∣2
[로지스틱 회귀에서의 적용]
이를 독립변수가 2개인 로지스틱 회귀에 적용하면 다음과 같습니다.
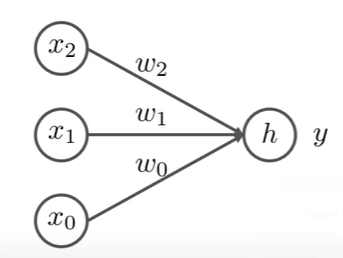
여기서, xi가 3개인 이유는 x0은 상수항 즉, 1을 의미하기 때문이며 h와 y는 다음과 같습니다.
h=i=0∑2wixiy=1+exp(−h)1=σ(X∣w)
- h의 wi는 사실상 로지스틱 회귀분석의 βi를 의미하며, y는 로지스틱 회귀식임을 알 수 있습니다.
→ 쉽게 말해, 그냥 독립변수 2개로 로지스틱 회귀분석한 것!
이때 Cost function을 아래와 같다고 가정해보자
L=21(t−y)2
여기서 t는 종속변수인 0 or 1이고, y는 p(y=1)로 t=1인 경우에는 p(y=1)이 1에 가깝게 나오면 좋고, t=0인 경우에는 p(y=1)이 0에 가까울수록 좋은 비용함수입니다.
그럼 우리는 위 Cost function을 활용하여 가중치를 업데이트를 해야하고, 그러기 위해선 ∂wi∂L를 계산해야합니다.
Cost function L에는 w에 관한 식이 없지만 다음과 같은 Chain rule를 통해 계산할 수 있습니다.
∂wi∂L=∂y∂L×∂h∂y×∂wi∂h
여기서 각 ∂y∂L,∂h∂y,∂wi∂h의 계산 과정은 아래와 같습니다.
L=21(t−y)2 → ∂y∂L=y−t
몫의 미분법에 따라,
∂h∂y=(1+exp(−h))2exp(−h)=1+exp(−h)1⋅1+exp(−h)exp(−h)=y(1−y)
h=wixi → ∂wi∂h=xi
따라서, 우리는 다음과 같은 식을 도출할 수 있습니다.
∂wi∂L=∂y∂L×∂h∂y×∂wi∂h=(y−t)⋅y(1−y)⋅xi
그러므로 우리는 가중치 wi를 다음과 같이 업데이트를 할 수 있습니다.
wnew=wold−α∂wi∂L=wold−α×(y−t)⋅y(1−y)⋅xi
여기서, (y−t)는 예측값인 y과 실제값인 t로 이루어진 항으로 예측값과 실제값의 차이를 나타내는 항입니다. 이때 만약 그 차이가 작다면 가중치 업데이트의 양 역시 줄이는게 합리적이라고 생각할 수 있습니다.
그러므로 Update the coefficient more if the current output y is very different from the target t
즉 조절할 가중치의 변화량을 의미합니다.
다음으로 xi항은 Update the coefficients more if the value of corresponding input variable is large
즉, 가중치 조절에서 연관된 독립변수의 값만 영향을 미친다는 것입니다. 예를 들어 로지스틱 회귀식에서 β2^를 추정하는데 있어서, x1이나 x3는 영향을 주지않고 x2만이 영향을 준다는 의미입니다.
[Prediction]
성공확률 p는 로지스틱 회귀식에 따라 다음 식을 통해 예측됩니다.
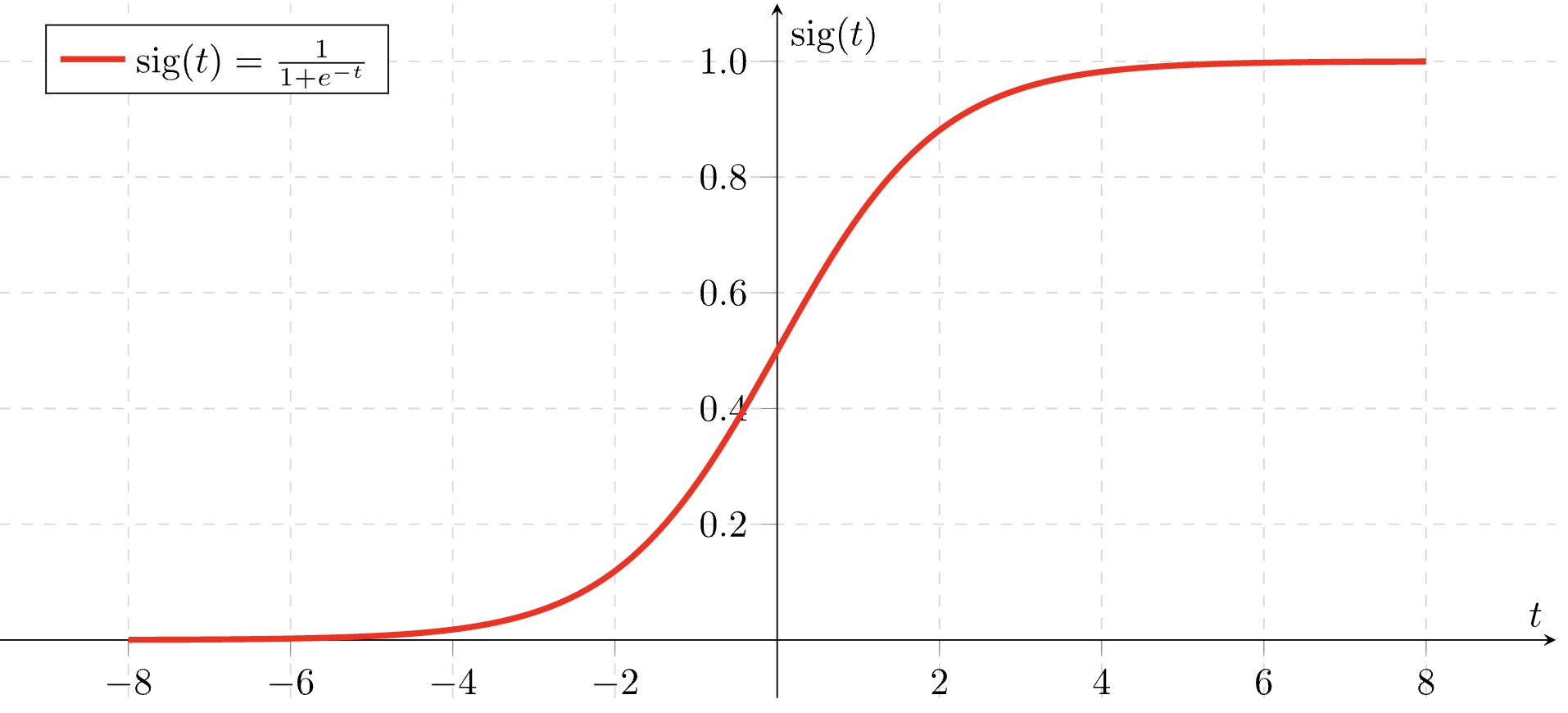
p=1+e−(β0^+β1^x1+β2^x2⋯βd^xd)1
따라서 새로운 데이터가 들어왔을 때 위 식을 통해 두 범주 중 한 범주에 속할 확률을 구할 수 있습니다.
여기서 위 그림의 x축은 β0^+β1^x1+β2^x2⋯βd^xd을 의미하며, y축은 p를 의미합니다.
이때 현실에서는 어떤 변수에 대해 항상 선형적으로 증가하는 것이 아닌 특정 구간에 대해서만 선형성을 가지는 경우가 빈번합니다.
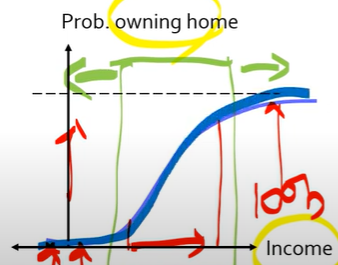
예를 들어 위 그림을 보면 초록색 구간보다 왼쪽에서는 x축의 값이 증가하더라도 y축의 값이 많이 상승하지 않습니다. 이는 소득이 적은 구간에서는 아무리 소득이 증가하더라도 집을 구매하기가 어렵다는 것을 의미합니다.
하지만 초록색 구간에서는 소득이 증가하는 만큼 집을 소유할 확률도 함께 올라가는 선형성을 보입니다. 또한 초록색구간보다 오른쪽은 소득이 많은 구간으로 이미 그 구간의 대부분이 집을 소유하고 있을 확률이 높기 때문에 x축의 값이 떨어진다고 해도 y축의 값이 크게 떨어지지는 않는 모습을 보입니다.
[Cut-off]
로지스틱 회귀를 통해 한 범주에 속할 확률 p를 계산한 후에는 p값에 따라 한쪽 범주로 할당해줘야 합니다.
즉, 0.76과 같이 확률값으로 산출되는 결과를 0 or 1로 나타내줘야한다는 의미입니다. 이를 Cut-off 또는 threshold라고 합니다.
일반적으로는 0.5로 기준을 정의해주지만, 제조업과 같은 분야에서는 정상/불량 판단에 있어서 불량이 매우 적습니다.
이러한 경우 0.5를 cut-off 기준으로 사용하면 불량으로 너무 많이 판단됩니다. 따라서 그 기준을 옮길 필요가 있습니다. 보통은 우리가 관심있는 범주를 "1"범주로 지정을 하는데, 제조업의 경우 불량 범주가 "1"범주가 됩니다.
이 경우 대부분 현실 문제에서는 관심있는 범주에 속하는 수가 적은 경우가 많습니다. 따라서 Cut-off 기준을 0.5보다 낮은 값으로 정하여 이를 해결합니다.
이때 정확한 Cut-off 기준에 대해 정답은 없지만 Classification accuracy가 최대가 되거나 Sensitivity와 같은 값이 최대화가 되도록 하는 값을 기준으로 사용합니다.
[Interpretation]
위 과정들을 거쳐 회귀 계수를 추정했으니 그러면 회귀 계수가 무엇을 의미하는지에 대해서도 알아봐야겠죠??
선형 회귀 식
y^=β0^+β1^x1+β2^x2+⋯+βd^xd
에서 β^는 설명변수가 한 단위 증가했을 때 변화하는 종속변수(y^)의 양입니다.
반면, 로지스틱 회귀식
log(Odds)=log(1−pp)=β0^+β1^x1+β2^x2+⋯+βd^xd
은 좌변이 log(Odds)이기 때문에 회귀계수의 의미를 직관적으로 파악하기 어렵습니다.
그래서 로지스틱 회귀에선 Odds ratio라는 개념이 사용됩니다.
예를 들어 x1 한 단위가 증가할 때 Odds ratio 식은 아래와 같습니다.
Odds(x1,⋯,xd)Odds(x1+1,⋯,xd)=eβ0^+β1^x1+β2^x2+⋯+βd^xdeβ0^+β1^(x1+1)+β2^x2+⋯+βd^xd=eβ1^
의미를 알아보면, x1 한 단위가 증가할 때 Odds는 eβ1^만큼 증가한다는 뜻입니다.
이때 만약 β^>0이라면 eβ^>1를 만족하고, 이는 결국 Odds ratio가 커진다는 것을 의미하며 이는 성공확률 p가 증가한다는 의미입니다.
따라서, β^>0인 경우는 "성공" 범주와 회귀계수 간에 양의 상관관계가 있음을 의미합니다. 또한 만약 반대로 β^<0인 경우에는 eβ^<1이며 이는 위와 같은 과정을 통해 "성공"범주와 회귀계수 간에 음의 상관관계가 있다는 것을 의미하게 됩니다.
그럼 예시를 통해 다시 이해해보도록 하겠습니다.
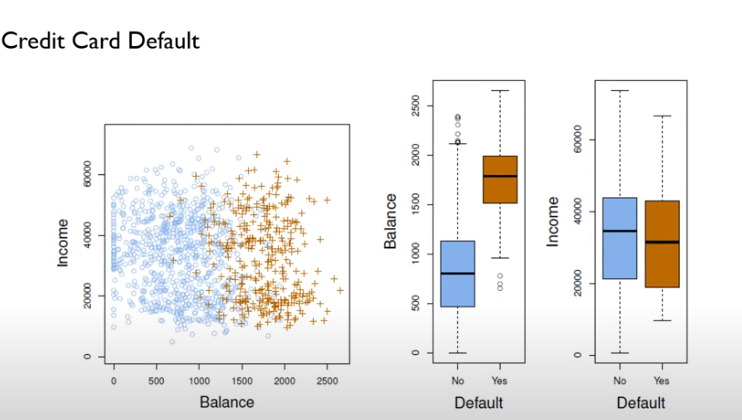
만약 파란색 동그라미는 Not Default, 주황색 십자표시는 Default한 사람들의 데이터라고 할 때, 산점도와 Boxplot을 살펴보면 Balance 변수는 Default 판단에 있어 매우 유용한 변수이지만 Income 변수는 두 범주를 명확하게 구분할 수 없기 때문에 유용하지 않은 변수인 것을 파악할 수 있습니다.
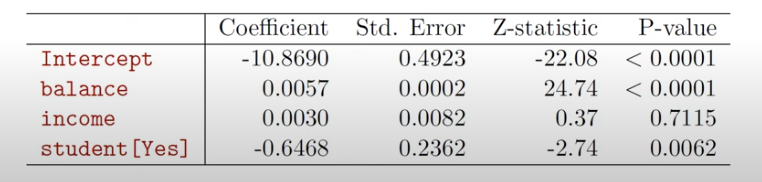
위 변수들과 Student 변수(학생이면 1, 아니면 0인 범주형 변수)로 로지스틱 회귀분석을 실시한 결과가 다음과 같다면, balance 변수만 유의수준 5%하에소 유의한 것을 확인할 수 있습니다.
다음으로 독립변수에 따른 확률값 추정을 예로 확인하기 위해 유의한 변수인 balance 변수만을 활용하여 로지스틱 분석을 실시하면 다음과 같은 결과가 나옵니다.

이를 통해 만약 balance변수가 1000$이면 아래와 같이 Default 확률을 계산할 수 있습니다.
p(X)^=1+eβ0^+β1^Xeβ0^+β1^X=1+e−10.6513+0.0055×1000e−10.6513+0.0055×1000=0.006
위 결과에 따라 만약 balance 변수가 1000$라면 0.6%의 확률로 Default가 발생함을 알 수 있습니다.
또한 만약 2000$의 값을 가진다면 다음과 같이 계산할 수 있습니다.
p(X)^=1+eβ0^+β1^Xeβ0^+β1^X=1+e−10.6513+0.0055×2000e−10.6513+0.0055×2000=0.586
따라서 이 경우에는 58.6%로 Default가 발생함을 알 수 있으며 변수는 2배 증가했지만, default 확률은 58%나 증가함을 확인할 수 있습니다.
[Geometric interpretation]
만약 2가지 변수를 통해 로지스틱 회귀분석을 한다면,
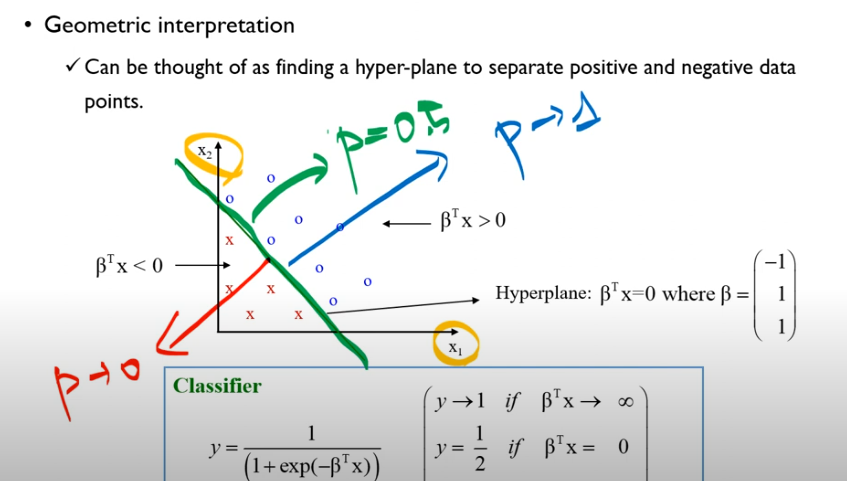
위 결과처럼 결과를 얻을 수 있습니다. 이때 만약 분류 기준이 초록색 선이라면 회귀계수에 따라 파란색 방향으로 가면 "1"로 라벨링된 범주일 확률이 1에 가까워지고 빨간색 방향에 데이터가 있을수록 확률이 0에 가까워진다는 것을 알 수 있습니다.
[Multinomial Logistic Regression]
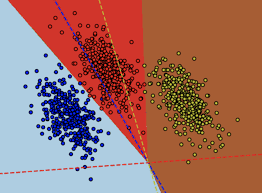
위에선 종속변수의 범주가 2개인 경우만을 살펴보았지만 범주값이 2개보다 더 많은 경우가 존재할 수 있습니다. 이 경우에는 Multinomial Logistic Regression를 통해 해결할 수 있습니다.
Multinomial Logistic Regression의 과정을 설명드리자면,
우선 일명 Baseline으로 사용할 변수를 하나 정해줍니다.
(이 글에서는 예시로 범주가 3개인 로지스틱 분석에서 y=3일 경우를 baseline으로 정해서 사용하겠습니다.)
이후 Baseline 범주를 분모로 하여 다른 범주들 각각 log(Odds)값을 통해 회귀식 2개를 계산해줍니다.
log(p(y=3)p(y=1))=β10^+β11^x1+⋯β1d^xd=β1TX
log(p(y=3)p(y=2))=β20^+β21^x1+⋯β2d^xd=β2TX
이때 위에서 살펴본 이항 로지스틱 회귀분석에서 1−pp=p(y=0)p(y=1)인 점을 생각하면 이 과정을 이해하기가 쉬울겁니다.
다음으로 위 과정을 통해 얻은 회귀식은 아래와 같이 표기할 수 있습니다.
p(y=3)p(y=1)=eβ1TX, p(y=3)p(y=2)=eβ2TX
이때 각 범주가 될 변수의 확률들을 합하면 1이 되어야 하므로
p(y=1)+p(y=2)+p(y=3)=1라는 식을 만족해야하고 이는 위 두 식을 통해 다음과 같이 나타낼 수 있습니다.
eβ1TX×p(y=3)+eβ2TX×p(y=3)+p(y=3)=1∴p(y=3)=1+eβ1TX+eβ2TX1
정리하면 종속변수가 K개의 범주로 구성되어 있을 때 K-1개의 로지스틱 회귀식을 얻을 수 있고, 이를 통해 위와 같이 다항 로지스틱 회귀식을 얻을 수 있다는 것입니다.
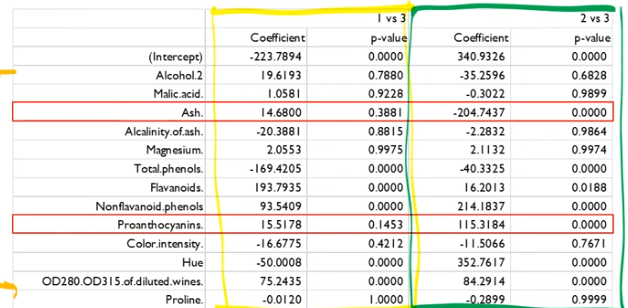
또한 범주가 3개인 다항 로지스틱 회귀분석을 실시하면 위와 같은 결과를 얻을 수 있고 결과를 살펴보면 Baseline인 "3"범주에 대해 1 vs 3, 2 vs 3으로 비교할 수 있음을 확인할 수 있습니다.
이때 중요한 점은 Ash 변수나 Proanthocyannins 변수와 같이 "1" 범주와 "3" 범주를 판단할 때는 두 변수 모두 p−value가 0.05 이상으로 유의수준 5% 이내에서 유의하지 않은 변수이지만 "2" 범주와 "3" 범주를 판단할 때는 p−value가 0에 가까운 변수로 매우 유의한 변수임을 확인할 수 있습니다.
따라서 범주 각각을 판단할 때 중요한 변수가 달라질 수 있다는 점을 유의하면 다항 로지스틱 분석을 잘 활용할 수 있을 것이라고 기대됩니다.