[DSBA-ITS504] Multiple Linear Regression

Do ·2024년 7월 9일

DSBA-ITS504 Business Analytics

목록 보기

3/6

이번 시리즈는 고려대학교 산업경영공학부 강필성 교수님의 강의를 참고하였습니다. Business Analytics라는 과목이고, 데이터사이언스 분야의 내용이 잘 정리되어 있어 공부하기 좋을 것 같아 이번 시리즈를 연재하게 되었습니다. 부족한 점이 많겠지만 데이터사이언스 공부를 하는데 도움이 되었으면 합니다.

[Multiple linear Regression]

다중회귀분석은 독립변수 $x_i$ 가 여러 개인 회귀분석을 의미합니다.
이는 다음과 같은 식으로 나타낼 수 있습니다.

y = \beta_0 \ + \ \beta_1 x_1 \ + \ \beta_2x_2 \cdots + \beta_d x_d + \epsilon \quad \cdots \ (1)

위 식에서 $\beta$ (베타, coefficient)는 개별 독립변수가 종속변수인 $y$ 에 미치는 단위당 영향력을 의미합니다. 즉 $x_1$ 한 단위가 증가할 때, 종속변수 $y$ 는 $\beta_1$ 만큼 증가한다는 것을 의미합니다.

또한 $\epsilon$ 은 noise 즉, 설명할 수 없는(unexplained) 오차를 의미합니다.

y = \hat{\beta_0} \ + \ \hat{\beta_1} x_1 \ + \ \hat{\beta_2}x_2 \dots + \hat{\beta_d} x_d \quad \cdots \ (2)

(2)번 식은 (1)번 식과 유사해보이지만 $\epsilon$ 이 없는 것을 확인할 수 있습니다. (2)번 식은 데이터를 통해 추정한 회귀 모델의 추정식입니다. 이때 (^)기호는 해당 값에 대한 추정을 의미합니다.

Explanatory Vs Predictive

회귀분석은 분석의 목적에 따라 그 용도가 나뉩니다.

독립변수와 종속변수 간 관계에 대한 설명이 중요한 경우,

Model Goal) 모델 Fit & 모델에서 각 설명변수의 영향력 파악

위와 같은 목표를 가지기 때문에

"goodness of fit"을 확인하기 위해 $R^2$ 의 크기가 중요하고, 또한 각 설명변수의 영향력을 의미하는 $\beta$ 를 눈여겨봐야 합니다.

반면, 독립변수로 종속변수를 예측하는 것이 목적인 경우,

Model Goal) Optimize Predictive accuracy

위와 같은 목적을 가지기 때문에

Train Data로만 모델을 학습시켜야 하며, 평가지표로 MSE, MAE, RMSE 등을 고려해볼 수 있습니다. 이때는 산출해야하는 Y가 가장 중요한 분석 목적이 됩니다.

회귀분석의 유형

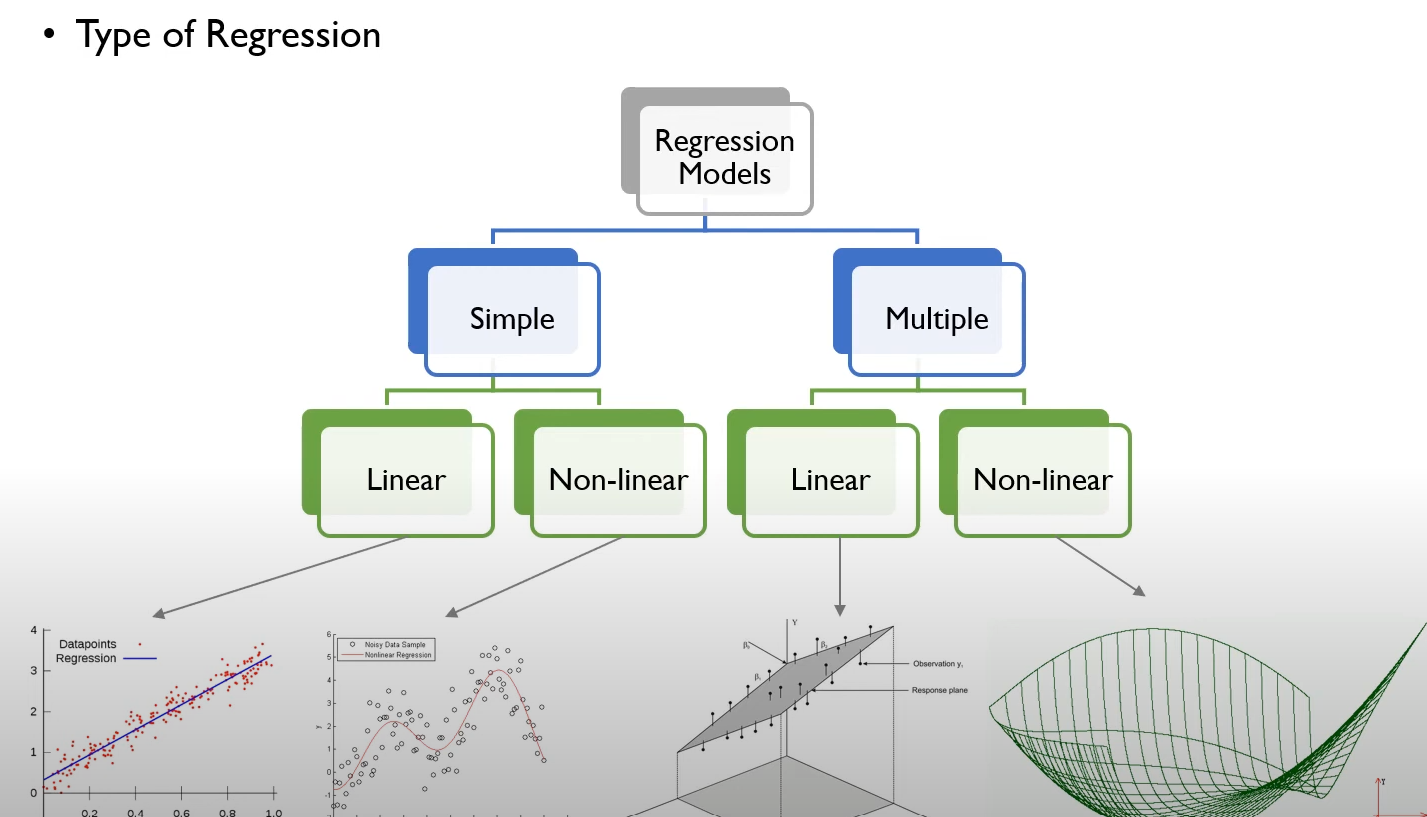
회귀의 유형은 위와 같이 나눠집니다.

독립변수의 개수가 1개일 경우 Simple Regression이라고 하며, 2개 이상일 경우 Multiple Regression이라고 합니다. 또한 $y=f(x)$ 에서 $f(x)$ 에서 선형성을 가정하면 linear, 비선형성을 가정하면 Non-linear라고 합니다.

Ordinary least square(OLS)

(2)번 식에서 독립변수로 종속변수를 알맞게 예측하기 위해 베타를 추정해줘야합니다. 이때 베타를 추정해주는 가장 일반적인 방법이 바로 OLS입니다.

OLS란 베타 계수를 추정할 때, observed value( $y$ ) 즉, 참값과 Predicted value( $\hat{y}$ )의 차이에 대한 제곱합을 최소화하는 베타로 추정하는 방법입니다.

이는 다음과 같은 식으로 표현됩니다. (이때 $\frac{1}{2}$ 는 OLS에서 $\hat{\beta}$ 를 계산하기 위해 미분 시 2를 제거하여 식을 간단하게 하기 위함으로, 뒷부분에서 다룰 예정입니다.)

min \ \frac{1}{2}\displaystyle\sum_{i=1}^{n}(y_i -\hat{y_i})^2 = \frac{1}{2}(y_i-(\hat{\beta_0} \ + \ \hat{\beta_1} x_1 \ + \ \hat{\beta_2}x_2 \dots + \hat{\beta_n} x_n))^2

머신러닝에 대한 이해를 위해 위 식을 행렬의 관점에서도 표현하면 아래와 같은 식으로 표현됩니다.

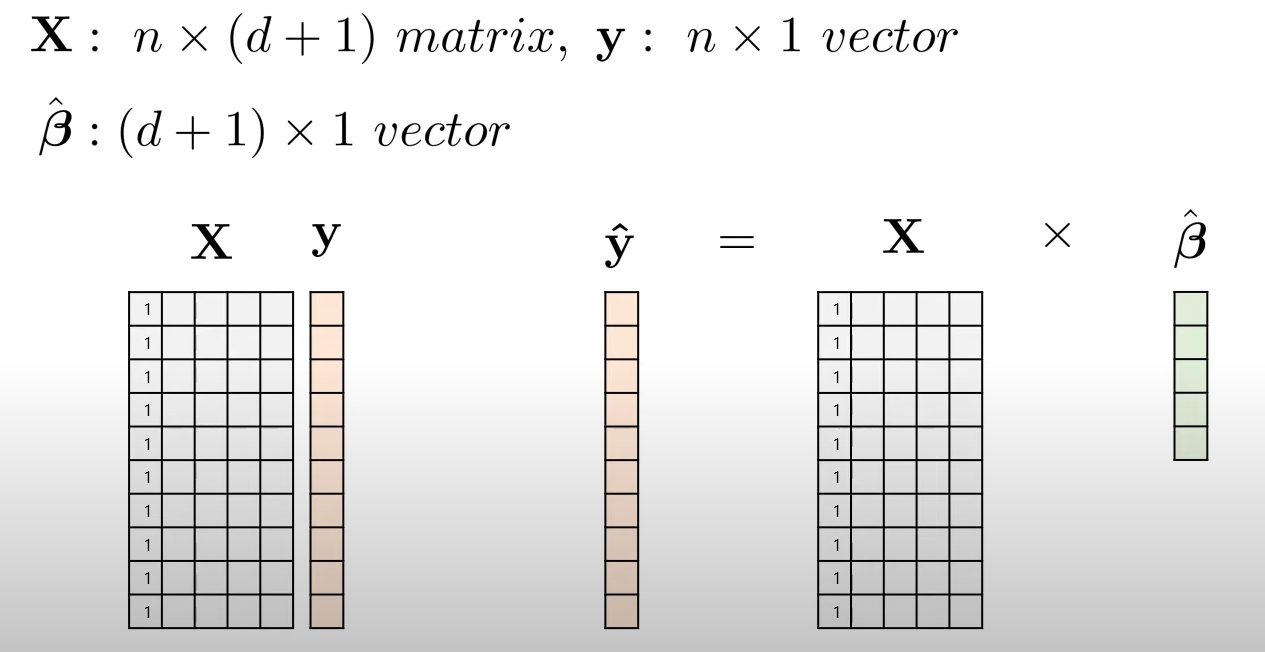
이때 $X$ 의 첫번째 열은 모두 1로 구성되어 있는 것을 확인할 수 있는데, 이는 $\beta_0$ 은 $X$ 를 곱하지 않는 상수항이기 때문에 1로 표현해주는 것입니다.

이를 미루어보아 $X$ 가 $d+1$ 개의 열을 가지는 이유도 $d$ 개의 독립변수와 1개의 상수항을 의미하는 것임을 알 수 있습니다.

이에 따라 행렬식으로 표현하면,

min \ E(X) = \frac{1}{2}(y-X\hat{\beta})^T(y- X\hat{\beta}) \\\Rightarrow \frac{\partial E(X)}{\partial \hat{\beta}} = -X^T(y-X\hat{\beta}) = 0 \\ \Rightarrow X^Ty + X^TX\hat{\beta} = 0 \\

이를 정리하면 $\hat{\beta}$ 는 다음과 같이 구해집니다.

\therefore \hat{\beta} = (X^TX)^{-1}X^Ty

위 식의 첫번째 줄에서 $y$ 와 $X\hat{\beta}$ 은 모두 $n \times 1$ 이므로 $(1 \times n)(n \times 1) = 1\times1$ 로 계산됩니다.

또한 위 식에서 $X$ 와 $y$ 는 모두 데이터에서 구할 수 있는 정해진 수이고, $\hat{\beta}$ 이 위 식에서 구해야하는 미지수이므로 $min \ E(X)$ 을 찾기 위해 $\hat{\beta}$ 으로 편미분하면 위와 같은 방법으로 $\hat{\beta}$ 을 구할 수 있습니다.

이때 이 $\hat{\beta}$ 은 unique & explict solution입니다.

이게 당연한 거라고 생각할 수 있지만 딥러닝에서는 모두 틀린 게 아닌 여러개의 정답이 나올 수 있습니다. 그런 점에서 "unique & explict solution exists!"는 큰 의의가 있습니다. 이는 나중에 딥러닝을 다루면서 다시한번 다뤄보겠습니다.

또한 이 $\hat{\beta}$ 은 Closed form Solution을 가진다는 것 역시 OLS의 가장 큰 특징입니다.

Closed form Solution $=$ analytic Solution
$\Rightarrow$ 정확한 해를 구할 수 있음
Analytical Solution (해석해) - 정확한 해를 구할 수 있음.
Numerical Solution (수치해) - 근사치를 구함. $\to$ MCMC와 연관

$\beta$ 가 best estimation이기 위해선 몇가지 가정이 필요합니다.

1) noise $\epsilon$ 가 정규분포를 따른다. $\to$ QQ-plot으로 점검가능
2) 독립변수와 종속변수 간 선형성이 있어야한다.
3) 독립변수들이 독립이어야한다.
4) noise $\epsilon$ 가 등분산성이어야한다. $\to$ 잔차 plot에서 추세가 없어야하며, 동일하게 퍼져있어야 한다.

이때 2)와 3)은 현실에서 파악하기 어렵기때문에 머신러닝 관점에서는 엄밀하게 가정을 지키지 않는다.

Goodness of fit

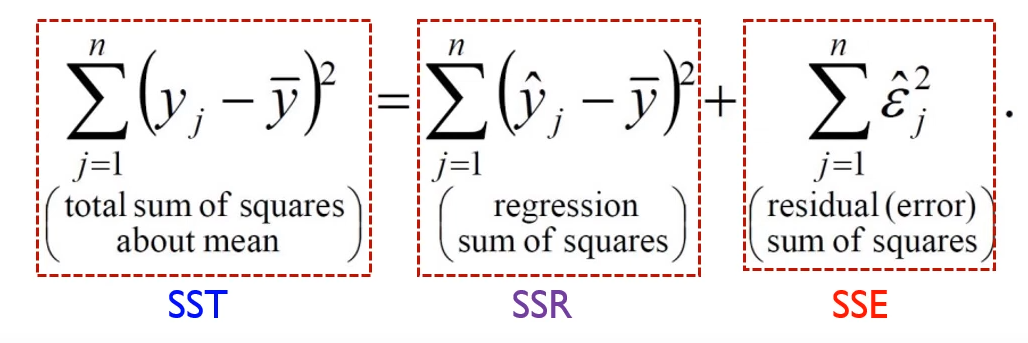
각 용어에 대해 우선 설명하자면,
$i$ 번째 실제값을 $y_i$ , $i$ 번째 예측값을 $\hat{ y_i}$ , $y_i$ 들의 평균을 $\bar{y}$ 라고 표현할 때

SST = \sum (y_i - \bar{y})^2 \\ SSR = \sum (\hat{ y_i} - \bar{y})^2 \\ SSE = \sum(y_i - \hat{ y_i})^2 \\ \\ \therefore \ SST = SSR + SSE

위와 같은 식으로 표현됩니다.

SST는 실제 y값과 y값 평균의 차이로 총변동을 의미하고, SSR은 설명가능한 수치로 y값의 평균과 y 예측값의 차이를 의미합니다. 마지막으로 SSE는 설명 불가능한 수치로 실제 y값과 y값의 예측치를 의미합니다.

OLS 관점에서는 설명이 불가능한 수치인 SSE를 작게 하는게 목적입니다. 이때 SST는 언제나 동일하므로 SSR은 크게, SSE는 작게하는 게 OLS의 목표입니다.

그리고 이 관점에서 모델의 goodness를 평가하는 방법이 바로 $R^2$ 입니다. $R^2$ 식은 다음과 같습니다.

R^2 = 1-(\frac{SSE}{SST})=(\frac{SSR}{SST})

식을 통해 $R^2$ 는 전체 변동성에서 설명할 수 있는 부분의 비율을 의미합니다.

이떄 $R^2=0$ 은 Y와 X간에 선형적인 관계가 없다는 것을 의미합니다. 즉, 비선형 관계는 있을 수 있다는 의미입니다. 그래서 단순히 분석을 할때 상관관계나 $R^2$ 만 보는 것이 아니라, 산점도 등 다양한 방식으로 Data들을 훑어봐야합니다.

또한 $R^2$ 는 변수의 수가 증가할 때 단조증가하는 경향을 보입니다. 다른말로, 의미없는 변수라도 그 수가 늘어난다면 $R^2$ 역시 계속 증가한다는 의미입니다.

이에 나온 것이 $Adjusted \ R^2$ 입니다. 식은 다음과 같습니다.

R^2_{adj} = 1-[\frac{n-1}{n-(p+1)}]\frac{SSE}{SST} \leq 1-\frac{SSE}{SST} = R^2

이때 $n$ 은 데이터의 수, $p$ 는 변수의 수를 의미합니다.

따라서, $Adjusted \ R^2$ 은 변수가 의미가 있을 때만 증가함을 알 수 있습니다.

또한, 모델이 다음 가정을 따르는지 확인해줘야 합니다.

1) Residuals are independent
2) Residuals have zero mean and a constant variance

Data Preprocessing

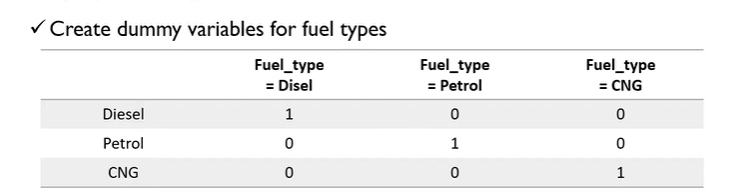
만약 회귀분석에 사용하는 변수가 위와 같이 Disel, Petrol, CNG로 나눠지는 범주형 변수라면 알맞게 전처리를 해줘야합니다. 하지만 위와 같이 한다면 CNG = 1-Disel-Petrol 이라는 식으로 계산되어 다중공선성이 발생할 수 있습니다. 따라서 Disel과 Petrol 여부 등 변수 두 개만 독립변수로 사용해야합니다. 예시는 다음과 같습니다.

회귀분석의 결과는 위와 같이 도출됩니다.

이때 p-value는 $H_0: \hat{\beta_i} = 0$ Vs $H_1: \hat{\beta_i} \neq 0$ 로 가설검정을 한 유의확률을 의미합니다.

또한 $\beta$ 는 독립변수가 1 증가할 때, 종속변수의 증가량을 의미합니다. 이때, p-Value가 유의미하다(일반적으로 0.05이하)면 $\beta$ 값이 의미가 있어집니다.

[회귀분석의 평가지표]

1. Average Error

\frac{1}{n}\sum^{n}_{i=1}(y_i-y'_i)

평균 오차는 말그대로 실제값과 예측값의 차이를 평균한 값을 의미합니다.
하지만, 부호의 효과를 제대로 도출할 수 없기 때문에 이는 좋은 평가지표라고 할 수 없다.

그래서 이러한 문제를 해결하기 위해 나온 평가지표들이 아래 평가지표들이다.

2. Mean Absolute Error (MAE)

\frac{1}{n}\sum^{n}_{i=1}\vert y_i-y'_i\vert

하지만 평균절대오차 역시 단점을 가지고 있습니다.
바로 Y의 Scale과 상관없이 Mae의 결과가 똑같이 도출된다는 뜻입니다.

예를 들어 y가 100, y'이 101이여도 MAE는 1이고 y가 1, y'이 0일 때도 MAE는 1로 똑같은 값을 가진다는 의미입니다.

그래서 이를 보완하기 위해 등장한 것이 바로 MAPE입니다.

3. Mean Absolute Percentage Error (MAPE)

\frac{1}{n}\sum^{n}_{i=1}\vert \frac{y_i-y'_i}{y_i}\vert

4. Mean Squared Error(MSE) & 5. Root Mean Squared Error(RMSE)

MSE = \frac{1}{n}\sum^{n}_{i=1}(y_i-y'_i)^2, \ RMSE = \sqrt{\frac{1}{n}\sum^{n}_{i=1}(y_i-y'_i)^2}

MAE와 같이 절댓값을 씌우는 평가지표의 경우 실무자들이 직관적으로 이해하기 쉽지만, 미분불가능한 부분이 있을 수 있기 때문에 연구에서 평가지표는 MSE와 같이 제곱의 형태로 부호의 효과를 보완시키는 방법을 사용합니다.

공부하는 사람

이전 포스트

[DSBA-ITS504] Introduction - Machine Learning

다음 포스트