이번 시리즈는 Ian Goodfellow, Yoshua Bengio와 같은 세계적인 석학들이 집필하신 Deep learning(2017, MIT)를 읽어보며, 이를 기록하고자 시작하게 되었습니다. 부족한 점이 많더라도 양해를 구합니다.

[Point]

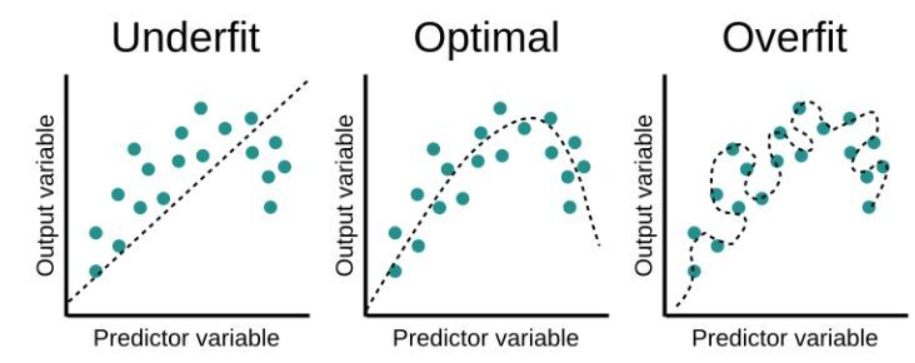
머신러닝에서 중요한 문제 중 하나는 "Train data뿐만 아니라 Test data에서도 모델의 성능이 좋아야 하는 것입니다.

만약 Train에선 너무 좋지만 test에서 좋지 못하다면 이는 General한 모델이 아니라고 할 수 있습니다. 이런 문제를 과적합이라고 합니다.

그래서 이번 단원에선 이 과적합 문제를 해결하는 방안에 대해 다루고자 합니다. 이때 그 해결방안을 바로 Regularization(규제화)라고 합니다.

Deep learning에선 규제화를 다음과 같이 정의합니다.

"any modification we make to a learning algorithm that is intended to reduce its generalization error but not its training error."

즉, training error가 증가하더라도 일반화 에러를 줄이는 방법을 의미합니다.

[L1 & L2 규제]

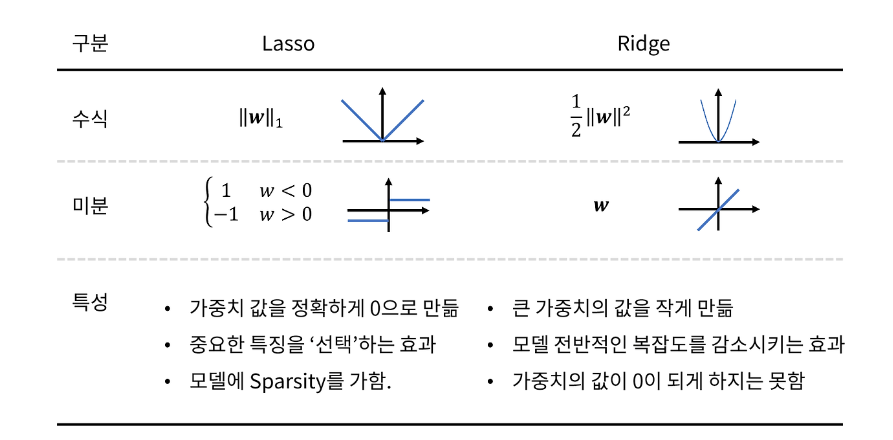
첫번째 규제화 방법은 Lasso라고도 하는 L1 규제와 Ridge라고 하는 L2 규제입니다.

우리는 모델을 만들 때 Train data만 사용하기 때문에 모델이 과적합된다면 Train data의 특징이 과하게 모델에 반영되어 손실함수가 필요이상으로 작아져버릴 수 있습니다.

따라서, 이 방법은 Cost 항에 규제항을 더하는 방법입니다. 이때 이 규제항은 모델에서 사용되는 가중치 $W_i$가 포함되어 있습니다.

그리고 모든 모델 알고리즘은 Cost function을 감소시키는 방안으로 작동하기 때문에 그 과정에서 규제항의 가중치 역시 감소되기 때문에 해당 방법이 규제화의 효과가 있다고 할 수 있습니다.

[Norm]

규제식을 살펴보기 전 우린, Lp Norm의 개념을 알아둬야합니다.
Norm은 유한차원의 벡터공간에서 백터간 거리를 의미합니다.
이때 Lp Norm 수식은 다음과 같이 정의됩니다.

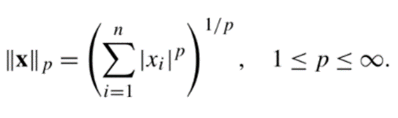
위 수식에서 n과 p는 실수이며, p는 norm의 차수, n은 벡터의 차원 수를 의미합니다. P의 차수에 따라 Norm은 다음과 같은 특징을 가집니다.

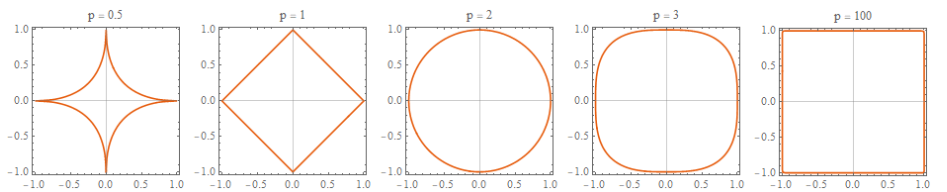
위 그림을 살펴보면 L1의 분포는 마름모꼴, L2는 원, P가 커질수록 정사각형의 모습을 가지는 것을 알 수 있습니다.

따라서 Norm 중 형태의 특수성을 가지는 L1 Norm, L2 Norm, L$^\infty$ Norm을 많이 사용합니다.

[L1]

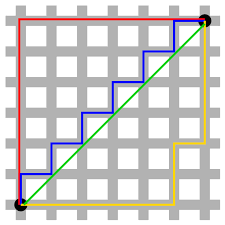
L1 Norm(Manhattan distance, 맨해튼 거리)는 다음과 같이 택시가 블록 사이사이를 이동하는 것과 같은 거리를 의미합니다.

L1 loss는 아래 수식과 같이 실제값과 예측값 오차에 대한 절대값을 찾는 방법입니다. 즉, 평가기준 중 Mae와 관련있다고 할 수 있습니다.

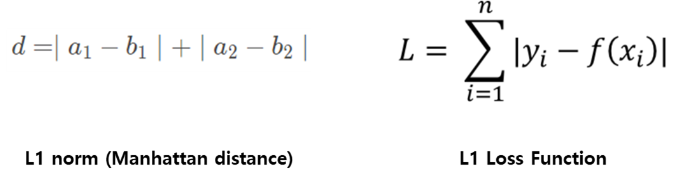
따라서 이와 관련된 L1 규제(Lasso)부터 살펴보면,

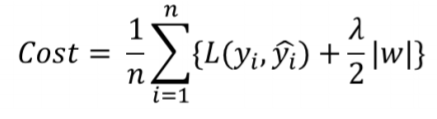
다음과 같은 비용함수를 가지며 이는 L1 loss function에 L1 Norm을 더한 식과 같습니다. 또한 위 식의 $\lambda$는 규제의 양을 적용하는 파라미터입니다.

이를 $W_i$로 편미분하면 다음과 같은 식입니다.

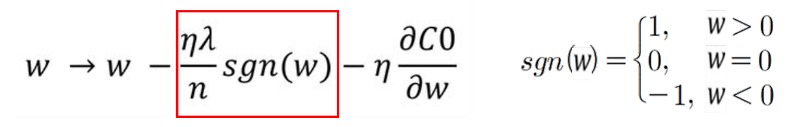
위 식을 통해 Weight의 크기에 상관없이 부호에 따라 일정한 상수 값을 빼거나 더해주게 됩니다. 따라서 특정 Weight를 0으로 만들어주는 feature selection 효과를 가지게 됩니다. 이를 통해 특정 가중치를 삭제해 모델의 복잡도를 낮출 수 있습니다.

[L2]

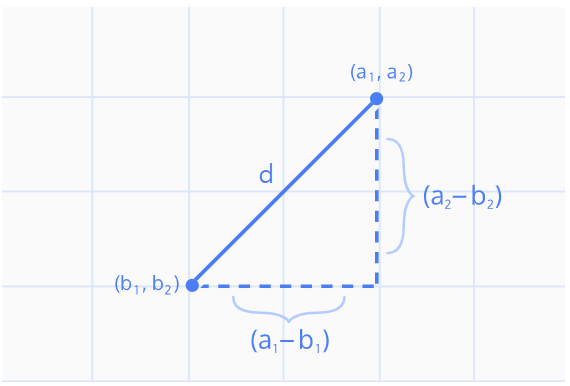
L2 norm은 유클리드 거리라고 하며, 두 점 사이의 최단 거리를 측정하는데 자주 사용됩니다. 수학에서 두 점 사이의 거리를 구하는 해당 방식으로 많은 알고리즘들이 작동하고 있습니다.

또한, L2 loss는 실제값과 예측값의 제곱합으로 나타납니다.

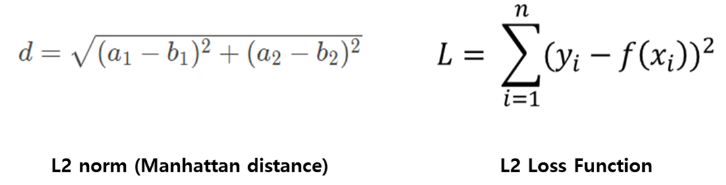
따라서 이와 관련된 L2 규제(Ridge)를 살펴보면,

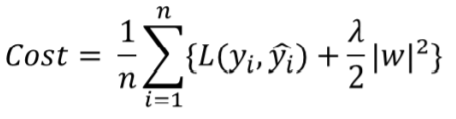
다음과 같이 L2 loss function에 L2 Norm을 더한 식과 같은 Cost function을 사용합니다. 또한 위 식의 $\lambda$는 규제의 양을 적용하는 파라미터입니다. 그리고 이를 $W_i$로 편미분하면 다음과 같은 식이 얻어집니다.

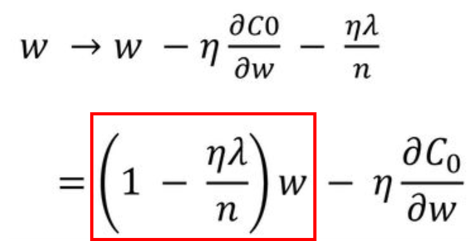
제곱을 미분할 경우 $W_i$가 사라지지 않으므로, 변수선택의 효과는 L1에 비해 없지만, Weight 크기에 따라 Weight값이 큰 값을 더 빠르게 감소시키는 가중치 감쇠 효과가 있습니다.

Weight의 크기에 따라 가중치의 패널티 정도가 달라지기 때문에 가중치가 전반적으로 작아져서, 학습효과가 L1 대비 더 좋게 나타납니다.

[L1, L2 정리]

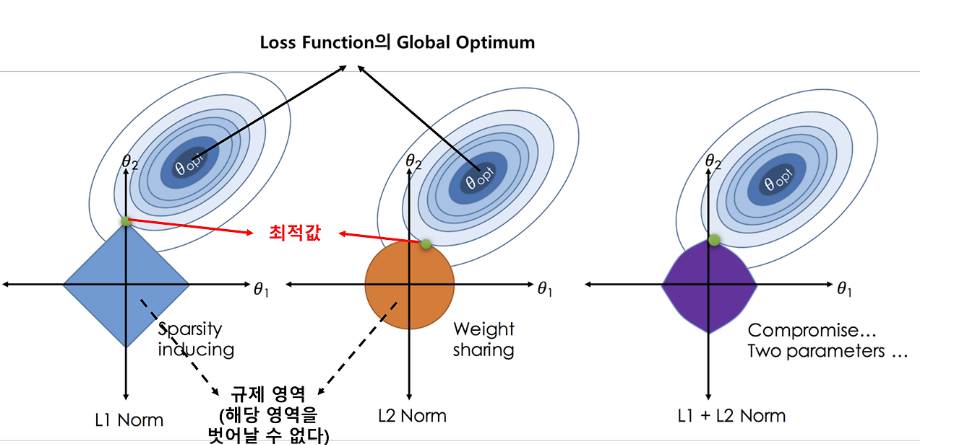
그래프로써 이를 이해해보면, L1 규제의 경우 기하학적 특성상 규제영역의 꼭짓점에서 최적값을 얻는 경우가 많고, 그렇기 때문에 변수가 선택되는 특징을 가지고 있습니다. 반면 L2 규제의 경우 원과 접점에서 최적값을 얻기 때문에 L1에서 가중치가 0이 되는 상황이 많이 발생하게 되는 것입니다.

해당 단원을 정리하면 다음과 같습니다.

• 출처: https://seongyun-dev.tistory.com/52

[Data Augmentation]

모델에서 과적합을 방지하는 또다른 방법은 데이터 증강입니다.

모델은 데이터의 양이 적을 경우 해당 데이터의 특정 패턴이나 노이즈까지 학습하기 때문에 과적합이 발생합니다. 따라서 데이터의 양을 늘려서 일반적인 패턴을 학습하도록 할 수 있습니다.

하지만 만약, 데이터를 추가적으로 얻을 수 없다면??

이때 사용되는 방법이 Data Augmentation(데이터 증강)입니다.

데이터 증강이란 원본 데이터로부터 새로운 데이터를 만들어내는 것을 말하며 데이터 증강은 사용하는 데이터의 종류에 따라 특성이 달라집니다.

[이미지 데이터]

1) Flipping

이 기능은 이미지를 대칭이동하는 방법입이다. 한 가지 주의할 점은 숫자나 알파벳 문자를 인식하는 경우에는 b와 d 같이 대칭되는 문자로 잘못 인식할 수 있다는 것입니다. 이를 주의하면서 사용해야 합니다.

2) rotation

이는 이미지 데이터의 각도를 다르게 하는 방법입니다.

3) shifting

이 방법은 이미지 데이터를 이동시켜 새로운 데이터를 만들어내는 방법입니다.

4) Gray Scale

Gray scale은 3가지 채널(channel)을 가지는 RGB 이미지를 하나의 채널만을 가지도록 해서 새로운 데이터를 만드는 방식입니다.

5) Saturation

Saturation은 RGB 이미지를 HSV, 즉 Hue(색조), Saturation(채도), Value(명도)의 3가지 성분으로 색을 표현하는 것을 통해 이미지로 변경하고 S(Saturation) 채널에 오프셋(offset)을 적용, 조금 더 이미지를 선명하게 만들어 주고 다시 우리가 사용하는 RGB 색상 모델로 변경하여 새로운 데이터를 만들어내는 방법입니다.

색상에 대해서 살짝 정리를 하고 넘어가면 좋을 것 같아서, 잘 설명된 글을 가지고 와봤습니다.

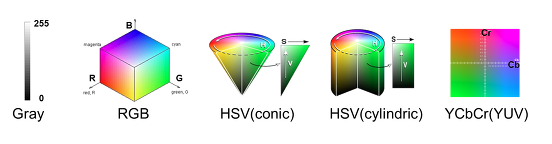
Gray 모델 : 색(Color) 정보를 사용하지 않고, 밝기 정보만으로 영상을 표현하는 것. 검정(0)부터 흰색(255) 까지 총 256단계의 밝기 값으로 픽셀 값을 표현한다.

RGB 모델 : 가장 기본적인 색상 모델로, 색을 Red, Green, Blue의 3가지 성분의 조합으로 생각하는 것을 말한다. RGB 모델에서는 색상에 관하여 다음과 같이 픽셀값을 가지므로 참고 바란다.

검은색은 R,G,B의 값이 모두 0 -> (0,0,0)
흰색은 R,G,B의 값이 모두 255 -> (255,255,255)
빨간색은 R이 255, 나머지 G,B가 0 -> (255,0,0)
초록색은 G가 255, 나머지 R,B가 0 -> (0,255,0)
파란색은 B가 255, 나머지 R,G가 0 -> (0,0,255)
노란색은 R과 G가 255, B=0 -> (255,255,0)
여기서 R=G=B일 경우는 무채색인 Gray 색상을 따르게 된다. R, G, B가 각각 0~255 사이의 값을 가질 수 있으므로, RGB 색상 모델을 사용하면 총 256 X 256 X 256 = 16,777,216 가지의 색을 표현할 수 있다.

HSV 모델 : Hue(색조), Saturation(채도), Value(명도)의 3가지 성분으로 색을 표현한다. Hue의 색조란 해당 색이 붉은색 계열인지 푸른색 계열인지를 나타내고, Saturation의 채도란 해당 색이 얼마나 선명하고 순수한 색인지, Value의 명도란 밝기(Intensity)를 나타낸다.

HSV 모델은 우리가 색을 가장 직관적으로 표현할 수 있는 모델이고, 머릿속에서 상상하는 색을 가장 쉽게 만들어낼 수 있는 모델이다. 영상처리 / 이미지 처리에서 HSV 모델을 사용할 때, H, S, V 각각은 0~255 사이의 값으로 표현된다. H 값은 색의 종류를 나타내기에 크기가 의미가 없이 단순 인덱스를 나타내는 것이며, S 값은 0이면 무채색(gray색), 255면 가장 선명한(순수한) 색임을 나타낸다. V 값은 작을수록 어둡고, 클수록 밝은 색임을 나타낸다. HSV 색상 모델은 그림과 같이 원뿔(conic) 형태, 원기둥(cylindric) 형태가 있다.

YCbCr 모델 : RGB 색에서 밝기 성분과 색차 정보를 분리하여 표현하는 색상 모델이다. 디지털 영상에서 Y, Cb, Cr은 각각 0~255 사이의 값을 가지며, Y가 커지면 그림이 전체적으로 밝아지고, Y가 작아지면 전체적으로 어두워진다. YCCr 모델은 mpeg에서 사용되는 색상모델로써, 인간의 눈이 밝기 차에는 민감하지만, 색차에는 상대적으로 둔감하다는 점을 이용해서 Y에서 많은 비트수(해상도)를 할당하고, Cb, Cr에는 낮은 비트 수를 할당하는 방식으로 비디오를 압축한다. 따라서 비디오 데이터를 처리할 경우에 YCbCr 모델을 사용하면 별도의 색상 변환을 하지 않아도 되는 장점이 있다. 참고로 YCbCr 모델은 YUV 모델로도 불린다

6) Brightness

이는 밝기를 조절해서 새로운 데이터를 얻는 방법입니다.

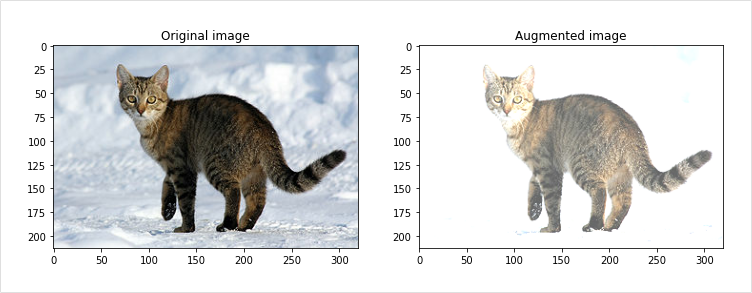
7) Center Crop

이 방법은 이미지의 중앙을 기준으로 확대하는 방법입니다. 하지만 이때 너무 작게 center crop을 할 경우 본래 가진 라벨과 맞지 않게 되는 상황이 발생할 수 있으니 주의가 필요합니다.

8) Noise 추가

소금과 같이 하얀 점을 이미지 데이터에 추가하거나 후추와 같이 검은 점을 데이터에 임의로 흩뿌려서 새로운 데이터를 만들어내는 방법입니다.

[텍스트 데이터]

텍스트의 경우에도 노이즈를 추가하는 방식을 통해 데이터를 확장 및 증강할 수 있습니다. 다만 자연어 문장의 경우 생각보다 어순 변화나 단어의 변화에 민감하기 때문에 생각처럼 잘 동작하지 않을 수 있습니다.

또한 규칙에 의해서 문장을 변형할 경우, 규칙 자체를 신경망이 학습할 수 있기 때문에 위험할 수 있습니다. 따라서 이미지만큼 쉽게 데이터를 증강할 수는 없지만, 종종 다음과 같은 방법을 통해 데이터를 증강합니다.

1) 단어의 생략

다음 그림과 같이 임의로 일정 확률로 단어를 생략하는 것입니다. 참고로 실제로는 빈 칸을 텍스트로 넣어주는게 아니라, 해당 단어가 빠진 채로 문장이 들어가게 됩니다. 만약 생략 확률이 너무 높다면 문장의 의미가 왜곡될 가능성이 높아지고, 생략 확률이 낮다면 단어 증강의 효과가 줄어들 것입니다

2) 단어 교환

다음 그림과 같이 임의로 일정 윈도우(window) 내에서 단어를 교환하는 것입니다. 예를 들어 다음 그림과 같이 ‘학교에’라는 단어를 앞뒤 3단어까지의 범위 내에서 임의의 단어를 선택하여 교환하는 것입니다.

3) 단어 이동
다음 그림과 같이 임의로 일정 윈도우 내에서 단어를 이동하는 것입니다. 교환보다는 조금 더 공격적인 방법입니다.

한국어는 교착어에 속하며 어순에 제한받지 않기 때문에, 이러한 단어의 교환 및 이동 등은 한국어의 경우 훨씬 더 잘 동작할 수 있습니다. 따라서 일부 언어에서는 이에 비해 훨씬 제한적일 수 있으므로, 언어에 대한 면밀한 고찰이 수행된 이후에 데이터 증강 작업이 수행할 필요가 있습니다.

참고로, 위 방법 중 임의의 단어를 삽입 or 삭제하는 방법과 문장내 두 단어의 위치를 임의로 바꾸는 방법이 원본 문장의 라벨을 대체로 잘 따른다는 결과가 있습니다.

[시계열 데이터]

시계열 데이터란, 일정 시간 간격으로 배치된 데이터들을 말합니다.

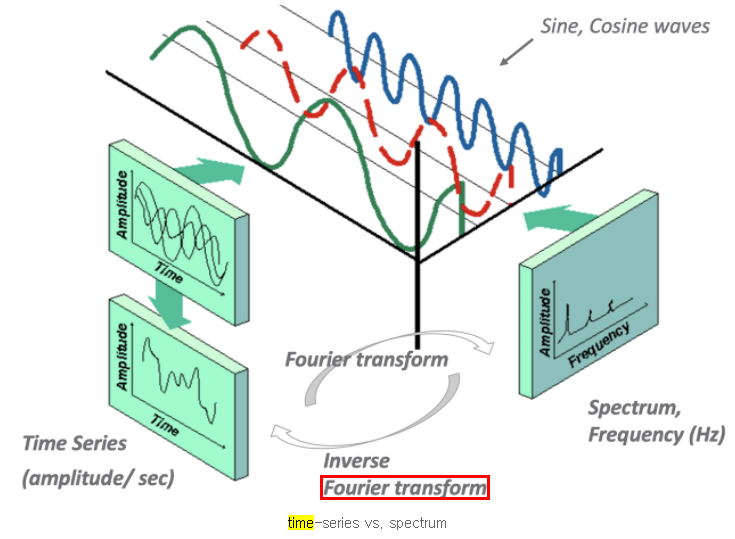
시계열 데이터는 다음과 같이 시간 영역과 주파수 영역으로 나누어 분석할 수 있습니다.

시간 영역 (time domain)
일정 기간 동안의 데이터를 분석하는 것 ( = 변수를 시간에 대해 측정)
ex. 시간 영역에서의 전기 신호 분석 : 오실로스코프

주파수 영역 (frequency domain)
주파수에 대한 수학적 함수 또는 신호를 주파수와 관련하여 분석하는 것

푸리에 변환 (시간 영역 → 주파수 영역)
시간 도메인에서의 연속적 신호를 여러 sin 곡선들의 합으로 나타내어
주파수 도메인으로 변환할 수 있음
cf. 역 푸리에 변환 : 주파수 영역 → 시간 영역

[시계열 데이터 증강의 어려움]

시계열 데이터 증강에는 다음과 같은 어려움이 있다.

1. 현재의 데이터 증강 기법은 시간에 종속적(temporal dependency)이라는 시계열의 본질적 특성을 활용하지 못한다.
2. 증강 기법은 task에 의존적이기 때문에 ‘시계열 분류’에 적용 가능한 증강 기법이 ‘이상치 탐지’에는 적용되기 힘들 수 있다.

따라서 단순히 기존의 데이터 증강을 적용하는 것은 효과적이지 않으므로
시계열 데이터를 위한 증강 방법을 고안할 필요가 있다.

[시계열 데이터 증강의 분류]

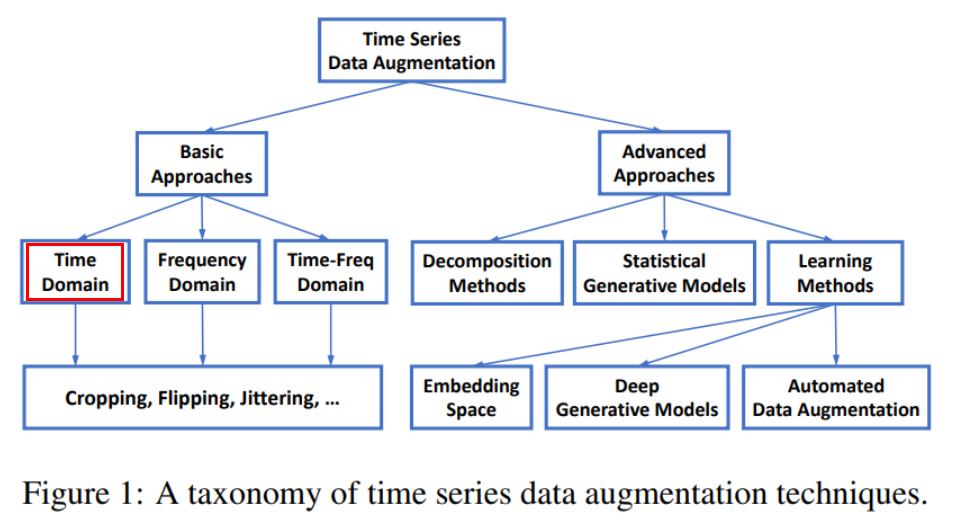
이 중 가장 활용도가 높은 Time Domain에서의 시계열 데이터 증강 기법부터 정리하자면 다음과 같은 방법들이 있습니다.

Window cropping or slicing
원본 데이터에서 랜덤하게 연속적인 slice를 추출하는 방법이다.
CV에서 이미지를 랜덤하게 잘라 데이터를 증강하는 것과 유사하다.

Window warping
랜덤한 구간을 선정하여 압축 or 확장하는 방법이다. (DTW와 유사함)
원본 시계열의 전체 길이를 바꿀 수 있다.

Flipping
원본 데이터의 부호를 바꿔 새로운 시퀀스를 만드는 방법이다.
부호를 바꿔도 라벨은 동일하다. (시계열 분류, 이상치 탐지 둘 다 해당됨)

Noise injection
라벨을 바꾸지 않은 채 원본 데이터에 노이즈를 삽입하는 방법이다.
가우시안 노이즈(정규분포를 갖는 잡음) 또는
spike, step-like trend, slope-like trend 등의 노이즈를 삽입할 수 있다.

Label expansion
이상치 감지를 위한 증강 기법이다. 시계열 데이터에서 이상치는 연속적으로 발생하기 때문에 시작점과 끝점이 모호하다. 따라서 시간 거리와 값 거리가 이상치와 가까운 데이터는 이상치일 가능성이 높다. 이러한 데이터를 이상치로 분류하여 라벨을 확장할 수 있다.

[Noise Robustness]

머신러닝에서 Robust란?
머신러닝에서 일반화(generalization)는 일부 특정 데이터만 잘 설명하는(=overfitting) 것이 아니라 범용적인 데이터도 적합한 모델을 의미합니다.

즉, 잘 일반화하기 위해서는 이상치나 노이즈가 들어와도 크게 흔들리지 않아야(=robust) 합니다.

Rubust한 모델을 방법
노이즈나 이상치(outlier) 같은 엉뚱한 데이터가 들어와도 흔들리지 않는 모델을 만들기 위한 방법으로 일부러 노이즈를 주는 방법이 있습니다.
(바이러스를 일부러 몸에 노출시켜 항체를 만드는 예방접종과 비슷한 원리)

예를 들어, 레이어 중간에 노이즈를 추가(noise injection)하는 게 파라미터를 줄이는 것(L2 weight decay)보다 강력할 수 있고,

웨이트(weight)에도 노이즈를 넣어줄 수도 있다. (히든 레이어를 드롭아웃 하는 것 보다 덜 엄격한 느낌이 든다)

만약 분류 문제의 경우 라벨을 부드럽게(label-smoothing) 하는 방법이 있다. (예: 1,0,0 -> 0.8,0.1,0.1)

[Semi-Supervised Learning]

비지도 학습과 지도 학습을 합친 것으로, 딥러닝에서는 representation을 찾는 과정이다. CNN을 생각해보면, 컨볼루션과 서브샘플링이 반복되는 과정인 특징선택(feature extraction)이 일종의 representation을 찾는 과정이다.

그렇다면 딥러닝에서 representation이란 무엇일까?

직관적으로 이해해보면,

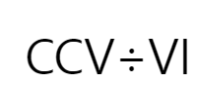
와 같은 로마자 표현과

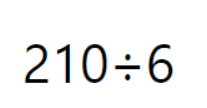
다음과 같은 아라비아 숫자 표기가 있다고 할 때 이를 나누기하라는 Task의 난이도는 어떨까요??

아라비아 숫자 표기가 훨 쉬울겁니다.

즉, "어떤 Task를 처리할 때 정보를 어떻게 가공하여 표현(representation)하는지에 따라서 task의 난이도가 결정된다는 것"입니다.

그래서 오토인코더와 차원축소의 개념과 같이 부적절하게 표현된 input을 적절하게 가공하여 representation을 하여 General한 모델을 만들 수 있습니다.

[Multi-task Learning]

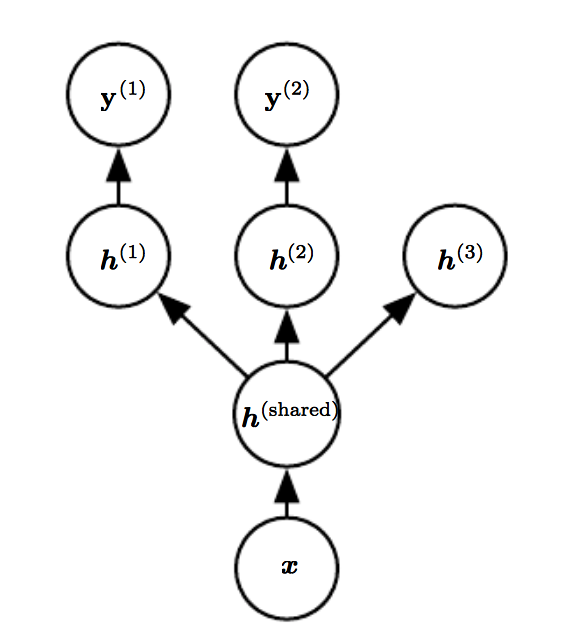
이 학습 방법은 하나의 input으로 여러 문제를 해결하는 방법입니다. 예를 들어 얼굴 이미지 데이터로 성별이랑 나이를 한번에 맞추는 문제 등이 있습니다.

Shared 구조를 덕분에 representation를 잘 찾아줍니다. 서로 다른 문제(task) 속에서 몇 가지 공통된 중요한 요인(factor)이 뽑히며, shared 구조를 통해서 representation을 찾을 수 있습니다. 모델의 앞단에 있는 shared 구조 덕분에, 각각의 요인을 학습시킬 때보다 더 좋은 성능을 낸다고 합니다.

예를 들어 최근에 Google의 NLP에서는 감정분석/번역 등 굉장히 다양한 멀티태스크러닝을 통해서 모델 성능이 좋아진다는 연구를 발표하기도 했습니다.

이때, 딥러닝 관점에서 multi-task learning을 하기 위해서는 모델의 학습셋으로 사용되는 변수는 연관된 다른 모델의 변수와 두 개 이상 공유한다는 가정이 전제되어야 한다는 점은 유의해야할 필요가 있습니다.

[Early stopping]

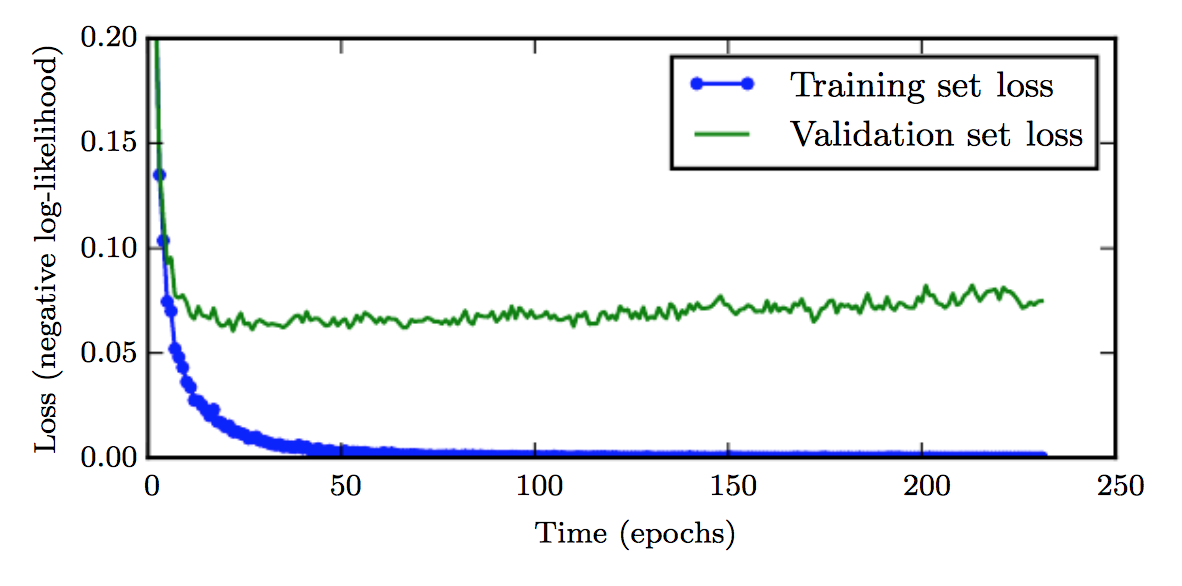
Epoch 수(학습 반복 횟수)가 늘어날수록 학습셋에 대한 오차는 줄어들지만, 검증셋의 오차가 증가하며 과적합이 발생할 수 있습니다.

따라서, 이전 에포크과 비교해서 오차가 증가하면 과적합이 발생하기 전에 학습을 멈추는 것을 'early stopping'이라고 합니다.

[Parameter Typing & Sharing]

여러 파라미터가 있을 때 몇 개의 파라미터를 공유하는 역할을 하는 것을 의미합니다. 어느 레이어의 파라미터를 공유하거나, 웨이트를 비슷하게 함으로써 각각의 네트워크에 파라미터 수를 줄어드는 효과가 있고,

이를 통해 파라미터 수가 줄어들면, 일반적인 퍼포먼스가 증가하는 효과가 있어서 모델의 성능이 좋아지는 데 도움이 됩니다.

1) Parameter Typing (파라미터 수를 줄이는 역할)
: 입력이 다른데 비슷한 작업(task)을 하는 경우 (예: MNIST, SVHN 데이터셋) 특정 레이어를 공유하거나 두 개의 웨이트를 비슷하게 만든다.
2) Parameter Sharing
: 같은 컨볼루션 필터가 전체 이미지를 모두 돌아다니면서 찍기 때문에 대표적인 예를 CNN이 있다.

[dropout]

"신경망의 일부를 사용하지 않는 방법"으로, 이는 과적합을 방지하는 효과가 있습니다.

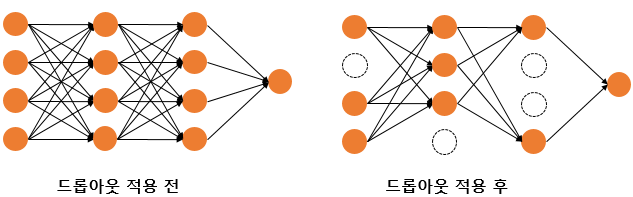
예를 들면 드롭아웃의 비율을 0.5로 한다면 학습 과정마다 랜덤의 절반 뉴런만을 사용하기 때문에 상세한 Train data들을 학습하지 않게 함으로써 과적합을 방지하는 효과가 있습니다.

드롭아웃은 신경망 학습 시에만 사용하고, 예측 시에는 사용하지 않는 것이 일반적이고 학습 시에 특정 뉴런, 특정 조합에 너무 의존적이게 되는 것을 방지해주며, 매번 랜덤 선텍으로 뉴런을 사용하지 않기에 서로 다른 신경망들을 앙상블하여 사용하는 것 같은 효과를 내어 과적합을 방지하는 효과가 있습니다.