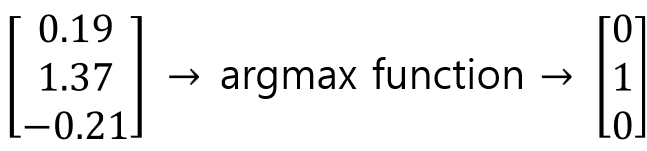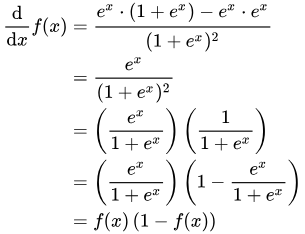이번 글에서는 앞으로 자주 다루게 될 딥러닝에 대해 개괄적으로 다뤄보도록 하겠습니다.

[Output / Loss function]

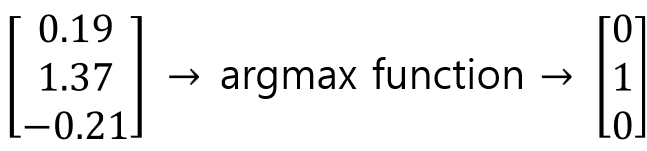
우리가 이해하기 가장 쉬운 이진분류 문제(Binary Classification)를 예시로 Output function or Loss function 에 대해서 알아보자

만약에 MLP를 활용해 모델을 구성하여 출력층에서 다음과 같이 결과가 도출되었다. 이때 MLP 결과는 우리가 원하는 0 or 1이 아니라 위 왼쪽 행렬과 같이 출력층 결과가 도출된다.

따라서 우리는 출력층 결과를 결과 값인 각 Class에 mapping 을 해야한다.

이를 위한 function으로 기존엔 argmax 값을 사용하고자 하였다.

만약에 위와 같이 출력층의 결과가 도출된다면 1.37을 class 1에 매핑했다. 하지만 이 방식은 스코어값이 천차만별로 튀어나오고 이진분류에선 크게 도움이 안된다.

왜냐면 argmax function을 사용한다면 $(1.37, 0)$이든 $(1.37, 1.36)$이든 큰 값을 1로 매칭한다는 것인데, 이는 거의 비슷한 값일 수 있음에도 0과 1로 확 구분된다는 문제점을 가지고 있기 때문이다.

즉, argmax function은 출력값 결과 자체는 비슷한데도 class가 나뉘므로 분류 성능이 낮다.

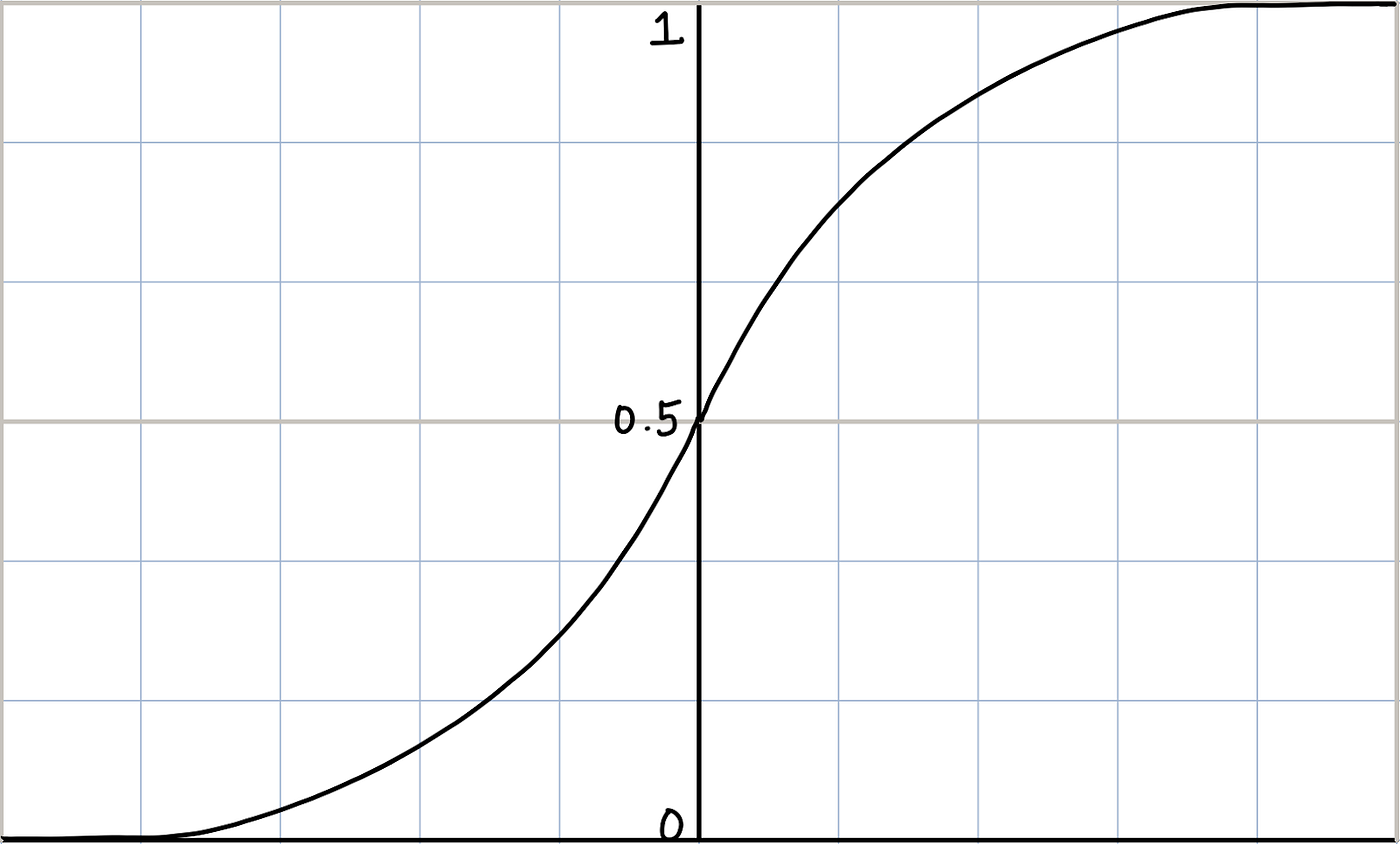
그래서 등장한 게 softmax function이다.

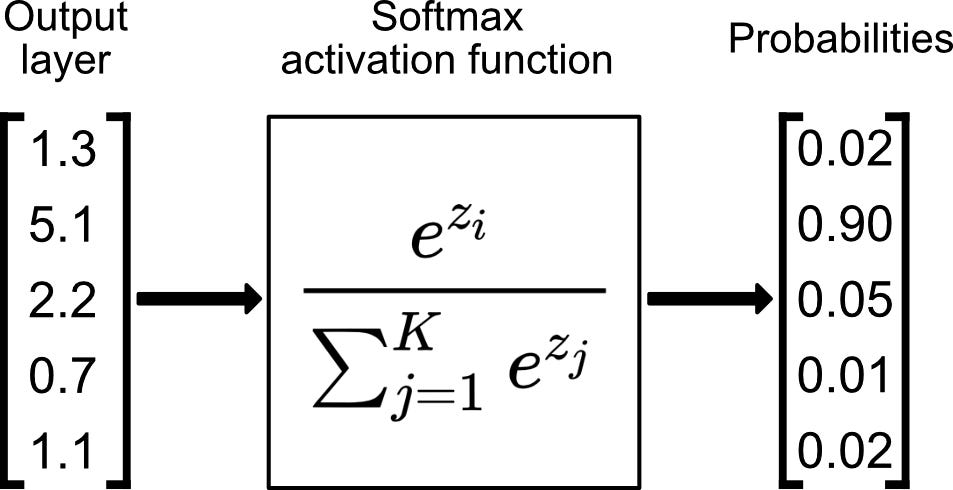
softmax function은 위와 같은 식으로 구성되며, 장점은 0과 1사이로 출력값이 나오고 이 출력값의 합이 1이 된다는 것이다.

왜냐하면 출력값의 합이 1이 되기 때문에 찾고자 하는 정답인 1과 0에 가깝게 나눠질 수 있고, Good case엔 1과 0으로 명확하게 나눠질 수도 있는 함수이기 때문이다. 따라서 실제로 Softmax function 을 많이 사용한다고 한다.

또한 결과값을 정규화시킨다는 특징이 있으며 지수함수를 사용함으로써 미분을 가능케하고, 입력값 중 큰 값은 더 크게 작은 값은 더 작게 만들어 Classification 이 더 명확해진다는 특징도 있다.

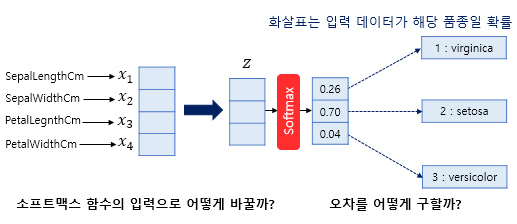
출력층에 자주 사용되는 Softmax function은 입력으로 사용되는 벡터의 차원은 분류하고자 하는 Class의 개수가 되어야 하므로 만약 위의 그림처럼 4개의 변수로 구성된 경우 4차원 벡터가 입력되는데, 이때는 어떤 가중치 연산을 통해 3차원 벡터로 바꿔줘야 한다.

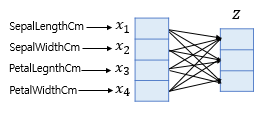
따라서 4차원 데이터 벡터를 Softmax function의 입력 벡터로 차원을 축소하려면 위와 같이 입력 벡터 $Z$의 차원수만큼 결과값이 나오도록 가중치 곱을 진행하여 위 그림처럼 총 12(3 x 4)개의 화살표가 다른 가중치를 가지며 학습 과정에서 점차적으로 오차를 최소화하는 가중치로 값이 업데이트되도록 바꿔주면 된다.

그렇다면 오차를 줄이는 방향으로 가중치를 어떻게 업데이트시키냐?

바로 Cross-entropy를 활용한다.

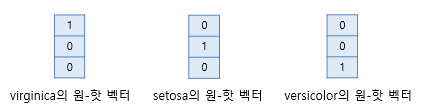
만약 위와 같이 3개의 Class가 있을 때 각 실제값마다 다음과 같은 원-핫 벡터가 존재할 것이다.

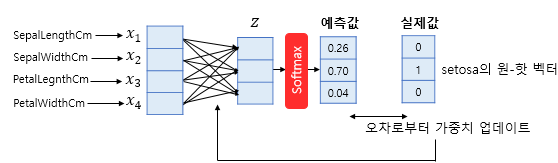
만약 데이터의 실제 Class가 setosa라면 위와 같이 setasa의 원-핫 벡터와 예측값 간의 차이를 오차로 정의하여 그 오차를 이용하여 Cross-entropy 를 손실함수로 사용하여 손실함수가 최소화되는 방향으로 가중치를 업데이트한다.

Cross-entropy는 위 식과 같이 구성되는데, 만약 3개의 클래스 $c_1, c_2, c_3$가 존재하는 분류 문제에서 어떤 데이터의 출력값이 다음과 같다면

모델이 나타내는 확률분포 $Q(x)$는 다음과 같이 나타낼 수 있다.

만약 데이터가 실제로 2번 Class에 해당한다면 데이터의 실제 확률분포 $P(x)$는 아래와 같이 나타난다.

따라서 위의 $Q(x)$와 $P(x)$를 통해 Cross-entropy를 계산한다면 다음과 같은 결과가 도출된다.

이때 $H(P,Q)$를 최소로 만들도록 가중치를 업데이트한다.

예를 들어 $Q(x)$가 $[0.4, 0.4, 0.2]$라면 $H(P,Q)$값이 더 커지게 되고 이는 분류가 제대로 되지 않았을 확률이 높다는 것과 직관적으로 같다는 것을 확인할 수 있다.

[역전파]

이제까지 딥러닝 모델의 시작인 퍼셉트론부터 MLP, 모델의 오차 계산까지 다뤄보았다. 사실 여기까지의 내용만 보면 딥러닝의 성능이 탁월하게 좋은 이유가 부족하다고 생각할지도 모른다.

하지만 딥러닝의 성능이 탁월히 좋은 이유는 바로 이제 다룰 딥러닝의 학습에 있다.

그리고 딥러닝 학습에서의 핵심이 바로 이번 단원의 역전파(Backpropagation)이다.

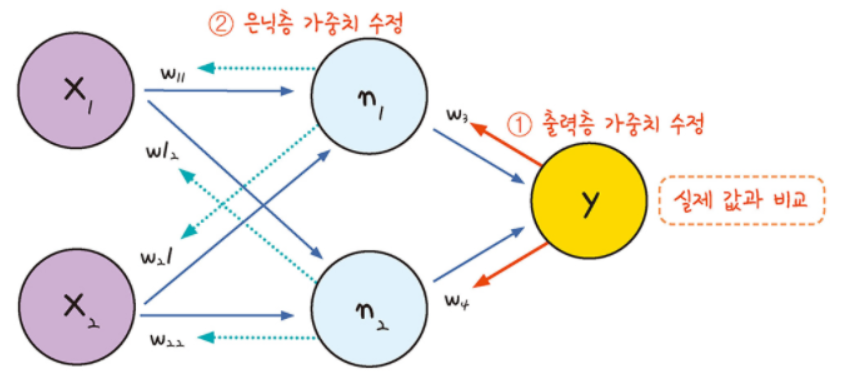
역전파란 실제 값과 모델의 예측 값 사이 얼마나 차이가 나는지 확인하고 그 오차를 바탕으로 가중치와 편향을 뒤에서부터 앞으로 갱신해가는 것을 의미한다.

그리고 역전파는 경사하강법을 통해 오차가 최소화되는 방향으로 최적화(Optimization)되고 미분의 연쇄법칙(Chain Rule)을 통해서 그 값이 계산된다.

[경사하강법]

가중치를 최적화하는 방법은 일반적으로 경사하강법 즉, Gradient Descent 기반의 최적화 기법이 사용된다.

따라서 경사하강법 알고리즘에 대해 먼저 살펴보자.

경사하강법은 함수의 기울기(Gradient)를 이용하여 독립변수 값들을 어디로 옮겼을 때 함수가 최소가 되는지를 알아보는 방법이다. 기울기가 양수라는 것은 독립변수 $x$ 값이 커질수록 함수 값이 커진다는 것을 의미하고, 반대로 기울기가 음수라면 $x$값이 커질수록 함수의 값이 작아진다는 것을 의미한다.

또한 기울기의 값이 크다는 것은 단위당 변화가 큰 지점이라는 것을 의미하기도 하지만 또 한쳔으로는 $x$의 위치가 최소값 혹은 최댓값에 해당되는 $x$ 좌표로부터 멀리 떨어져있는 것을 의미하기도 한다.

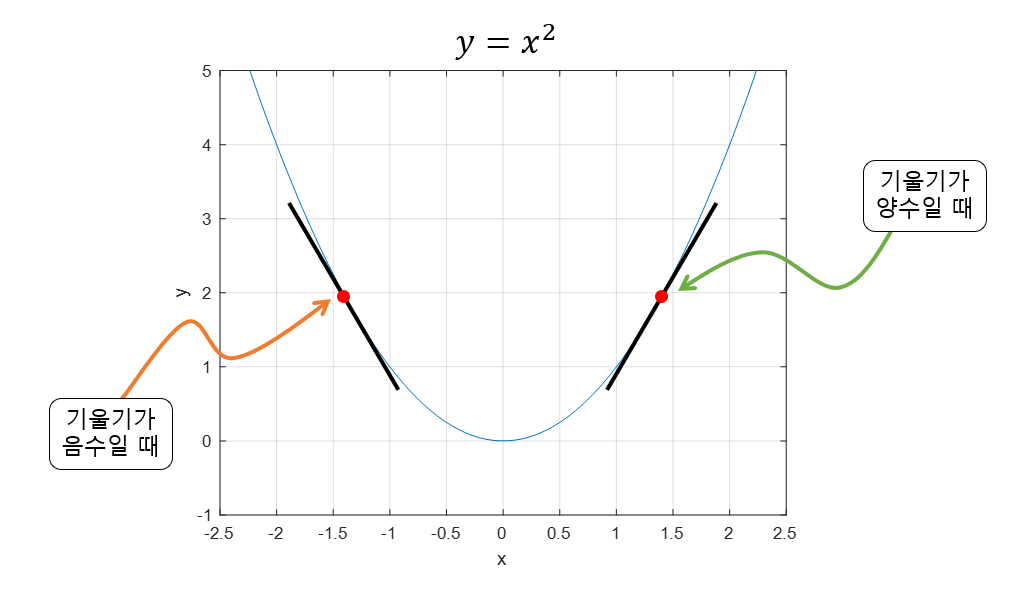
우리는 경사하강법을 통해 함수의 최소값을 구해야 하므로 특정 값 $x$에서 기울기가 양수이라면 음의 방향으로 $x$를 옮겨야 하고 반대로 기울기가 음수라면 양의 방향으로 $x$로 옮겨야 함을 파악할 수 있다.

이를 다음과 같이 수식으로 나타낼 수 있다.

여기서 $x_i$와 $x_{i+1}$은 각각 $i$번째, $i+1$번쩨 계산된 $x$의 좌표를 의미한다.

즉 기울기의 부호를 통해 가중치를 최소화하는 방향을 파악할 수 있다.

그럼 이동 거리는 어떻게 계산할 수 있을까?

미분 계수(기울기)값은 극소값에 가까울 수록 그 값이 작아진다.
(극대값에 가까울 때에도 미분 계수는 작아지지만 극대값에 머물러 있는 경우는 극히 드물기 때문에 이 문제에 대해서는 고려하지 않음)

따라서, 이동거리에 사용할 값을 gradient의 크기와 비례하여 이동 거리를 설정하면 현재 $x$의 값이 극소값에서 멀 때는 많이 이동하고, 극소값에 가까워졌을 때는 조금씩 이동할 수 있게 된다.

즉, gradient 값을 직접 이용하되, 이동 거리를 적절히 사용자가 조절 할 수 있게 수식을 조정해 줌으로써 상황에 맞게 이동거리를 맞춰나갈 수 있게 하면 된다.

이때, 이동 거리의 조정 값을 보통 step size라고 부르고 기호는 $\alpha$로 사용한다.

따라서 최종 수식은 다음과 같이 계산할 수 있다.

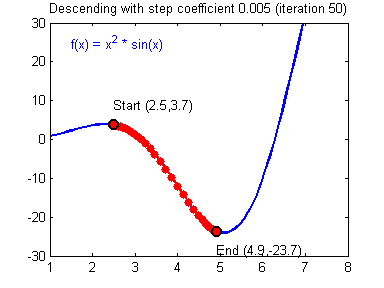
그리고 이를 다변수 함수로 확장하면 다음과 같은 식으로 나타난다.

($\nabla$가 뭔지 궁금하다면: 미분함수와 편미분 함수 단원 참고)

그리고 이를 가중치 업데이트 식으로 변환하면 아래와 같다.

• 학습률(learning rate): $\alpha \to$ hyper-parameter

경사하강법 참고 링크!

[미분의 연쇄법칙]

그럼 이번엔 미분의 연쇄법칙, Chain Rule을 알아보자.

연쇄법칙(Chain Rule)이란 "합성함수의 미분은 합성함수를 구성하는 각 함수의 미분의 곱으로 나타내어진다." 라는 의미다.

식으로 나타내면 다음과 같이 나타낼 수 있다.

위 식을 통해 가중치 $w_i$ 변화에 따른 Cost function $L$의 변화량을 계산할 수 있다.

[역전파 계산]

그럼 이제 경사하강법과 미분의 연쇄법칙을 적용하여 역전파를 계산하는 문제를 한번 해결해보자.

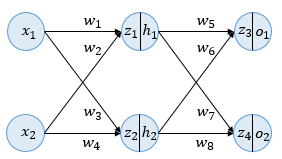
다음과 같이 입력층, 은닉층, 출력층 총 3개의 층으로 구성된 딥러닝 모델이 있다고 하자. 이때 은닉층과 출력층의 활성화 함수는 앞에서 다룬 Sigmoid function을 사용하며 인공 신경망에 존재하는 모든 가중치 $w$에 대해 역전파를 통해 업데이트 하며 편향 $b$는 고려하지 않는다.

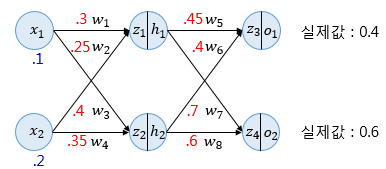
위와 같이 값들이 주어졌을 때 역전파를 진행하기 전 순전파 과정부터 계산해보자.

각 입력은 입력층에서 은닉층 방향으로 향하면서 각 입력에 해당하는 가중치와 곱해지고, 결과적으로 가중합으로 계산되어 은닉층 뉴런의 시그모이드 함수의 입력값이 된다. 아래에서 $z_1$과 $z_2$는 시그모이드 함수의 입력으로 사용되는 각각의 값이다.

$z_1$, $z_2$가 각각의 은닉층 노드에서 시그모이드 함수를 거친 최종 출력값은 $h_1$, $h_2$가 되며 아래의 결과와 같다.

또다시 $h_1$, $h_2$는 출력층의 노드로 가며, 이때 다시 각각의 값에 해당하는 가중치와 곱해진 후 가중합 되어 출력층 뉴런의 시그모이드 함수의 입력값이 된다. 식에서는 각각 $z_3$과 $z_4$에 해당한다.

$z_3$, $z_4$는 출력층의 뉴런에서 시그모이드 함수를 지나 $o_1$, $o_2$가 되고 이 값들이 이 인공 신경망에서 최종적으로 계산한 출력값 즉, 예측값이 된다. 수식으로 계산한 결과는 아래와 같다.

이제 예측값과 실제값 사이의 오차를 계산하여야 한다.

여기서 오차를 계산하기 위한 손실함수로는 평균제곱오차(MSE)를 사용하였으며 식에서 실제 값을 $target$으로, 예측 값을 $output$로 표현했다. 그리고 각 오차를 모두 더한 전체 오차가 $E_{total}$이 된다.

순전파가 입력층에서 출력층으로 향한다면 역전파는 반대로 출력층에서 입력층 방향으로 계산하면서 가중치를 업데이트한다. 출력층 바로 이전의 은닉층을 N층이라고 하였을 때, 출력층과 N층 사이의 가중치를 업데이트하는 단계를 역전파 1단계, 그리고 N층과 N층의 이전층 사이의 가중치를 업데이트 하는 단계를 역전파 2단계라고 해보자.

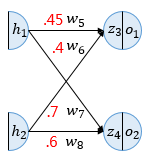
역전파 1단계에서 업데이트해야할 가중치는 $w_5, w_6, w_7, w_8$ 총 4개이다. 원리 자체는 동일하게 적용되므로 $w_5$를 예시로 업데이트를 진행해보자.

경사하강법을 수행하여 가중치 $w_5$를 업데이트하기 위해선 $\frac{\partial E_{total}}{\partial w_5}$를 계산해야한다.

이를 위해 미분의 연쇄법칙에 따라 아래와 같이 풀어서 계산할 수 있다.

위의 식에서 우변 각 항에 대해 첫번째 항부터 계산해보면 $E_{total}$이므로 아래와 같다.

이에 $\frac{\partial E_{total}}{\partial o_1}$은 다음과 같다.

이제 두번째 항을 살펴보자.

$o_1$이라는 값은 시그모이드 함수의 출력값이며, 시그모이드 함수의 미분은 아래 식에 따라 $f(x) \times (1-f(x))$이다.

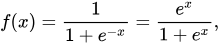
따라서 두번째 항의 미분 결과는 다음과 같다.

마지막으로 세번째 항은 $h_1$과 동일하므로 다음과 같다.

그럼 이제 우변의 모든 항을 곱하면 다음과 같은 결과가 도출된다.

이제 앞서 배웠던 경사하강법의 가중치를 업데이트할 수 있다. 하이퍼파라미터에 해당하는 학습률 $\alpha$를 0.5라고 가정하면 다음과 같은 식이 계산된다.

이와 같은 원리로 $w_6^+, w_7^+, w_8^+$을 계산할 수 있다.

그럼 이제 역전파 2단계로 넘어가보자.

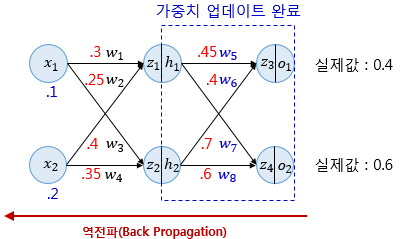
이때 유의할 점은 현재 인공 신경망은 은닉층이 1개밖에 없으므로 이번 단계가 마지막 단계이지만 은닉층이 더 많은 경우라면 입력층 방향으로 한 단계씩 계속해서 계산해가야 한다.

그럼 이제 가중치 $w_1, w_2, w_3, w_4$를 업데이트 해보자. $w_1$도 미분의 연쇄법칙에 따라 아래와 같이 풀어서 사용할 수 있다.

위 식에서 우변의 첫번째 항인 $\frac{\partial E_{total}}{\partial h_1}$은 다음과 같이 다시 풀어서 쓸 수 있다.

따라서 첫번째 항을 분해 및 계산하면 아래와 같이 나타낼 수 있다.

이와 같은 원리로 $\frac{\partial E_{o_2}}{\partial h_1}$도 구합니다.

$\frac{\partial E_{total}}{\partial w_1}$을 구하기 위한 첫 항의 계산을 했으니, 이제 다른 두 항도 구하면 다음과 같다.

즉, $\frac{\partial E_{total}}{\partial w_1}$은 다음과 같다.

이제 앞서 배웠던 경사하강법을 이용해 가중치를 업데이트할 수 있다.

이와 같은 원리로 $w_2^+, w_3^+, w_4^+$을 계산할 수 있다.

이렇게 가중치를 업데이트 했으니 다시한번 순전파시켜 오차가 줄어들었는지 확인해보겠습니다.

기존 전체 오차 $E_{total}$가 $0.02397190$였으므로 1번의 역전파로 오차가 감소한 것을 확인할 수 있다.

이처럼 인공신경망의 학습은 오차를 최소화하는 가중치를 찾는 목적으로 순전파와 역전파를 반복하는 것을 의미한다.

[최적화 함수]

위 과정에서는 최적화 함수 즉, Optimizer로 경사하강법(아래 그림에서 GD)을 사용했지만 다음과 같이 다양한 Optimizer가 존재한다.

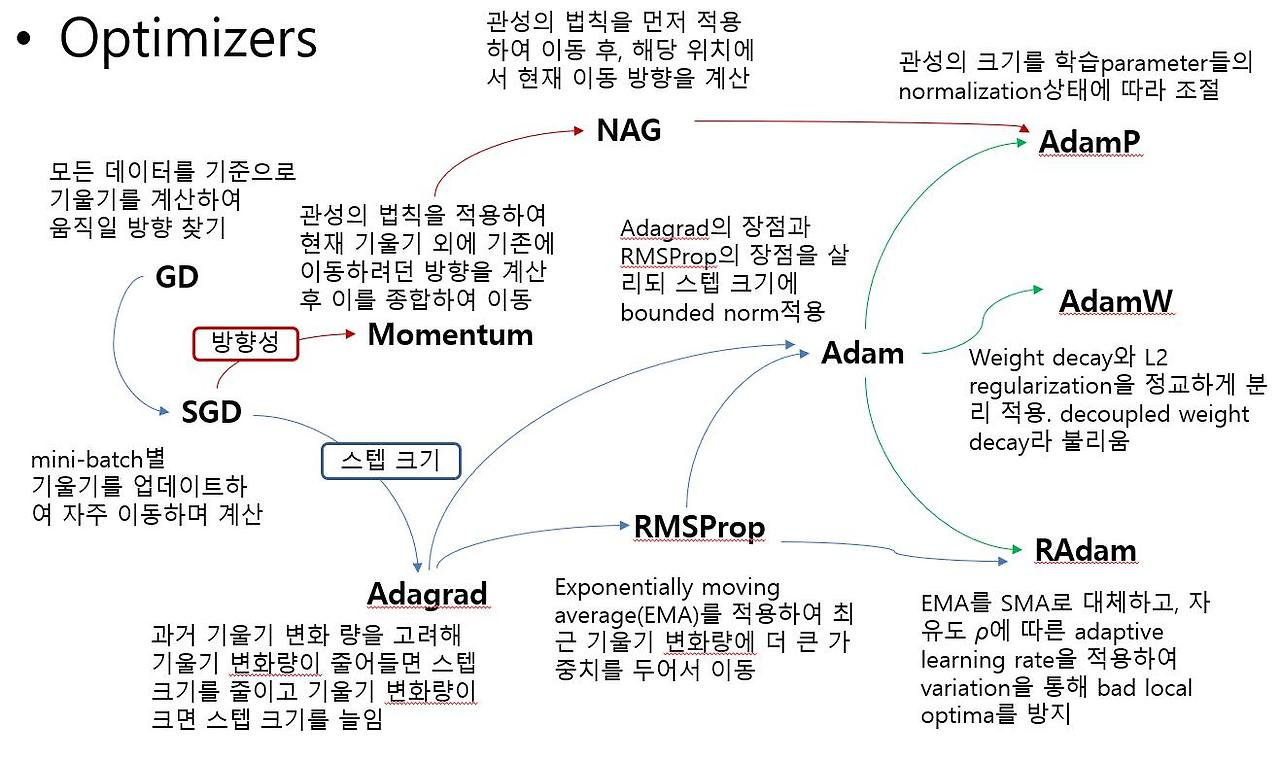
경사하강법을 기반으로 하여 방향성과 스텝 크기 두 관점을 바탕으로 Optimizer가 발전했으며 현재 주로 Adam이 자주 Optimizer로써 사용된다.

[Plus]

여기까지 기본적인 딥러닝의 내용을 개괄적으로 훑어보았다. 하지만 언급된 내용 외에도 규제화와 같이 일부 포함되지 않은 내용도 있으며, 간단하게 언급만 한 부분도 존재한다. 따라서 Deep Learning 시리즈에서는 MIT의 Deep learning이라는 책을 참고하여 이를 공부하며 추후 자세하게 다루고자 한다.