이번 논문은 CTGAN이라는 데이터 증강에 사용되는 모델을 통해 어떤 비율로 합성데이터를 만들어야하는지에 대한 논문입니다.

[데이터 불균형성의 문제]

이진분류와 같은 분류문제에서는 종속변수의 Class끼리 수가 너무나도 다를 수 있다.

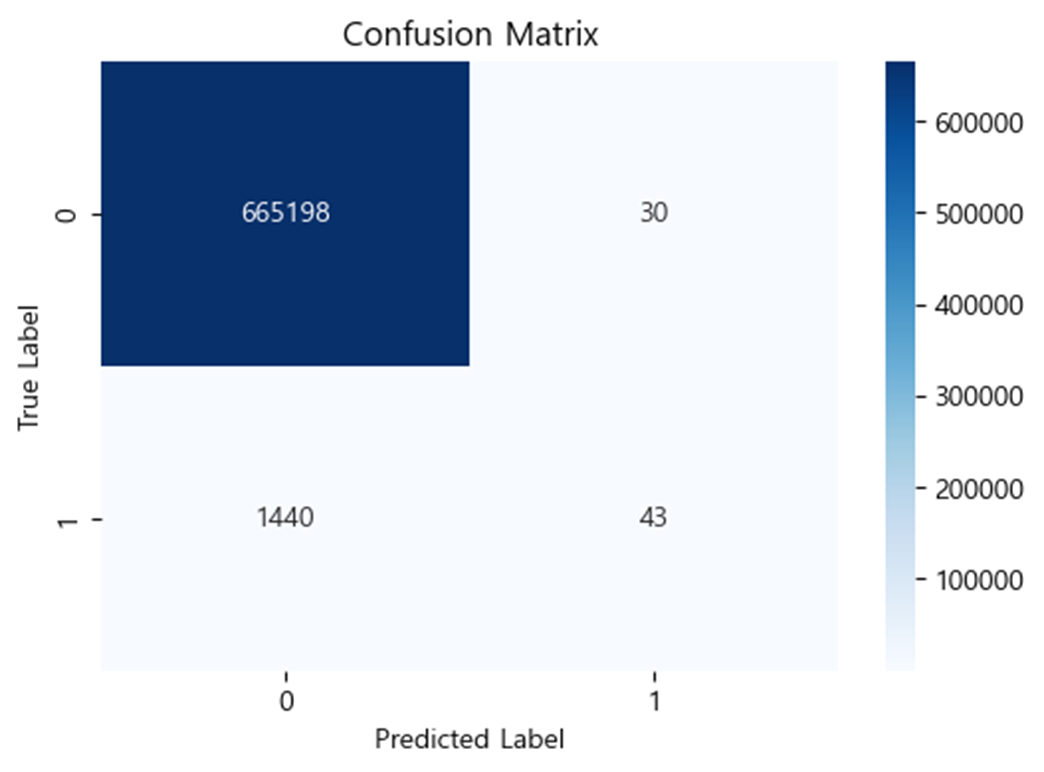
예를 들어 반도체 공정 불량품을 맞추는 AI가 있다면, 정상/불량이라는 종속변수의 두가지 Class 중에 정상에 해당하는 데이터는 많은 반면 불량에 해당하는 데이터는 1% 정도일 수도 있다.

이때 모델은 이러한 데이터의 불균형성이 존재할 경우 적은 수의 Class 분포를 제대로 학습하지 못해 과대적합이 발생할 수 있다.

따라서 SMOTE나 최근엔 CTGAN과 같은 데이터 증강기법을 통해 데이터의 불균형성을 해소하여 이 문제를 해결할 수 있다.

[GAN]

테이블 데이터를 증강하는 모델은 크게 베이지안 네트워크(Bayesian Network)를 활용한 방법(CLBN, PrivBN 등)과 딥러닝 모델인 생성적 적대 생성망(GAN)을 활용한 방법 (MedGAN, VeeGAN, TableGAN, CTGAN 등)이 있다.

그러나 베이지안 네트워크기반 방법은 고차원 데이터와 같은 복잡하고 비선형적인 데이터 패턴을 모델링하기 어렵다는 한계가 있어, 최근에는 GAN을 활용한 딥러닝 기반의 데이터 증강 모델 연구가 활성화되고 있다.

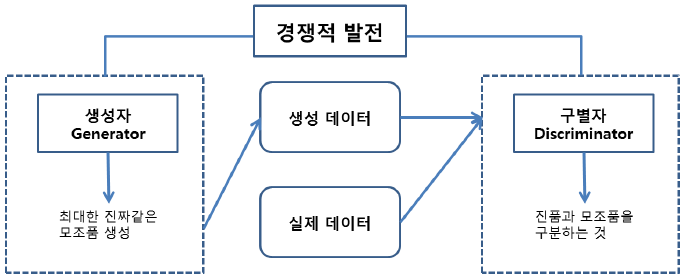
GAN은 생성자(Generator)와 판별자(Discriminator)의 구조를 가져 다양한 유형의 데이터를 생성할 수 있다. 생성자는 랜덤한 노이즈나 입력 데이터를 받아 실제 데이터와 유사한 데이터를 생성한다.

이렇게 생성된 데이터는 처음에는 랜덤하고 무질서하지만 훈련 과정을 통해 실제 데이터와 더욱 유사한 패턴을 학습하게 된다.

판별자는 생성자에서 만들어진 데이터와 실제 데이터를 구분하려고 노력하며 입력된 데이터가 실제인지 생성된 데이터인지 판별하는 역할을 한다.

생성자는 더욱 실제와 유사한 데이터를 생성하려고 노력하고, 판별자는 생성자가 만든 합성 데이터와 실제 데이터를 구분하려고 노력한다. 이 경쟁 과정에서 생성자는 점차적으로 더 나은 데이터를 생성하게 된다.

즉, GAN의 핵심 아이디어는 생성자와 판별자가 서로 경쟁하며 학습하는 것이다.

그래서 GAN, Generative Adversarial Network에 Adversarial가 이러한 모델에 정의에 포함된 이유이기도 하다.

특히, 이런 Tabular data(테이블 데이터)에 뛰어난 성능을 가진 딥러닝 모델이 CTGAN이다.

[CTGAN]

조건부 적대적 테이블 생성망(Conditional Tabular GAN, CTGAN)은 GAN을 기반으로 하는 딥러닝 모델로, 연속과 불연속 데이터가 혼재되어있는 테이블 데이터에서 데이터를 생성하는 테이블 데이터 증강 모델이다.

일반적인 적대적 생성망은 다수의 클래스 데이터 위주로 학습되기 때문에 그 희소한 값을 잘 학습하지 못해, 데이터 재현 시 다수의 클래스만 재현하는 문제가 발생하게 된다.

그러나 조건부 적대적 생성망은 이러한 문제에 대응할 수 있다. 조건부 적대적 생성망을 통해 희소한 클래스를 생성하도록 범주형 열을 조건으로 넣어주어, 생성자가 학습 과정에서도 조건으로 희소한 범주형 속성값에 노출되도록 조절 가능하기 때문이다.

데이터 증강 모델을 사용하여 합성 데이터를 만들어 데이터를 증강하는 것과 희소 데이터를 단순히대량으로 복제하여 수를 늘리는 것(오버샘플링)은 차이가 있다. 오버샘플링은 기존 데이터의 특성만 반영하여 과적합 모델로 이어질 수 있다는 한계가 있다.

CTGAN 데이터 증강 모델은 이웃 정의(Defining Neighborhoods)를 통해 희소한 데이터 사이의 일반적인 공통점을 식별하여 실제자료와 유사한 분포를 가진 맥락있는 합성 데이터를 생성할 수 있다는 장점이 있다.

[실험]

실험은 테이블 데이터의 증강 시나리오에 따라 구분하였다. 먼저 시나리오 1인 원본 데이터의 사이즈가 작은 경우에는, 합성 데이터를 원본 데이터의 0.5배, 1배, 2배, 3배, 5배로 각각 증강하여, 원본 데이터와 합성 데이터의 5가지의 비율(1:0.5, 1:1, 1:2, 1:3, 1:5)을 구성하였다.

다음으로 원본 데이터에서 이상 데이터(소수 Class)만 증강하는 시나리오 2에서는, 정상 데이터와 이상 데이터의 비율을 기존의 1:0.001에서 다음과 같도록(1:0.005, 1:0.01, 1:0.05, 1:0.1) 이상 데이터를 각각 5배, 10배, 50배, 100배 증강하였다.

학습된 모델을 실제 데이터와 합성 데이터의 각 테스트 데이터에 적용하여 각각의 F1_Real과 F1_Fake 점수, 그리고 자카드 유사도를 구하여 적절한 증강 비율을 확인하였다.

[실험 결과]

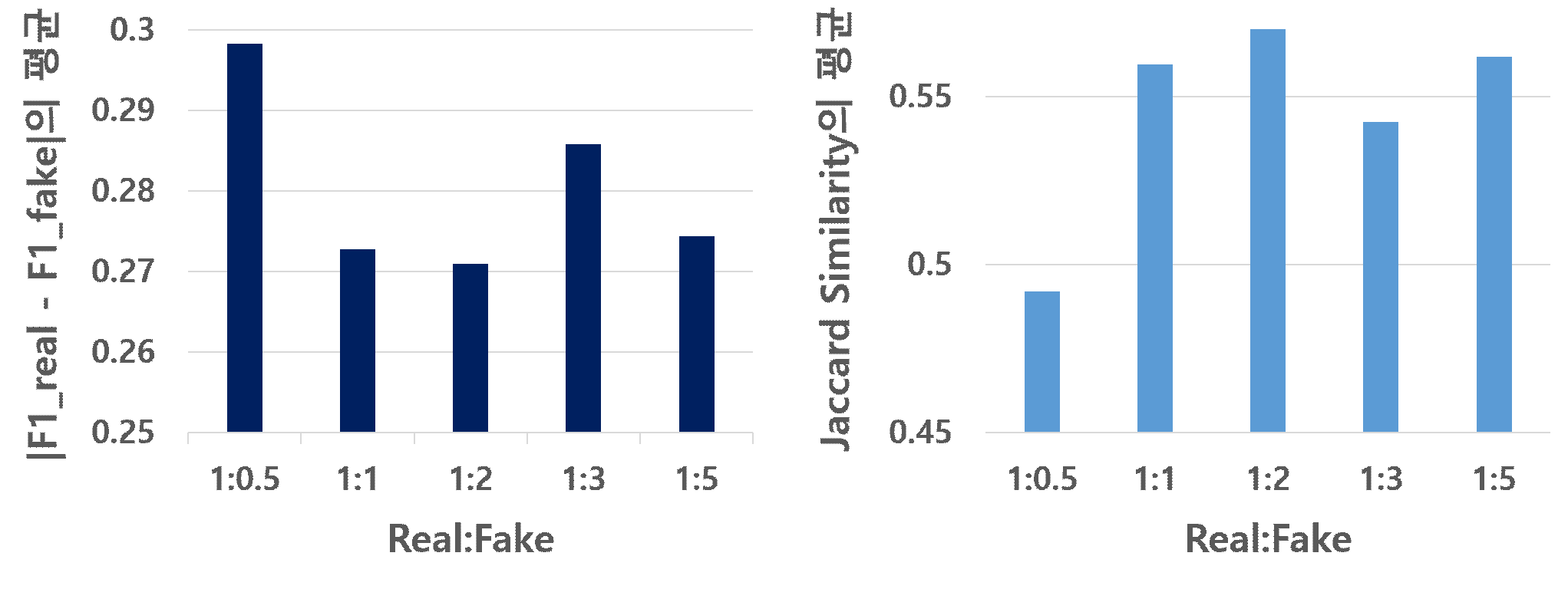
시나리오 1에서 전체 데이터를 늘리는 경우, 실제 데이터와 합성 데이터의 비율별로 |F1_Real-F1_Fake|의 점수와 자카드 유사도의 평균 점수를 비교하면 (그림 2)와 같다.

증강 비율별 |F1_Real-F1_Fake|의 평균 점수를 보면, 합성 데이터를 원본 데이터의 2배로 증가시켰을 때 그 차이가 가장 작아 합성 데이터와 원본 데
이터의 유사도가 가장 높고, 0.5배로 증가시켰을 때는 가장 낮은 유사도를 보였다. 자카드 유사도의 평균 점수의 경우에도 마찬가지로 합성 데이터를 원본 데이터의 2배로 늘렸을 때 유사도가 가장 높게 나왔으며, 0.5배로 늘렸을 때 가장 낮게 도출되었다.

그러나 |F1_Real-F1_Fake|의 경우 최고와 최저 성능의 차이가 0.03 미만이며, 자카드 유사도의 경우 0.01 미만으로 그 차이가 근소하여 본 실험의 시나리오 1에서는 합성 데이터를 실제 데이터의 5배까지 증강한다 하더라도 데이터의 특성에 큰 변화를 발생시키지 않는 것을 확인할 수 있다.

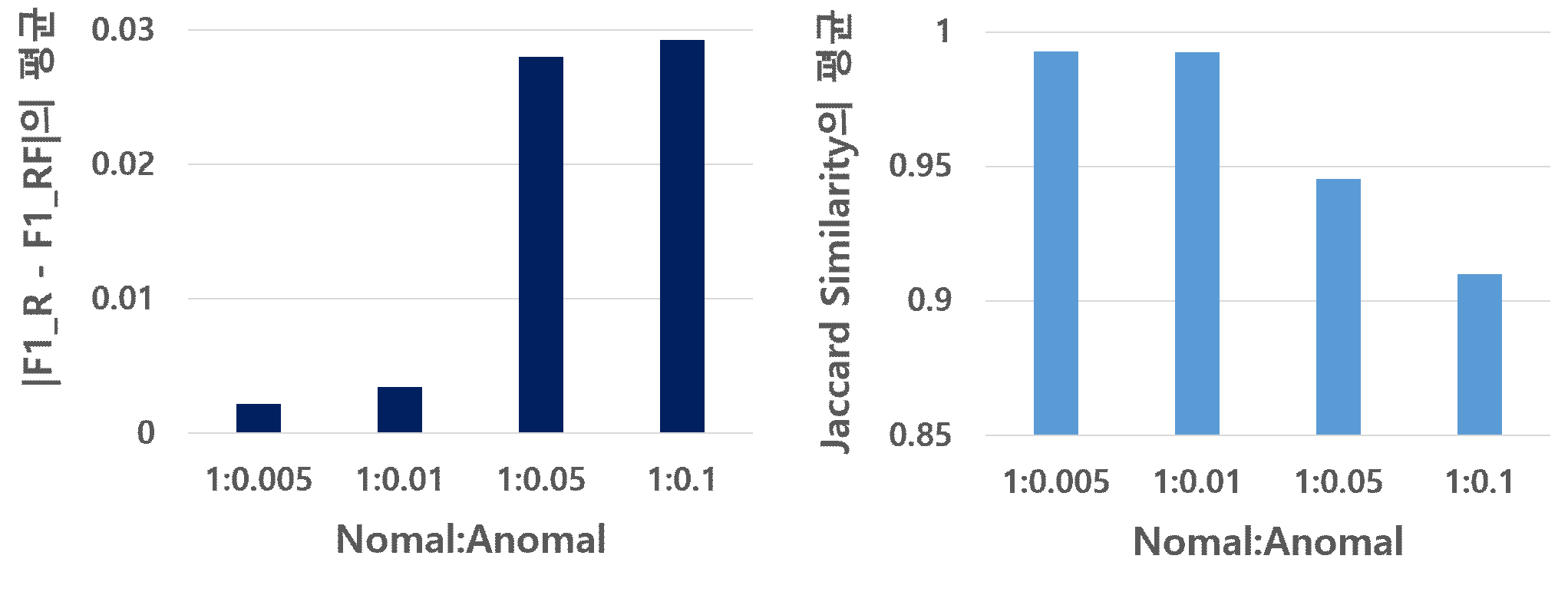
시나리오 2의 경우, 원본 이상 데이터가 충분하지 않아 두 데이터 간 유사성을 평가하기 어려웠다. 따라서 실험에서 설정한 정상 데이터와 이상 데이터의 비율 별로 합성한 각 이상 데이터 F를 전체 데이터 R에 더하여 RF 데이터를 만들었으며, R과 RF의 유사성을 비교하였다.

|F1_R–F1_RF|의 평균 점수를 보면 이상 데이터를 기존의 5배로 합성하여 전체 데이터와의 변화가 가장 적은 1:0.005의 경우가 가장 유사도가 높고, 이상 데이터를 100배 늘린 1:0.01의 경우가 유사도가 가장 낮게 나왔으나 그 차이는 근소하다.

자카드 유사도의 경우에도 비슷한 결과가 도출되었다. 그리고 |F1_R–F1_RF|의 평균과 자카드 유사도의 평균 점수 모두 전반적으로 이상 데이터의 합성 배율을 최대 100배 가까이 증강시킨다 하더라도 데이터의 특성 변화에 유의미한 영향을 미치지 않는것을 확인하였다.