이번 글은 ICLR 2023에서 accept된 시계열 예측 모형 KNF(Koopman Neural Forecasting)에 대해서 알아보도록 하겠습니다.

본 논문에서 제안하는 시계열 모델은 비정상성을 가진 시계열 데이터의 예측을 주목적으로 하는 모델입니다.

항상 시계열 공부를 하면서 정상성을 만족해야만 하는 모델들이 너무 많았고, ARIMA와 같은 기존 통계적 모델이 예측 성능 면에서 월등한 것도 아니기 때문에 정상성 가정을 넘어서는 최신 시계열 모델에 대해 공부하고 싶었는데 마침 잘 소개된 영상이 있어서 가지고 왔습니다.

또한 시계열 예측을 필요로 하는 데이터의 경우 항상 들었던 생각이 "시계열 데이터의 경우 모델을 검증할 때 Train/Test로 분리하는 과정에서 상반기/하반기로 분리하게 되면 Distribution Shift, 즉 시간에 따라 데이터의 분포가 달라지는 걸 고려해야 올바른 분석이지 않을까"하는 생각이었는데 마침 이 연구에서 그에 대한 답을 얻을 수 있을 것 같아서 더 맘에 드는 연구인 것 같습니다.

따라서 제안 모델에 대해 다루는 부분이 어렵다면 (1)편에서 시계열 데이터 특성을 다루는 부분이라도 읽어보시면 시계열 분석에 도움이 될 듯 합니다!

자료는 서울대학교 산업공학과 DSBA 연구실 소속 박진우 님의 유튜브 영상을 참고하였으며 링크는 아래와 같습니다.
DSBA KNF 논문 리뷰 영상

또한 본 논문은 구글 클라우드 AI 분들이 직접 연구하신 논문이여서 더 좋은 것 같고, SOTA에서도 Star가 엄청난 논문입니다. 논문과 깃허브 링크는 아래 링크를 통해서 확인할 수 있습니다.
KNF 논문 & 깃허브

(1)편에서 시계열 데이터의 특성과 모델 setting, 모델 아키텍처 중 Leveraging Predefined Measurement functions을 살펴 보았습니다.

따라서 이번 (2)편에서는 모델 아키텍처 설명 중 Global and Local Koopman Operators에서부터 이어서 설명드리겠습니다.

[Method]

[Model architecture]

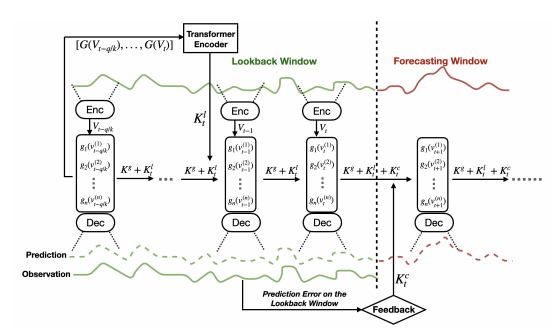
Global and Local Koopman Operators

전통적인 Koopman thoery는 무한 차원을 유한 차원으로 근사하자는 게 기본 Concept이므로 전통적인 Koopman thoery을 따르면 measurement vector $G(V_t)$는 infinite dimension을 가지므로 학습이 불가능합니다.

하지만 제안 연구에서는 Encoder에서 finite한 approximate를 학습을 하고 있기 때문에 $G(V_t)$ 역시 finite Koopman-invariant subspace를 형성한다고 가정하여 이론적인 문제를 해결합니다.

다음으로 이상적으로 찾아야 하는 Koopman operator은 시간이 지나에 따라 measurements를 시간적으로 가장 잘 forwading 시키는 finite matrix를 의미합니다.

즉 아래 식에서 $g(x_t)$를 g(x_{t+1})로 잘 forward시키는 Koopman operator $K$를 찾는 것

이때 Koopman matrix는 time-step과 feature에 따라 달라져야 하지만 시계열의 전역적인 행동 또한 포착할 수 있어야 합니다.

따라서 전체적인 경향성과 dynamics를 모두 모델링 하기 위해 Global operator $K^g$와 Local operator $K^l_t$를 따로 나눠서 사용합니다.

• Global operator $K^g$는 nd $\times$ nd의 학습이 가능한 matrix로 전체 시계열에서 공유함으로써 Trend와 같이 전체적으로 공유되는 동작 학습이 목적

• Local operator $K^l_t$는 Lookback window 내 샘플에 특화된 local dynamics 포착이 목적
  $\to$ Lookback window 내에서 Autoregressive하게 지속적으로 학습하여 window 내의 distribution shift에 적용하게 하는 것이 목표

Global operator와 Local operator를 어떻게 도출할건지에 대해선 제안 연구에서는 Single-head Transformer encoder에서 attention matrix(1)를 바탕으로 Local operator를 계산하며 Global operator은 Linear layer를 통하여 도출합니다.

Feedback Loop

Lookback window 중간에 갑작스런 Distribution shift가 발생한다고 가정하면 데이터 기반 모델 특성 상 발생한 변화의 이전과 이후 두 가지 distribution에 fitting 하고자 할 것이나 기존 연구에서는 단일 행렬만을 사용하기에 여러 분포를 모델링하기 충분하지 않았습니다.

이에 해당 연구에선 Lookback window 내부에서 발생한 Prediction error를 기준으로 하여 adjustment operator $K^c_t$를 사용하여 추가적인 feedback loop를 진행하여 이를 해결하고자 했습니다.

adjustment operator $K^c_t$은 Lookback window 내에서 Prediction을 지속적으로 도출하여 얻어진 예측값과 실제값 차이를 MLP에 입력 데이터로 넣음으로써 구해집니다.

따라서 최종 예측 시에는 세 가지 Operator의 합을 사용합니다.

즉, feedback loop는 lookback window 내부에서의 distribution shift가 발생할 경우 이를 감지하고, Global 및 local operator를 lookback window 내의 마지막 분포에 맞추기 위하여 설계된 것이라고 할 수 있습니다.

Loss function

해당 연구의 모델은 3가지 Loss를 바탕으로 학습이 진행됩니다.

1) $L_{rec} = l(X_t, \phi(G(\psi(X_t)X_t))), \quad t \geq0$
Reconstruction loss로 Decoder $\phi$가 measurements로부터 시계열 데이터를 올바르게 구성하기 위함

2) $L_{back} = l(X_{t-q/k+i}, \phi((K^g+K^l_t)^iG(\psi(X_{t-q/k})X_{t-q/k}))), \quad 0 \lt i \le q/k$
Lookback window에서의 Prediction loss로, global/local operator의 합이 lookback window에서 가장 적합한 propagation matrix가 되도록 하기 위함

3) $L_{forw} = l(X_{t+i}, \phi((K^g+K^l_t+K^c_t)^iG(V_t))), \quad i \gt 0$

Prediction window에서의 Prediction accuracy를 위한 loss term으로, Feedback loop가 Koopman operator에 올바른 adjustment를 학습하게 하기 위함.

[Experiment]

해당 단원은 성능을 검증하는 파트로 중요한 부분만 가지고 왔습니다.

Data 설명 지표

1) Forecastability: 시계열의 푸리에 분해의 엔트로피를 이용하여 계산되며 계산된 값을 1에서 빼준 값으로 정의

2) Lyapunov exponent: dynamical system이 초기 조건에 얼마나 민감한지를 측정하는 지표

3) Trend: 시계열에 선형 회귀를 fitting 시킨 후 기울기를 해당 시계열의 크기로 scaling 시킨 지표

4) seasonality: ACF test 사용

Interpretability Results

KNF는 Koopman operator의 spectral analysis를 제공한다는 것이 또 다른 장점!
$\to$ 이를 통해 설명력을 확보 가능함

학습된 KNF 내의 $K^g+K^l_t$에 eigen-decomposition을 통하여 개별 eigen-function이 무엇을 학습했는지 확인할 수 있으며 각 eigen-function은 서로 다른 역할(어떤 경우는 trend, 어떤 경우는 seasonality에 강점)을 함. 따라서 종합적으로 학습에 유의미하게 작용함을 확인 가능하다.

[Conclusion]

KNF는 분포 변화가 심한 시계열 데이터셋에서 가장 좋은 예측 성능을 보이며 해석 가능한 결과를 제공하기 때문에 큰 장점을 보임

• Perdefined measurement function을 활용하여 Neural network가 학습하기 어려운 비선형적이고 비정상성을 가지는 특성을 포착

• Global operator를 통해 전체 시계열에서 공통되는 특성을 학습하고 Local operator를 통하여 변화하는 temporal dynamics를 포착

• 학습된 operator를 시간에 따라 지속적으로 업데이트하기 위하여 feedback loop 사용

(1) : 추후 다룰 예정