이번 글은 ICLR 2023에서 accept된 시계열 예측 모형 KNF(Koopman Neural Forecasting)에 대해서 알아보도록 하겠습니다.

본 논문에서 제안하는 시계열 모델은 비정상성을 가진 시계열 데이터의 예측을 주목적으로 하는 모델입니다.

항상 시계열 공부를 하면서 정상성을 만족해야만 하는 모델들이 너무 많았고, ARIMA와 같은 기존 통계적 모델이 예측 성능 면에서 월등한 것도 아니기 때문에 정상성 가정을 넘어서는 최신 시계열 모델에 대해 공부하고 싶었는데 마침 잘 소개된 영상이 있어서 가지고 왔습니다.

또한 시계열 예측을 필요로 하는 데이터의 경우 항상 들었던 생각이 "시계열 데이터의 경우 모델을 검증할 때 Train/Test로 분리하는 과정에서 상반기/하반기로 분리하게 되면 Distribution Shift, 즉 시간에 따라 데이터의 분포가 달라지는 걸 고려해야 올바른 분석이지 않을까"하는 생각이었는데 마침 이 연구에서 그에 대한 답을 얻을 수 있을 것 같아서 더 맘에 드는 연구인 것 같습니다.

따라서 제안 모델에 대해 다루는 부분이 어렵다면 (1)편에서 시계열 데이터 특성을 다루는 부분이라도 읽어보시면 시계열 분석에 도움이 될 듯 합니다!

자료는 서울대학교 산업공학과 DSBA 연구실 소속 박진우 님의 유튜브 영상을 참고하였으며 링크는 아래와 같습니다.
DSBA KNF 논문 리뷰 영상

또한 본 논문은 구글 클라우드 AI 분들이 직접 연구하신 논문이여서 더 좋은 것 같고, SOTA에서도 Star가 엄청난 논문입니다. 논문과 깃허브 링크는 아래 링크를 통해서 확인할 수 있습니다.
KNF 논문 & 깃허브

[Overview]

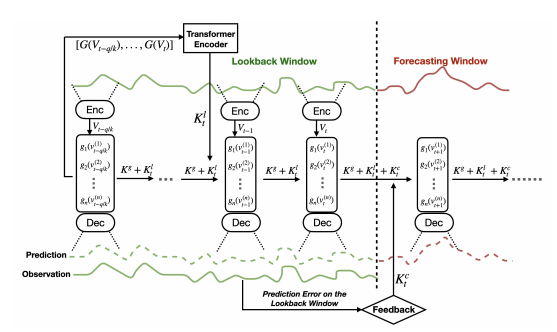
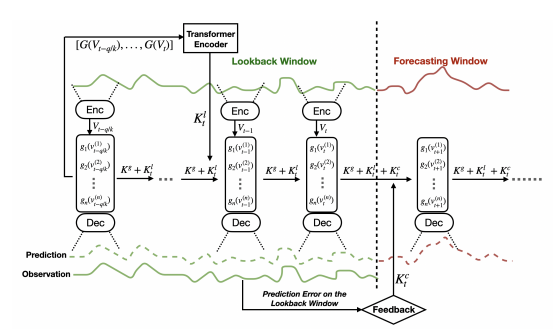
KNF(Koopman Neural Forecasting)은 한마디로 다음과 같습니다.
Non-Stationary timeseries를 분석하고자 동역학의 Koopman이론을 바탕으로 시계열 예측을 수행하는 모델!

Non-stationary 하다는 것은 Distribution Shift가 발생한다는 것입니다.

이때 우리는 머신러닝과 딥러닝에서 일반적으로 Test Data와 Train Data의 분포가 일치한다고 가정하고 모델을 사용하는데, Distribution Shift가 존재한다면 이 가정을 위배하는 상황이 생긴다는 의미입니다.

따라서 Distribution Shift 문제를 해결하는 건 어렵지만 중요한 문제라는 의미이고, 이에 본 논문에서는 Koopman 이론을 활용하여 이 문제를 해결하였습니다.

[Background]

[Timeseries data 특성]

정상성(Stationary)

시간의 흐름에 따라 평균이나 분산 등의 통계적인 특성이 변하지 않는 데이터로, 정상성이 보장되기 위해선 추세나 계절성이 존재하지 않아야 합니다.

정상성이 존재한다면 데이터의 시점이 어떻게 바뀌든 간에 데이터의 분포는 같습니다. 하지만! 현실의 데이터는 대부분 정상성을 가지지 못합니다.

이는 실제 데이터엔 Seasonality, Concept drift, Change point 등과 같이 변동성을 가지는 특성들이 많기 때문입니다.

• Concept Drift: 독립변수에서 부터 예측하려고 하는 "종속변수"의 의미/개념/통계적 특성(즉 데이터와 라벨의 관계성, 데이터의 해석 방법)이 모델 훈련때와 비교하여 변화가 있음을 의미함.

•  Data Drift: 모델의 훈련시 "독립변수"의 통계적 분포와 테스트 시/ 실제 배포 환경에서의 "독립변수"의 통계적 분포가 어떠한 변화에 의해 차이가 발생하고 있는 것을 의미한다. Feature drift나 Covariate shift라고 불림.

Distribution Shift

Distribution Shift는 시계열 데이터가 Non-Stationary 하면서 발생하는 기본적인 문제로, 시계열 데이터는 수집되는 특성 상 시간에 따라 특정 간격으로 순차적으로 수집되는데, 대체로 시간 변화에 따라 분표가 변화하며 이에 따라 발생하는 문제입니다.

이러한 분포의 차이는 Train Data와 Test Data 사이의 분포 차이가 발생하게 되므로 시계열 모델의 Generalization이 잘 되지 않는 결과를 초래하여 낮은 성능을 야기합니다. 따라서 시계열 데이터를 잘 다루기 위해서는 시간에 따른 분포 변화로 인한 통계적인 특성 변화를 잘 포착하는 것이 중요합니다.

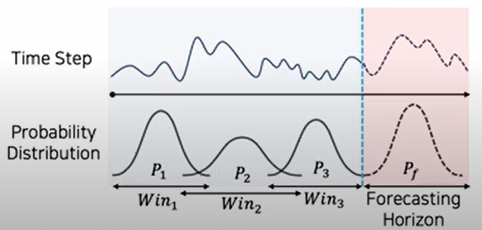
Distribution Shift의 원인

1. Train data, Test Data 사이에서 발생하는 Distribution Shift
2. 시간이 지남에 따라 분포 변화가 지속적으로 발생하는 경우
   $\to$ Concept Drift 및 Non-stationary process와 관련

대부분의 딥러닝 기반 접근 방식은 Stationary 시계열 데이터에서는 좋은 성능을 보이지만, 다양한 분포 변화를 보이는 데이터에 대해서는 약한 모습을 보입니다.

Keyword description

(1) Linear vs Nonlinear

모델의 출력결과와 입력값이 선형조합으로 표현될 수 있는지 없는지에 대한 차이입니다.

Linear 모형은 선형회귀, ARIMA 모델이 있으며 일반적으로 모델의 입력과 출력을 수식적으로 명확하게 보여줄 수 있어 설명력이 확보되는 모델이며, Non-linear 모형은 대표적으로 딥러닝 모형이 있고 이는 Black box 모델로 수식적으로 관계를 명확하게 설명할 수 없습니다. 대신 일반적으로 Linear 모형보다 예측력이 높다는 특징을 가지고 있습니다.

(2) Time-variant vs Time-invariant

Time-invariant란 시간이 지남에 따라서도 특성이 변하지 않는 시스템으로 입력 $X(t)$에 대한 출력이 $Y(t)$인 모델이 존재할 때 입력이 $r$만큼 늦어진 $X(t+r)$에 대해서도 동일하게 $r$만큼 늦어진 $Y(t+r)$의 출력이 도출됨을 보장할 수 있다는 의미입니다.

반면 Time-variant는 시간이 지남에 따라 특성이 변화하는 모델입니다.

Koopman theory

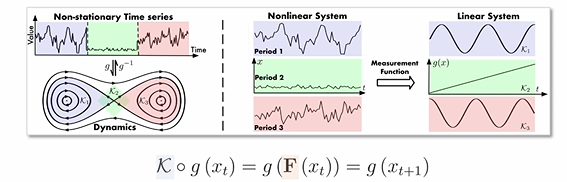
Koopman theory는 Nonlinear dynamic system 의 분석 및 예측을 특정한 Linear operator 를 바탕으로 수행하는 것이 목적입니다.

• Nonlinear dynamic system 은 특정 task에서 뛰어난 성능을 보일 수 있지만 매우 복잡한 구조를 가짐

• Linear operator은 비교적 간단하지만 다양한 수학적 도구와 기법으로 쉽게 분석할 수 있다는 장점 존재

• 즉, Koopman theory의 핵심 아이디어는 Nonlinear dynamic system을 묘사할 수 있는 Linear operator를 찾는 것!!

이를 바탕으로 Nonlinear dynamic system의 복잡성을 linear하게 변형하여 보다 직관적으로 이해하고 분석할 수 있습니다.

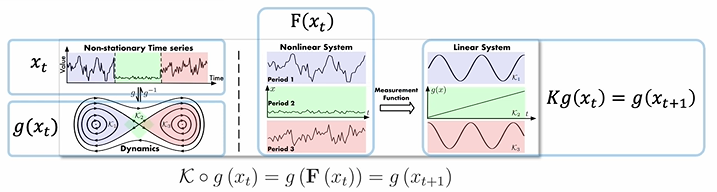
시계열 데이터는 위와 같이 해당 데이터가 가지는 내재적인 변동성(koopman 이론에선 Dynamic)을 바탕으로 이상적인 궤도(Trajectory)를 구성할 수 있는 function F로 표현할 수 있습니다.

이때 Discrete-Time dynamical system 가정에서는 이를 $x_{t+1} = F(x_t)$로 수식화가 가능합니다.

Non-stationary timeseries data $x_t$는 Time-variant dynamics를 가지기에, 이를 선형 연산이 가능하게끔 더 높은 차원의 공간으로 변환하고자 Measurement function $g$이용하여 비선형 함수를 더 높은 차원 공간에서 다룸으로써 선형 함수로 근사 하고자 합니다.

이때 Koopman operator K는 고차원 공간에서의 선형 연산자로, $g(x_t)$를 $g(x_{t+1})$로 선형 변환할 수 있으며 결국 찾고자 하는 것은 $Kg(x_t) = g(x_{t+1})$를 가능하게 하는 Koopman operator K이다.(우리는 $F(x_t)$를 찾을 수 없기 때문)

• "비선형 함수를 더 높은 차원 공간에서 다룸으로써 선형 함수로 근사" 예시

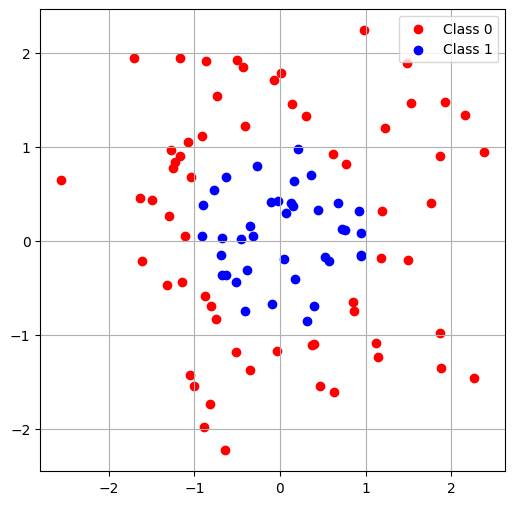
위와 같은 비선형 데이터를 고차원 공간에서 다루면 아래와 같이 선형 함수를 통해 나눌 수 있음.

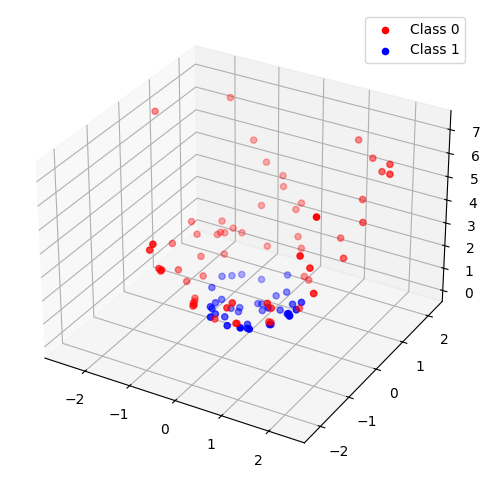
[Method]

[Contribution]

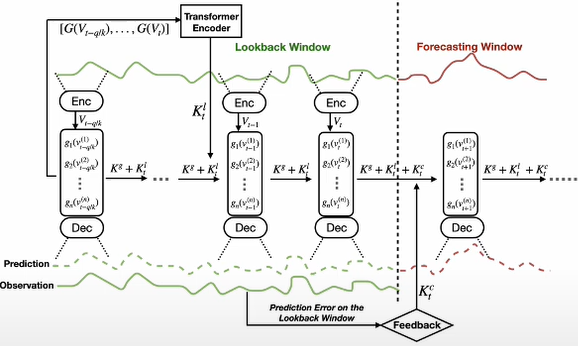
(1) Leveraging Predefined Measurement functions

• Predefined Measurement function을 Learned coefficients와 함께 사용하여 Timeseries를 functional space로 mapping

(2) Global and Local Koopman Operators

• Global Koopman Operators를 사용하여 공유되는 특성을 학습하고, Local Koopman Operators를 통하여 지역적인 변화 dynamics를 포착

(3) Feedback loop

• Forecasting error 에 기반하는 Feedback loop를 통합하여, 학습된 operator를 시간이 지남에 따라 재학습함으로써 long-term forecasting 성능을 유지

[Model setting]

우리는 과거의 값을 바탕으로 미래 값을 예측할 수 있는 functional map $f$를 찾는 것이 목적으로 다음과 같이 수식으로 나타낼 수 있습니다.

여기서, $q$는 얼마만큼의 데이터를 모델의 입력 데이터로 사용할 것인지에 대한 하이퍼파라미터인 Window length라 하며, $h$는 얼만큼 예측할 것인지에 대한 하이퍼파라미터인 forecasting horizon를 의미합니다.

Koopman theory는 어떠한 Nonlinear dynamic system이 가능한 모든 measurement function의 공간 안에서 작동하는 infinite-dimensional linear Koopman operator로 모델링될 수 있다는 것을 보여준다.

[Model architecture]

Leveraging Predefined Measurement functions

먼저, Koopman Space를 이루는 Measurement function의 Set 정의

어떠한 Measurement function을 사용해도 상관없지만 제안 연구에서는 Canonical nonlinear function 사용

Canonical nonlinear function이란

• polynomials, exponential functions, trigonometric functions 등이 존재
• Duffing oscillator, 유체역학 등의 분야에서 복잡한 dynamic system 모델링에 흔히 이용되며 DNN으로는 학습하기 어려운 high-nonlinear action을 표현 가능
• Canonical nonlinear function은 전통적으로 성능이 보장되는 case가 많았고, 이들은 모델에 학습 과정 중 일반화 성능을 얻기 위해 추가적으로 도입되는 편향인 inductive bias를 잘 반영하며 nonlinear 동작도 잘 포착할 수 있음

다음으로, 코딩 과정에서 데이터를 고차원의 데이터로 바꾸기 위해 Embedding을 하게 됩니다.

이때 만약 우리가 데이터를 8개의 dimension으로 Embedding하고 4개의 Predefined measurement function을 사용하게 된다면, 4개의 dimension에 대해서만 Predefined measurement function의 Coefficient로 구성이 되며 나머지 4개의 부분은 파라미터로써 추후 모델에서 역할을 하게 됩니다.

• Embedding: 일반적으로는 범주형인 값을 연속적인 숫자로 구성된 벡터로 변환하는 것으로, 특히 인공신경망에서는 임베딩은 원래 차원보다 저차원의 벡터로 만드는 것을 의미

• 원래 차원은 매우많은 범주형 변수들로 구성되어있으나 학습방식(인근에 모여있는 것들끼리 그룹화)을 통해 저차원으로 대응되며 인공신경망의 임베딩은 수천 수만개의 고차원 변수들을 몇백개의 저차원 변수로 만들어 주고, 또한 변형된 저차원 공간에서도 충분히 카테고리형 의미를 내재하기 때문에 차원축소 관점에서도 유용함

이는 뒤에서 다시 다루도록 하겠습니다.

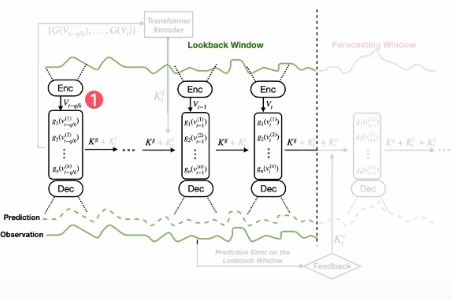
이제 모델에 입력 시계열 데이터가 들어온다면 모델이 어떻게 작동하는지 알아봅시다. 중요한 부분입니다!

어떠한 입력 시계열 데이터가 들어온다면 Encoder의 입력으로 사용하여 Measurement function의 계수 $\Psi(X_t)$로 사용합니다. $\Psi : \mathbb{R}^{d \times k} \to \mathbb{R}^{n \times d \times k}$

이 입력 시계열 데이터가 Encoder를 통해서 나온 결과를 그대로 이용하는 게 아니라 Measurement function의 계수를 향후 모델링 과정에서 사용하게 됩니다.

• $\Psi(X_t)$는 사전에 정의된 Canonical nonlinear function의 계수를 의미하며, 해당 계수들은 각 Measurement function이 어떻게 입력데이터의 특정 부분(변수, 시점)에 어떻게 적용될지 결정하게 된다.

이때 하나의 Window 내에서도 Distribution shift가 발생할 수 있기 때문에 하나의 Window 내에서도 다양한 구간으로 나누어 모델링을 진행합니다.

위 과정을 통해 Encoder의 output인 계수를 구하고나선, 원본 데이터의 값을 함께 고려함으로써 최종적인 계수 $V_t = [V_t^{(1)}, V_t^{(2)}, \dots, V_t^{(n)}] \in \mathbb{R}^{n \times d}$를 도출합니다.

이때 원본 데이터의 값을 함께 고려하는 과정을 아래와 같이 이뤄집니다.

• $V_t[i,j]$
  $\to$ encoder를 거친 후 Representation과 원본 시계열 데이터의 Linear transformation. 즉, 해당하는 시계열 데이터가 가지는 동역학적인 특성을 measurement function의 계수로 변환한 것

• $\psi(X_t)[i,j,l]$
  $\to$ encoder를 바탕으로 입력 시계열 데이터에서의 각 시간 스텝, 특성, 측정함수에 대응하는 가중치 값을 생성

• $X_t[j, l]$
  $\to$ $t$ 시점에서의 입력 시계열 데이터

이어 다음 과정을 살펴봅시다.

앞에서 구한 $V_t$를 활용하여 Predefined measurement function을 적용하여 Measurement를 도출합니다. 이때 $g_1$은 Polynomial function, $g_2$는 trigonometric function 등 앞에서 정의한 함수를 사용하며 각 함수는 다른 종류일 수 있습니다. Measurement 수식적인 과정은 아래와 같습니다.

구해진 Measurement를 flatten한 후, 최종적인 decoder $\phi$: $\mathbb{R}^{n \times d} \to \mathbb{R}^{k \times d}$를 통하여 observation을 Reconstruction합니다.

제안 연구에서 Encoder과 Decoder은 MLP layer를 이용하였으며, Encoder 모델은 non-stationary 특성을 직접적으로 학습할 필요 없이 오직 measurement function의 parameter만을 근사하는 것이 목적이다.

• predefined measurement function은 학습된 measurement function을 사용하는 것보다 더 좋은 성능을 보임

[Next]

이어서, (2)편에서 Global and Local Koopman Operators부터 다루도록 하겠습니다!