데이터 분석을 진행할 때 다들 많이 사용하는 알고리즘을 무조건적으로 따라 쓰는 게 아니라, 알고리즘의 한계와 단점을 고민하여 보완할 수 있는 최신 기술들을 학습하는 것이 분석의 폭을 넓혀준다고 생각하여 이번 시리즈를 기획하게 되었습니다. 영어 해석이 부자연스럽더라도 양해 부탁드리겠습니다.
[Introduce]
오늘 리뷰할 논문은 M.Saquib Sarfraz, Vivek Sharma, Rainer Stiefelhagen의 Efficient Parameter-free Clustering Using First Neighbor Relations,
일명 FINCH Clustering입니다.
연구나 데이터 분석을 진행할 때 재현성이라는 개념은 매우 중요하다고 생각합니다. 재현성이란 분석을 진행할 때 나온 결과를 다시 반복하여 따라할 때 역시 똑같이 그 결과가 나오는 것을 의미합니다.
이러한 재현성이 없는 연구는 큰 가치를 지니지 못한다고 할만큼 재현성은 중요합니다. 하지만 대표적인 K-means clustering은 재현성을 지니지 못하며, 기존의 다른 군집화 알고리즘들 모두 군집의 수나 초기 파라미터를 지정해줘야만 했습니다.
(ex. Elbow Method, dendrogram)
이에 군집화 알고리즘을 사용하는 대다수의 분석의 경우 분석가의 주관 내지 재현성 확보를 위한 초기값 설정으로 인해 분석의 객관성을 잃어버리는 경우가 많았습니다.
이에 등장한 FINCH Clustering은 파라미터 지정이 필요하지 않아 객관성을 확보할 수 있는 군집화 알고리즘입니다. 심지어 코드 역시 쉽게 참고할 수 있어 유용한 알고리즘입니다. 그러면 FINCH Clustering을 조금 더 유용하게 사용하기 위해서 논문을 함께 읽어보면서 이해해봅시다.
[논문 요약]
1.Introduction
반백년의 군집화(Clustering) 연구에도 불구하고 아직까지 아래에 대한 보편적인 해결책이 없다.
1) 자동적으로 높은 정확도를 가진 True Clusters를 결정하는 것
2) 데이터에 대한 도메인 지식이나 하이퍼파라미터를 필요로 하지 않는 것
3) 다른 데이터 도메인에서도 일반화할 수 있는 것
4) 매우 큰 데이터(million of samples)를 쉽게 Scale 할 수 있는 것
군집화 기술들은 비슷함의 개념을 잡아줘야한다.
즉, K-means, Agglomerative Clustering, Spectral Clustering 등 현재 존재하는 모든 군집화 기술들은 도메인 지식 등을 통해 '비슷함'을 정의해줘야 한다.
예를 들어 미리 거리 조건이나 하이퍼파라미터를 설정해줘야한다. 하지만 이러한 선택은 주관적이고, 데이터가 바뀌면 바꿔줘야만 한다. 즉, 이러한 파라미터 설정 기반 알고리즘은 불안정하다.
이에 우리는 이 연구에서, 효율적(Efficient)이고 fully parameter free unsupervised clustering algorithm을 통해 앞서 말한 문제점을 해결할 수 있다고 생각한다. 알고리즘이 fully하기 때문에 우리는 파라미터나 군집의 수, 데이터에 대한 도메인 지식을 필요로 하지 않을 수 있다.
2. 선행연구
논문에선 K-means와 affinity propagation algorithm, spectral Clustering, sparse subspace clustering, hierarchical Agglomerative Clustering 등을 관련 연구로 가지고 오며, 이러한 방법들이 모두 Introduction에서 말한 문제점을 가지고 있다고 언급한다.
알고리즘의 자세한 내용을 한번에 모두 살펴보기는 힘드니, 잘 정리된 링크를 첨부한다.
https://jaehc.github.io/ml/affinity-propagation/
(Affinity propagation - 유사도 전파 알고리즘 설명)
https://techblog-history-younghunjo1.tistory.com/93
(Spectral Clustering 쉬운 버전)
https://velog.io/@tobigs-gnn1213/5.-Spectral-Clustering
(자세한 Spectral Clustering)
https://sidneywl2018.tistory.com/33
(sparse subspace clustering)
3. Proposed Clustering Method
역사적으로 군집화 방법은 데이터 포인트 사이의 직접적인 거리를 통해 계산되었으나 고차원의 데이터의 경우 이러한 계산 방법은 Closeness에 대한 정보가 적을 수 있다. (차원의 저주)
Target Manifold의 데이터가 동일하게 분포되어 있는 것은 매우 어렵기 때문에 동일한 Volume으로 계산하고자 하는 위 방법은 실패할 수 있다. 하지만 정확한 거리보단 간접적인 관계에 의존하는 의미론적인 관계(ex. 누가 너의 가장 친한 친구야?)에서는 이러한 문제를 해결할 수 있다.
우리의 목적은 직관적으로 이 의미론적인 관계를 통해 데이터의 군집을 발견하는 것이다.
우리는 각 포인트에서 가장 가까운 포인트들을 관찰하여 데이터 속 연관 관계를 발견하는데 충분한 통계량으로 사용할 수 있다.
그러므로, 각 데이터 포인트들의 Full Matrix를 사용할 필요도 없고, 하이퍼파라미터를 따로 설정할 필요도 없다!!
3-1 The Clustering Equation
이때 은 point 의 가장 가까운 이웃임을 의미한다.
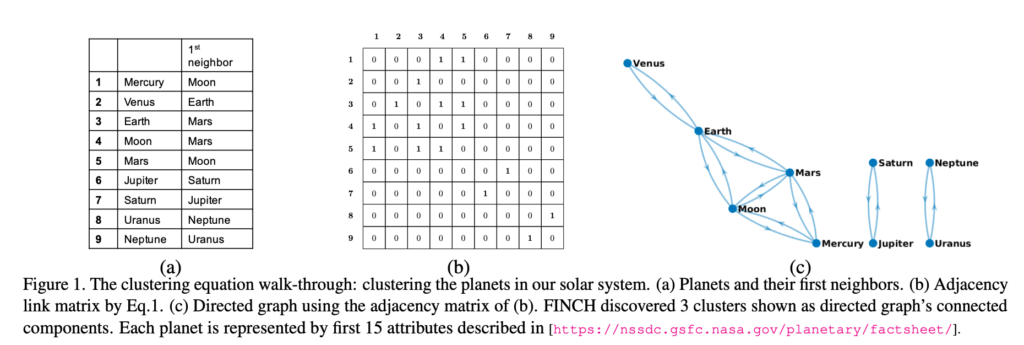
위 Figure를 보면 위 방정식은 추가적인 어떤 분석이나 조건 없이도 군집을 결정할 수 있음을 알 수 있다. 방정식을 이해해보기 위해 위 Figure은 mass, diameter, gravity등 15개의 특성으로 구성된 NASA의 planetary fact sheet에 위 방정식을 적용한 결과이다.
이를 예시로 알고리즘을 설명하자면, Pairwise euclidean distance를 통해 가장 거리가 최소가 되는 Planet의 이웃을 구하여 인접행렬(b)를 계산한다. 이때 인접행렬은 Symmetric이다.
(a)를 보면, Venus의 최근접이웃은 지구이지만, 지구의 최근접 이웃은 Venus가 아니다. 이는 이 방정식을 통해 Chain을 구성하는 방법인데, 조건을 통해 가장 가까운 이웃을 구해준다. 이후 조건을 통해 Mercury와 Mars가 모두 Moon을 최근접 이웃으로, Earth와 Moon이 모두 Mars를 최근접 이웃으로 하고 있으며, 이를 통해 Chain이 형성됨을 알 수 있다. 또한 마지막 조건인 을 통해 Symmetric이 되게 하며 Venus와 같은 데이터들이 Chain을 형성할 수 있도록 이어준다. 이를 통해 위 방정식으로 3개의 군집을 결정할 수 있었다.
3.2 Proposed Hierarchical Clustering
발견한 군집이 데이터의 진짜 군집인지에 대한 분명한 답은 없다. 왜냐하면 군집의 개념은 분석가의 주관적인 의견이기 때문이다.
3.1의 방정식은 자동적으로 데이터들을 군집화하고, 반복적으로 군집을 병합하여 데이터의 내재된 구조를 잡아냄으로써 더 성공적인 군집화를 이뤄낸다. 이때 사용되는 알고리즘은 다음과 같다.

First Integer Neighbor indices we can produce a Clustering Hierarchy, we term our algorithm as FINCH
FINCH의 알고리즘을 간단하게 정리하면 다음과 같다.
- Input: N d인 Sample set을 데이터로 넣는다.
- Output: Sample Set 를 군집화한 까지의 의 Set이 나온다.
- FINCH Algorithm:
- first neighbor인 을 exact distance 등을 통해 계산해준다.
- 주어진 을 통해 과 을 3.1의 방정식을 통해 구해준다.
- 만약 에 2개 이상의 군집이 있다면 다음 과정을 따른다.
- 주어진 데이터 와 로, 군집의 평균을 구해준다. 그리고 이를 통해 새로운 데이터 행렬 을 구해준다.
- 7에서 구한 평균을 기준으로 새 행렬에서의 을 구해준다.
- 새롭게 주어진 를 바탕으로 을 3.1의 방정식을 통해 구해준다.
- ~ 14. 이때 만약 이 하나의 군집이 아니라면 을 로 업데이트해서 6~14 과정을 반복한다.
위 알고리즘 과정을 바탕으로 full distance matrix를 구할 필요없이 가장 가까운 데이터만 얻어서 각 군집의 데이터의 평균을 계산하고 이 평균 벡터로 가장 가까운 이웃을 계산하는데 사용할 수 있다.

또한 군집의 수는 위와 같은 알고리즘을 통해서 계산된다.
- Input: Sample set과 Algorithm 1에서 얻은 를 넣어준다.
- Outpur: 군집의 수를 가진 가 도출된다.
- 에서 까지 아래 과정을 반복한다.
- 주어진 와 를 통해 군집의 평균을 계산하고 새 데이터 행렬 을 구해준다.
- Algorithm 1과 같이 에서의 을 계산한다.
- 주어진 에서 3.1 방정식의 인접행렬을 계산한다.
- 최소 거리인 를 로 두고, 나머지를 0으로 갖는 대칭행렬 를 계산
- 이를 반복하여 의 군집 라벨을 업데이트하여 원하는 군집 수 이 될 때까지 반복
이와 같은 알고리즘을 통한 FINCH 알고리즘은 다음과 같은 성능을 보였다.

이후 4장에서는 주요 모델들과 함께 성능을 비교하고 있으며, FINCH는 특히 Large-Scale dataset에서 좋은 성능을 보인다.
또한 최근 클러스터링 알고리즘을 사용하여 피처 표현을 학습하거나, 딥 모델 훈련을 위한 라벨/의사 라벨을 제공하는 데 초점을 맞추는 deep Clustering에서도 FINCH가 좋은 성능을 보인다.
FINCH를 통해 군집 라벨을 사용하고 이를 딥러닝 모델의 변수로 함께 사용하면 해당 딥러닝 모델이 더 좋은 성능을 보임을 알 수 있다.
[Code]
https://github.com/ssarfraz/FINCH-Clustering
위 링크를 참고하면 자세한 설명을 알 수 있으나, 제가 직접 간단하게 분석에 실시한 결과와 코드를 함께 보여주겠습니다.
부동산의 AVM(Asset Valuation Model)을 모델링하는 과정에서 사용한 예시이며, 데이터는 각 건물의 위경도 좌표만을 사용하였습니다. 또한 적절한 군집화 결과를 위해 위경도 데이터를 표준화하여 사용하였습니다.
다음은 코드와 결과입니다.
from finch import FINCH
c, num_clust, req_c = FINCH(df, distance='euclidean')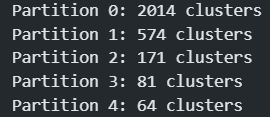
코드에서 c는 행은 input data의 각 군집 label, 열은 계층적 병합 시 각 단계별 군집 label 변화를 의미합니다.
cluster = pd.DataFrame(c)
cluster = cluster.iloc[:, 4]
cluster.name = 'cluster'
cluster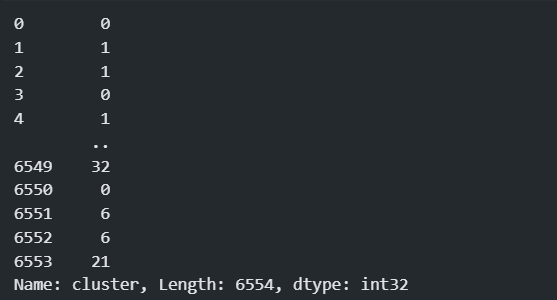
해당 과정에서 저는 가장 Cluster 수가 적은 마지막 단계의 Partition 4를 가지고 왔습니다. 하지만 이는 input data마다 다르니 나중에 활용하실 때 수정이 필요할 수 있습니다.
data = pd.concat([주소, cluster], axis=1)
# 산점도
plt.figure(figsize=(10, 6))
sns.scatterplot(data=data,x ='x',y='y',hue='cluster')
plt.title('Scatter Plot of x and y')
plt.xlabel('x')
plt.ylabel('y')
plt.legend()
plt.grid(True)
plt.show()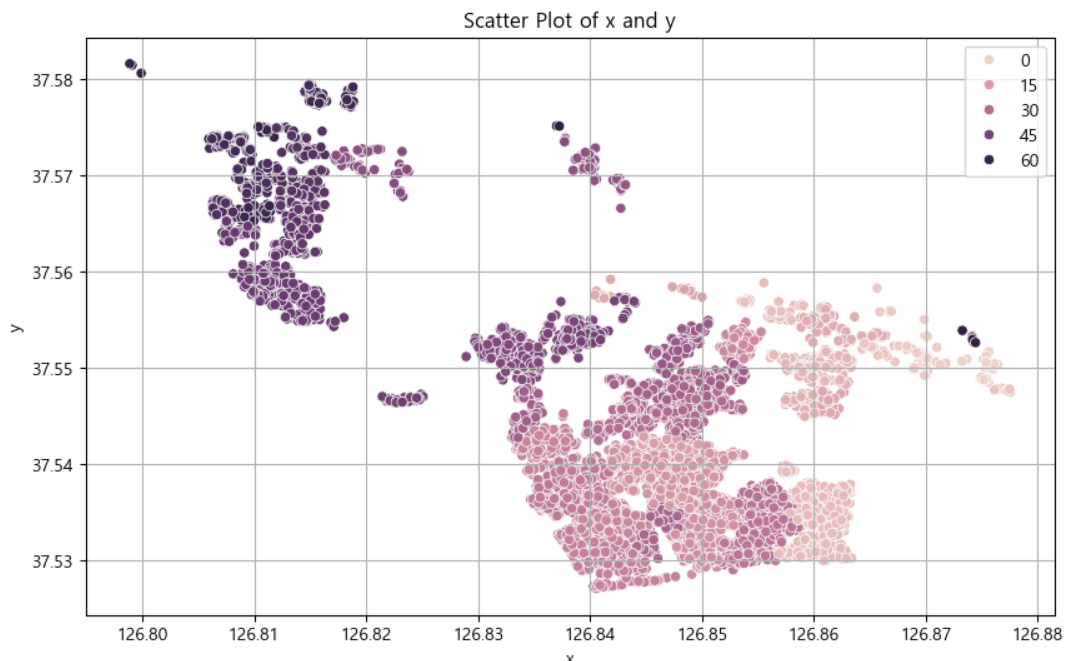
다음과 같이 군집을 만들었습니다.
# 강조할 클러스터 ID
highlight_cluster_id = 19
plt.figure(figsize=(10, 6))
plt.scatter(data['x'], data['y'], color='gray', label='Other Clusters', alpha=0.5)
highlight_cluster = data[data['cluster'] == highlight_cluster_id]
plt.scatter(highlight_cluster['x'], highlight_cluster['y'], color='red', label=f'Cluster {highlight_cluster_id}')
plt.title('Scatter Plot with Highlighted Cluster')
plt.xlabel('x')
plt.ylabel('y')
plt.legend()
plt.grid(True)
plt.show()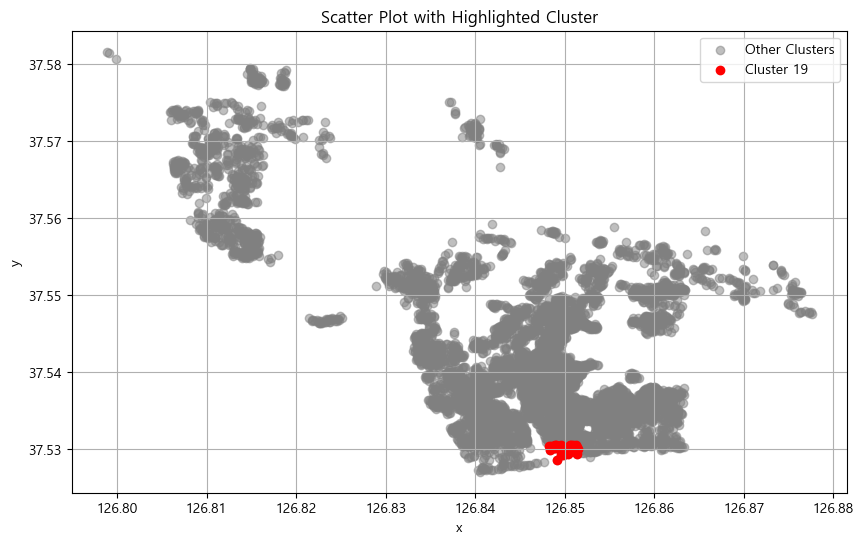
군집 수가 많아서 각 군집 별로 군집화가 잘 이뤄졌는지 확인해보니 위와 같이 잘 나눠졌음을 확인할 수 있었습니다. (해당 코드의 클러스터 ID를 바꿔주면서 확인해보세요!)
[discuss]
이번 FINCH 알고리즘은 군집화의 재현성과 객관성을 확보할 수 있는 매우 좋은 알고리즘이라고 생각합니다. 또한 깃허브에 코드와 예시가 상세히 설명되어 있으며, 코드도 쉬우니 잘 활용하면 분석에 큰 도움이 될 듯합니다. 긴 글 읽어주셔서 감사드립니다.

