5. Spectral Clustering

tobigsGNN·2021년 2월 26일

CS224W Review

목록 보기

5/18

이전 강의에서는 Network의 구조를 분석하고 Network motifs를 찾고 노드간 Community를 찾아내는 방법에 대해 소개했습니다. 이번 강의에서는 이전 내용에 이어 어떻게 그래프를 군집화 하고 더 나아가 Network motifs를 구성하는 Community를 찾아 그래프를 군집화하는 방법에 대해 소개합니다.

1. Spectral Clustering Algorithms

Spectral Clustering을 위한 세 단계를 살펴보겠습니다. 먼저 전처리 단계를 거치고 고유값, 고유벡터를 구한다음 Grouping을 통해 네트워크를 표현합니다. 각 단계에 대해 자세히 알아봅시다.

1-1. Partitioning

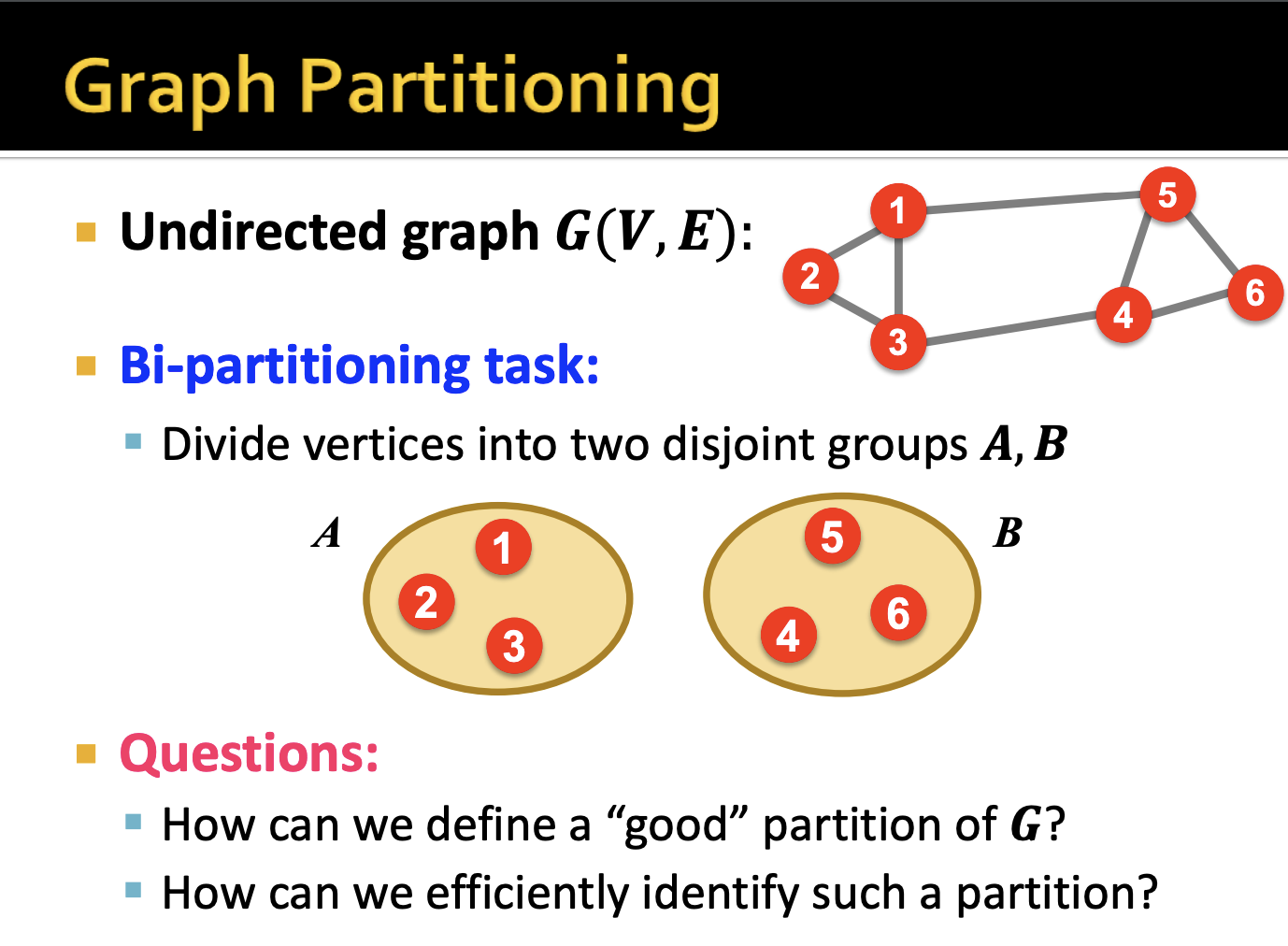
먼저 G라는 Undirected graph가 있다고 가정하겠습니다. 여기서 의문은 우리는 어떻게 노드 1,2,3을 그룹화하고 나머지 노드 4,5,6을 그룹화 하는지입니다. 또한 이런 파티션을 어떻게 알아내는가에 대한 방법도 필요합니다.

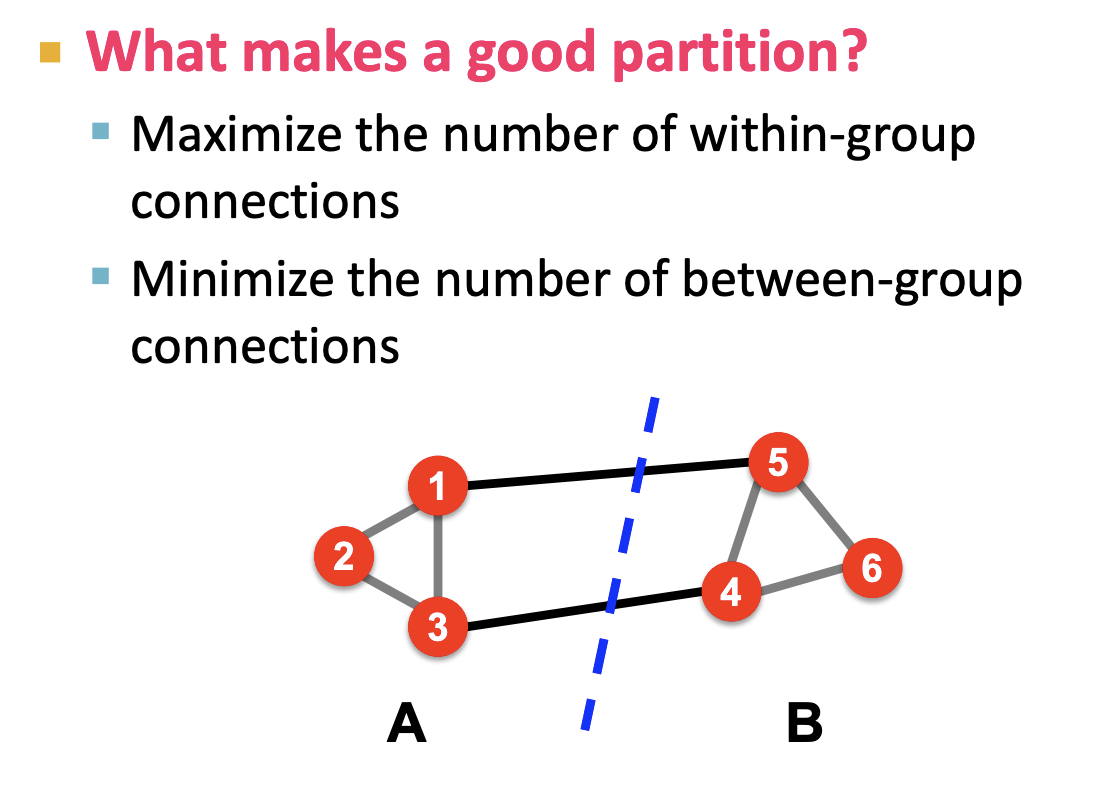
좋은 파티션이라 함은 그룹내 노드간 간선이 최대며 그룹간의 간선이 최소여야 합니다. 이전 강의에서 Modularity를 배웠는데 이와 비슷한 개념이라고 이해했습니다. 결국 강한 연결을 지닌 서브 네트워크를 식별하여 분리합니다.

1-2. Edge cut

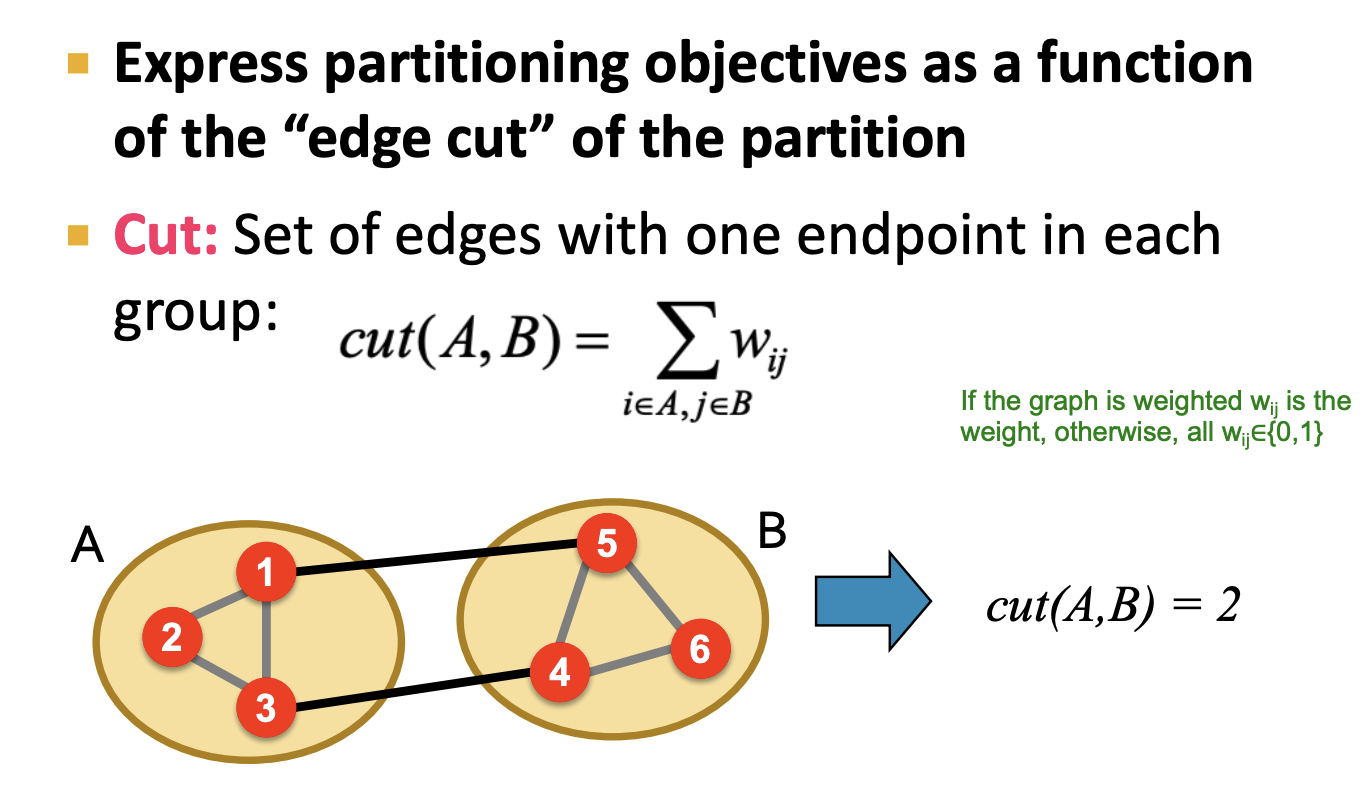
파티션을 표현하는 목적함수로 edge cut을 사용합니다. 이는 각 그룹에서 종점이 있는 간선 수로 나타낼 수 있습니다. 위 그림에서는 파티션 A, B에 대한 edge cut은 2입니다.

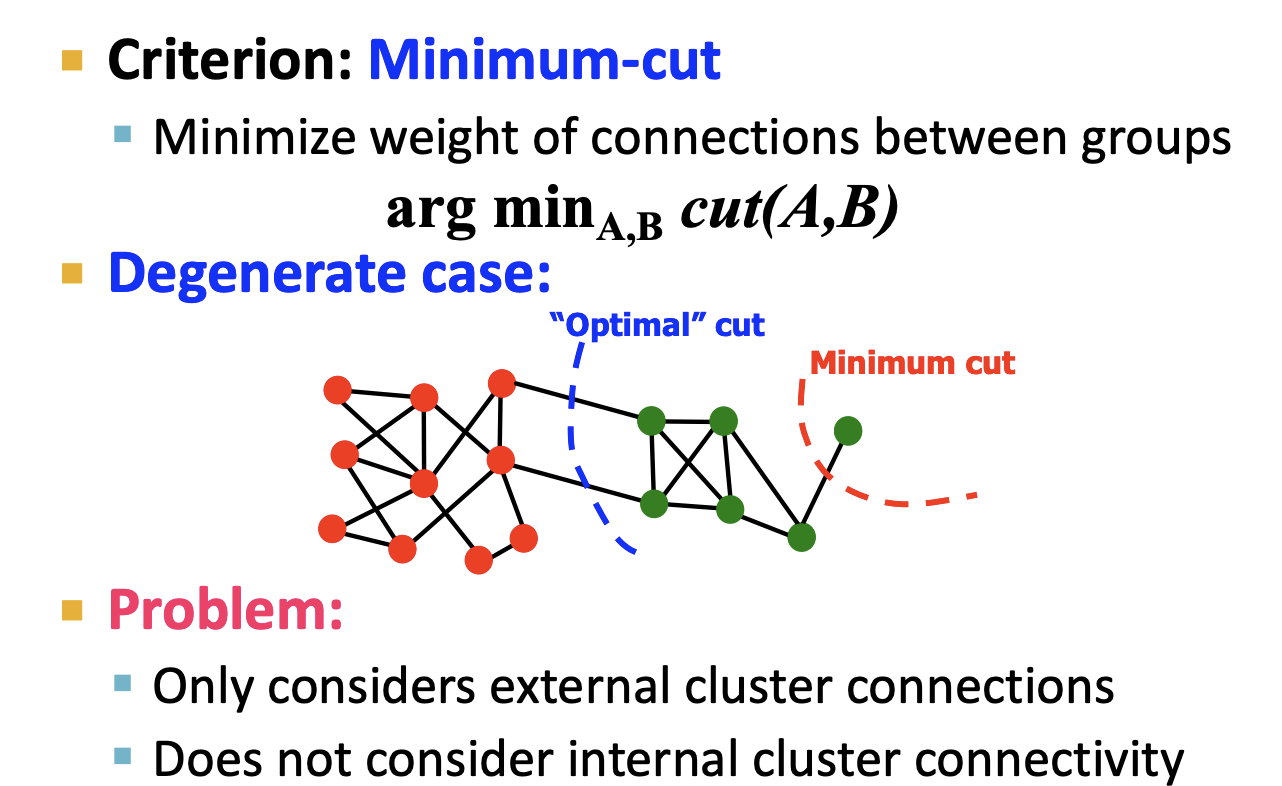
그래서 우리가 하려는 것은 두 파티션에 대한 최소 edge cut를 얻는 것입니다. 위 그림에서 Optimal cut을 찾는 과정이라고 할 수 있습니다. 하지만 이는 오로지 군집간의 연결만 고려하였고 군집 내부의 연결성에 대해선 전혀 고려하지 않았습니다.

1-3. Conductance

edge cut 대신 우리는 Conductance를 사용합니다. 군집간 연결성을 비교하는데 각 군집의 밀도를 반영합니다. edge cut값이 작고 min(vol(A), vol(B))의 값이 커진다면(=두 군집의 밀도가 유사) 작은 Conductance값을 얻을 수 있습니다.
이전에 좋은 파티션을 어떻게 알아내야하는지에 대해 얘기했습니다. 답은 최소 Conductance값을 구하는 것입니다. 하지만 이는 NP-hard 문제로 최적의 파티셔닝을 구하기 위해 Conductance값을 계산하는것은 쉽지 않습니다.
NP-hard: 대표적으로 TSP(Traveling Salesman Problem)문제가 있습니다. 그래프내 간선을 전부 비교하면서 문제를 해결하는 방법으론 다항시간내에 풀 수 없습니다. 이러한 NP-hard문제를 해결하기 위해서 휴리스틱한 방법이나 가지치기, 탐욕법등의 방법을 적용합니다.
이후 내용에서는 그래프에서 얻은 행렬, 고유값, 고유벡터를 통해 파티셔닝을 하는 방법에 대해 소개합니다.

1-4. Spectral Graph Partitioning

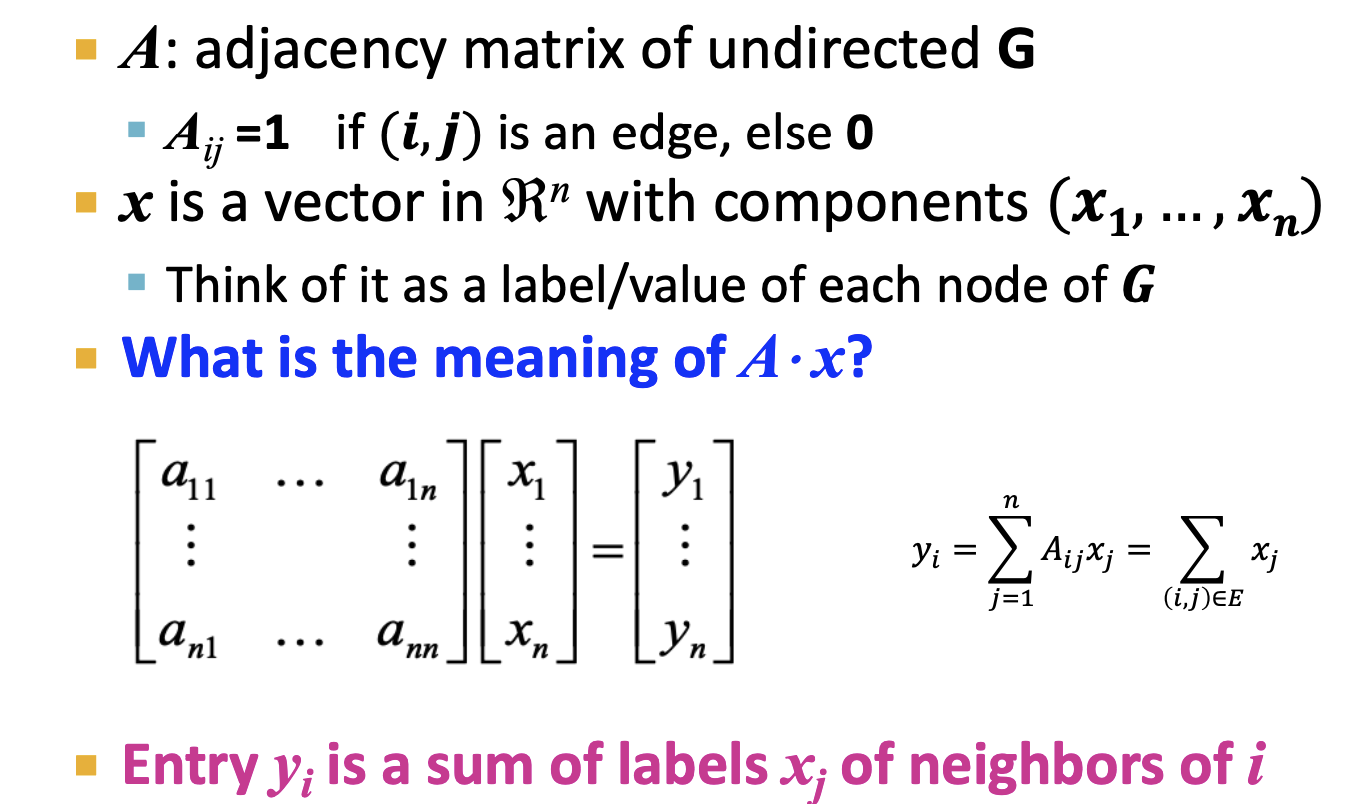
Matrix A : 그래프 G에서 얻은 인접행렬. 노드 i,j가 연결되어 있다면 1, 아니면 0을 가집니다.
y : 우리는 인접행렬에서 x 벡터를 곱하여 y 벡터를 얻었습니다. y벡터는 각 노드가 이웃한 총 노드 수를 표현합니다.

여기서 고유벡터와 고유값이 등장합니다.

그래프 G의 모든 노드들이 차수 d를 가지는 d-Regular Graph의 경우를 살펴보겠습니다.
여기서 가장 큰 고유값은 d입니다. CS230n Lecture7 의 내용을 빌리자면 이런 가정을 하는 이유는 원하는 결과를 보기 위함이라고 설명했습니다. Deconvolution case를 예를들어 설명하겠습니다.

실시간으로 이미지에서 object detection하는 모델이 있다고 가정합시다.
일반적인 CNN를 보면 이미지의 feature extraction을 통해 낮은 차원을 가진 정보를 반복적으로 가지고갑니다. 실제로 Convolution Layer은 이미지 전체를 보지 않습니다. 커널이 지나가는 이미지의 일부분에서 계산된 값을 다음 정보에 저장합니다.
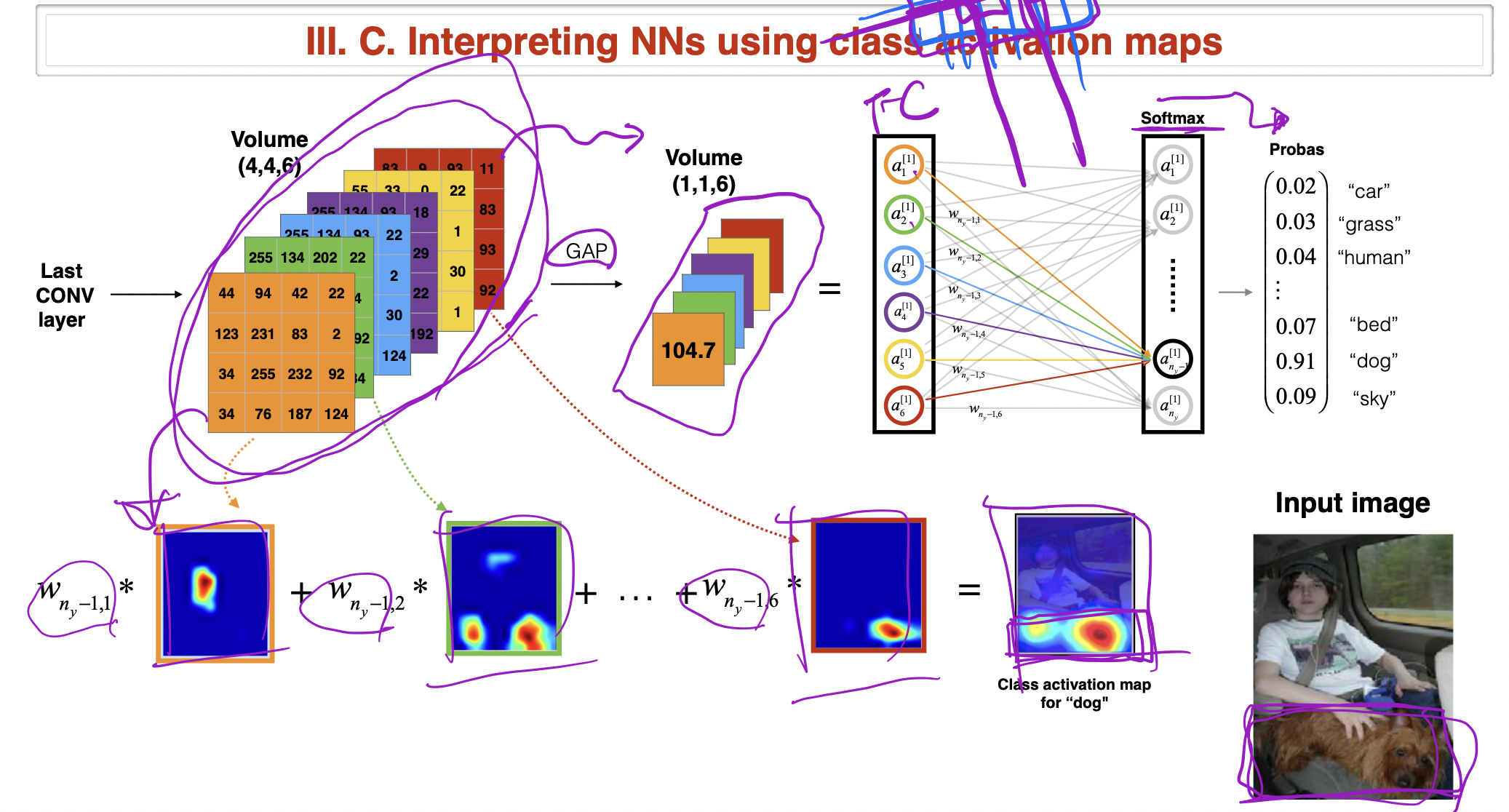
위 그림과 같이 실제로 Convolution Layer을 통해서 나온 값을 확인해보면 해당 object일 확률이 높은 region을 표시하면 다음과 같은 사진이며 이 값들이 Fully Connected layer의 가중치와의 곱과 합을 통해서 Classification을 진행합니다.

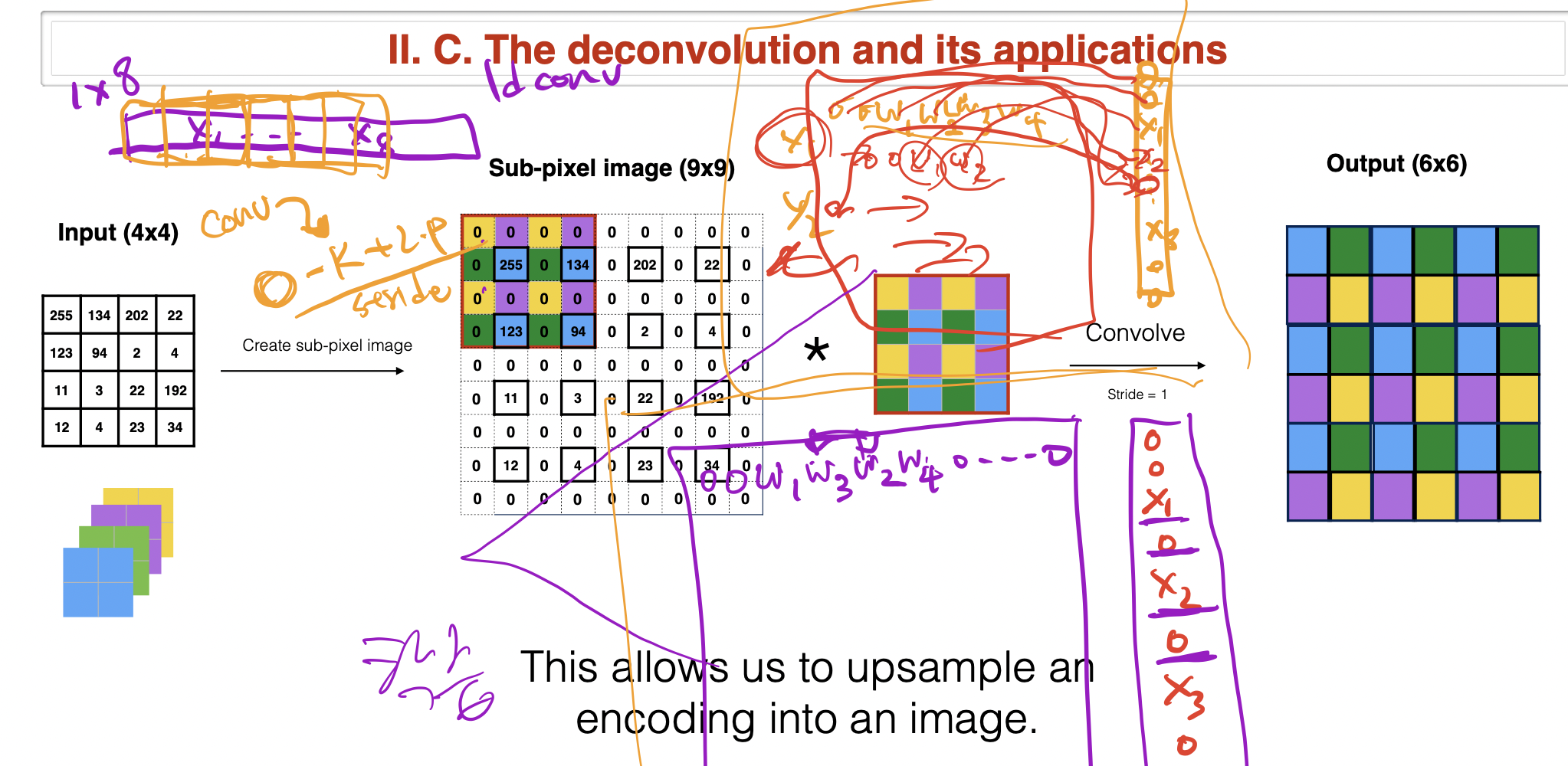
여기서 복원 벡터가 있다고 가정하고 Deconvolution을 통해서 해당 값이 어떤 이미지의 부분을 집중적으로 보았는지 복원해봅니다. 강의에서는 이런 가정을 통해서 우리가 하려는게 정말 가능한지를 확인하기 위해서 한다고 합니다. 사실 학습을 한다면 이런 가정이 무의미하다고 설명합니다.

그래프 G가 위 사진처럼 C와 B 파티션을 두 가지 경우로 가진다고 가정하겠습니다.
왼쪽의 경우 C, B 파티션이 연결성이 없으므로 최대 고유값과 두번째로 큰 고유값은 동일합니다. 이전 페이지에서 x가 전부 1인 고유벡터와 최대 고유값을 가짐을 확인했습니다.
다시 돌아와서 x벡터가 C 파티션의 노드 정보만 가지는 경우와 B 파티션의 노드 정보만 가지는 경우를 생각해보면 고유값이 동일함을 알 수 있습니다. 오른쪽의 경우 C, B 파티션이 연결성을 가진다면 근사한 값을 가지지만 동일하진 않습니다.

여기서 오른쪽 경우가 d-regular graph라고 가정하겠습니다. 그러면 이미 아는대로 모든 값이 1인 고유벡터가 최대 고유값을 가집니다.
고유벡터들은 직교함으로 서로 곱하였을때 0이 나와야합니다. 그러면 다른 고유벡터의 모든 값들의 합은 0이 되어야 합니다. 그렇다면 두 그룹의 노드정보에 대해 양수, 음수의 그룹으로 나누어 표현하게 됩니다.

1-5. Matrix Representations

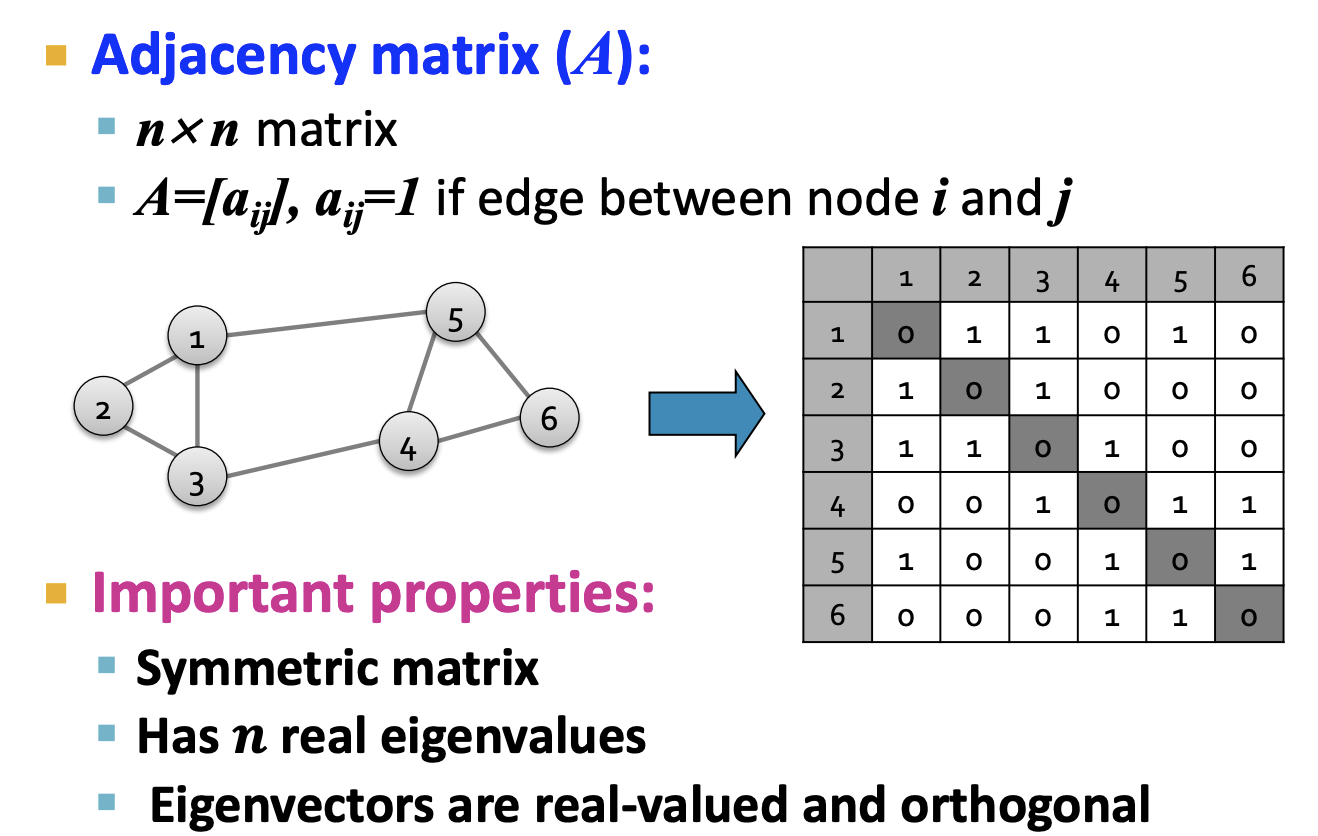
1-6. Laplacian Matrix

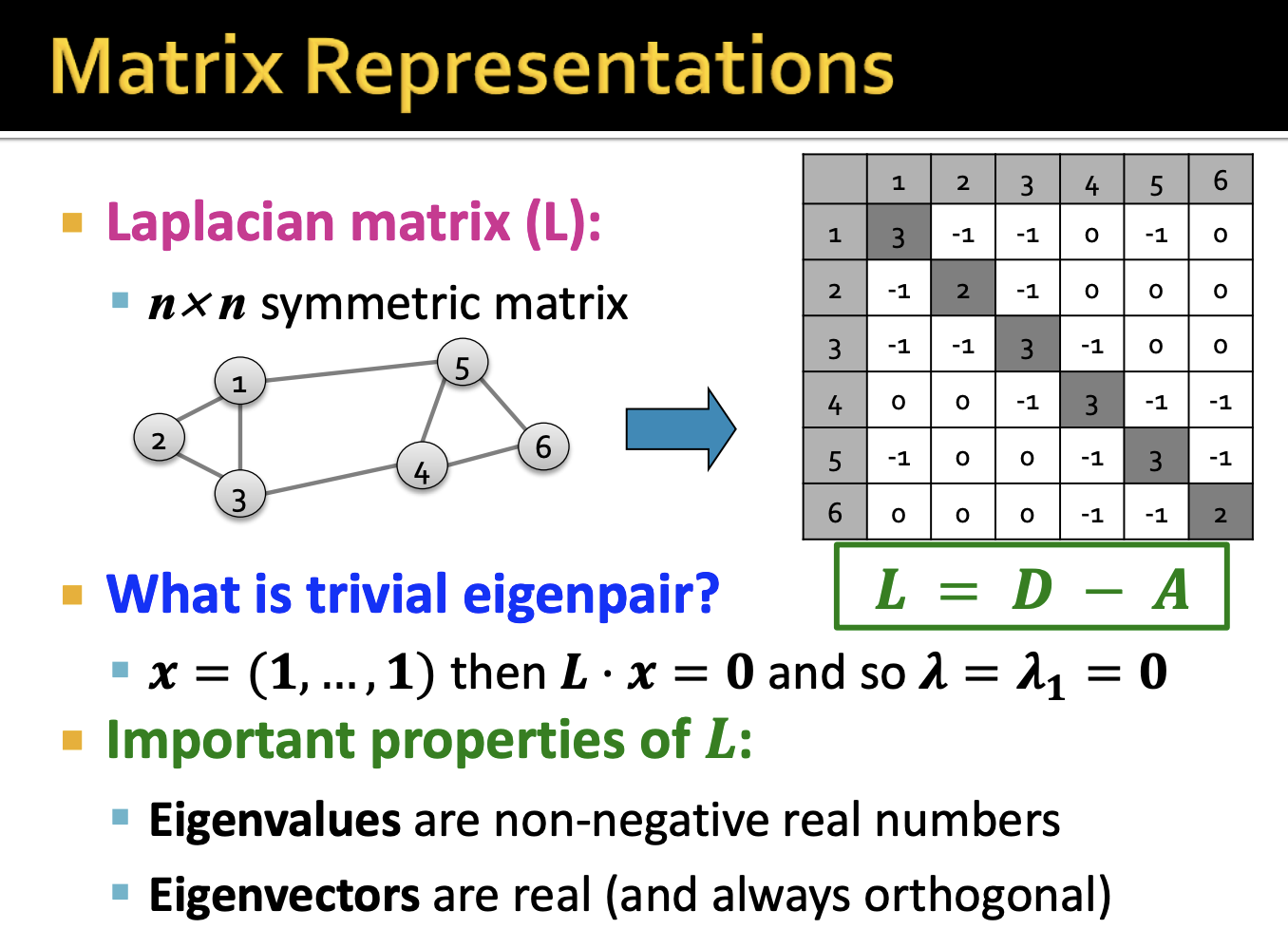
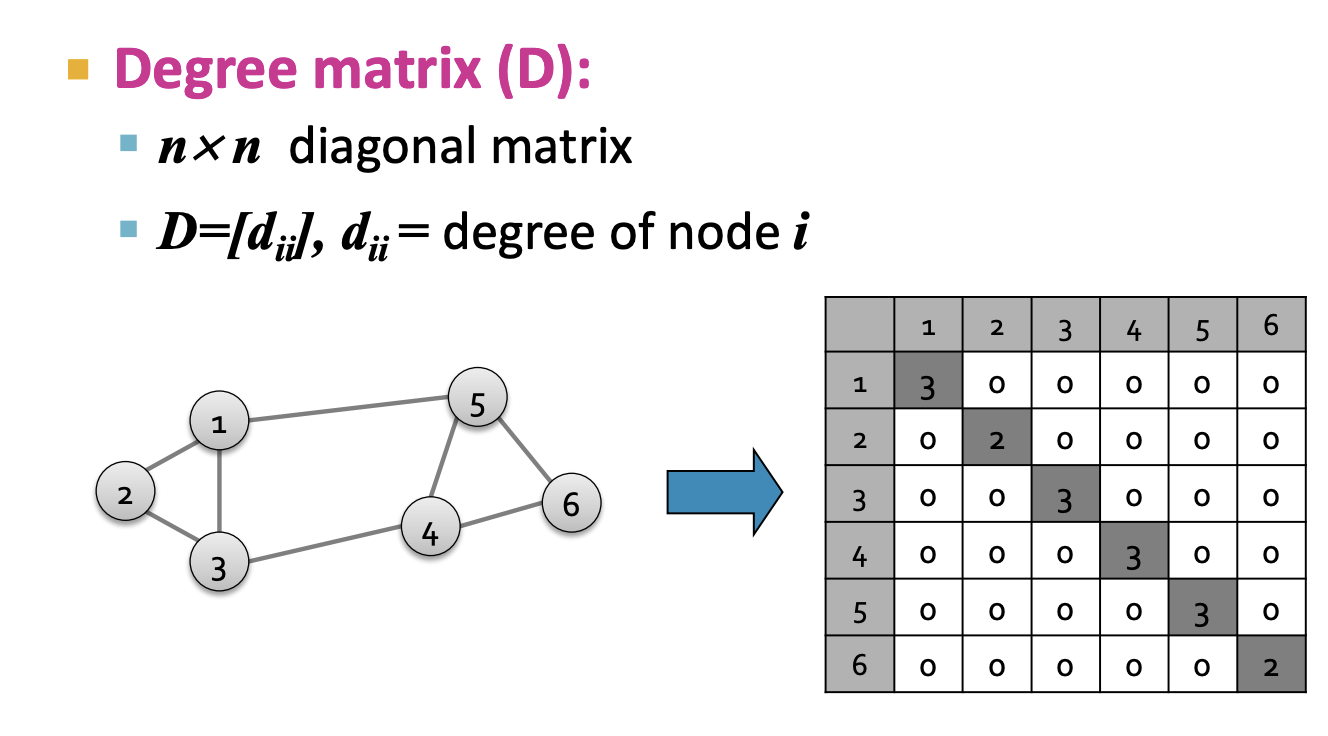
위에서 차례대로 인접행렬 A와 차수행렬 D를 보았습니다. 여기서 Laplacian Matrix L은 D - A로 표현할 수 있습니다.
여기서 모든 L의 값의 합은 0입니다. 그래서 이전과 동일하게 모든 값이 1인 고유벡터는 최대 고유값을 가지는건 자명합니다.

1-7. Rayleigh Theorem

여기서 우리가 구하고싶은 람다2를 통해서 그래프를 파티셔닝합니다.
수식을 정리하면 노드 i, j 차이의 제곱합임을 알 수 있습니다.

여기서 y벡터가 A, B파티션에 속하는 노드에 대한 정보를 담고있는데 A에 속하면 1, B에 속하면 -1이라고 합시다. 그러면 우리는 군집내 노드와 다른 군집의 노드만 고려하면 됩니다.
여기서 람다2는 최소 값의 f(y)로 표현할 수 있습니다. 그리고 고유값에 대응되는 고유벡터를 x로 두고 있습니다.
정리하자면 이 x 벡터가 군집을 결정하고 Conductance를 최소화 합니다.

1-8. Summary

그래서 우리는 지금까지 그래프의 좋은 파티션의 정의를 하였고 이를 찾는법은 cut criterion(=conductance)를 최소화하는 것이었습니다.
파티션을 찾는 좋은 방법은 그래프에서 얻은 행렬에서 고유값, 고유벡터를 사용하여 추정하는 것입니다.

우리는 지금까지 Spectral Partitioning Algorithm에 대해 살펴보았고 총 정리를 하겠습니다.
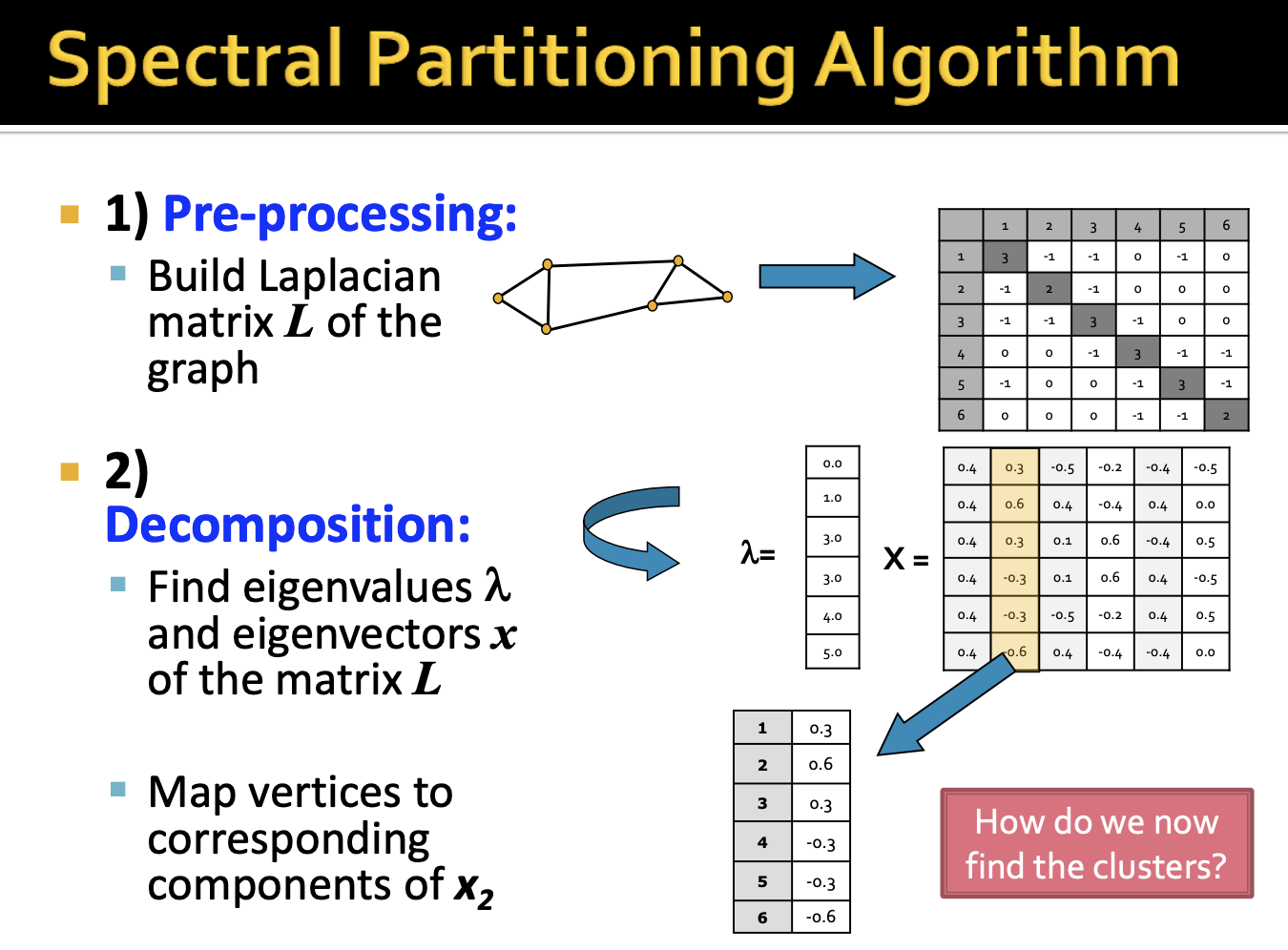
먼저 Pre-processing단계에서 그래프의 인접행렬과 차수행렬을 통해 Laplacian 행렬을 얻습니다.
Decomposition을 통해 Laplacian 행렬의 고유값, 고유벡터를 구합니다. 우리가 집중해야할 값은 람다2 입니다.
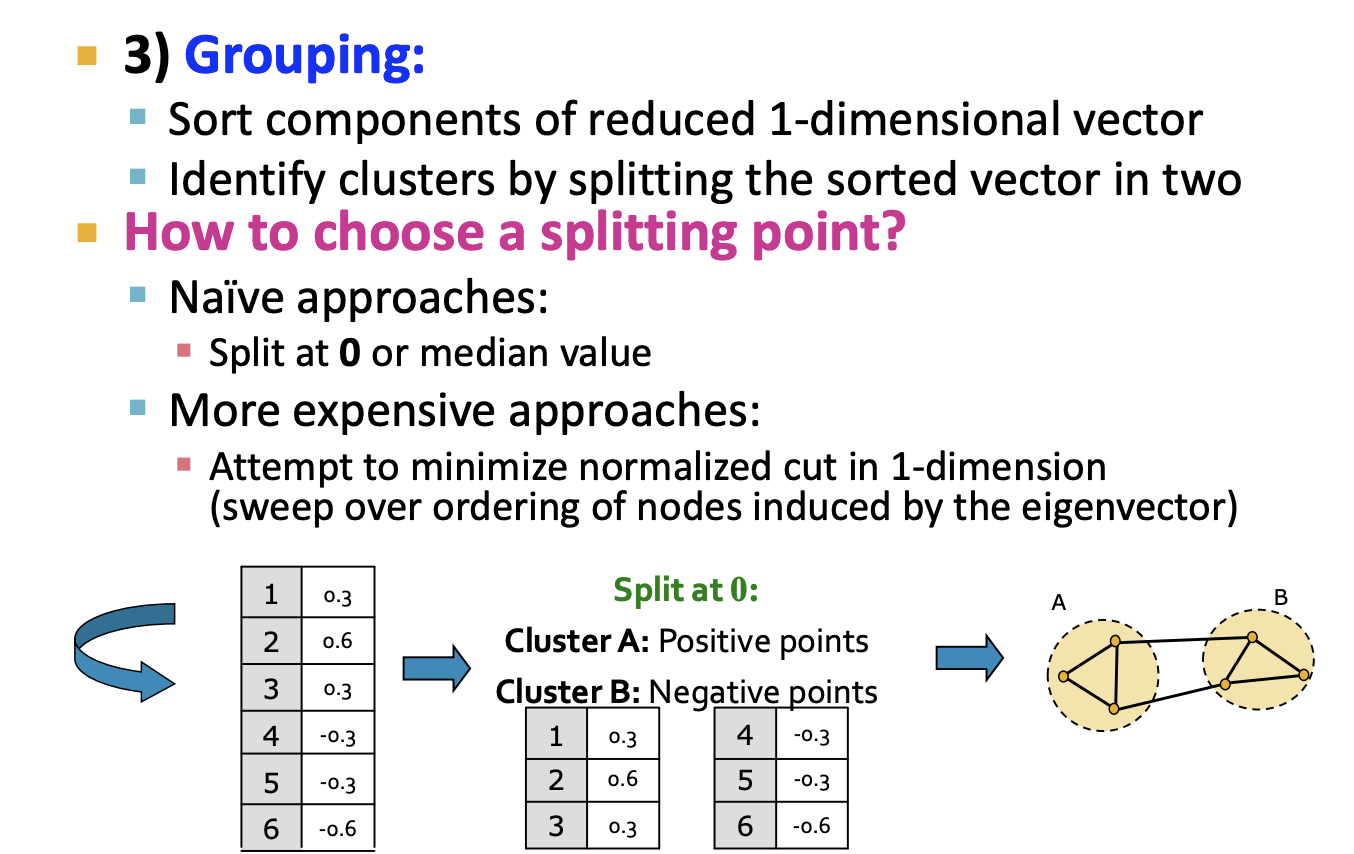
이전 단계에서 얻은 고유벡터에 담긴 노드 정보로 Grouping을 하여 파티셔닝을 진행합니다. 여기서 나이브하게 접근하면 0 또는 중간값으로 분리하여 파티셔닝을 하고 벡터내 값을 정규화하여 노드의 파티션을 정한다고 합니다.

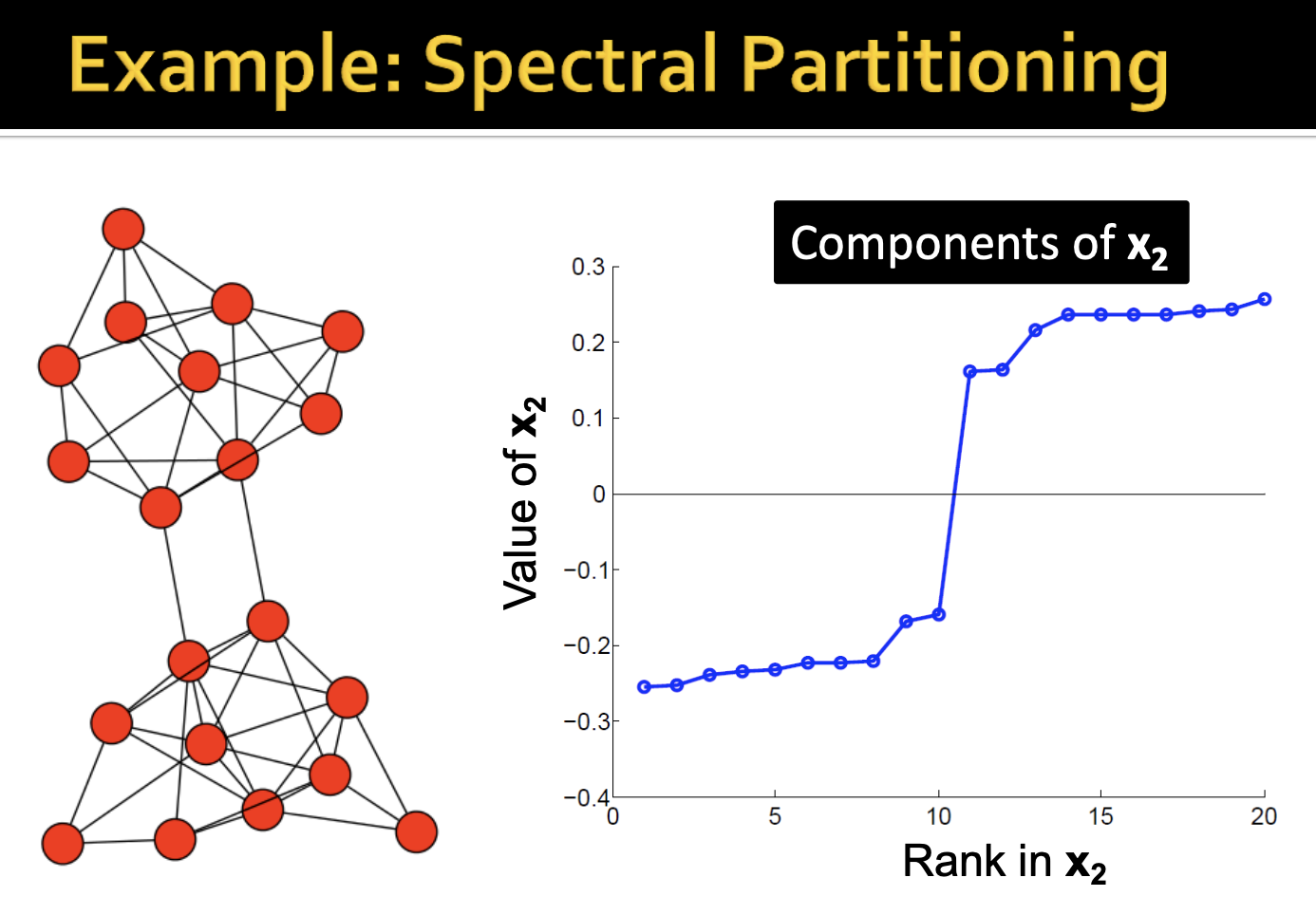
-이렇게 파티셔닝한 결과를 보겠습니다. 오른쪽 그래프에서 0을 지나는 구간을 자릅니다. 그리고 가장 0에 가까운 노드 4개는 왼쪽 그래프의 네트워크의 게이트웨이 위치에 있음을 확인할 수 있습니다. 오른쪽 차트가 나타내는 그래프 정보가 왼쪽 실제 그래프와 일치함을 볼 수 있습니다.

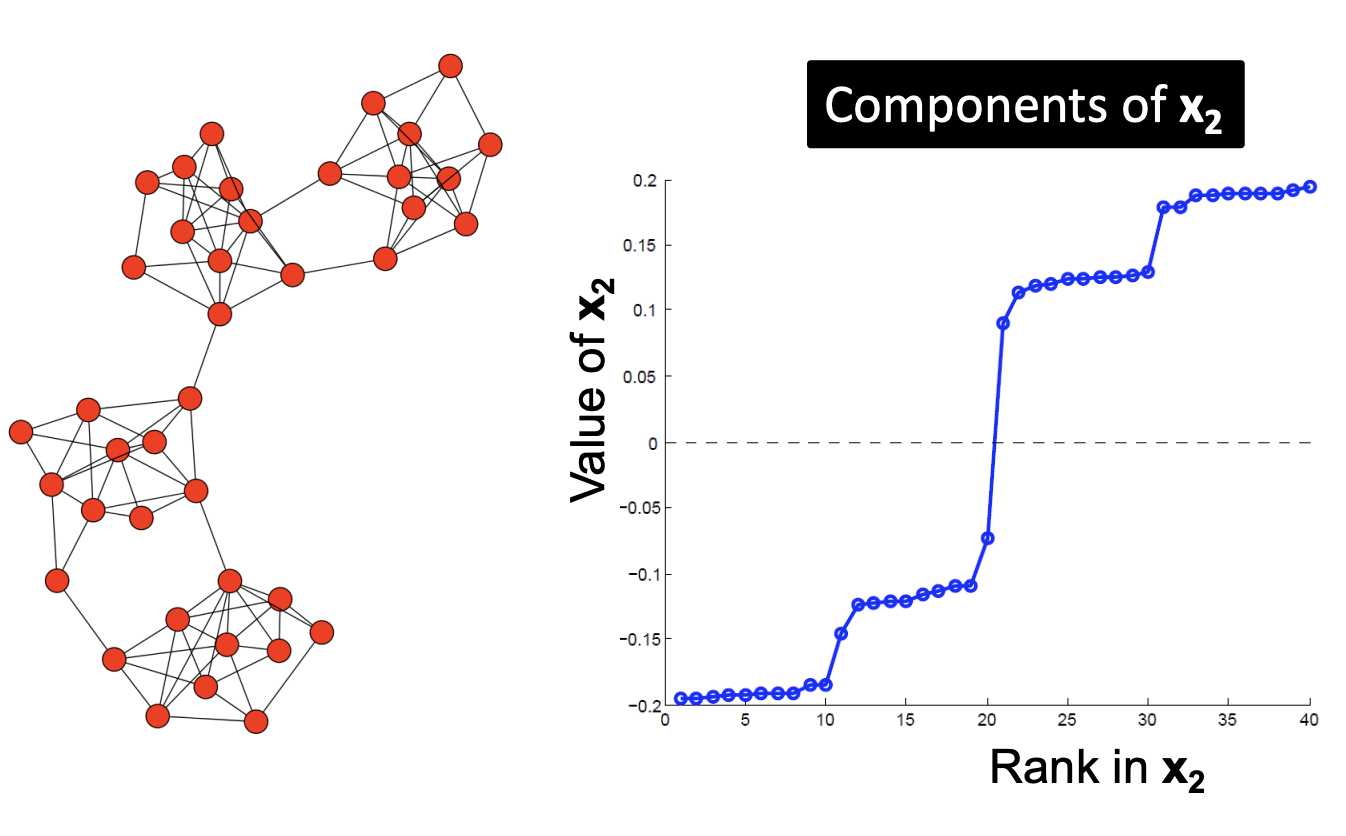
다음의 경우를 보겠습니다. 0을 지나는 구간은 왼쪽 그래프의 서브 그래프를 연결하는 간선을 의미합니다.

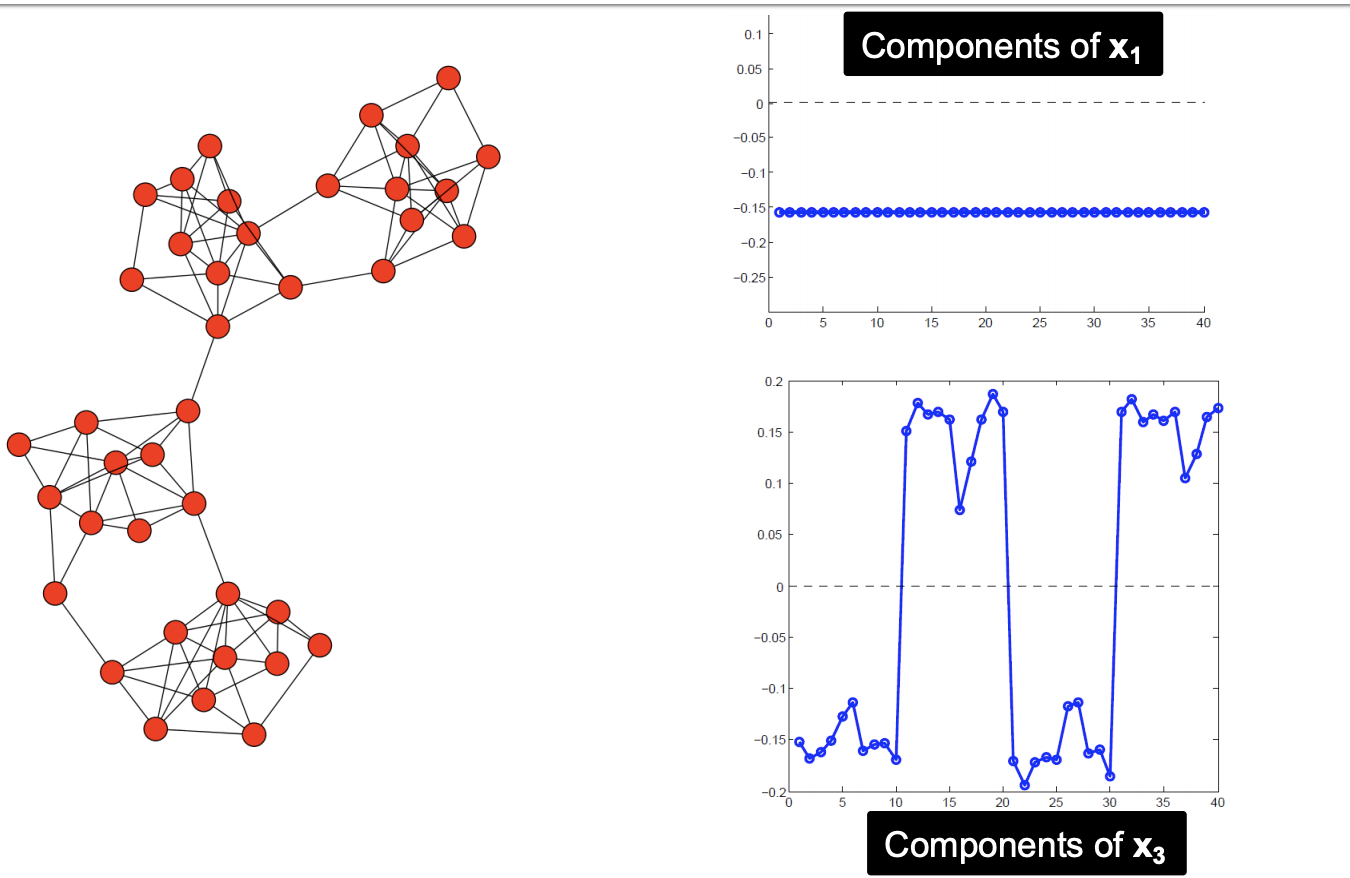
다른 람다값의 벡터에 대한 결과입니다. 람다1은 모두 같은 값을 가집니다.

1-9. K-Way Spectral Clustering

군집의 수를 정하는 이 k 변수를 어떻게 정해야하는지에 대해 방법을 제시하고 있습니다. PCA에서 고유값, 고유벡터를 사용하는것과 유사하다고 이해했습니다.

연속한 두 고유값의 차이가 가장큰 경우의 k를 선택합니다.

2. Motif-Based Spectral Clustering

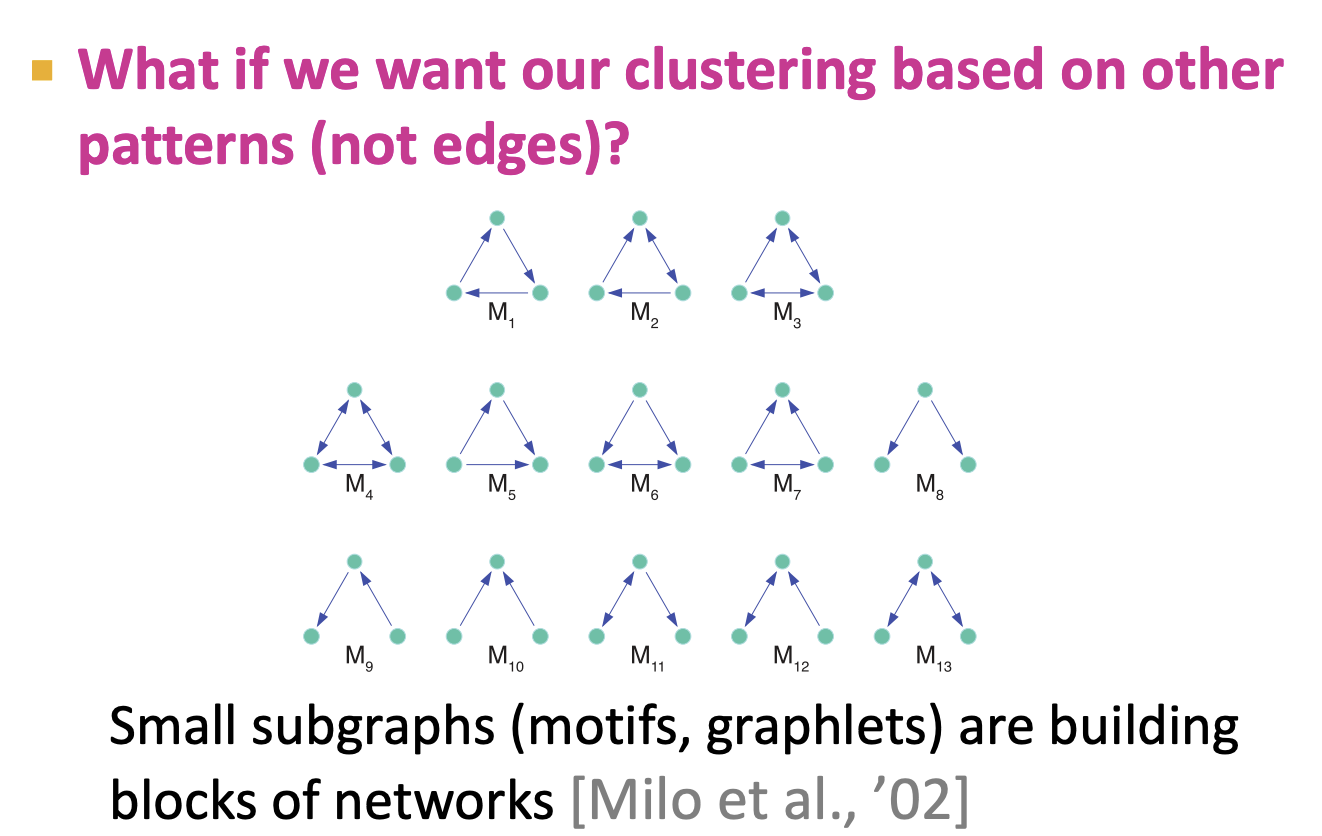
파티셔닝을 하는데 Network motifs를 바탕으로 할 수 있는지가 main discussion입니다.

2-1. Modules of Motifs

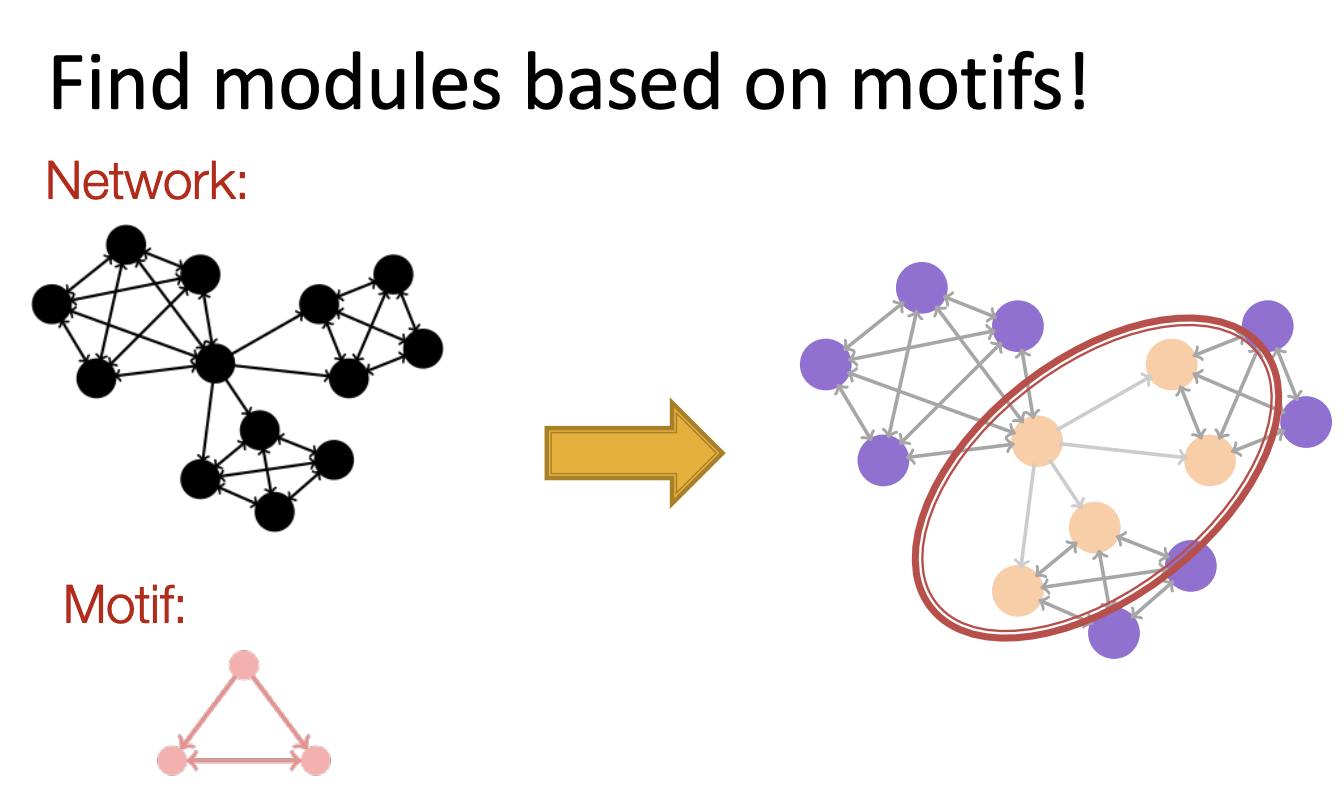
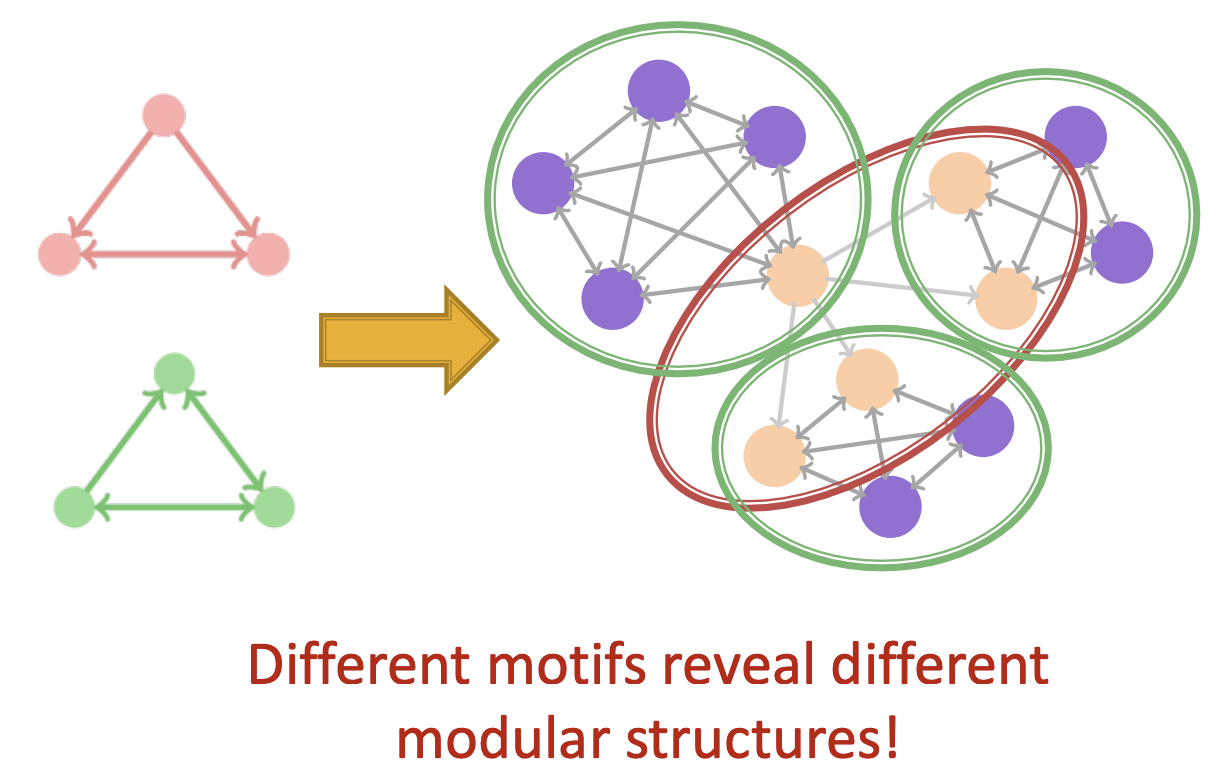
Based Motif에 따라 다르게 파티셔닝됨을 볼 수 있습니다.

2-2. Motif Conductance

이전까지 우리는 edge cut에서 conductance 개념을 살펴보았는데 이를 motifs 관점에서 적용시켜 다루겠습니다.

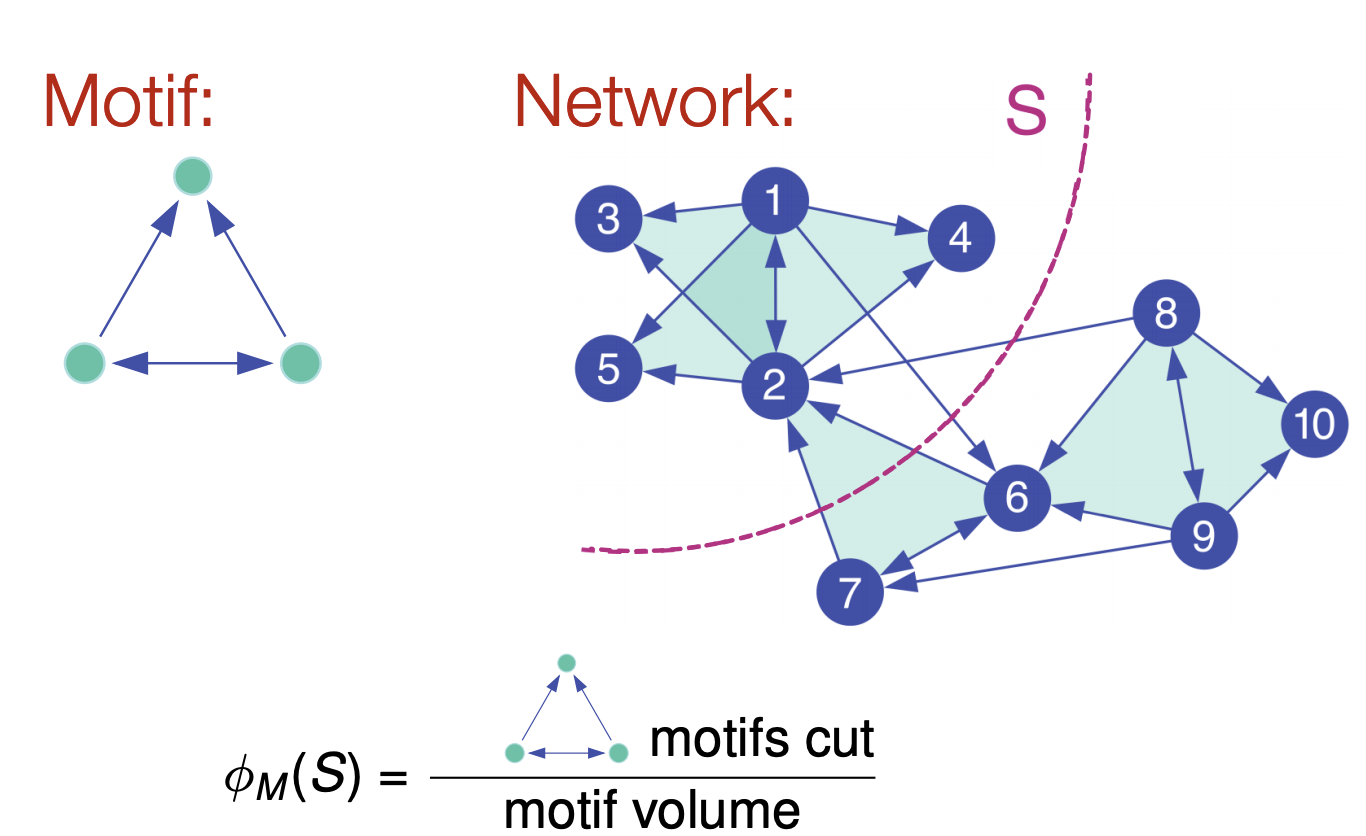
전체 네트워크에 6개의 motif를 볼 수 있습니다. 그리고 cut을 기준으로 4개의 간선이 존재하는데 두 간선은 motif를 이루는 간선이 아님으로 제외합니다. 그렇다면 파티셔닝된 S 네트워크의 motif volume은 2번 노드를 기준으로 4개의 motif가 존재하고 3개의 완전한 motif와 2번 노드만 남은 motif가 있음으로 10입니다. 여기서 잘린 motif는 하나 임으로 S 네트워크 Motif Conductance는 10 / 1로 정의할 수 있습니다.
이 과정 또한 NP-hard문제 입니다. 이전 Spectral Clustering Algorithm을 적용하겠습니다.

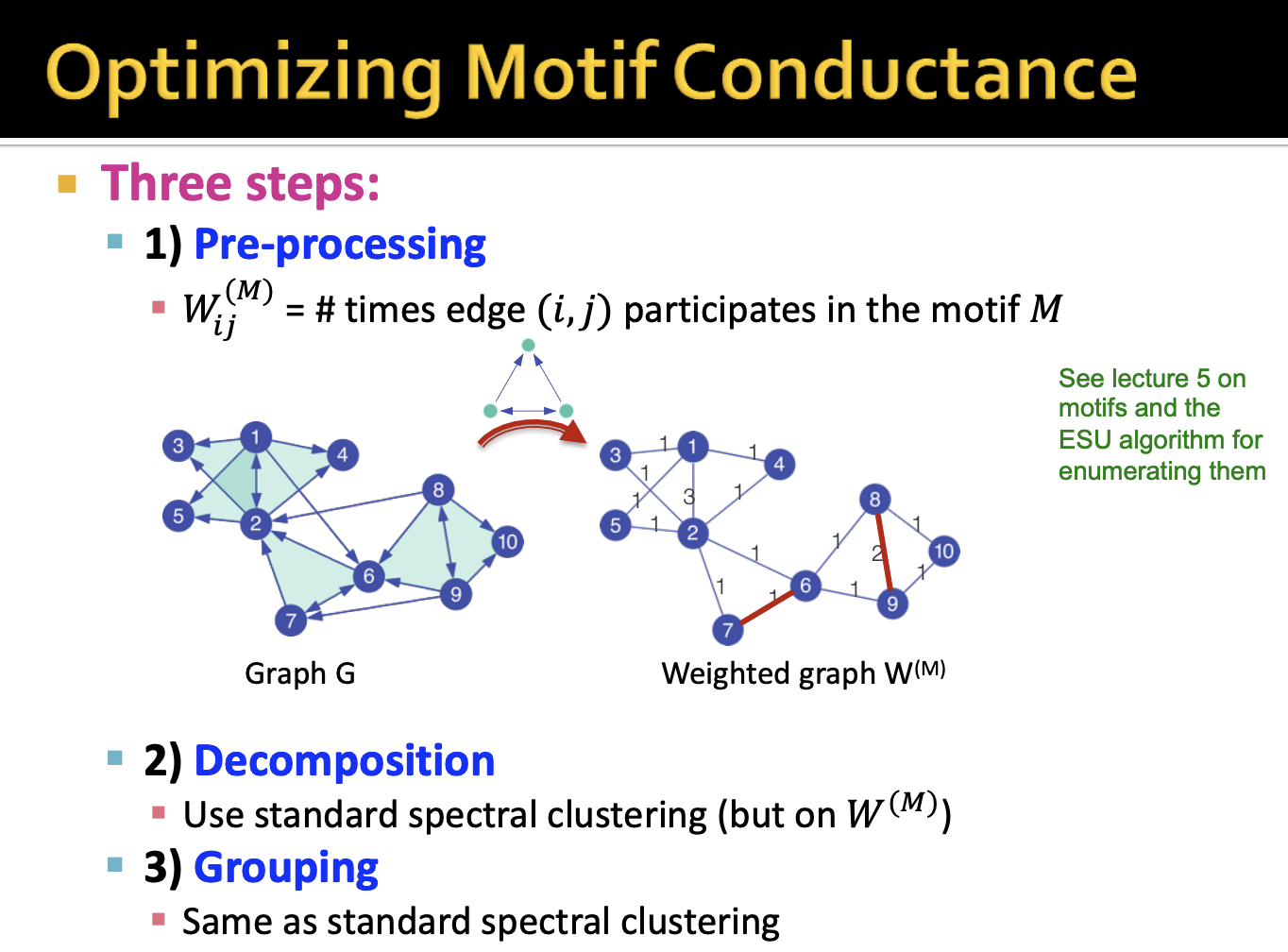
Spectral Clustering Algorithm 의 단계와 동일합니다. 하나씩 살펴보도록 하겠습니다.

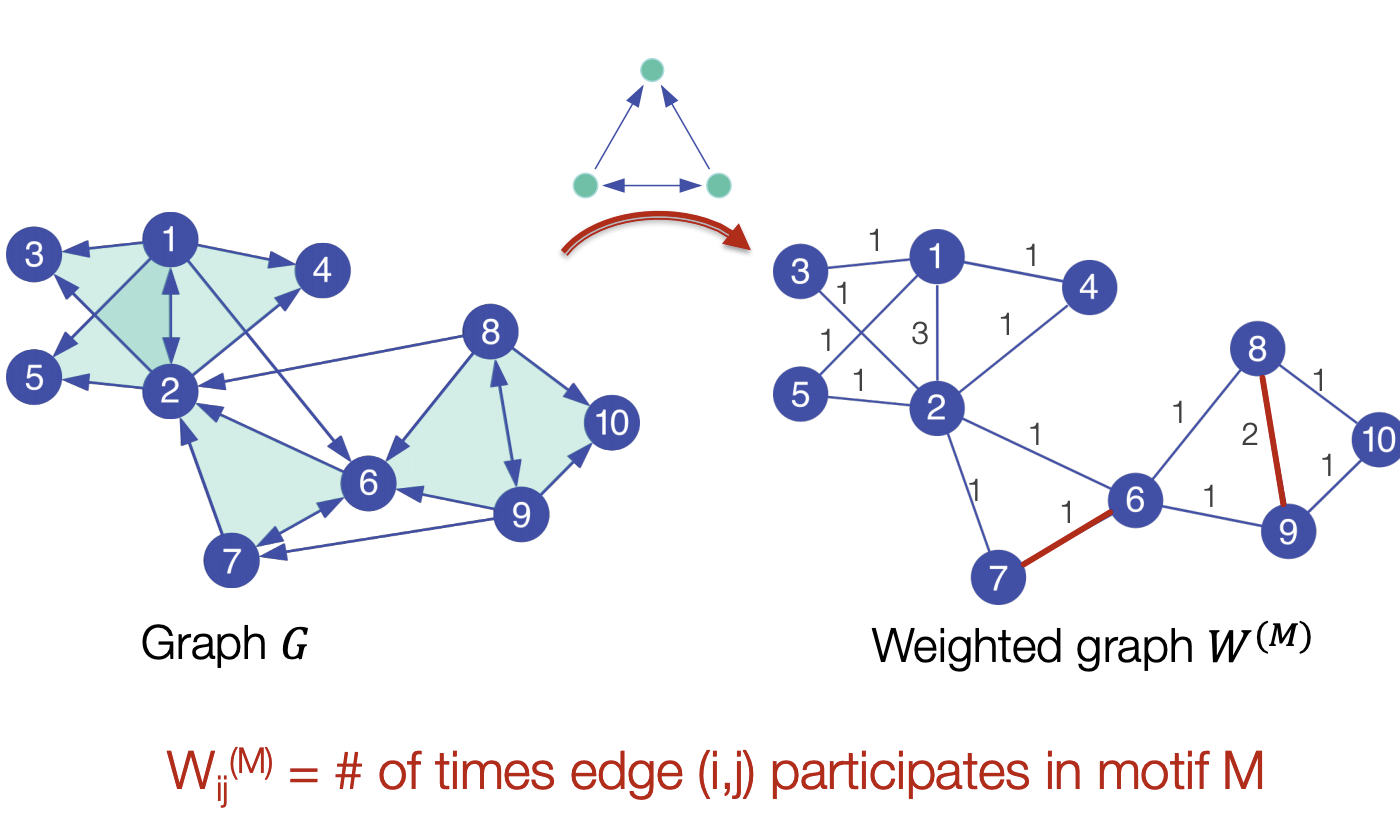
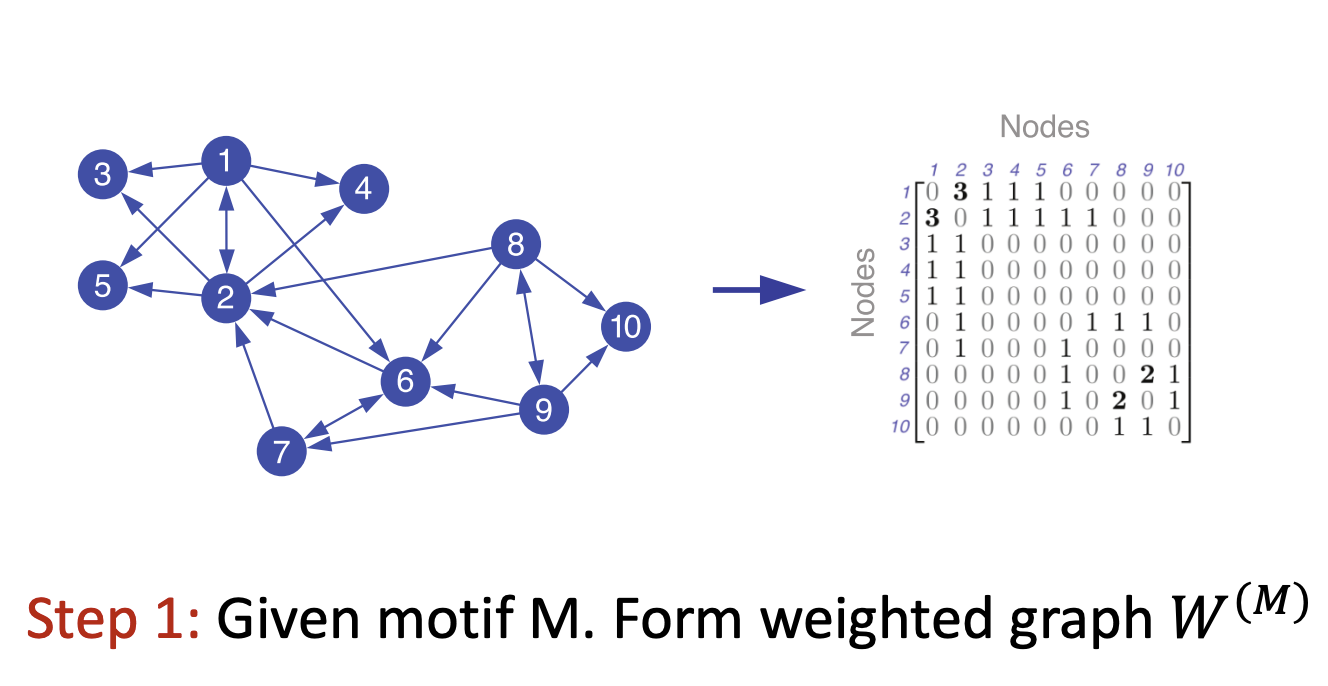
주어진 motif에 대해서 motif를 이루는 서브 그래프를 찾고 간선에 가중치를 주는 Matrix W를 둡니다.
Matrix W는 low motif conductance를 찾도록 합니다.

이어서 Laplacian Matrix를 구합니다. 이전에는 인접행렬을 사용했다면 이번엔 W 행렬을 사용합니다.

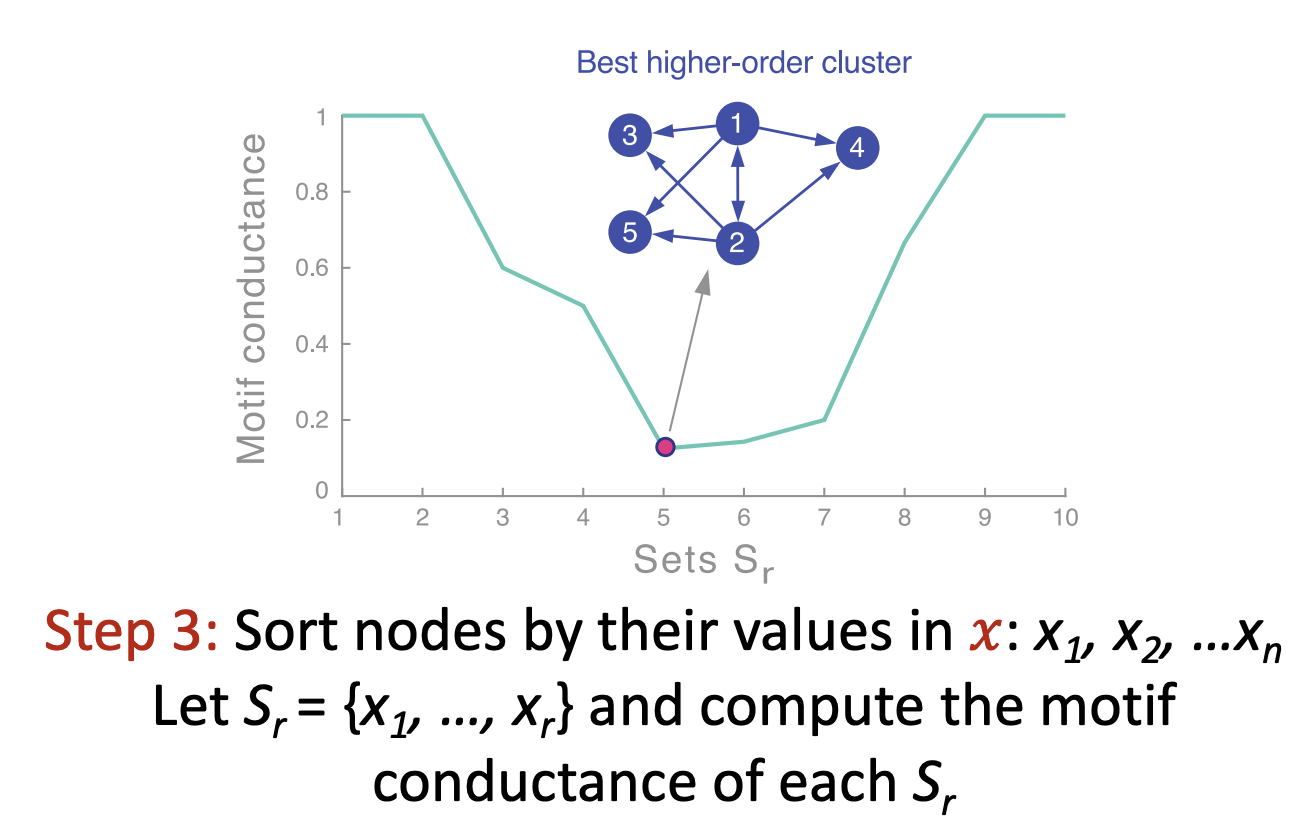
람다값을 구하고 이에 상응하는 고유벡터를 얻습니다. 여기서 최소 Motif Conductance를 띄는 노드의 정보를 통해 Grouping 과정을 진행합니다.

2-3. Motif Cheeger Inequality

Motif conductance가 다음과 같은 값의 범위를 가진다고 설명하고 있습니다. 이는 앞서봤던 람다2와 유사하다고 이해했습니다.

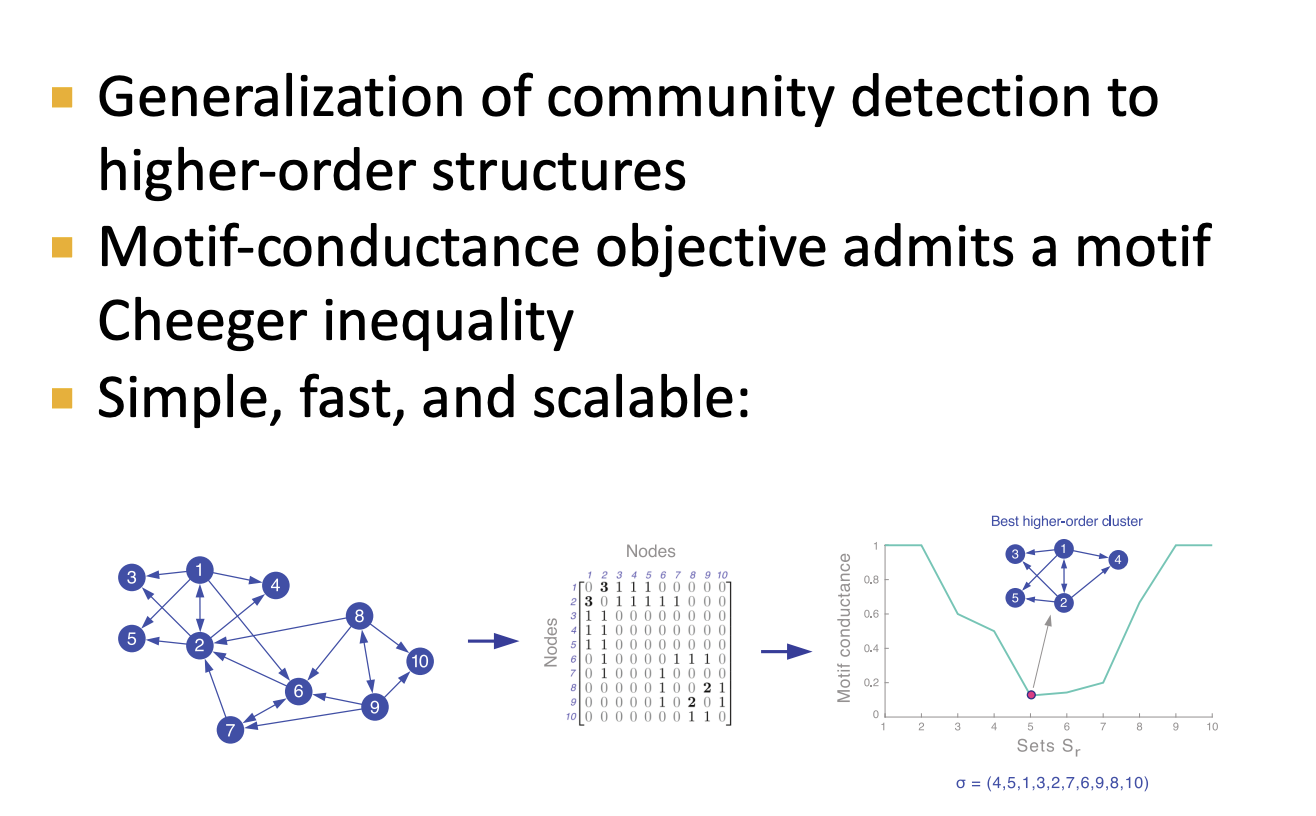
정리하자면 최적의 Motif conductance은 위의 정리를 따르고 값을 구하여 Motif를 기반으로한 네트워크를 표현합니다.

2-4. Example

Network Motif의 유무에 따른 두 가지 경우를 제시합니다. 강의자료에선 Food webs에 대해 설명하고 있습니다.

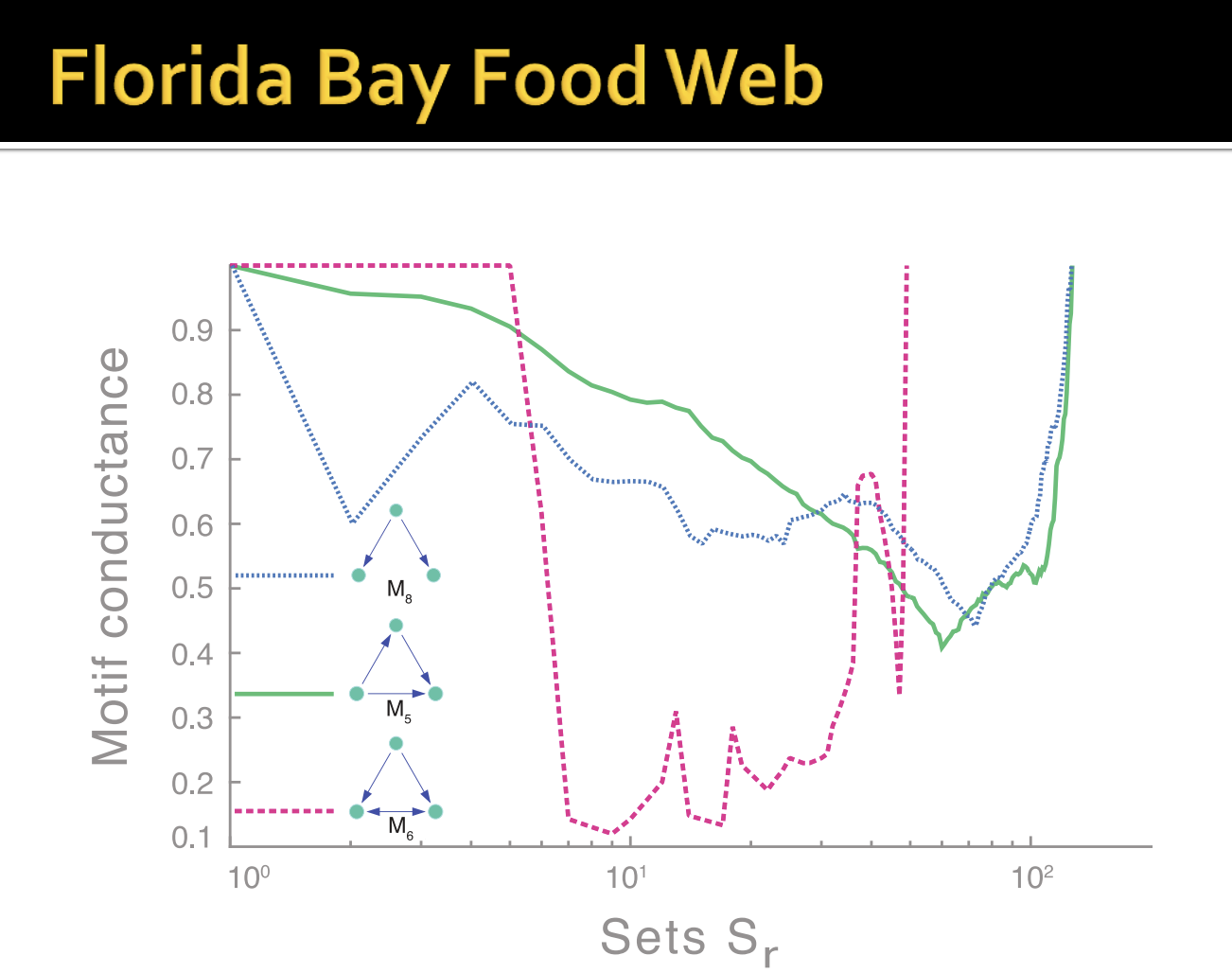
Motif Spectral Clustering을 통해 각 Motif에 따른 결과를 보여줍니다.

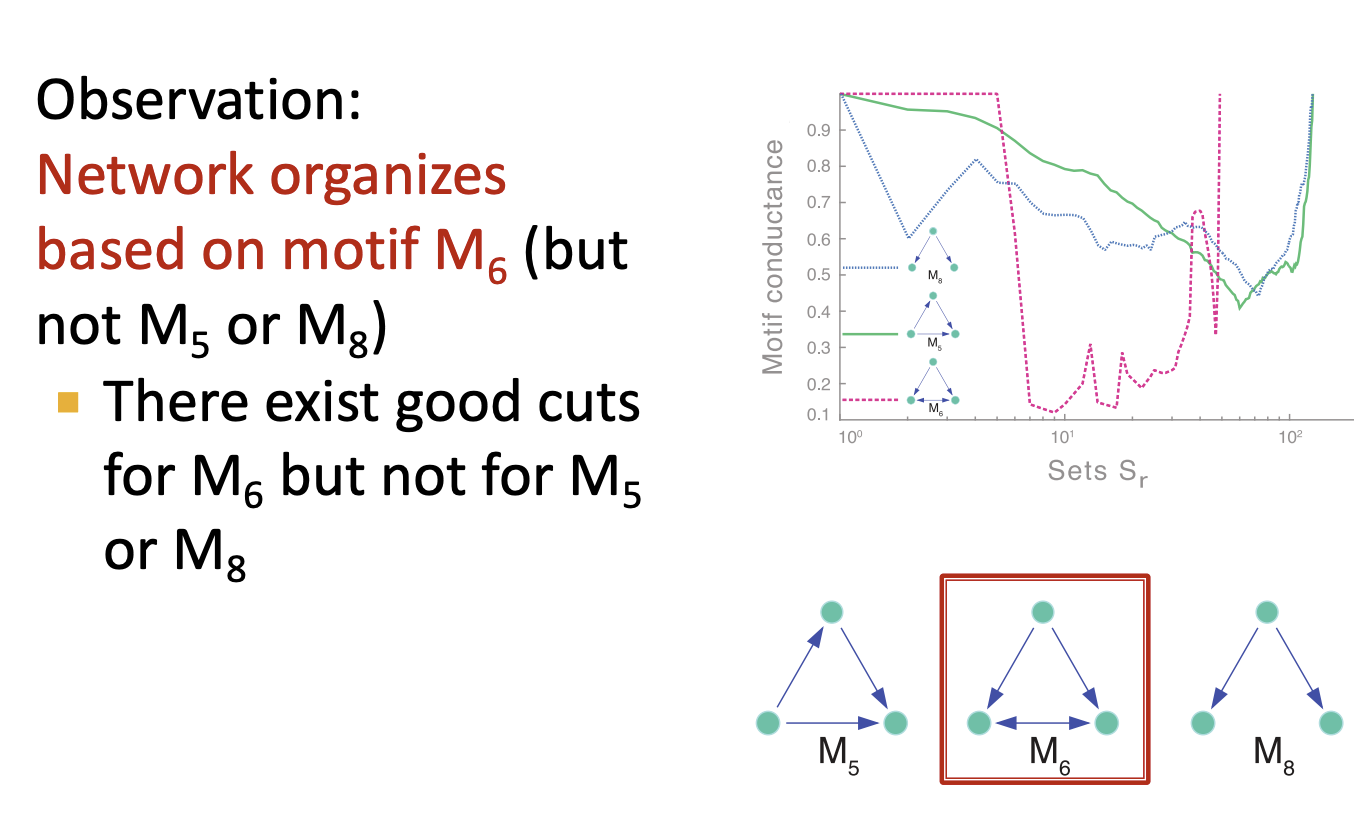
여기서 특정 Motif를 설정하였을때 파티셔닝은 다른 Motif에 대해서는 좋은 파티셔닝이 아니라고 합니다.

tobigsGNN

2021 투빅스 GNN 스터디

이전 포스트

4. Community Structure in Networks

다음 포스트

6. Message Passing and Node Classification

5개의 댓글

Carvin

2021년 3월 5일

Lecture 5 Spectral Clustering에서는 이전 강의에서 다룬 motifs와 community에 대한 개념을 기반으로 graph에 존재하는 community, 군집을 찾는 방법에 대해 소개합니다.

그래프에서 군집, Community 이란 다음 조건을 만족하는 정점의 집합입니다. 모호한 표현이 사용되었기에 수학적으로 약속된 정의라고 할수는 없지만 시각적으로 표현되었을 때, 군집의 의미를 파악할 수 있습니다.

집합에 속하는 정점 사이에는 많은 간선이 존재함
집합에 속하는 정점과 그렇지 않은 정점 사이에는 적은 수의 간선이 존재함

그래프에 존재하는 군집을 구분하는 문제를 군집 탐색, Community Detection 이라고 합니다.

보통은 각 정점이 한 개의 군집에 속하도록 군집을 구분하기 때문에 비지도 기계학습 문제인 클러스터링, Clustering과 상당히 유사하며 graph 기반 군집화 기법은 Spectral Clustering이라고 합니다. 해당 과정은 Graph Partitioning이라고도 부르는 것으로 이해했습니다.

Spectral Clustering에는 3개의 Step이 있습니다.

Preprocessing: 그래프를 matrix representation하는 과정
Decomposition: matrix의 eigenvalue와 eigenvector를 구함으로써 차원축소?하는 과정
Grouping: 공간에 투영된 벡터를 군집화하는 과정

 먼저 ‘good’ partition에 대한 정의가 요구됩니다. 여기서 ‘Minumum-cut’과 ‘Conductance’ 2가지 기준을 제시합니다. Minimum-cut의 경우는 두 그룹간의 연결성이 가장 최소가 되는 부분을 찾는 것으로 이해했는데, 이 방법은 군집 간 연결관계는 고려하나 군집 내 연결관계는 고려하지 못한다는 단점이 있습니다. Conductance는 두 그룹의 density 대비 그룹 간 연결성을 고려하게 됩니다. 모든 노드의 그룹을 고려하며 conductance를 구하는 것이 가장 이상적인 방법이지만 NP-hard 문제로 현실적으로 불가능함을 언급합니다.

다시 Spectral Clustering의 과정에 대해 살펴보면

먼저, Preprocessing에서 matrix representation을 구하는 방법으로 차수행렬(D)에서 인접행렬(A)를 빼주어 얻게되는 Laplacian Matrix를 얻게됩니다. 그 뒤로 Laplacian Matrix와 노드 정보 벡터 행렬를 기준으로 eigenvalue와 eigenvector를 구하게 됩니다. 그리고 최종적으로 eigenvector를 비교함으로써 grouping 해나가는 것으로 이해했습니다.

이제 최적의 군집 개수를 설정하는 것에 있어서는 연속된 두 eigenvalue 간의 차이를 최대화하는 k 군집 개수를 찾는다고 합니다.

한편, 그래프에서 Spectral Clustering하는 방법으로 motif-based 방식이 있다고 말합니다. 해당 방식 또한 3개의 step이 존재합니다.

Preprocessing: 그래프에서 주어진 motif가 적용된 weighted graph를 도출함
Decomposition: weighted graph 기반 laplacian Matrix를 구하고 분해함
Grouping: 똑같은 방식으로 grouping!

답글 달기

2021년 3월 7일

keyword : graph clustering

좋은 partition = 그룹 내 node 간 edge가 최대가 되며 그룹 간 edge가 최소가 되게끔 하는 것입니다.
군집을 나누기 위한 방법에는 여러 가지가 있는데, 1. minimum cut을 고려하면 군집 간의 연결만 고려하기 때문에 좋지 않고, 2. 각 그룹의 Density 대비 그룹간의 connectivity 를 구하는 conductance 값을 고려하게 되면 연산이 커져 힘들어집니다.
따라서 graph matrix 를 통해 계산된 eigenvector, eigenvalue 값을 통해 partitioning 하는 Spectral Clustering 을 배우게 됩니다.

Spectral Clustering

d-regular graph 에서, 고유값 분해를 통해 {x=(1,1,...,1), λ=d} 라는 상응하는 one pair 를 찾을 수 있습니다. partitioning 을 위해 graph가 2개의 d-regular component로 구성되어 있다고 가정했을 때, 두 케이스 모두 $\lambda_n=d$ 라는 eigenvalue 값을 공통으로 가지게 되는 것을 알 수 있습니다. $\lambda_n=d$ 에 대응되는 $x_n=(1,1,...,1)$ 에 대해, 대칭행렬의 eigenvector들은 orthogonal 하므로, $x_n \cdot x_{n-1} = 0$ 이 됨을 알 수 있고, 위의 식을 풀어 보면 $x_{n-1}$ 원소 값들의 합은 0이 됨을 알 수 있습니다. 따라서 두 번째로 큰 eigenvalue 값인 $\lambda_{n-1}$ 값에 대응되는 eigenvector 인 $x_{n-1}$ 에서, 0 값을 기준으로, 대소 여부를 판단해 partitioning을 진행합니다.

Matrix Representations

L = D - A

L : Laplacian Matrix
D : Degree Matrix
A : Adjacency Matrix

Laplacian Matrix 에서는 행/열의 값을 다 더하면 0이 되므로, $x=(1,1,...,1)$ eigenvector 에 대하여 $Lx=0$ 이므로 이에 대응하는 $\lambda_1 = 0$ 이 됩니다. 따라서 Laplacian Matrix 에서는, 2번째로 작은 eigenvector $x_2$ 에서, 0보다 작은 값은 왼쪽으로, 0보다 큰 값은 오른쪽으로 모아서 partitioning을 진행합니다.

Spectral Partitioning Algorithm

Pre-processing : Laplacian Matrix L 생성
Decomposition : Lx=λx, $\lambda_2$ 에 상응하는 $x_2$ 찾기
Grouping : $x_2$ 에 있는 node들에 대해, split 기준을 잡아 clustering

Motif-Based Spectral Clustering

node 기준이 아닌, motif 기준으로 partitioning 을 진행합니다.
위에서 진행한 방법과 동일하게 Spectral Clustering 으로 진행되며, 찾고자 하는 motif subgraph를 찾고 egde 에 가중치를 주는 Matrix W 를 생성해 Partitioning 을 진행합니다.

자세한 건 리뷰에 적었어용 좋은 강의 감사함니다 ~

답글 달기

이예진(지니)

2021년 3월 7일

블로그 리뷰했습니다..
https://jxnjxn.tistory.com/69?category=877774

답글 달기

김태욱

2021년 3월 7일

이번 강의에서는 이전 강의에서 다룬 개념을 기반으로 그래프를 군집화하는 방법에 대해 배웠습니다.

Spectral Clustering Algorithms

Pre-processing: 그래프를 표현하는 matrix 생성
Decomposition: matrix의 eigenvalue와 eigenvector를 계산, eigenvector를 기반으로 low-dimensional representation
Grouping: 새로운 representation을 기반으로 point들을 2개 이상의 cluster에 할당

Partitioning

좋은 파티션이라 함은 그룹내 노드간 간선이 최대며 그룹간의 간선이 최소여야 함.
Modularity와 비슷한 개념이며 강한 연결을 지닌 서브 네트워크를 식별하여 분리.

Edge cut

파티션을 표현하는 목적함수로 그룹에서 종점이 있는 간선 수로 나타낼 수 있음.
두 파티션에 대한 최소 edge cut를 얻는 것이 목표. 하지만 이는 오로지 군집간의 연결만 고려하였고 군집 내부의 연결성에 대해선 전혀 고려하지 않았음

Conductance

군집간 연결성을 비교하는데 각 군집의 밀도를 반영하며 edge cut값이 작고 min(vol(A), vol(B))의 값이 커진다면(=두 군집의 밀도가 유사) 작은 Conductance값을 얻을 수 있음
좋은 파티션을 알아내기 위해선 최소 Conductance값을 구해야 하는데 이는 NP-hard 문제로 인해 쉽지 않음
NP-hard: 대표적으로 TSP(Traveling Salesman Problem)문제가 있는데, 그래프내 간선을 전부 비교하면서 문제를 해결하는 방법으론 다항시간내에 풀 수 없음. 이러한 NP-hard문제를 해결하기 위해서 휴리스틱한 방법이나 가지치기, 탐욕법등의 방법을 적용

Spectral Graph Partitioning

그래프 G의 모든 노드들이 차수 d를 가지는 d-Regular Graph가 있을 때, 가장 큰 eigenvalue는 d.
eigenvector들은 직교(orthogonal)함으로 서로 곱하였을때 0이 나와야하며, 다른 eigenvector 값들의 합은 0이 되어야 함.
이를 통해 두 그룹의 노드 정보에 대해 양수, 음수 그룹으로 나누어 표현.

Spectral Partitioning Algorithm Summary

Partition을 찾는 좋은 방법은 그래프에서 얻은 행렬에서 eigenvalue, eigenvector를 사용하여 추정하는 것.
1) Pre-processing: 그래프의 인접행렬과 차수행렬을 통해 Laplacian 행렬을 얻습니다.
2) Decomposition: Laplacian 행렬의 eigenvalue, eigenvector 구해주며, 집중해야할 값은 람다2 입니다.
3) Grouping: 이전 단계에서 얻은 eigenvector애 담긴 노드 정보로 Grouping을 하여 Partitioning을 진행. 나이브하게 접근하면 0 또는 중간값으로 분리하여 파티셔닝을 하고 벡터내 값을 정규화하여 노드의 파티션을 정합니다.

Motif-Based Spectral Clustering은 위와 다르게 노드가 아니라 motif를 기준으로 partitioning을 진행합니다.

좋은 강의 감사합니다!

답글 달기

제갈식

2023년 10월 31일

영상처리를 통해 눈으로 쉽게 배우는 푸리에 변환 입니다.
https://www.aladin.co.kr/shop/wproduct.aspx?ItemId=309060931

강력 추천합니다.

답글 달기