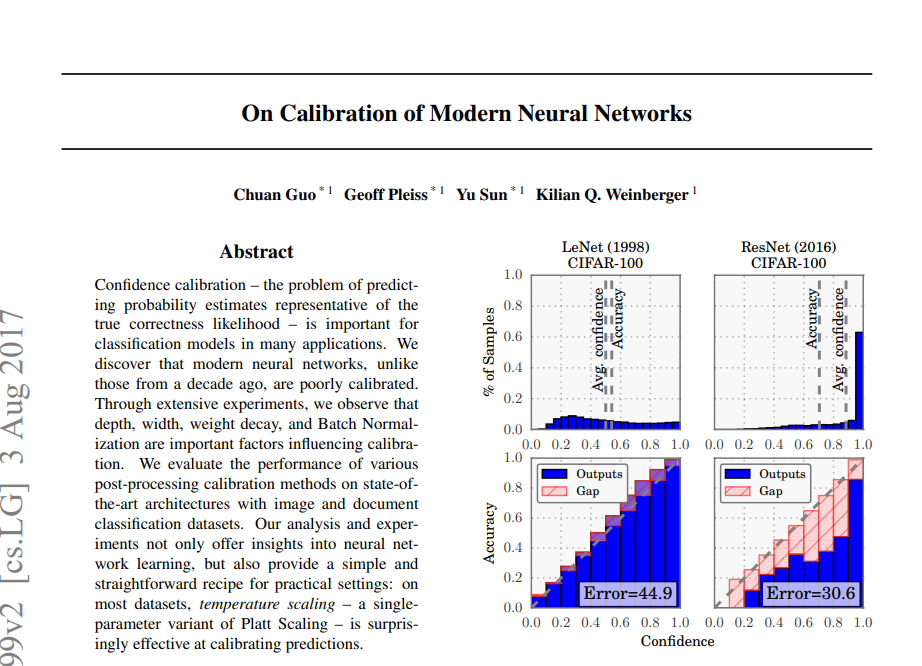
딥러닝 모델을 평가할 때 흔히 정확도만을 평가합니다.
하지만 정확도가 높다고 실제 산업에서 사용할 수 있을까요??

당연히 아닙니다. 이에 대한 답을 이번 글에서 다뤄볼 예정입니다. 이번에 참고한 자료는 고려대학교 DMQA의 "On Calibration of Deep Neural Networks" 세미나 영상(배진수)입니다. 생소할 개념일텐데, 이번 글을 통해 알아두시면 좋을 것 같습니다.

출처: http://dmqa.korea.ac.kr/activity/seminar/407

[Calibration]

딥러닝이 발전하면서 우수한 성능을 가지게 되었습니다. 하지만 아무리 높은 정확도를 가졌다고 하더라도 오작동 기회비용이 큰 분야(ex. 자율주행, 의료)에서 바로 사용할 수는 없습니다.

자료의 설명을 가지고 오면,

만약 정확도가 95%로 같은 모델 1, 2가 있을 때 실제 환자는 질병 B를 가지고 있으나, 두 모델 전부 정상으로 예측했다고 생각해봅시다.

두 모델 전부 틀린 예측을 했지만 모델 1, 2 중 모델 2가 불확실한 상태로 틀렸기 때문에 모델 1보다 더 신뢰할 수 있는 모델이라고 할 수 있습니다.

그리고 이처럼 신뢰할 수 있냐, 없냐를 평가하는 지표를 Calibration이라고 합니다.

[신뢰할 수 있는 모델의 특성]

"신뢰"의 개념을 이해하기 위해 신뢰할 수 있는 모델의 특성에 대해 다뤄보겠습니다.

이미지 분류 모델은 위와 같이 정확도가 80%인 모델 1, 2가 있다고 할 때 모델 1에서는 왼쪽 고양이 사진을 고양이라고 예측할 확률을 78%라고 합니다. 반면, 모델 2에서는 고양이라고 예측할 확률을 98%라고 합니다. (이해가 되지 않는다면 MLP 모델에 대해서 곧 게시글을 올릴 예정이니 참고하시면 좋을 것 같습니다.)

이와 같은 상황에서 만약 다음처럼 모델 1, 2가 있다고 할 때

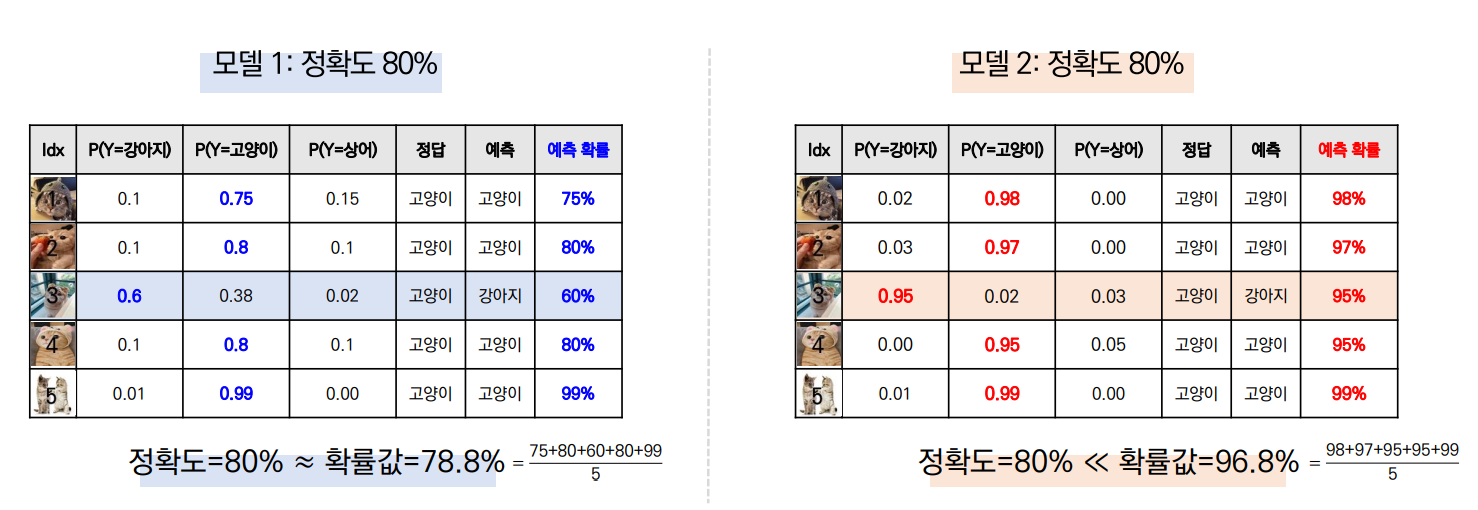
모델 1부터 살펴보면, 첫번째 행에서 정답이 고양이일 때 정답인 고양이로 예측할 확률이 75%, 세번째 행에서는 정답이 고양이일 때 강아지로 틀린 예측을 할 확률이 60%입니다.

반면 모델 2에서 첫번째 행은 98%로 옳은 예측을 하고, 세번째 행에선 95%로 틀린 예측을 합니다.

이때 각 예측 확률의 평균을 냈을 때 모델 1은 전체적으로 정확도와 유사하지만 모델 2의 경우는 정확도에 비해 예측확률이 매우 높은 것을 알 수 있습니다.

이러한 상황에서 무슨 모델이 더 신뢰할 수 있는 모델일까요?

바로 모델 1입니다.
왜냐하면, 모델 2는 정확도에 비해 Overconfident한 예측을 하기 때문이죠. 너무 과신한다는 의미입니다. 따라서 우리는 예측 모델의 확률 결과와 정확도가 유사한 모델을 더욱 신뢰할 수 있습니다.

또한, Calibration을 수식적인 방법을 통해 평가할 수도 있습니다.

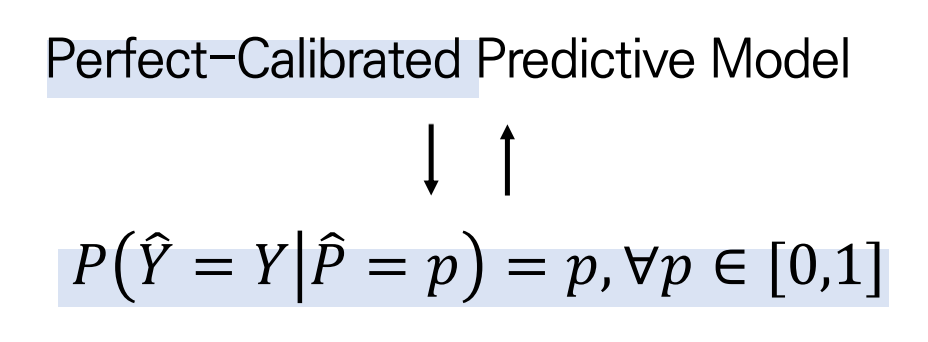
자료에 따르면, Perfect Calibration한 모델은 예측 확률이 $p$라고 주어졌을 때, 예측한 결과 $Y$가 실제 정답인 $\hat{Y}$일 확률이 예측 확률 $p$와 같은 모델을 의미합니다.

즉, 좌변 $P(\hat{Y} = Y |\hat{P} = p)$은 모델의 정확도를, 우항 $p$는 예측 확률을 의미하고 모델의 정확도와 예측확률이 같을 때 그 모델을 Perfect Calibration하다는 말입니다.

따라서 $p$가 0과 1 사이의 값을 가질 때, $|P(\hat{Y} = Y |\hat{P} = p) - p|$가 작을수록 Perfect Calibration에 가까워집니다.

그리고 모델의 Calibration을 평가하기 위해 계산 가능한 수치로 나타내고자 다음과 같은 식을 사용하여 계산한다. 이때 우변을 Calibration의 평가지표인 Expectation Calibration of Error(ECE)라 한다.

여기서, $M$은 데이터 내에 집단 개수, $n$은 전체 데이터의 개수, $|B_m|$은 집단 $B_m$의 데이터의 개수, $acc(B_m)$은 집단 $B_m$에 대한 예측 모델의 정확도, $conf(B_m)$은 집단 $B_m$에 대한 예측 모델의 확률값들의 평균을 의미한다.

[ECE의 시각화]

Calibration을 시각화하기 위해선 두 가지 방법을 사용한다.

1. Confidence Histogram

첫번째 방법은 $M$=1로 두고, $|acc(D)-conf(D)|$을 계산하는 confidence histogram이다.

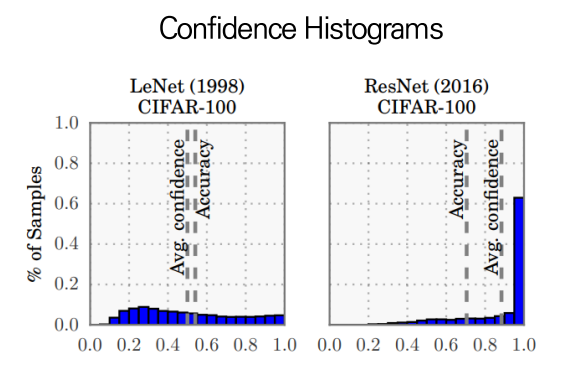
위 자료를 살펴보면 왼쪽은 1998년도에 나온 LeNet라는 모델이고, 오른쪽은 2016년도에 발표된 ResNet이라는 딥러닝 모델이다.

왼쪽 모델의 경우 오른쪽 모델에 비해 Accuracy가 낮지만, Accuracy와 평균 Confidence가 비슷하다. 반면 오른쪽 모델은 Accuracy가 왼쪽 모델에 비해 높긴하지만 Accuracy에 비해 평균 Confidence가 높아 overconfidence함을 보인다.

2. Reliability Diagrams

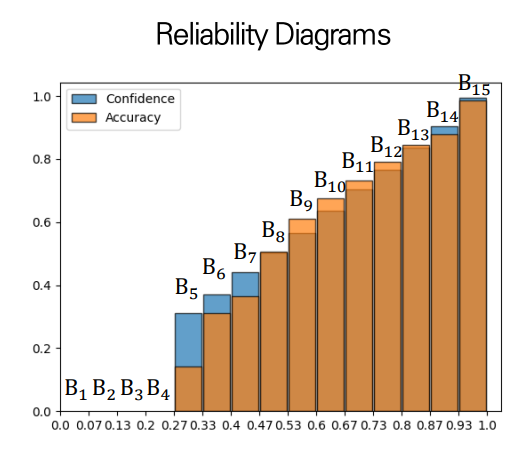
다른 Confidence 시각화 방법은 reliability diagram이다.

전체 데이터를 $M$개의 데이터셋으로 나누고, 각 구간마다의 정확도와 confidence를 계산하여 표시하여 나타낸 diagram이다. 이때 정확도는 예측값이 얼마나 실제값과 일치했는지, 신뢰도는 모델의 예측값의 평균으로 계산한다.

[Testing]

따라서, Calibration은 Testing data에 대한 ECE 지표, Reliability Diagrams, Confidence Histogram를 확인해야하고, Noise(corrupted) Testing data에서도 ECE 지표, Reliability Diagrams, Confidence Histogram를 확인하여 더 정확하게 모델의 Calibration을 확인할 수 있다.

[Calibration of (Modern) Deep Neural Networks]

Calibration의 의미와 평가 방법에 대해 다뤘으니, 이번 단원에선 요즘 사용하는 딥러닝 모델의 calibration을 살펴보겠습니다.

자료에 따르면, 현대에서 사용하고 있는 딥러닝 모델들의 공통점은 "크고 넓고 무겁고 높은 정확도를 가진다"는 것이다. 크고 넓고 무거운 모델은 학습 데이터의 개수가 적더라도 일반화 성능이 뛰어나기 때문에 더 정확도를 가지기 때문이다.

하지만 이와 반대로 신뢰도는 떨어지고 있다. 특히 신뢰도는 Depth와 합성곱 연산 필터의 개수, Batch Normalization, Weight Decay와 다음과 같이 연관되어 있다.

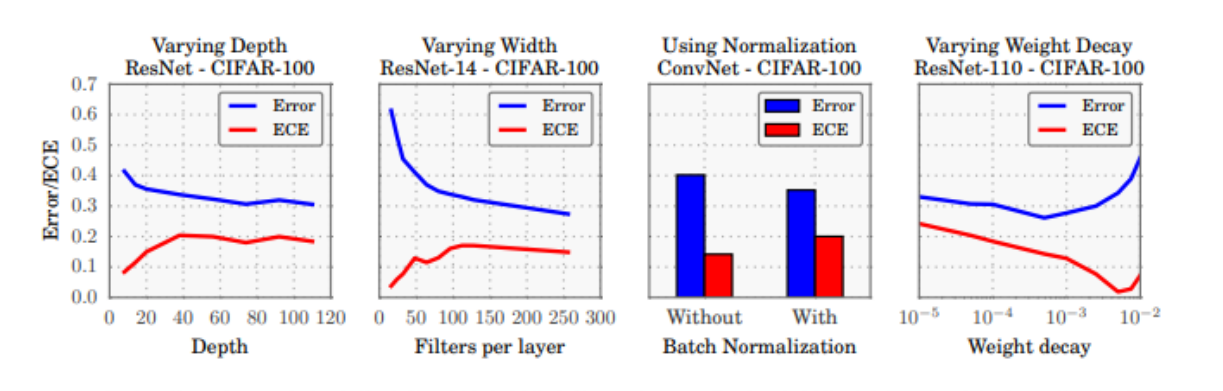
Depth가 깊어질수록, 합성곱 연산 필터는 많아질수록 Error가 줄어들어 정확도가 높아지는 반면, ECE는 높아지기 때문에 Calibration 지표는 나빠지고 있습니다. 또한, 배치정규화를 해도 Error는 낮아지는 반면 ECE는 높아지며 L2 규제의 가중치가 줄어들 때도 ECE와 Error가 반비례하는 경향이 있습니다.

다음으로 만약 학습 데이터에 대한 정확도가 100%라도 Cross-Entropy 기준 학습이 계속해서 이뤄진다면 loss function에 맞게 계속 학습되어 Overconfidence가 발생하게 됩니다.

그럼 어떤 구조를 가진 이미지 분류 모델이 더 좋은 신뢰도를 가질까요?

2021년 연구에 따르면 Convolutional model과 non-convolutional model 중 non-convolutional model이 신뢰도와 정확도 모두 높다고하며사전학습을 하는 모델의 경우 정확도는 향상되지만 신뢰도 성능은 변함이 없었습니다.

따라서, 다음과 같이 정리됩니다.

• Convolutional model: 모델 사이즈가 커질수록 정확도 성능은 향상되지만 신뢰도 성능은 떨어지는 추세
• Non-Convolutional model: 신뢰도 성능이 전반적으로 좋은 편이며 다량의 데이터 기반 사전학습 시 정확도까지 우수함

또한, Noise Data에 대해서는 두 유형의 모델 전부 정확도와 신뢰도가 양의 상관관계를 가지며 Non-Convolutional model의 성능이 전반적으로 노이즈 강도에 대해 Robust하다는 결과가 나타났습니다.

[Improving Calibration of Deep Neural Networks]

그러면 딥러닝 모델의 Calibration을 향상시키기 위해선, Overconfidence를 해결하기 위해선 어떤 방법을 사용할 수 있을까.

1. Label Smoothing

첫번째 방법은 Label에 Smoothing을 적용하는 것입니다.

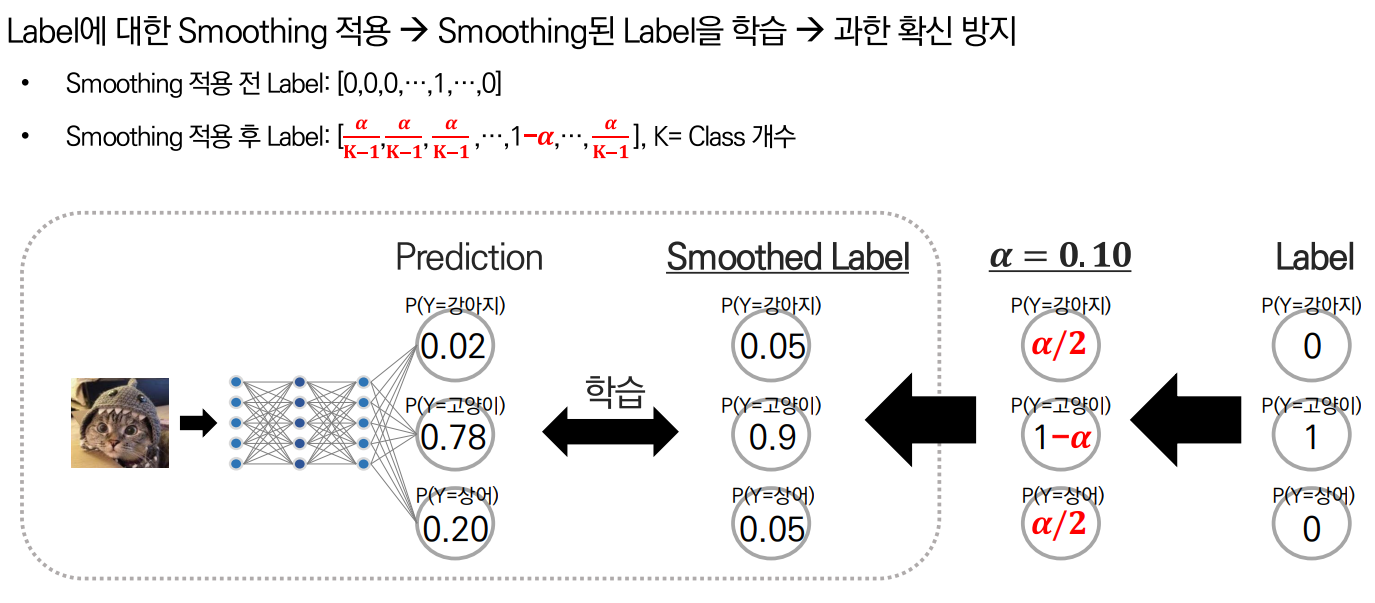
0과 1로 기존 Label이 구성되지만 Smoothing을 통해서 1의 값을 $1-\alpha$를, 0의 값은 $\frac{\alpha}{K-1}$로 대체하여 Cross-Entropy 계산 시 Overconfidence를 방지하는 역할을 합니다.

2. 엔트로피 정규화

두번째 방법은 과하게 확신하는 예측 사례에 대해 패널티를 부여(=엔트로피 정규화)하는 방법입니다.

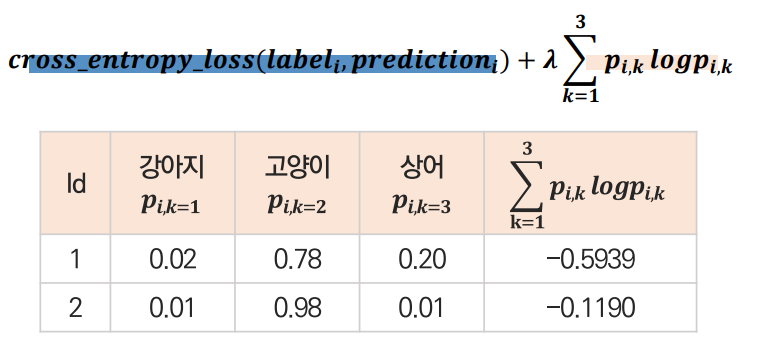
이는 1번 방법처럼 Label을 보정하는 것이 아닌 이번엔 prediction을 보정하여 해결하는 방법입니다. 일반적인 규제화 방법처럼 Cross entropy Loss function에 Negative Entropy Loss Term을 추가해서 패널티를 부과하는 방법입니다.

위 방법을 통해 Id 2보단 Id 1의 결과가 나오도록 조정해주는 것입니다. Id 2처럼 Overconfidence가 발생할 확률 패널티 값을 작게 빼주어 Loss function이 크게 줄어들지 못하는 반면 Id 1은 확률패널티 값을 크게 빼주어 확신하지 못할 때 더 loss function을 작게 만들어줌으로써 규제화하는 방식입니다.

3. Mix-up 증강기법

마지막으로 Mix-up 증강기법 적용을 통해 Over confidence를 방지하는 방법입니다.

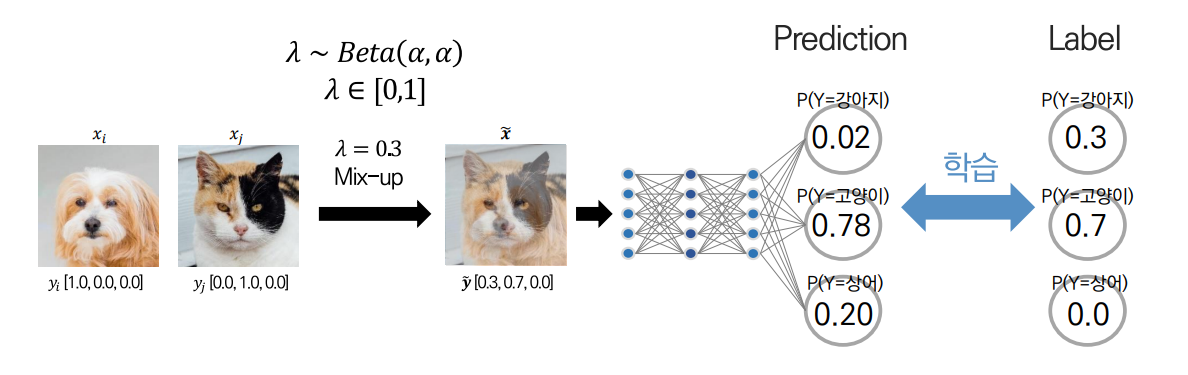
이는 0과 1로만 구성되어 있는 One-Hot Encoding Label을 학습하는 대신 0과 1 사이로 Convex Combination된 Label을 학습하여 개선하는 방식입니다.

이를 통해 One-Hot Encoding Label을 학습한 것이 Overconfidence의 주된 문제점임을 의미한다는 것을 파악할 수 있습니다.

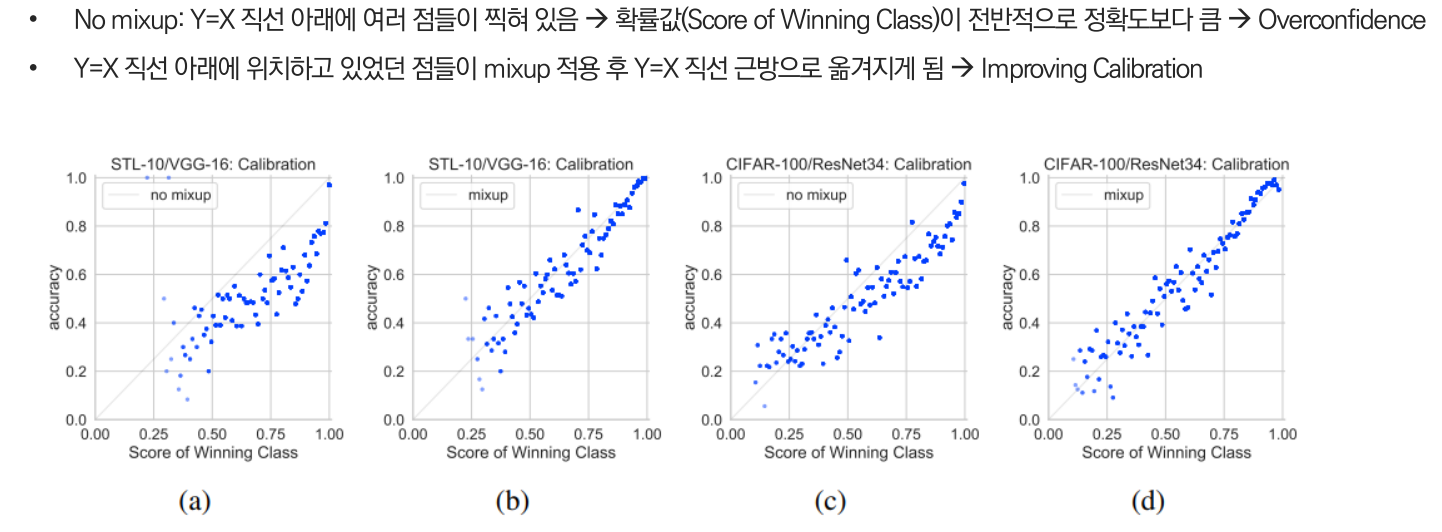
자료를 보면, No mixup인 경우 전체적으로 Y=X 직선 아래에 여러 점들이 찍혀있어 OverConfident한 반면 Mixup을 하게 되면 Y=X 직선 근방으로 옮겨져 Calibration을 개선한 것을 확인할 수 있습니다.

[지표 제안]

자료에서 참고한 논문에 따르면 기존의 ECE 지표가 아닌 Overconfidence Error를 제안합니다.

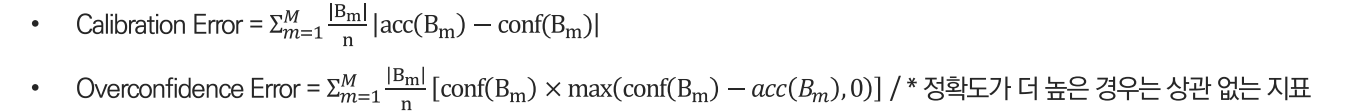
Overconfidence Error를 평가지표로 사용하면 Calibration보다 OverConfidence에 대해 더욱 명확하게 평가할 수 있습니다.

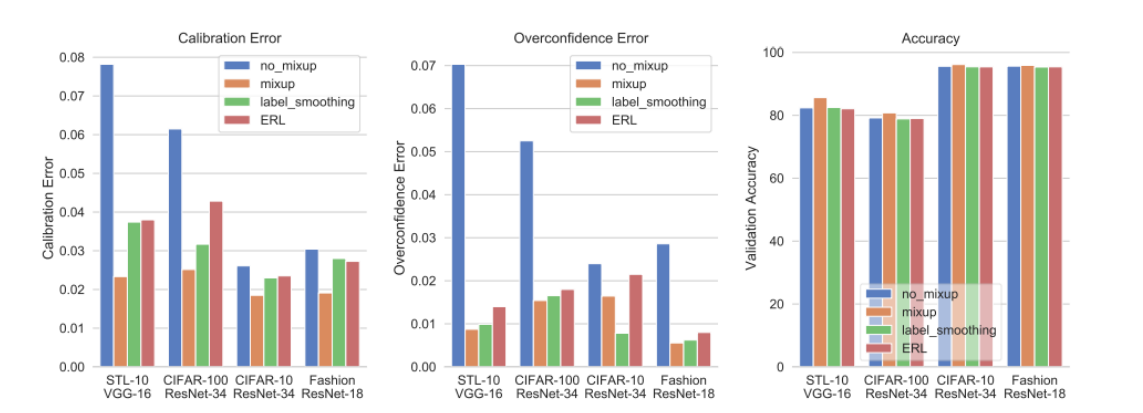
위 결과를 보면 Accuracy에서는 Mixup을 하게 되면 성능이 더욱 좋아지며, Calibration Error 역시 가장 낮은 것을 보인다. Overconfidence Error에서도 mixup이 일반적으로 더 좋은 성능을 보이는 것을 확인할 수 있습니다.

[Conclusion]

정리하자면, Calibration은 모델이 갖고 있는 특성 중 하나로, 모델이 출력한 결과와 실제 정확도가 얼마나 비슷한지를 나타내는 지표입니다.

예측 정확도(Accuracy)는 물론 신뢰도(Confidence)가 모두 우수해야 실제 산업에서 믿고 사용할 수 있습니다.

다음으로 Convolutional Neural Networks는 정확도는 개선되고 있지만 Calibratoin은 떨어지고 있는 추세로 Non-Convolutional Neural Networks는 정확도와 Calibration이 모두 우수하나, 대규모 사전학습을 필요로 한다는 것을 알 수 있었습니다. (특히, Self-Attention, Perceptron 연산을 사용하는 모델이 Well-Calibrated 되는 경향이 있습니다.)

개인적으로, 느낀 바를 말하자면 자율주행과 의료 분야와 같이 기회비용이 큰 분야에서 분류 문제를 해결해야 하는 경우 해당 지표인 Calibration을 고려한다면 실제 산업에서 적용할 수 있는 모델을 만드는 데 확실히 도움이 될 것 같습니다.

또한 일반적으로 더미 변수 등등에서 0과 1로 구성하여 모델을 만드는 경우가 많은데 이 경우 Loss function에서 이를 사용한다면 좋지 않은 결과가 나올 수 있다는 것을 생각해보게 되는 계기가 된 것 같습니다. 이번 글을 통해 모델을 모델링할 때 평가지표 내지 Loss function을 해결하고자 하는 문제에 맞게 적절하게 선정해야함을 다시 생각해보면 좋을 것 같습니다.