이번 글은 논문이 게재되었을 당시 SOTA에서 많은 조회수를 기록하고 뛰어난 성능을 가진 것으로 유명했던 시계열 예측 모델인 SCINet을 가지고 왔습니다.

최근 시계열분석에 대해 관심을 많이 가지고 있는데, SCINet이라는 모델이 워낙 유명하고 Dacon 공모전에서 우수한 성적을 거둔 분들이 활용했던 모델이고 코드도 잘 나와있어서 한번 공부해보고 싶은 마음에 가지고 오게 되었습니다.

개인적으로는 SCINet을 통해 처음 최신 AI 논문을 접하게 되어 제게 의미가 큰 논문입니다. 그때 당시엔 지금보다 공부가 미흡하여 제대로 공부하지 못했는데, 지금도 완벽히 이해하기엔 부족하겠지만 다시 한번 복습해보고 싶어서 가지고 오게 되었습니다.

자료는 서울대학교 산업공학과 DSBA 연구실 소속 이정호 님의 유튜브 영상을 참고하였으며 링크는 아래와 같습니다.
DSBA SCINet 논문 리뷰 영상

또한 본 논문은 SOTA에서도 Star가 엄청난 논문이고 코드도 잘 구현되어 있습니다. 본 연구에 대한 논문과 깃허브 링크는 아래 링크를 통해서 확인할 수 있습니다.
SCINet 논문 & 깃허브

[Introduction]

[시계열 데이터의 특징]

시계열 데이터는 Cyclical, Trend, Seasonal한 특징을 가지고 있으며 그 과정에서 Irregular fluctuation(불규칙한 파동)이 있다. 그래서 시계열 모델은 이러한 특징이 고려되어야 하지만 대개 모델들은 이를 잘 고려하지 않는다.

이에 대해 SCINet의 저자들은 부분적으로 Sampling을 취해서 Sequence를 만들었을 때 부분적인 sequence를 뽑더라도 전체적인 Cyclical, Trend, Seasonal한 특징은 보존되어야 한다고 생각했다.

따라서 저자들은 부분적으로 뽑아낸 Subsequence에 대해 학습을 진행하기로 했다.

Subsequence를 반복적으로 정보를 뽑더라도 Subsequence는 시계열에 대한 특징을 가지고 있을 것이고, 반복적으로 뽑는다면 다양한 Cyclical, Trend, Seasonal한 특징을 뽑아낼 수 있을 것이라고 생각하였다. 이를 통해 Subsequence 사이의 관계를 학습하고자 했다.

[기존의 시계열 딥러닝 모델]

(1) RNN Model: 잘못된 예측이 중첩되어 Long-term에 대해 매우 취약함

(2) Transformer: 모든 시점에 대한 상관성을 학습 $\to$ Long Sequence를 다루기에 비용($O(m^2)$)이 매우 큼

(3) TCN: Long Sequence를 효율적으로 다루지만 Look back (반복되는 정보의 활용)이 부족함
$\to$ 위 그림을 보면 TCN은 Input에서 Conv.Layer 1로, Conv.Layer2, Output과 같이 반복되며 Look back이 되는데, 따라서 TCN 모델은 Conv.Layer의 수만큼만 Look back이 된다는 한계를 가지고 있다.

또한, TCN 모델에서 다뤄지는 부분 중 앞 부분은 많이 다뤄지지도 않는다는 한계 역시 존재

[시계열 예측 Setting]

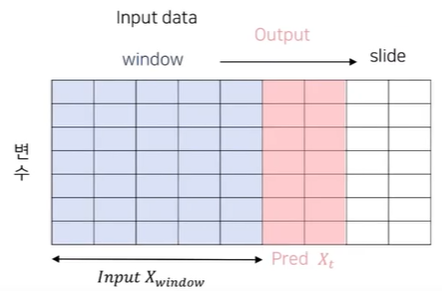
Time Series Forecasting Setting에 대해 먼저 설명을 드리면, Input이 Input window로 들어가고 이 데이터로 next steps에 따라 Pred를 제공한다.

이때 Step의 수에 따라 multi-step forecasting으로 정의한다.

[SCINet]

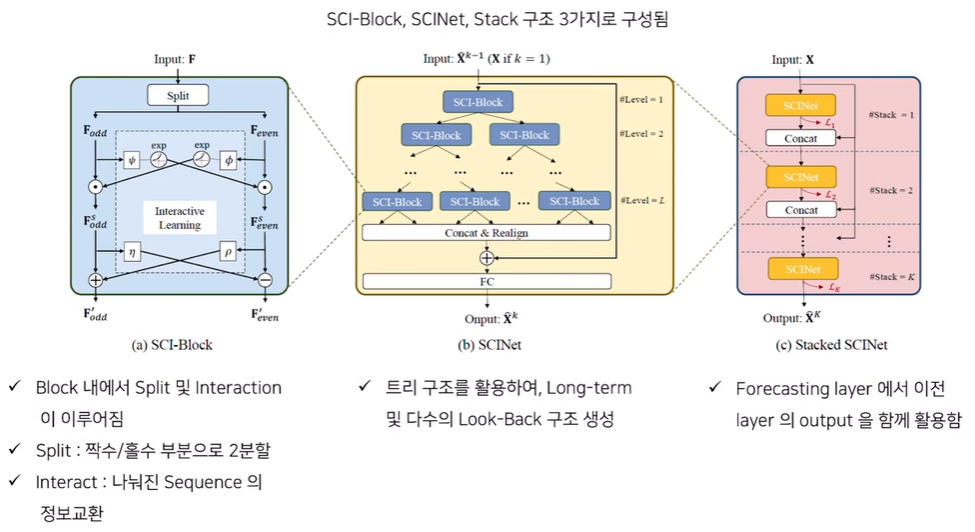
SCINet은 크게 3가지 구조로 구성되어 있는데, Stacked 상태로 SCINet이 있으며 각 SCINet에선 SCI-Block들이 Tree 모형으로 구성되어 있다. 또한 각 SCI-Block은 Split과 Interactive Learning이라는 특징을 가지고 있다.

SCI-Block부터 상세하게 설명을 드리면, Input에 대해 Split을 통해 짝수, 홀수로 분할하고 Interact를 통해 나눠진 Sequence의 정보 교환이 이뤄집니다. 이를 통해 얻어지는 $F'_{odd}, F'_{even}$이 나오고 이렇게 분할되는 과정을 트리 모양으로 쌓은 게 SCINet, 이를 Stacking 한게 모델의 구조이다.
(* 논문에서는 일반적으로 Stack을 1, 2개 쌓아서 활용했다고 언급)

[SCINet-Block]

SCINet-Block을 직관적인 예시로 다시 보여드리자면 다음과 같이 나타낼 수 있습니다.

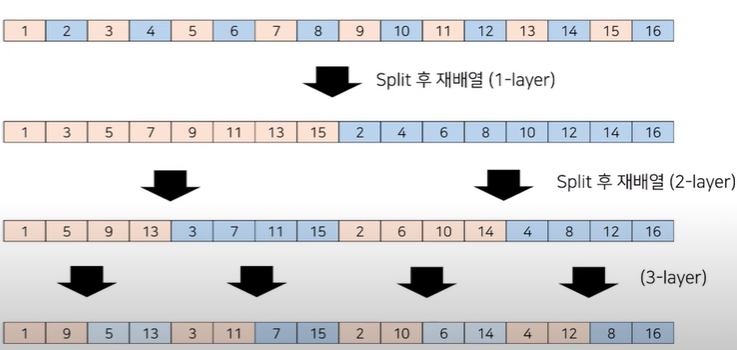
이에 대해 설명하자면,

1, 2, 3, 4, ......, 16으로 구성된 Sequence가 있었다면 홀,짝으로 나눠서 Split을 한 후 재배열 한다. 이후 2-level(그림의 2-layer은 오타)에서 다시 Split하고 재배열 하는 등 이 과정을 각 level에서 반복한다.

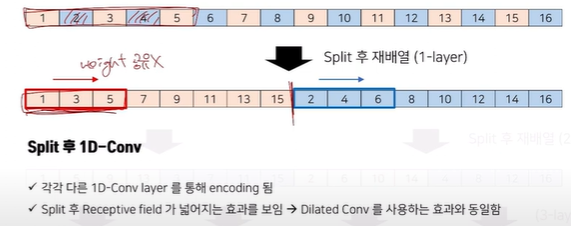
기존 커널이 3인 1D-conv가 있다고 할 때 1, 2, 3까지의 영역을 활용하므로 Long-term을 잡아내는데에 한계가 있었다. 이에 SCINet은 2, 4를 제외하고 홀수인 1, 3, 5만 가지고 Split한 후 1D-conv를 함으로써 Dilated Conv를 활용하는 효과와 동일하게 Receptive field가 넓어져 똑같이 커널이 3인 1D-Conv를 활용하더라도 Long-term 학습에 뛰어난 효과를 보임을 알 수 있다.

이때 각 1D-Conv가 파라미터를 공유하지 않는 이유는 1, 3, 5와 2, 4, 6을 구성하는 각 Down Sample들이 Trend, Seasonality와 같은 정보를 각각 내포하고 있을 것이고 이에 대한 Interaction을 고려해준다면 더욱 많은 Representation을 만들 수 있을 것이라고 생각했기 때문이다.

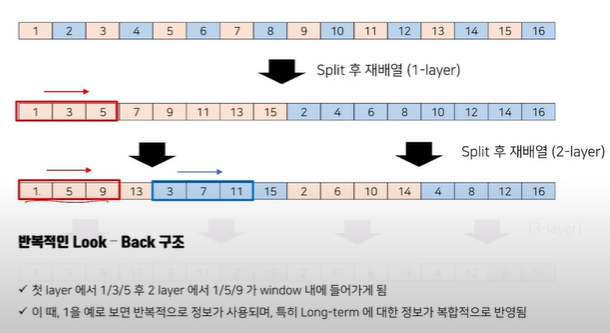
이를 각 Level에서 반복적인 Look-Back 구조를 가져준다면 Long-Term에 대한 정보를 한번에 학습할 수 있다. 또한 커널 사이즈가 고정된 상태에서도 Split을 통해 Long-Term에 대한 정보를 그대로 가져올 수 있다는 큰 특징도 가지고 있다.

그럼 이제 Split을 왜 하는지에 대한 의문이 풀렸다면 이번엔 Interaction하는 이유에 대해 알아봅시다.

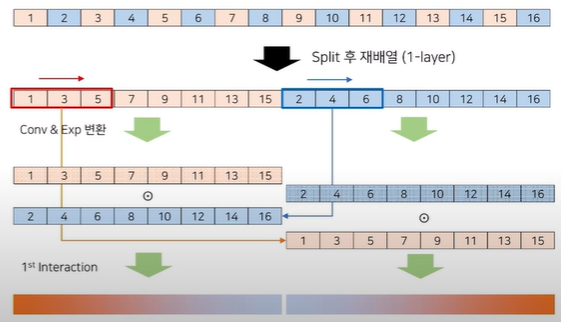
Interaction이 일어난다고 할 때 빨간색 1D-Conv로 구한 값을 지수 변환 해주고, 파란색 1D-conv도 EXP변환을 해준 후 각 값을 곱연산함으로써 1st Interaction을 구해줍니다.

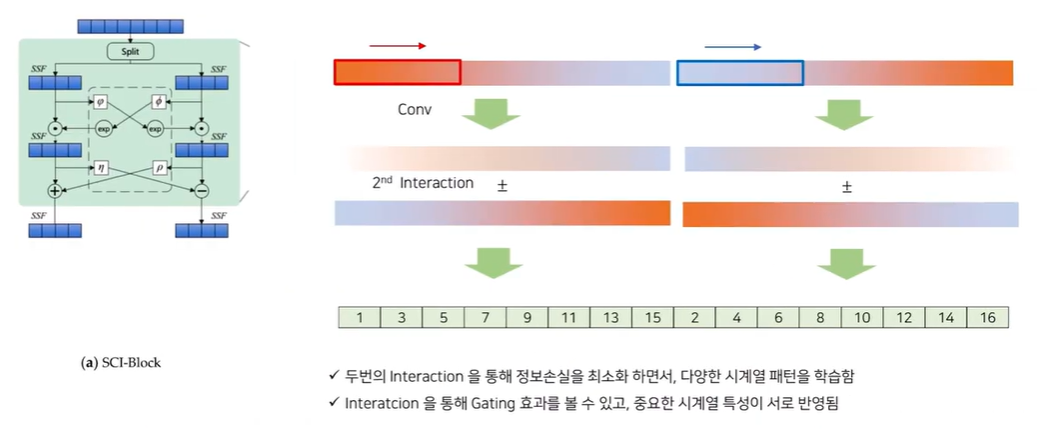
이렇게 나온 Gradation 값을 똑같이 Conv을 통해 Representation을 변환하여 2nd Interaction을 구해줍니다. 이후 앞서 나왔던 1st Interaction과 2nd Interaction을 합차연산(논문의 코드에선 (+)를 사용)을 통해 두개의 연산 값을 이용하여 최종적으로 representation을 만들어줍니다.

[SCINet-Tree]

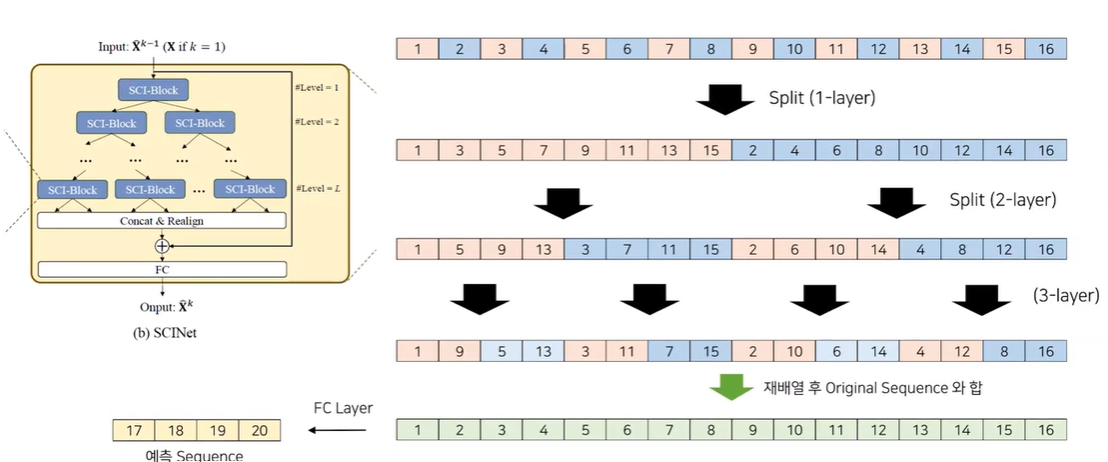
위와 같은 과정을 통해 구해진 최종적인 Sequence를 모두 Concat한 후 재배열 후 Original Sequence와 더하는 연산을 해줍니다. 추가적으로 Fully Connect Layer를 이용해서 차원을 맞춰서 예측 Sequence를 구해줍니다.

[SCINet-Stack]

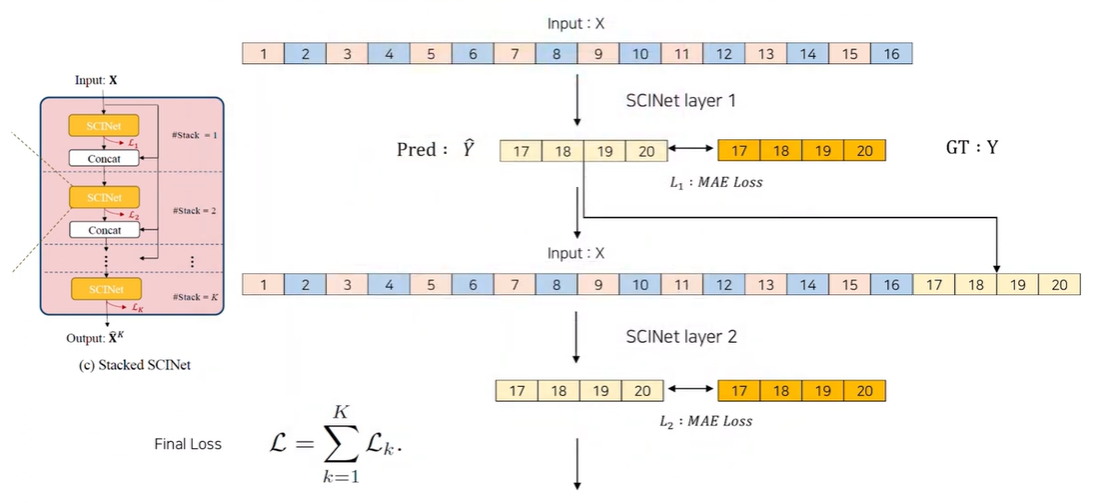
Tree를 통해 얻은 Pred 값을 실제 정답인 17~20의 Sequence와 MAE Loss를 활용하여 Loss를 구해줍니다. 이후 다시 한번 이런 식으로 Stack의 2번째에서 처음 예측한 Pred 값을 합쳐 1~20 Sequence를 모두 활용하여 SCINet의 과정을 반복하며 이 과정 반복은 Stack의 수만큼 진행되게 됩니다.

이를 통해 최종적인 예측결과를 산출하게 됩니다.

[Experiment]

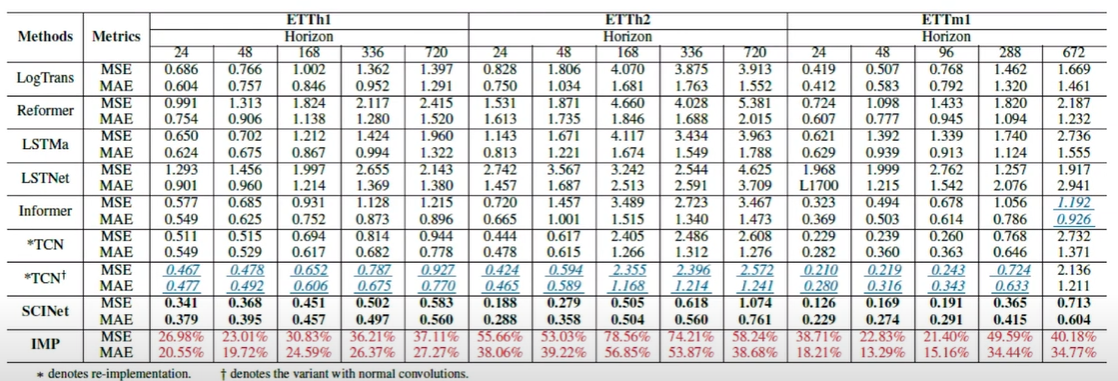
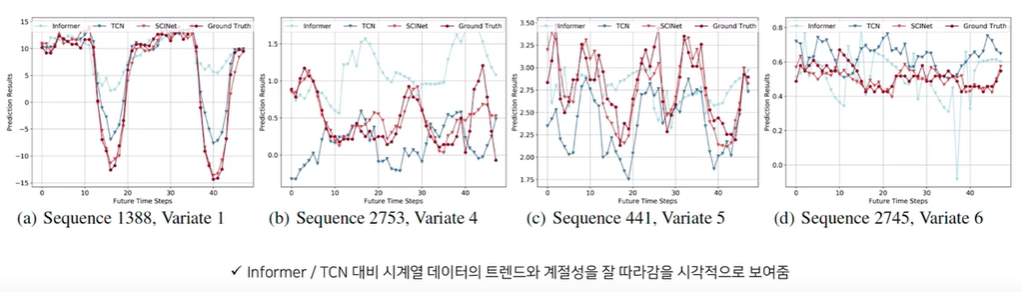
다변수 시계열 예측 데이터셋에서 성능을 살펴보면, Horizon(시계열 예측 기간) 길이가 720과 같이 길어지게 되면 RNN, LSTM 기반 모델의 성능이 매우 떨어짐을 알 수 있다. TCN 모델은 Long-Term forecasting에서 좋은 성능을 가지고 있으나, SCINet의 성능이 더 우수함을 알 수 있다.

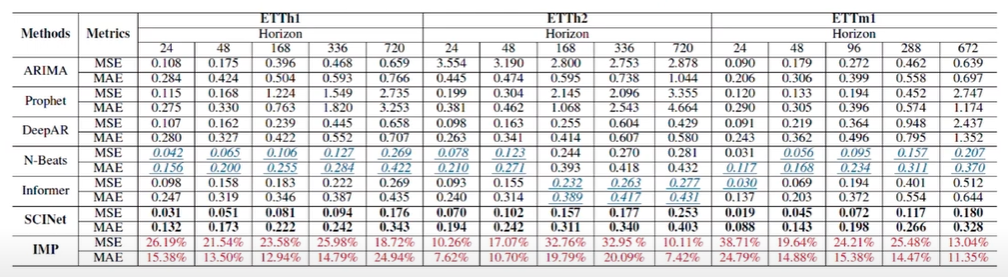
Univariate 데이터셋으로 해당 방법론들과도 비교해보면, 이런 방법들은 Seasonality나 Trend를 활용하는데 SCINet은 이러한 정보를 직접적으로 활용하진 않지만 SCINet이 해당 방법론보다 더 우수함을 알 수 있다.

이는 결국 Split을 해도 Seasonality나 Trend 특성이 보존될거고 그러한 정보에서 뽑아냈으니 그 과정에서 이러한 시계열적인 특성을 가진 것으로 파악됩니다.

[Ablation Study]

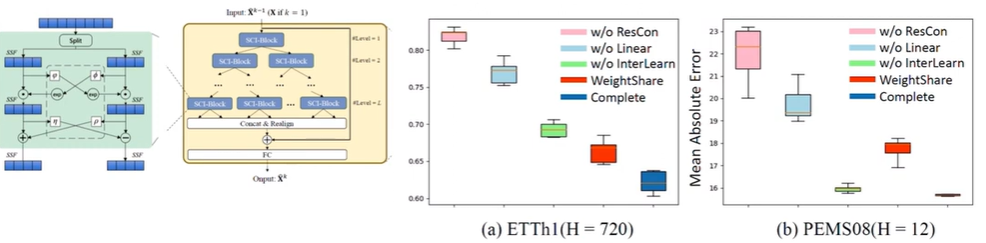
MAE loss 기준으로 Interaction이나 가중치 공유를 해버리게 되면 오차가 급격하게 증가합니다. 또한 마지막에 기존 시계열 데이터를 더해주는 ResCon을 안했을 때도 오차가 급격히 증가했음을 알 수 있습니다.

이때 저자들은 ResCon을 해야하는 이유에 대해 Original data에서도 정보가 있을텐데 Split한 데이터만 사용하게 되면 그 과정에서 Bias가 많이 발생할 수 있다고 생각한다고 합니다.

[Conclusion]

일반적인 시계열 데이터를 수집하고 시간 순서로 정리가 된 데이터에 대해 SCINet을 제한적인 사용을 했을 때 성능이 좋았습니다.

즉, 어느정도 실제 시계열적 특징(계절성, 트렌드 등)이 반영되는 데이터셋에서 좋았지만 불규칙한 시계열 데이터(ex. 이상치)에 대해서는 성능 보장이 힘들다는 것입니다. 심지어 불규칙한 시계열 데이터에선 LSTM보다 성능이 좋지 않았습니다.

그러므로 SCINet은 (1) Long-term 예측이나 (2) 시계열적인 특성이 존재하는 데이터에서 사용하기에 적절하다는 것을 알 수 있습니다.

이러한 성능 저하는 본 논문의 가정이 Down sampling(ex. Split)을 진행해도 전반적인 시계열 특징을 보장하는 것으로 하기 때문에 이와 반대로 Noise가 존재한다면 Down sampling 과정에서 잘못된 편향에서 영향을 받을 수 있기 때문인 것으로 파악된다.

그래서 이 논문에 대한 추후 연구로,

SFINet이라 해서 Noise가 있는 Real Data에서도 강건한 모델을 구현하는 연구를 진행했고, 공간적 정보를 함께 활용하는 SCINet 구조 모델인 Spatial-Temporal Interactive Dynamic Graph Convolution Network for Traffic Forecasting이라는 연구도 함께 살펴보시면 좋을 듯 싶습니다.