이번 글에서는 앞으로 자주 다루게 될 딥러닝에 대해 개괄적으로 다뤄보도록 하겠습니다.

[Deep Learning]

딥러닝이란 무엇일까요??

딥러닝은 머신러닝과 Deep Neural Network 모델을 합친 것이라고 이해할 수 있습니다. 딥러닝은 결국 머신러닝의 일부이고 따라서 머신러닝의 개념들이 모두 딥러닝에서도 사용됩니다.

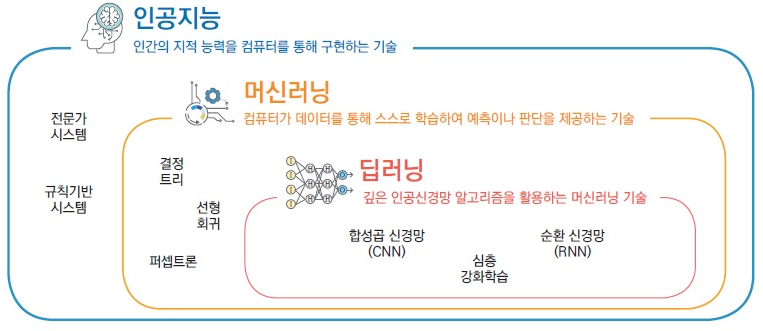
train/test, parametic learning, weight update.. 등등의 머신러닝 개념을 똑같이 사용하지만 Deep Neural Network라는 것이 딥러닝의 특징이라고 할 수 있습니다.

그럼 딥러닝을 왜 사용할까요?

결국엔 딥러닝이 성능이 좋기 때문에 사용하는 거고, 딥러닝이 성능이 좋은 이유는 딥러닝 모델이 내재적으로 가지고 있는 Feature extraction 때문입니다.

머신러닝은 Feature engineering을 분석가가 직접 수행해야 하기 때문에 한계가 있는 반면, 딥러닝은 모델이 직접 Feature extraction 하기 때문에 일반적으로 성능이 좋습니다.

하지만 이러한 특징 때문에 주의할 점도 있습니다.

바로 딥러닝은 ML보다 더 많은 학습 데이터를 필요로 한다는 것입니다. 딥러닝은 데이터가 충분하지 않으면 바로 오버피팅되어버립니다.

또한 딥러닝은 ML보다 더 많은 computing resource(GPU, TPU)를 필요로 합니다.

따라서 정형 데이터의 경우 머신러닝 특히 lightGBM이 더 좋은 성능을 보이기 때문에 굳이 현업에서도 가성비를 생각하여 라이트한 머신러닝을 쓰지 헤비한 딥러닝을 쓰려고 하지 않습니다.

다만 딥러닝은 컴퓨터 비전, 자연어처리, 음성파트 등 비정형 데이터 처리에서 매우 뛰어납니다. 이미지, 텍스트, 음성 데이터 분석의 경우 딥러닝이 좋기 때문에 위 분야에서 딥러닝을 많이 사용하고 이런 사례의 경우 굳이 white box일 필요가 없기 때문에 더욱 일반적으로 사용됩니다.

[Perceptron]

AI 즉, Artificial Intelligence 라는 단어 그 자체의 의미처럼 사람의 뇌를 본떠 인공지능을 만들자는 생각에서 출발한 Deep Neural Network 모델의 시작은 Perceptron이라는 모델이었습니다.

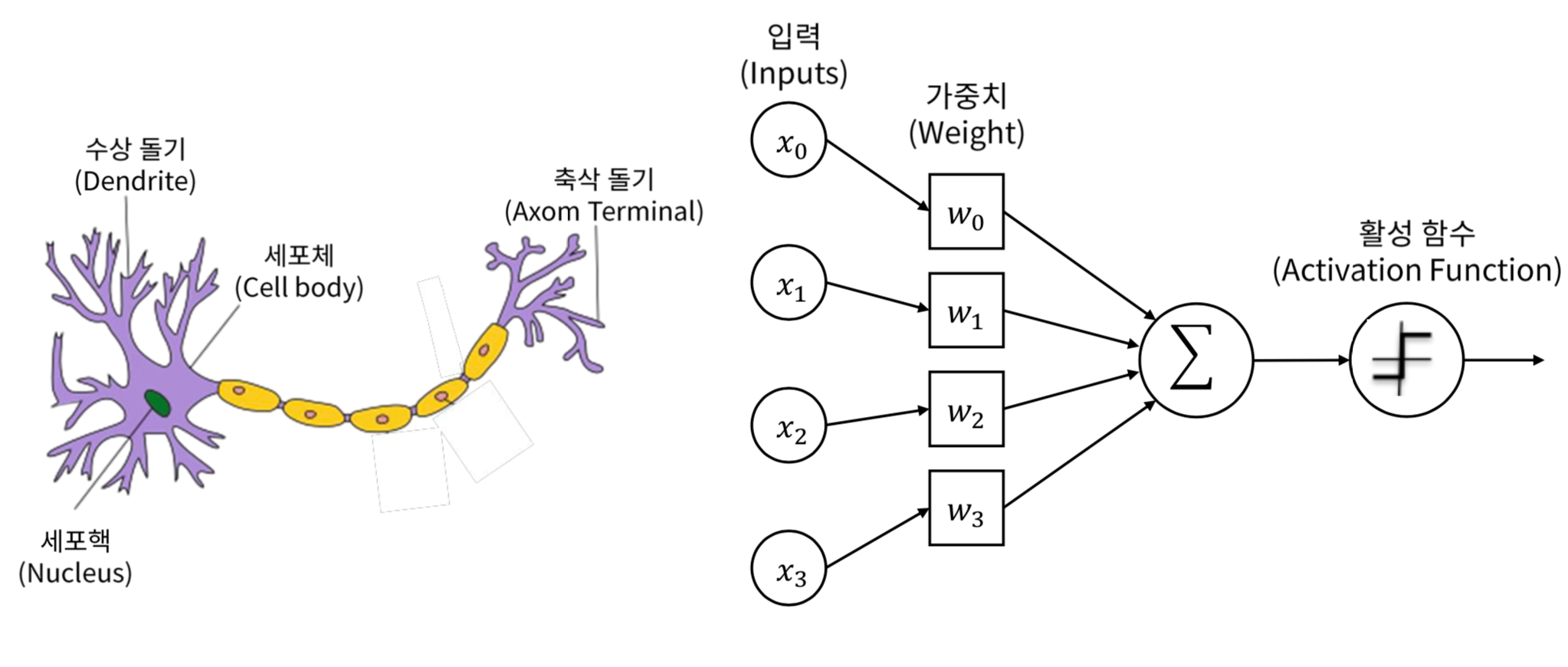
Perceptron은 프랑크 로젠블라트(Frank Rosenblatt)가 1957년에 제안한 초기 형태의 인공 신경망으로 뉴런의 구조에서 영감을 받아 다수의 입력으로부터 하나의 결과를 내보내는 알고리즘입니다.

뉴런은 수상돌기(입력) -> 신경세포체(처리) - 역치를 넘어가면 처리해줌 -> 축삭돌기(출력) 라는 과정으로 데이터를 처리하는데요.

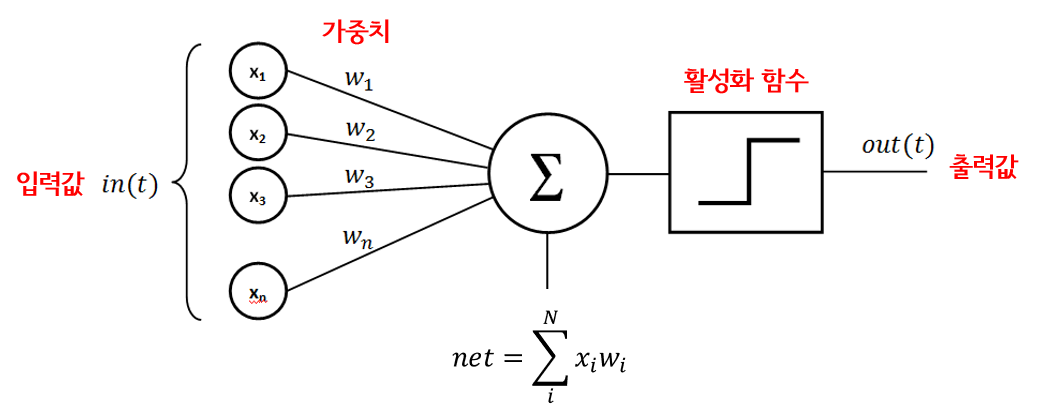
퍼셉트론의 구조도 이와 비슷합니다.

$x_1, x_2, x_3$는 데이터를 의미하고, $w_1, w_2, w_3$는 가중치를 의미합니다.
그리고 이들이 선형결합 즉 $f(w_1x_1+w_2x_2+w_3x_3+bias)$ 형태로 $f$의 입력으로 들어가게 됩니다.

이때 만약 $bias$가 없다면 이 선형결합이 계속 원점을 지나기 때문에 $bias$도 함께 입력하여 다른 곳도 돌아다닐 수 있도록 해줘야한다.

그리고 이때 위 선형결합 식에서 $f$를 activation function(활성함수)이라고 한다.

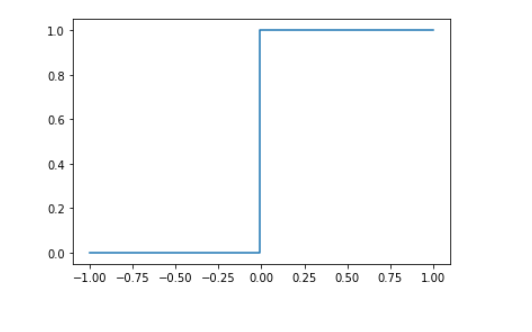
또한 이와 동시에 처음 등장한 활성함수는 step function으로 $w_1x_1+w_2x_2+w_3x_3+bias$라는 식의 값이 0을 넘으면 1, 아니면 0을 반환한다

하지만 퍼셉트론과 같은 Single Neural Network는 $XOR$ 문제를 해결하지 못한다는 단점을 가지고 있다!

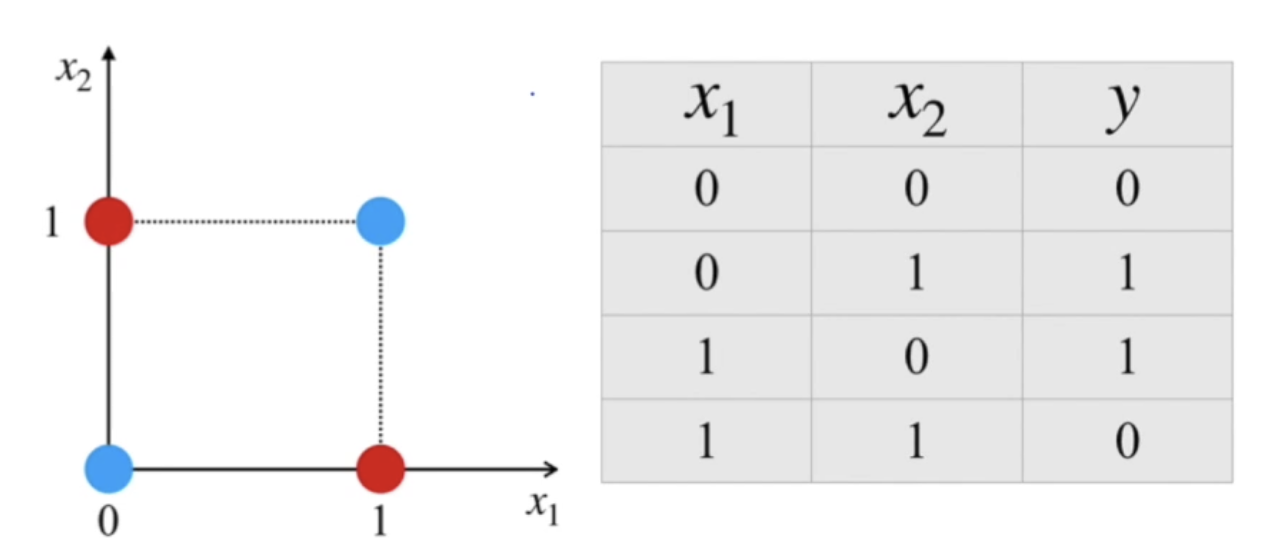
예를 들어 위와 같이 빨간 점과 파란 점 데이터를 분류하는 문제를 해결할 때 Single Neural Network은 하나의 선만으로 분류해야하는데 위 데이터에선 어떤 선을 그어도 올바르게 분류할 수 없다. 즉 비선형 데이터의 경우 해결할 수 없다는 특징을 가지고 있다.

[Multi Layer Perceptron(MLP)]

퍼셉트론의 위 단점을 해결하기 위해 또다시 사람의 뇌에서 영감을 받아 퍼셉트론들로 층을 구성한 다음 나열한 MLP 모델이 등장했다.

즉, MLP는 퍼셉트론을 쌓아서 구조적으로 위 문제를 해결하고자 하였다.

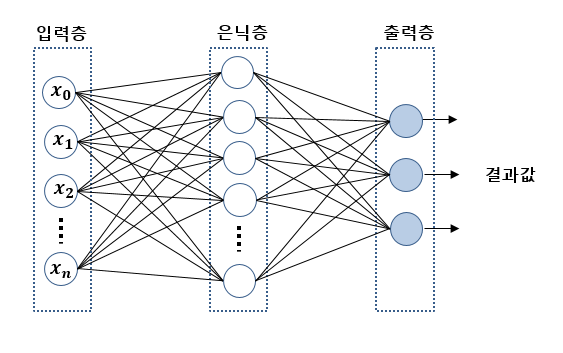
MLP에선 각 퍼셉트론을 동그라미로 나타내며 노드라고 한다.

각 노드들의 쌓이는걸 layer라 하고, 각 레이어들을 여기서 입력층, 은닉층, 출력층이라고 하고 각 노드는 fully connected 되어 있습니다.

또한 각 노드에는 앞에서 다뤘듯 활성함수가 정의되어있다.

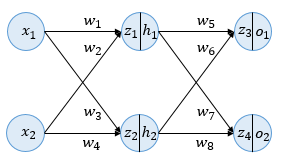
이렇게 하면 뭐가 좋냐면 $z_1$에서 합친 선형결합한 값을 $z_3$에서 한번 더 계산하기 때문에 다음과 같이 선을 그릴 수 있다.

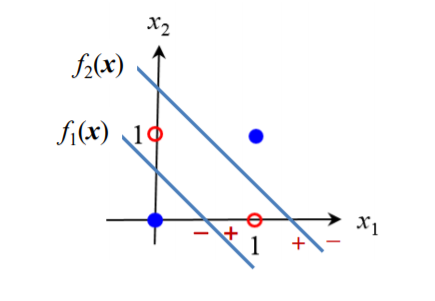
이렇게 $XOR$ 문제를 풀 수 있고 좋은 nonlinear classification 이 된다.

하지만! 선형문제를 두번 푼다고 해서 비선형문제를 풀 수 없겠죠?
그래서 활성함수를 nonlinear function으로 설정해서 이 문제를 해결해야 한다.

여기서 나온 활성함수가 바로 시그모이드 함수이다.

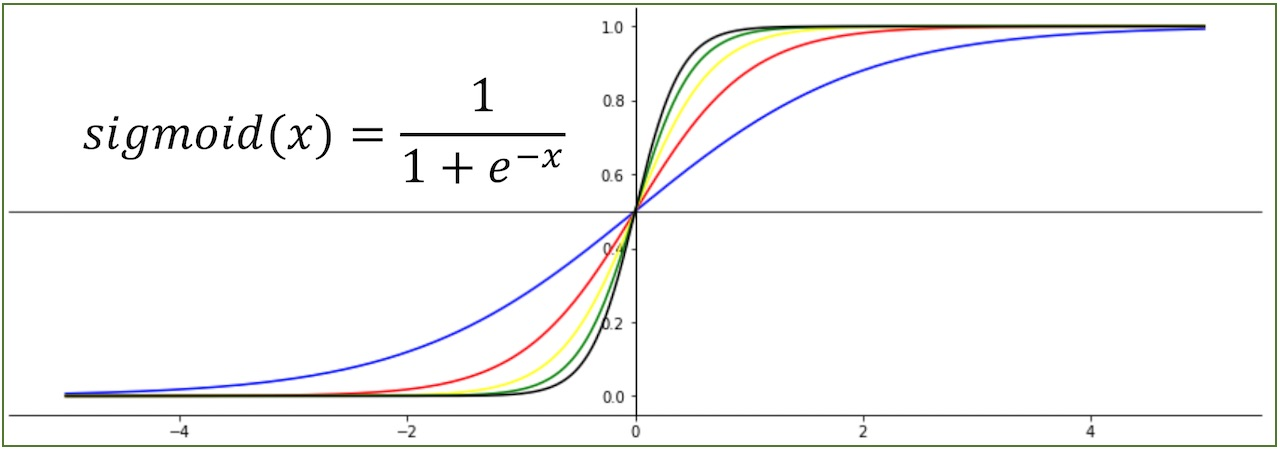
이 시그모이드 함수의 특징은 $x$에 입력되는 애들이 무슨 짓을 하더라도 결과값이 0과 1사이로 나온다는 것이다.

따라서 굉장히 많은 가중치가 합쳐져도 0과 1사이 값이 나오니깐 수치적으로 안정화되서 학습이 잘된다.

두번째 특징은 나중에 최적화를 배우면 최적화를 위해 미분을 써야하는데 시그모이드 함수는 미분을 하기 쉽다는 특징이 있습니다.

하지만 최근에는 여기서 더 발전한 활성함수인 ReLu function(Recified Linear Unit)을 사용합니다.

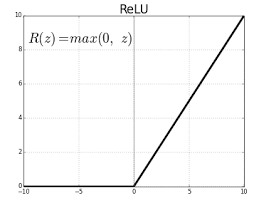
이 함수도 역시 미분할 경우 0보다 작으면 0, 0보다 크면 1의 값을 가져서 미분도 되게 쉽고 음수 부분을 모두 0으로 제거하기 때문에 업데이트 관점에서 되게 좋습니다.

시그모이드 함수의 경우 양 끝의 기울기가 거의 0에 가깝기 때문에 이 부분에서 업데이트가 안되는데 ReLu 함수는 이 문제를 해결할 수 있습니다.

[feed forward]

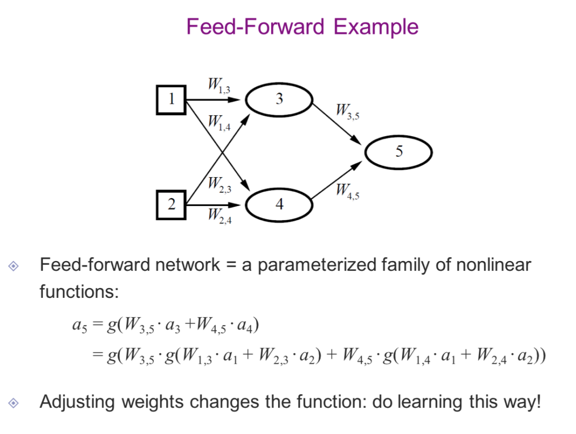
feed forward의 예시는 위와 같은데, 예를 들어 위 식에서 $g$가 앞에서 살펴본 ReLu 함수라면 노드 3에선 다음과 같이 계산된다.

이때 $W_{1,3} \ a_1+W_{2,3} \ a_2 + bias$가 0보다 크면 해당 값이, 0보다 작으면 0이 결과로 도출된다.

그리고 마지막 출력층에서 Node5에서는 다음과 같이 식으로 정리된다.

이 방식처럼 입력층->히든층->출력층으로 활성함수를 지나면서 값이 업데이트 되는 게 feed forward입니다.

그래서 MLP의 feed-forward는 선형 식의 결과가 선형 식에 들어가고 또 다시 선형 식으로 들어가며 진행되는 방식에, nonlinear 한 활성함수를 씌우는 것입니다.

최종적으로 feed forward를 통해 "합성합수"의 형태로 결과가 도출되게 됩니다.

그리고 이런 모델을 Neural network 라 하고, 은닉층이 2개 이상이면 Deep Neural network(DNN) 이라고 합니다.

여기까지 딥러닝과 머신러닝의 차이, 퍼셉트론, $XOR$ Problem, MLP, 활성화함수, feed forward까지 간략하게 다뤄보았습니다. 2편에서는 Output / Loss function과 역전파, 딥러닝 학습방법에 대해 다뤄보도록 하겠습니다.