[Classification Problem] Ensemble 종류 (Bagging, Boosting, Stacking)

Ensemble 종류

---

• Bagging : Reduce the Variance
  • Stacking : Use another prediction model
• Boosting : Reduce the Bias

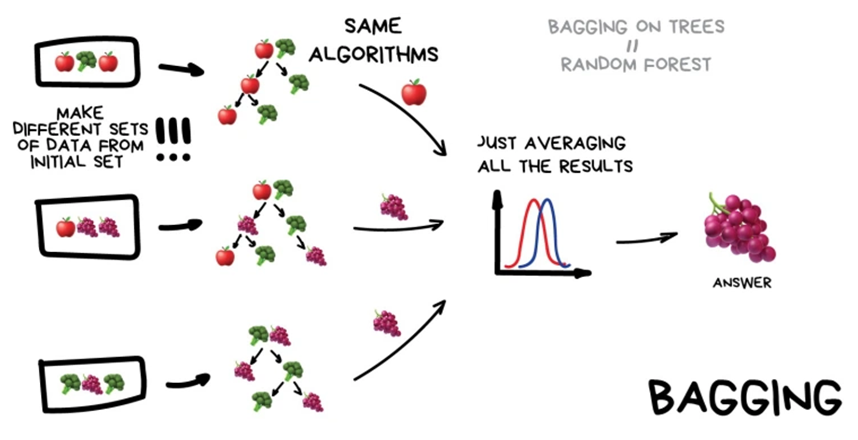
Bagging

---

• Reduce the Variance
  
• Bagging : Bootstrap Aggregating
  • Bootstrap : 표본에서 추가적으로 표본을 복원 추출하고 각 표본에 대한 통계량을 다시 계산하는 것
  • N개의 Data가 있으면 N개를 Randomly하게 뽑아내서 새로운 Data Set을 구성함
    
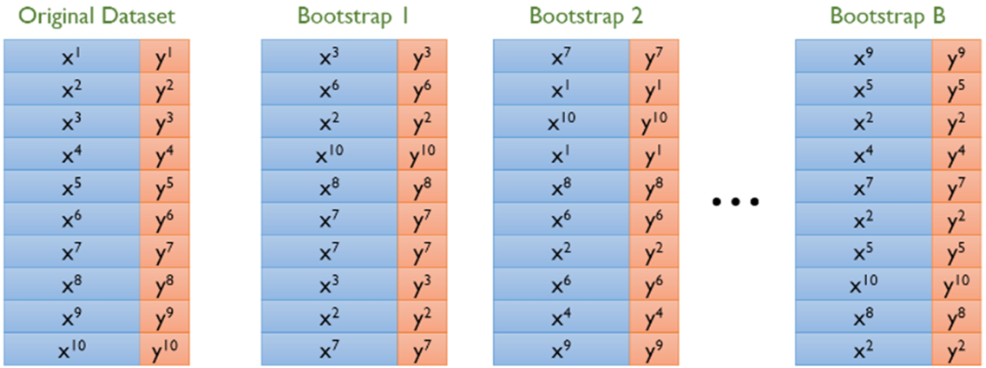
• Bootstrap을 진행하면 확률 상 뽑히지 못한 데이터는 36.8%가 됨
  $p = \left(1 - \frac{1}{N}\right)^N \rightarrow \lim_{N \to \infty} \left(1 - \frac{1}{N}\right)^N = e^{-1} = 0.368$
  

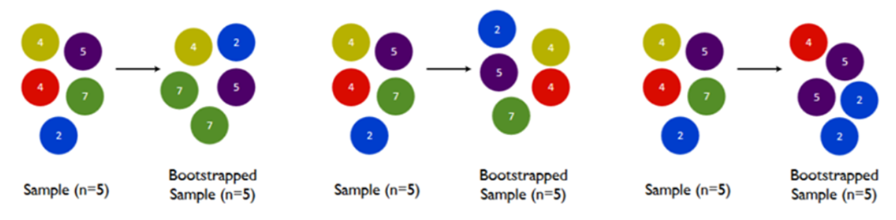
Model Result Aggregating Method

Majority voting

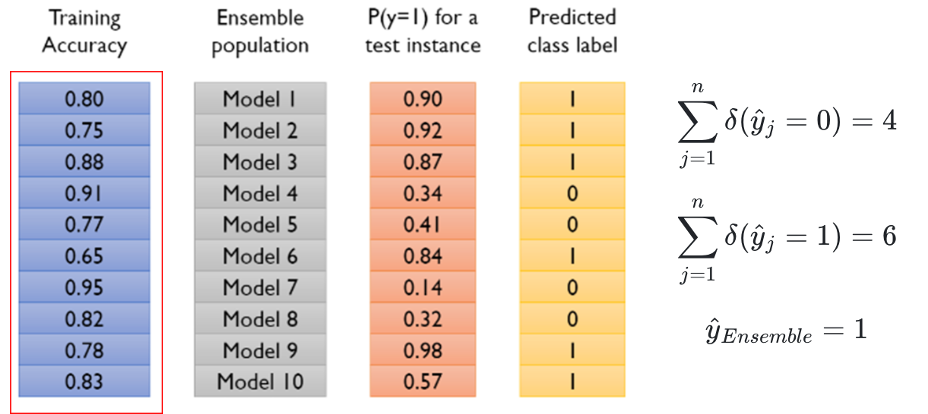
Weighted voting 1

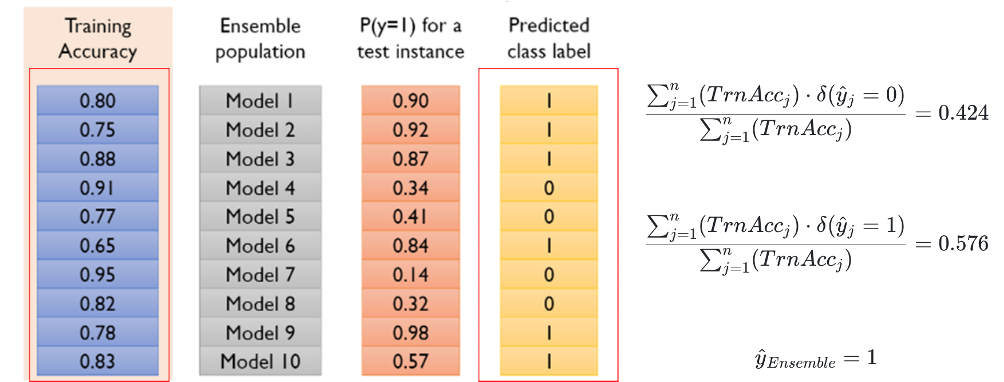
Weighted voting 2

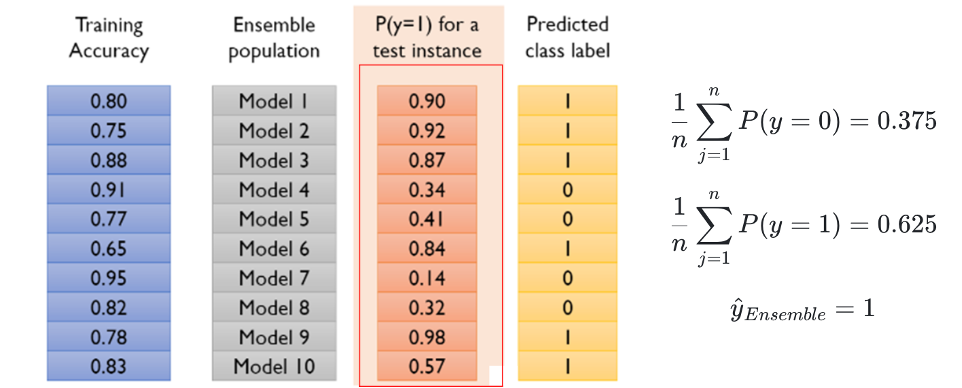
Model Result Aggregating Method

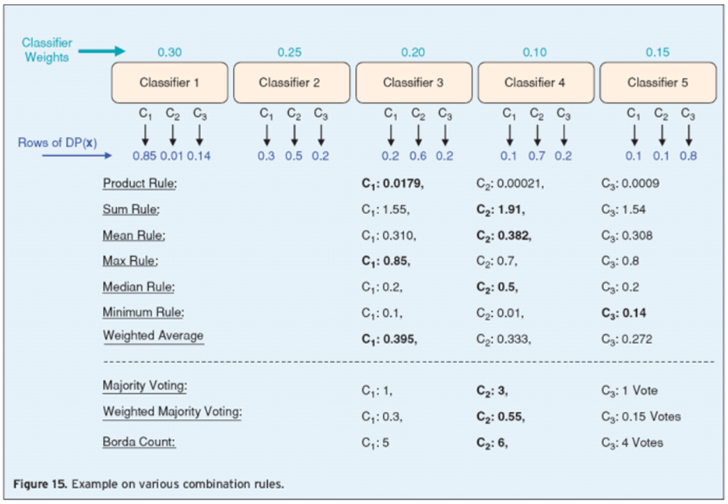
Stacking

---

• Use another prediction model
  

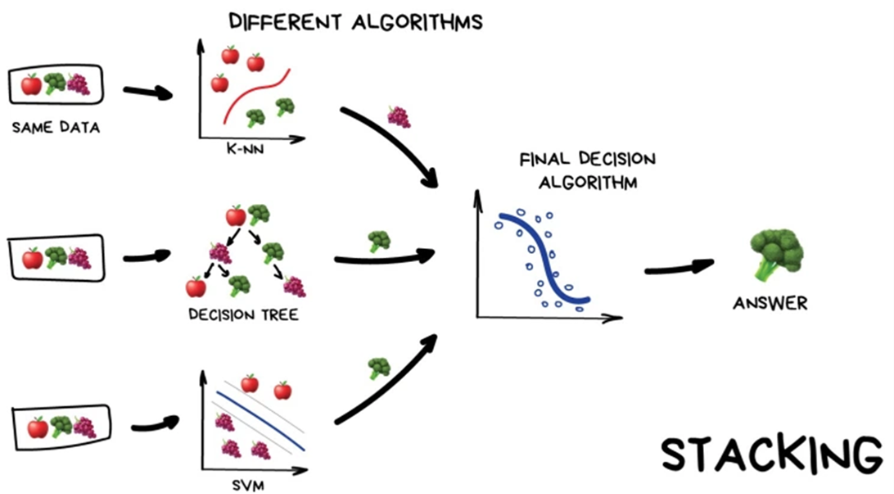
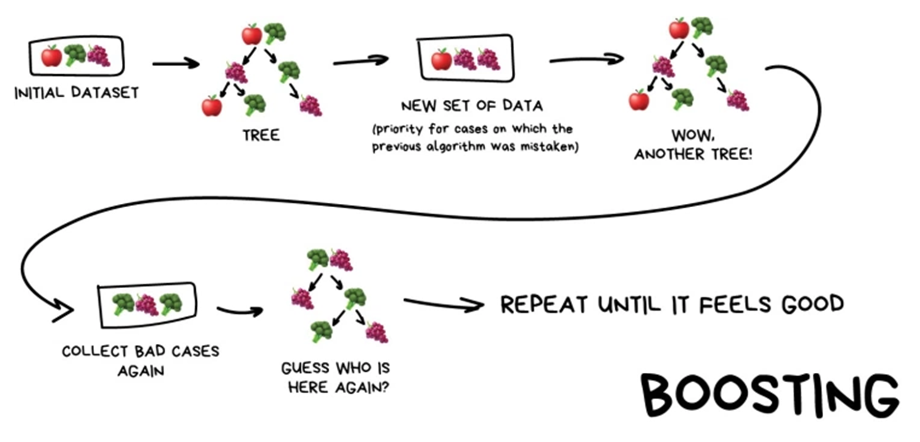
Boosting

• Reduce the Bias
• 처음에 못 맞춘 데이터에 대해서 우선순위를 부여해 학습확률을 높여서 맞출 때까지 수행