[Classification Problem] Random Forest

Random Forest

---

• Random Decision Forests (1995) – Bell Labs의 Tin Kam Ho 박사
  (단순 여러 개의 Decision Tree 를 랜덤하게 고른 Feature로 학습한 후 조합)
• Random Forests (2001) – UC Berkeley 통계학과 Leo Breiman 교수
  (Random Decision Forests + Bagging 기법 추가)

알고리즘

• A specialized bagging for decision tree algorithm
• Two ways to increase the diversity of ensemble (다양성 증가)
  

Two ways to increase the diversity of ensemble

• Bagging

• Randomly chosen predictor variables

• Tree는 작은 Bias와 큰 Variance를 갖기 때문에, 매우 깊이 성장한(Depth가 깊은) 트리는 훈련 데이터에 대해 Overfitting 하게 됨

• 한 개의 Tree의 경우 훈련 데이터에 있는 Noise에 대해 매우 민감함

  • Tree들이 서로 상관화(correlated)되어 있지 않다면 여러 Tree들의 평균은 Noise에 대해 강인해짐
  • 상관화를 줄이는 방법은 Randomly Chosen (행 & 열 모두)
  • 반면, Forest를 구성하는 모든 Tree들을 동일한 데이터 셋으로만 훈련시키게 되면, Tree들의 상관성은 커짐

• 따라서 Bagging은 서로 다른 데이터 셋들에 대해 훈련 시킴으로써, Tree들을 비상관화 시켜주게 됨

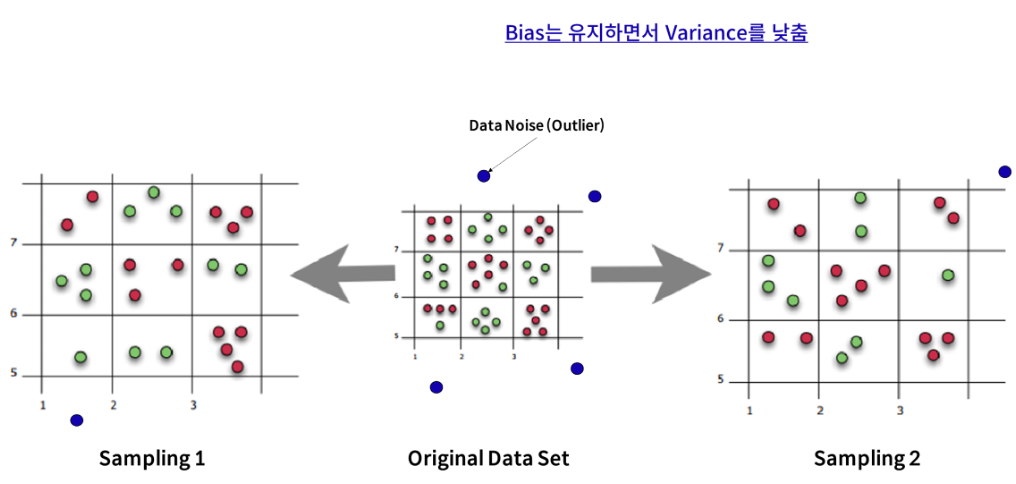
  • Bias는 유지하면서 Variance를 낮춤
    

Out Of Bag

• Bootstrap을 진행하면 확률 상 뽑히지 못한 데이터는 36.8%가 됨
• 뽑히지 못한 Data를 활용하여 Model의 성능을 측정함
• 대게 Model의 성능을 측정할 때, Train set과 Valid set을 나눔
• 하지만 Random Forest의 경우 Valid set을 나눌 필요가 없음 → 뽑히지 못한 36.8% OOB Data 활용 !

Out Of Bag 활용 Feature Importance Score

Step 1 : Compute the OOB error for the original dataset (Bootstrap 시 뽑히지 못한 36.8% Data 활용)

Step 2 : Compute the OOB error for the datatset in which the variable $x_i$ is permuted $p_i$

• 셔플
  

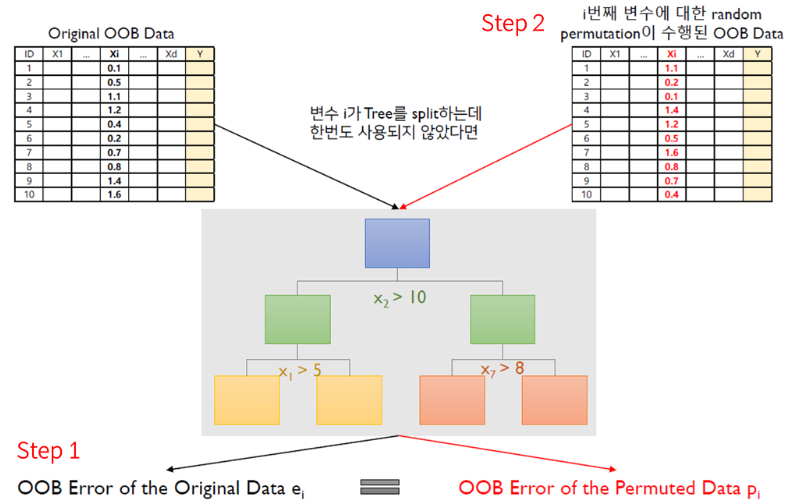
Step 3 : Compute the variable importance based on the mean and standard deviation of over all trees in the population

• 성능이 같거나 작으면 중요하지 않은 변수, 크면 중요한 변수
  

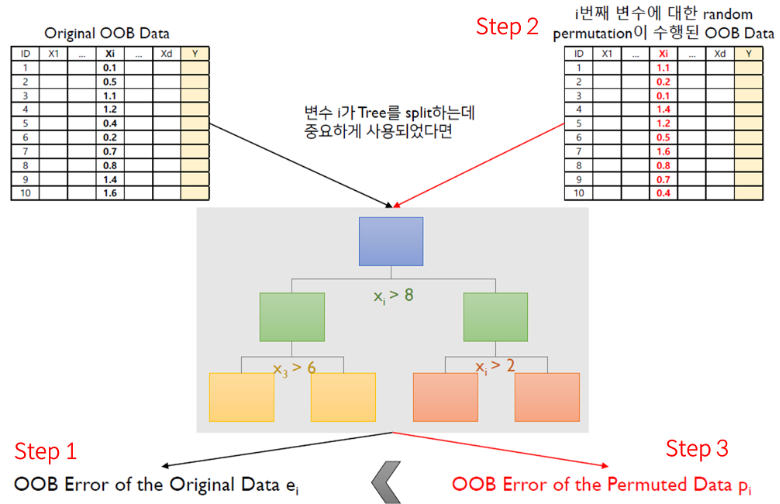
랜덤 포레스트에서 변수의 중요도가 높다면?

• 1) Random permutation 전-후의 OOB Error 차이가 크게 나타나야 하며,

• 2) 그 차이의 편차가 적어야 함

• m번째 tree에서 변수 i 에 대한 Random permutation 전후 OOB error의 차이

  $d_{i}^{m} = p_{i}^{m} - e_{i}^{m}$

• 전체 Tree들에 대한 OOB error 차이의 평균 및 분산

  $\bar{d}_{i} = \frac{1}{m} \sum_{i=1}^{m} d_{i}^{m}, \quad s_{i}^{2} = \frac{1}{m-1} \sum_{i=1}^{m} (d_{i}^{m} - \bar{d}_{i})^2$

• i 번째 변수의 중요도:

  $v_{i} = \frac{\bar{d}_{i}}{s_{i}}$
  • 어떤 트리에서는 중요한데 어떤 트리에서는 중요하지 않음 → 분산 ↑ → 중요도 ↓

Feature Importance Score 예시

![]()
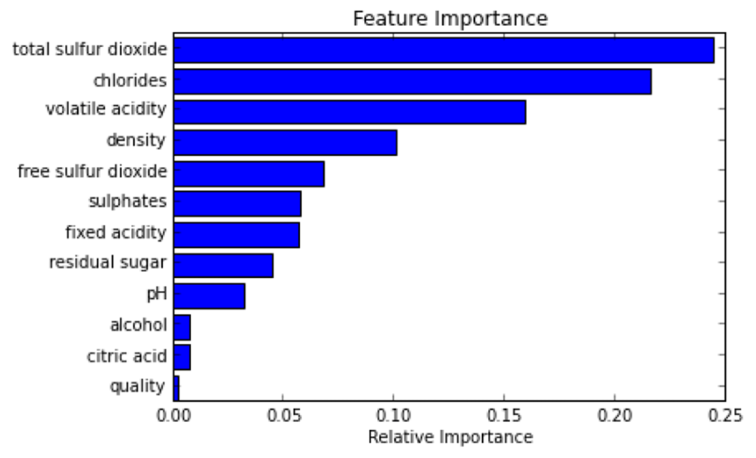