- Overfitting을 방지하기 위해서 Feature Selection 수행
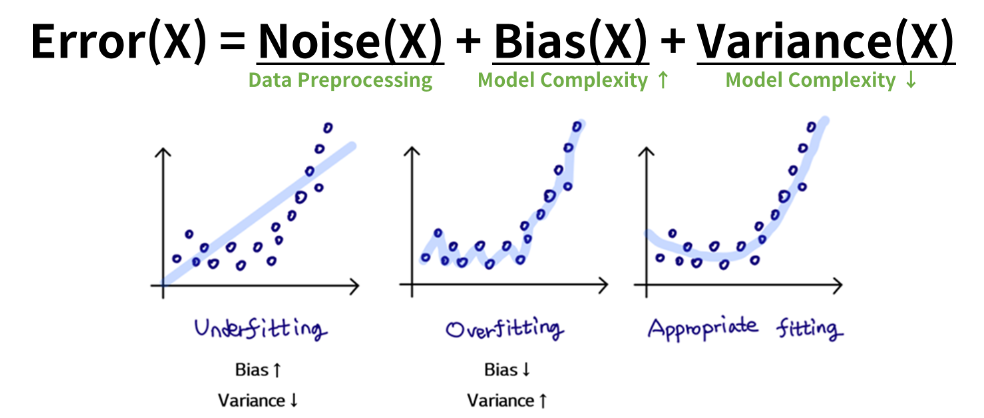
- Underfitting일 때는 모델의 정확도가 낮기 때문에 Feature Selection이 의미가 없음
- Train Set 정확도가 높지만 Test Set의 정확도가 낮을 때 Feature Selection 수행
- Feature의 수가 많아지면 많아질수록 Model Complexity(복잡도)는 높아짐
- Model Complexity가 높아지면 높아질 수록 Bias는 낮아 지는 반면 Variance가 높아짐
- 따라서, Feature Selection을 활용하여 Bias와 Variance의 Trade-off 최적점을 도출 해야함
Exhaustive Search (완전 탐색)
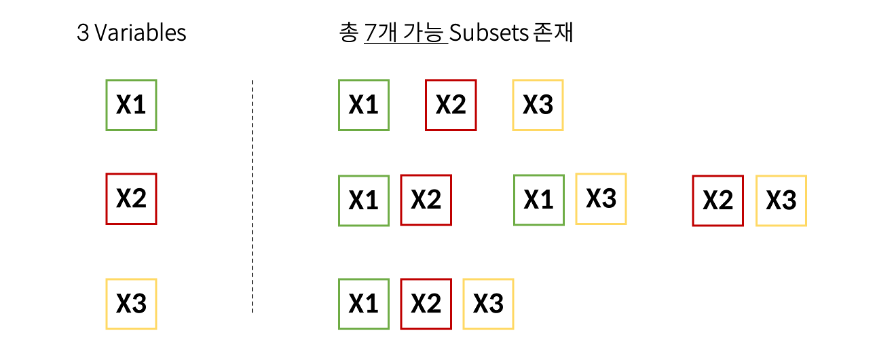
- Feature의 최적 조합을 찾아냄
- 경우의 수는 𝟐^𝒑-1 (단, P는 Feature의 개수)
- 총 7개 Subsets의 정확도를 바탕으로 최적의 조합을 찾아냄
- Training Set의 정확도 보다 Test Set의 정확도를 봄
- 이러한 Exhaustive Search (완전 탐색) 방법은 시간이 너무 오래 걸림
- 시간이 Exponential 하게 증가함
Forward Selection
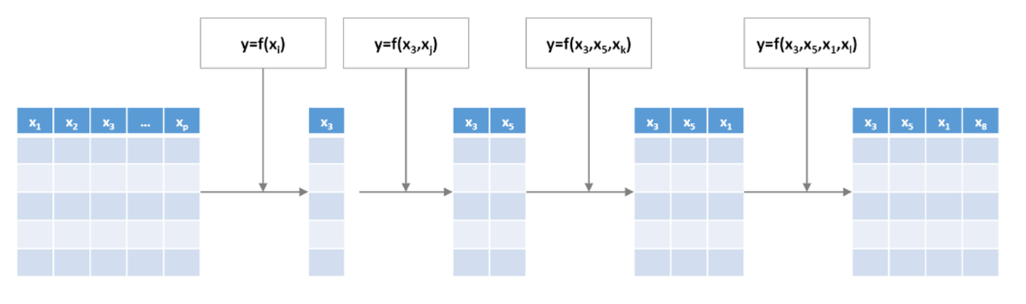
- Multiple linear Regression에서의 Forward Selection
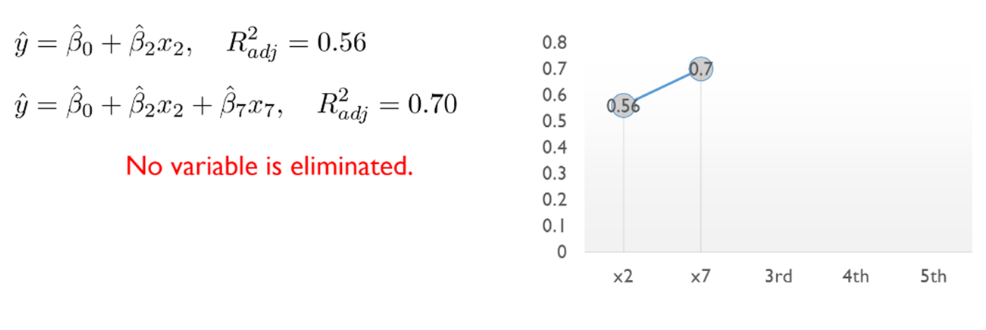
- 처음에는 variable이 없이 시작해서 하나씩 중요한 변수들을 Sequentially 추가함
- 한번 선택된 variable은 절대 지우지 않음
- 한번 선택된 variable은 절대 지우지 않음
예시 (8개 Variables)



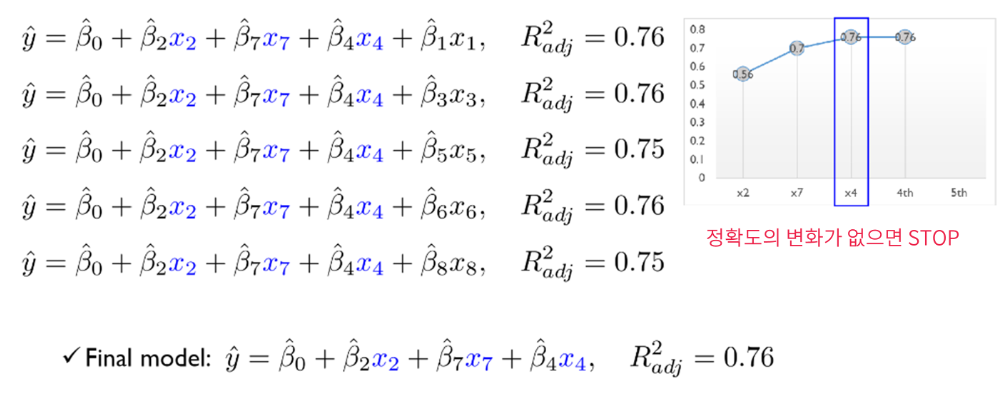
Backward Elimination
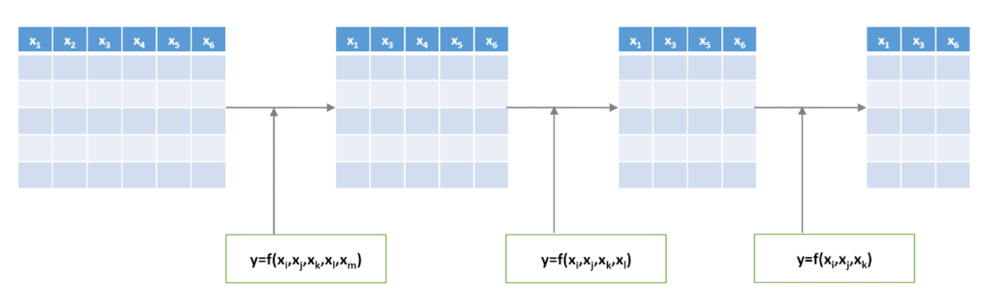
- Multiple linear Regression에서의 Backward Elimination
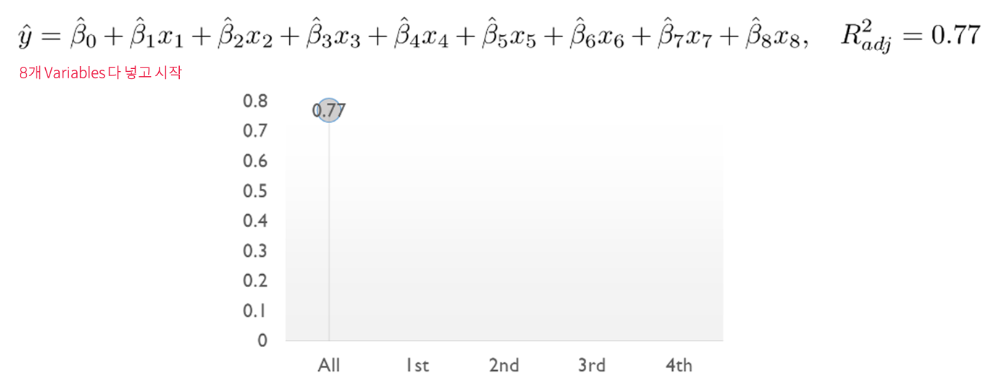
- 처음에는 모든 variables을 사용하고, 정확도에 영향을 미치지 않는 불필요한 variable을 sequentially 제거함
- 한번 제거된 variable은 절대 다시 선택하지 않음
- 한번 제거된 variable은 절대 다시 선택하지 않음
예시 (8개 Variables)


Stepwise Selection
- Forward Selection과 Backward Elimination을 번갈아 가며 수행함
- Forward Selection과 Backward Elimination 보다 시간은 오래 걸릴 수 있지만, 최적 Variable Subset을 찾을 가능성이 높음
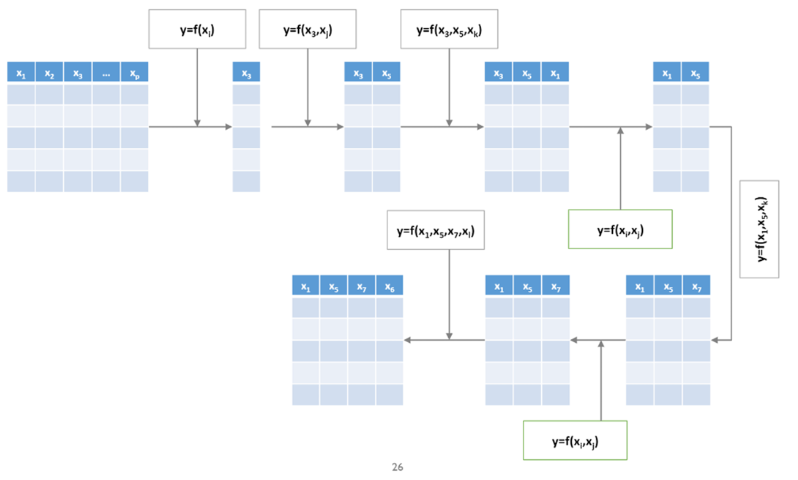
예시 (8개 Variables)



세가지 방법 정리