[Regression Problem] Model 평가 및 지표 해석

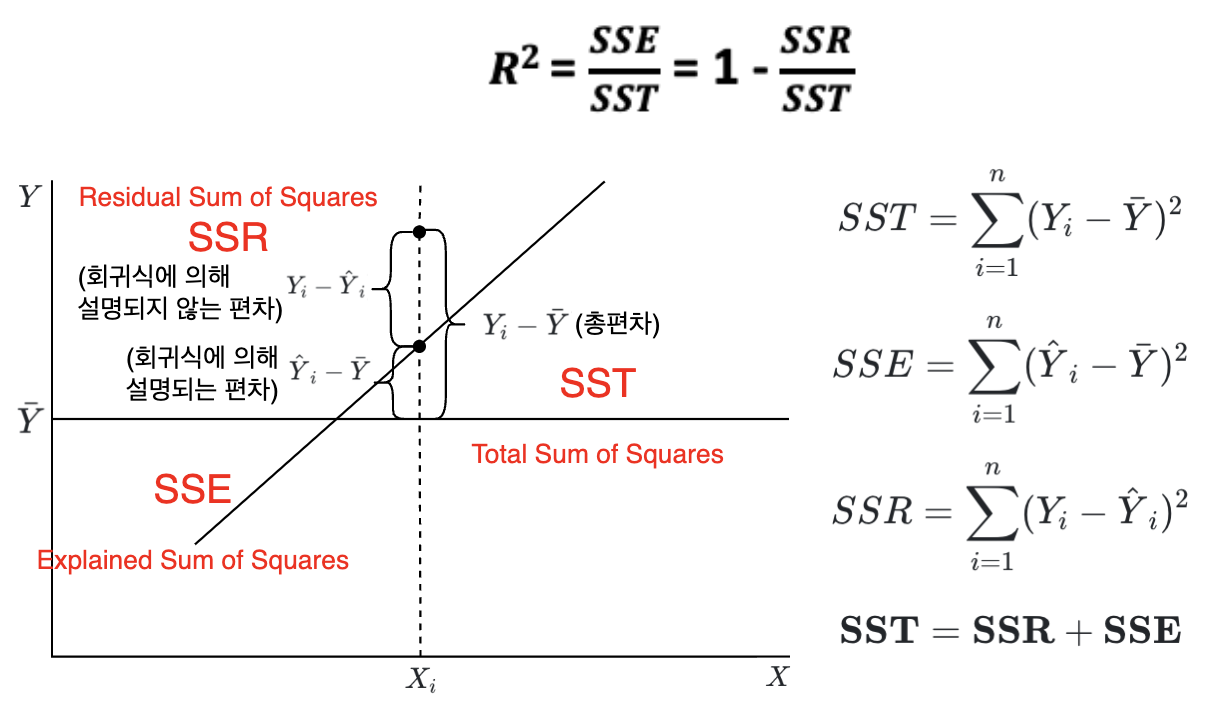
R-Squared

---

• Regression Model의 정성적인 적합도 판단
• $𝑹^𝟐$ 는 평균으로 예측한 것에 대비 분산을 얼마나 축소 시켰는지에 대한 판단
• 보통은 아래의 수식과 달리 Correlation($𝒚$, $\hat𝒚$)의 제곱으로 표현함
• 정성적인 판단이 필요한 이유는 통상적으로 Model의 예측력을 판단하기 위함
• 0 ~ 1 사이의 값을 갖고 1에 가까울수록 좋은 모델
• 총 제곱합 (SST), 회귀 제곱합 (SSR), 잔차 제곱합 (SSE)을 이용해 $R^2$을 구할 수 있음
  

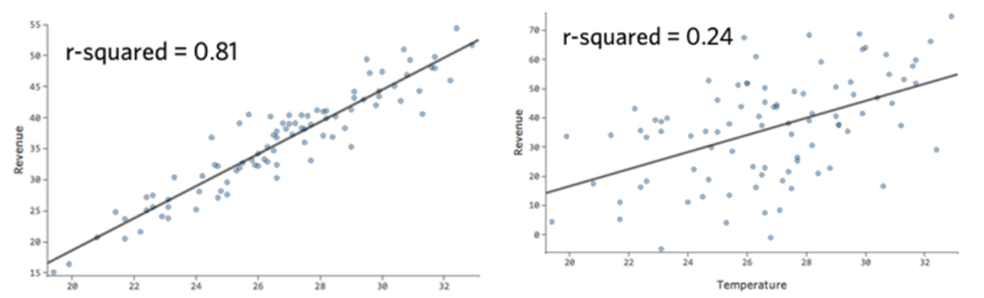
과연 $𝑹^𝟐$ 가 어느 정도 수치일 때 쓸 만한 모델일까?

• 현업에서 $𝑹^𝟐$ 가 0.3 이상인 경우를 찾기 힘듦
• $𝑹^𝟐$ 의 경우 0.25 정도도 유 의미하다고 판단함
  

성능지표1 : Average Error – 평균오차

---

• 잘못된 정량적인 방법
• 실제 값에 비해 과대/과소 추정 여부를 판단
• 부호로 인해 잘못된 결론을 내릴 위험이 있음
  $\text{Average error} = \frac{1}{n} \sum_{i=1}^{n} (y - y’)$

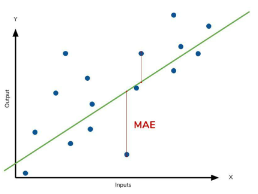
성능지표 2 : MAE – 평균 절대 오차

---

• Mean Absolute Error (MAE)
• 실제 값과 예측 값 사이의 절대적인 오차의 평균을 이용
  $\text{MAE} = \frac{1}{n} \sum_{i=1}^{n} |y - y’|$
• 

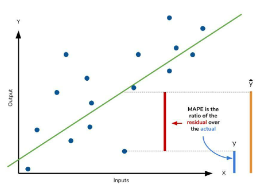
성능지표 3: MAPE – 평균 절대 비율 오차

---

• Mean Absolute Percentage Error (MAPE) – 평균 절대 비율 오차
• 실제 값 대비 예측 값이 얼마나 차이가 있는지를 %로 표현
• 상대적인 오차를 추정하는데 주로 사용

• 

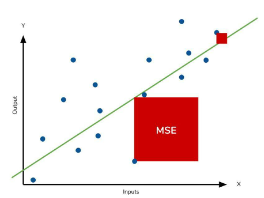
성능지표4&5 : (R)MSE

---

• (Root) Mean Squared Error
• 부호의 영향을 제거하기 위해 절대값이 아닌 제곱을 취한 지표

• 

Model 평가 및 해석 순서

---

• 모델 성능 체크 – 정성, 정량
  • 모델 성능이 나오지 않을 경우 데이터 품질 check
  • Model Loss Function은 평가지표로 하는 것이 좋음
• P-value를 확인하여 의미 있는 변수 추출
• $\beta_i$ 활용, X 가 1단위 증가 당 Y 에 얼마나 영향을 미치는지 판단