[Regression Problem] Regularized Model-Ridge

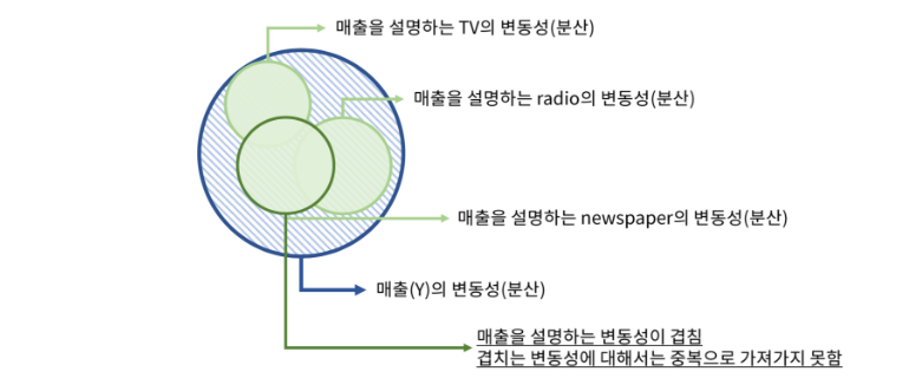
Ridge Regression

---

• $β^𝟐$ 에 Penalty Term을 부여하는 방식

• Penalty Term을 추가한 Regularized Model의 경우 Feature 간 Scaling이 필수
  

• Regularization은 모델의 복잡도를 조절하여 과적합(overfitting)을 방지하는 방법

  • 주어진 데이터에서 최적의 $\beta$ 값을 찾기 위해 목적함수를 최소화

• (1) - Loss Function, (2) penalty Term

• $\lambda$: Regularization 파라미터로, 두 목적 간의 균형을 조절

• 만약 $β_1$, $β_2$가 중요한 feature라면 penalty를 받더라도 값을 유지하고 다른 $β$들의 값이 낮아져 최소화시킴

Hyperparameter λ의 영향

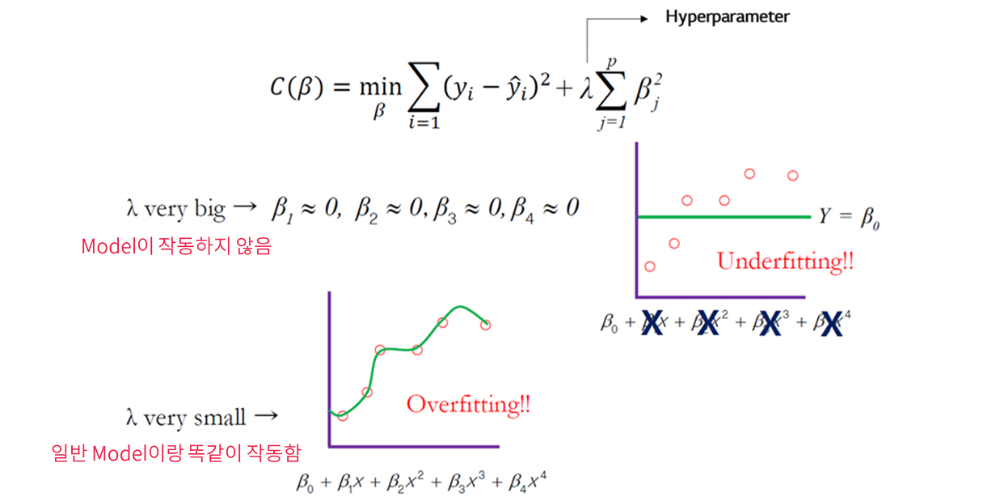
• λ very big: $\beta_1 \approx 0, \beta_2 \approx 0, \beta_3 \approx 0, \beta_4 \approx 0$ -> Model이 작동하지 않음 (Underfitting)
• λ very small: 일반 모델과 동일하게 작동 (Overfitting)
• 적절한 λ를 찾는 것이 중요!

Regularization Example

• Regularization 적용 전후의 모델 성능 비교
  

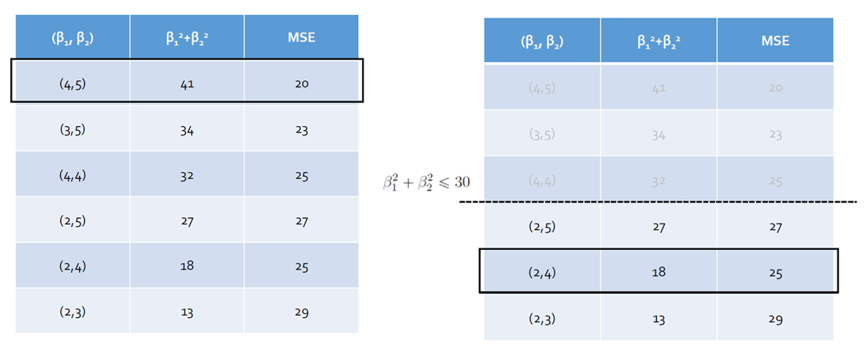
Penalty Term 부여 방식

• $β^𝟐$ 에 Penalty Term을 부여하는 방식 = $𝑳_𝟐$−𝑛𝑜𝑟𝑚 = $𝑳_𝟐$ Regularization
• 제곱 오차를 최소화하면서 회귀 계수 $β^𝟐$ 을 제한함
  

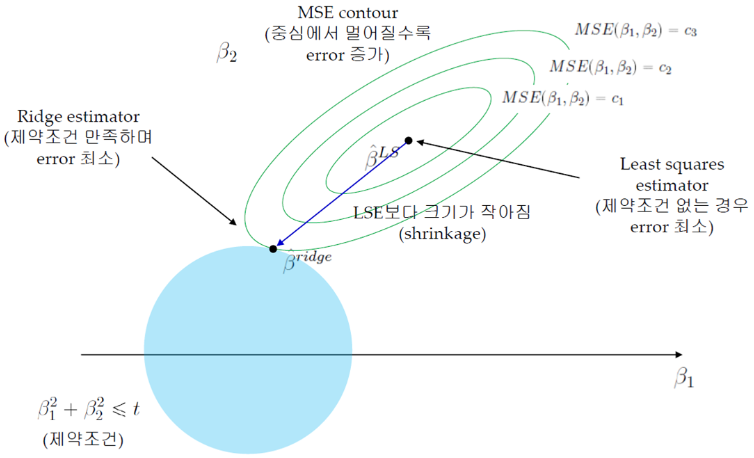
MSE Contour

• MSE Contour: 중심에서 멀어질수록 Error 증가
  ⠀⠀⠀⠀⠀⠀⠀⠀⠀→ Train Error를 조금 증가시키는 과정 (Overfitting 방지)
• Ridge Estimator와 MSE Contour가 만나는 점이 제약 조건을 만족하며 Error가 최소가 됨
  

해 찾기

• Ridge는 미분이 가능하기 때문에 Closed Form solution을 구할 수 있음
• 빠르게 해를 찾을 수 있다는 장점이 있음
  

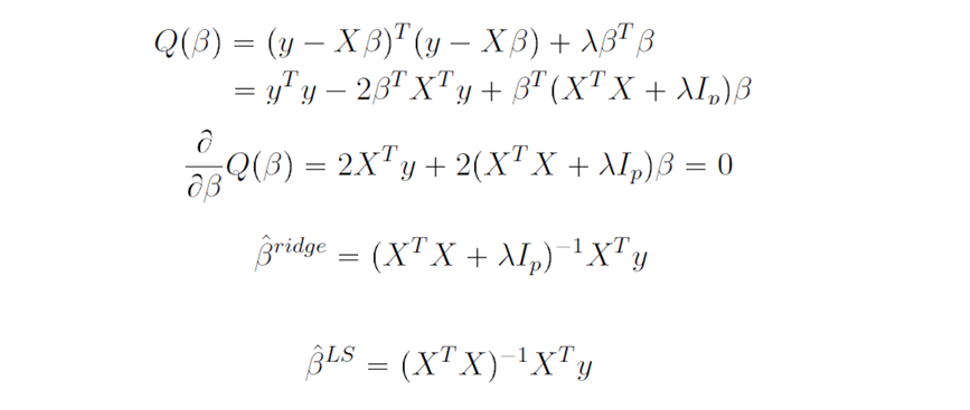
Ridge Regression 특징

• Ridge는 해 공간에서도 볼 수 있듯 Feature Selection은 되지 않음
• 하지만 불필요한 Feature는 충분히 0에 거의 수렴하게 만들어 버림
• Ridge Regression은 Feature의 크기가 결과에 큰 영향을 미치기 때문에 Scaling이 중요함
• 다중공선성(Multicollinearity) 방지에 가장 많이 쓰임