[Regression Problem] Regularized Model-LASSO

LASSO Regression

---

• Least Absolute Shrinkage and Selection Operator
• |β| = $𝑳_𝟏$−𝑛𝑜𝑟𝑚 = $𝑳_𝟏$ Regularization 에 Penalty Term을 부여하는 방식
  

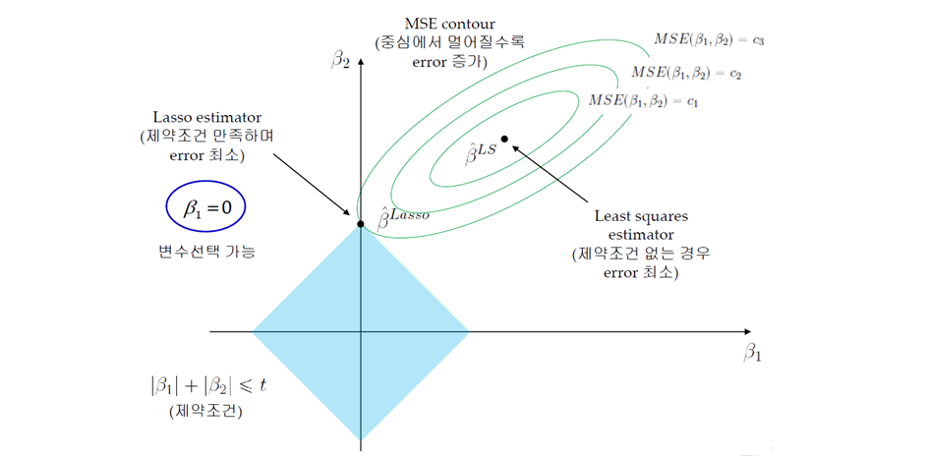
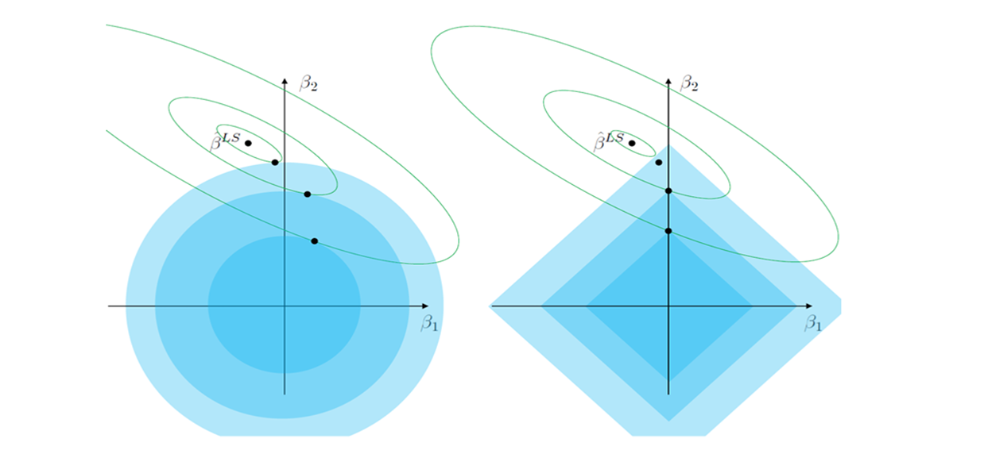
MSE Contour

• MSE Contour: 중심에서 멀어질수록 Error 증가
  ⠀⠀⠀⠀⠀⠀⠀⠀⠀→ Train Error를 조금 증가시키는 과정 (Overfitting 방지)
• LASSO Estimator와 MSE Contour가 만나는 점이 제약 조건을 만족하며 Error가 최소가 됨
• Feature Selection 가능
  

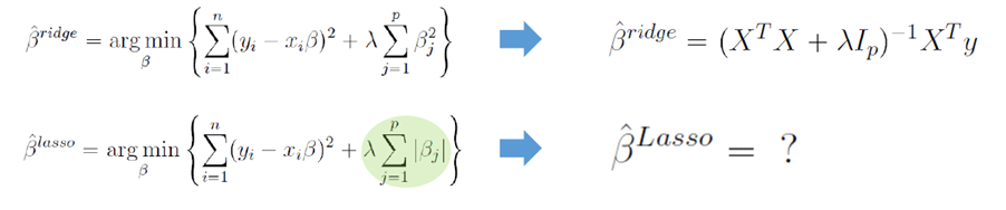
해 구하기 불가능

• Ridge Regression과 달리 Lasso Formulation은 Closed Form Solution을 구하는 것이 불가능
  • 절대 값이기 때문에 미분 불가능
• Numerical Optimization Methods 필요
  • Quadratic Programming techniques (1996, Tibshirani)
  • LARS Algorithm (20224, Efron et al.)
  • Coordinate descent Algorithm (2007, Fridman et al.)
  • Semi-differentiable
    

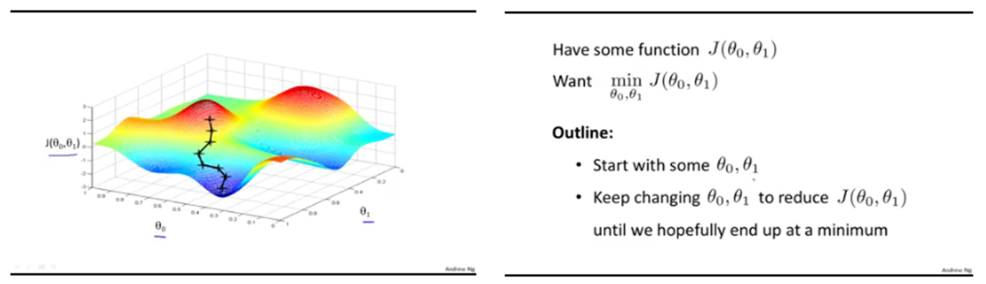
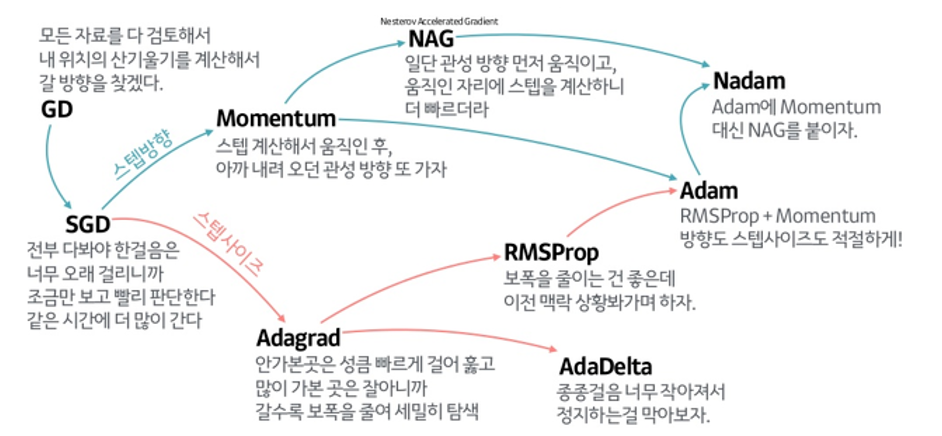
Gradient Descent: 경사 하강법

• Non-convex 경우 Gradient Descent를 활용하여 해(Loss가 가장 낮은)를 찾아 감
• 대부분의 non-linear regression 문제는 closed form solution이 존재하지 않음
• Closed form solution이 존재해도 수많은 parameter가 있을 때 Gradient Descent로 해결하는 것이 효율적
• 시작점이 중요하고 병렬로 진행됨
  

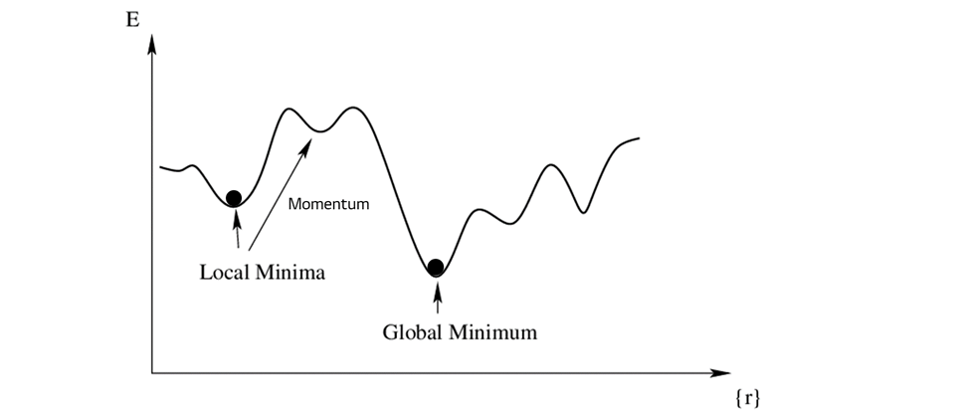
단점

• Local Minima에 빠질 수 있음
• 우리는 Global Minimum이 있는지 알 수 없음
• 최적의 해를 보장하지 않음
  

다양한 연구

• Global Minimum 을 보장하지 않기 때문에 현재까지도 다양한 연구가 이루어지고 있음
• Deep Learning의 Loss Function 최적화 시 매우 중요한 개념 (시작점이 중요함, 병렬 처리 가능)
  

LASSO Regression 특징

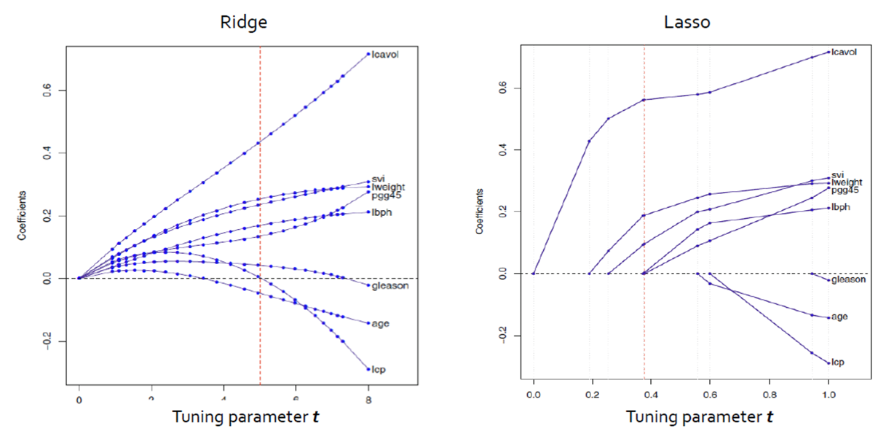
• Ridge와 LASSO 모두 t가 작아짐에 따라 (λ 가 커짐에 따라) 모든 계수의 크기가 감소함
• Ridge: 크기가 큰 변수가 더 빠르게 감소하는 경향을 보임
• LASSO: 예측에 중요하지 않은 변수가 더 빠르게 감소, t가 작아짐에 따라 예측에 중요하지 않은 변수는 0이 됨
  
  

Ridge vs Lasso

---

장단점

Ridge	Lasso
$L_2$ norm regularization	$L_1$ norm regularization
변수 선택 불가능	변수 선택 가능
Closed form solution 존재 (미분으로 구함)	Closed form solution이 존재하지 않음 (numerical optimization 이용)
변수 간 상관관계가 높은 상황 (collinearity)에서 좋은 예측 성능	변수 간 상관관계가 높은 상황에서 ridge에 비해 상대적으로 예측 성능이 떨어짐
크기가 큰 변수를 우선적으로 줄이는 경향이 있음