[Regression Problem] β(계수) 추정 법

Simple & Multi-Linear Regression

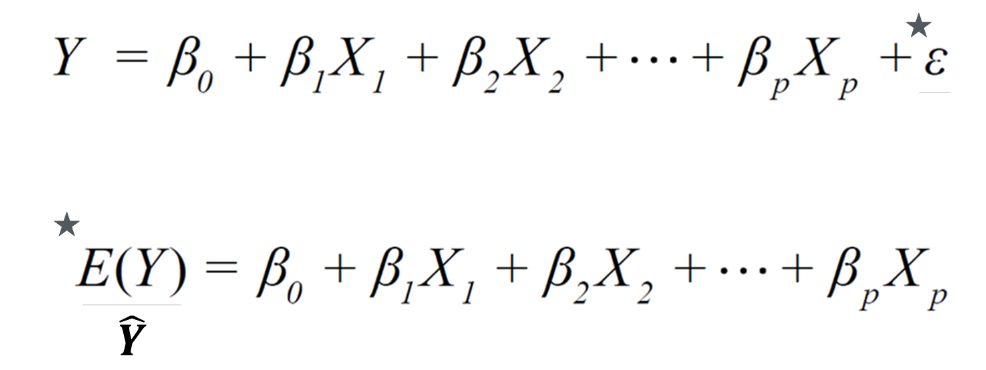
β(계수) 추정 법

---

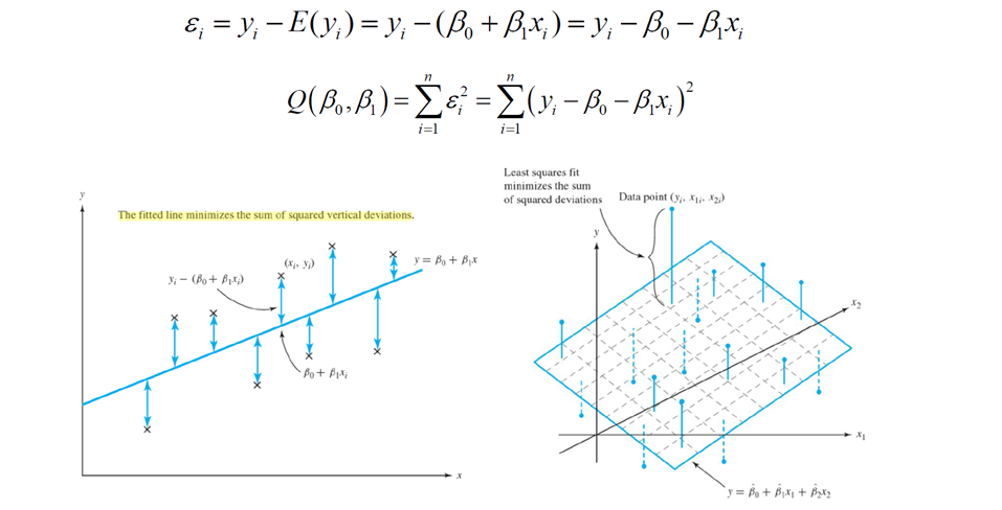
• 각 𝜷 에 대해 편미분을 사용하여 추정을 수행함
• Linear Regression의 Loss Function은 Closed Form Quadratic 이기 때문에 미분만으로 쉽게 추정 가능
• 𝜷 가 여러 개 일 때 똑같이 각 𝜷 에 대해 미분 수행 후 추정함
  

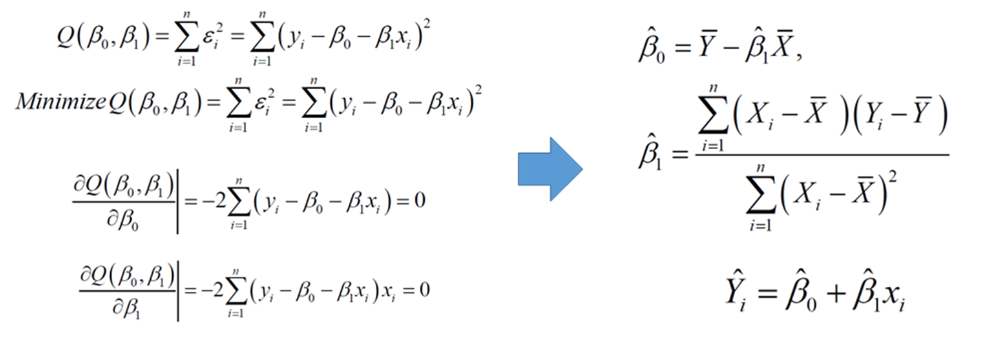
β 계수와 p-value의 해석

• 𝜷 에 대한 p-value가 낮으면 기울기가 0 이 아닌 것으로 판명
• 통상적으로 p-value가 0.05이하면 의미 있다고 판단 ( 𝜷 의 기울기가 0일 확률이 0.05 이하라고 해석함)
• 즉, p-value가 0.05 이하면 $𝑯_𝟎$(귀무가설)은 기각 되며 $𝑯_𝟏$ (대립가설)이 채택 됨
  

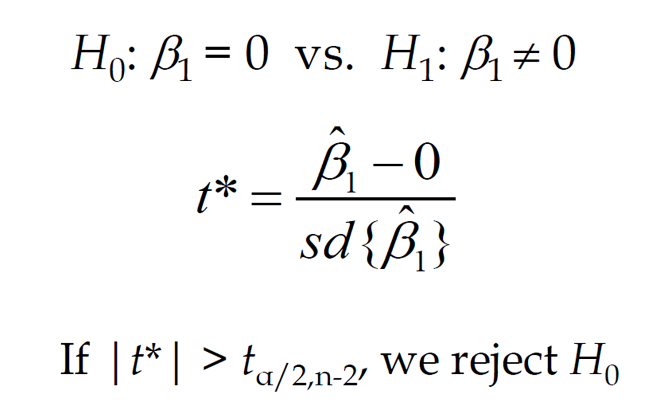
2가지 Factor를 활용한 Model의 Output 해석

Factor 1: $\beta_i$ ($\beta_0$ 제외)

• X가 1단위 증가 시 Y에 영향을 미치는 정도
  • $\beta_1$ 이 10인 경우 $X_1$이 1 증가했을 때 Y에 10의 영향을 미침
• $\beta_i$ 값이 크면 Y에 영향을 크게 미친다고 판단할 수 있음
• 하지만, X간 Scale이 다를 수 있기 때문에 X간 상대적인 비교는 불가함
  • 키와 몸무게는 기본적으로 Scale이 다름

Factor 2: p-value

• $\beta_i$ 값이 크지만 p-value 값이 높으면 의미가 없음

따라서, $\beta_i$ 값과 p-value 값, 두 가지 조건이 맞아야 유의미 하다고 판단할 수 있음