PRM 알고리즘

두부김치·2024년 4월 13일

Path Planning

로봇경로계획

목록 보기

11/17

1. PRM 알고리즘 개요

1996년 Kavraki 등에 의해 제안된 샘플링 경로 계획 방법
지도 전역에서 무작위로 샘플을 추출하고, 샘플들을 연결하여 지도 전역에 대한 로드맵을 생성
생성된 로드맵에 시작 지점과 도착 지점을 추가하여, 두 점을 연결하는 경로를 탐색
시작과 도착 지점이 변경되더라도, 생성된 로드맵을 재활용 가능
2단계로 구성
- 로드맵 구성 단계
- 경로 탐색 단계(쿼리 단계)

2. PRM 알고리즘 단계

1. 로드맵 구성 단계

로드맵 구성 단계의 Pseudo Code

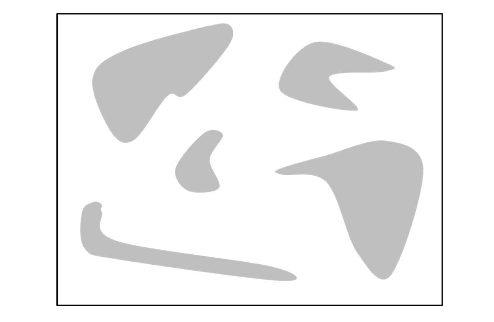
초기화

주어진 지도에서 노드(V) 및 간선(E)등을 초기화
흰색 영역 : 이동 가능한 영역
회색 영역 : 이동 불가능한 영역(예: 장애물 등)

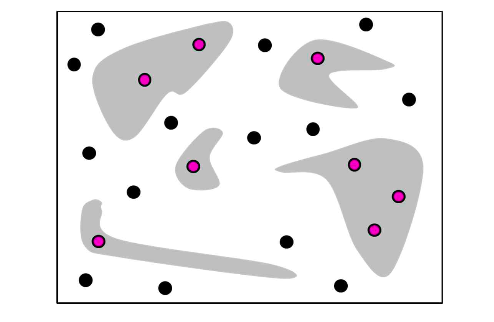
Sample Free

주어진 지도에서 무작위로 샘플을 추출
- 검정색 노드 : 이동 가능한 노드
- 분홍색 노드 : 이동할 수 없는 영역에 위치한 노드

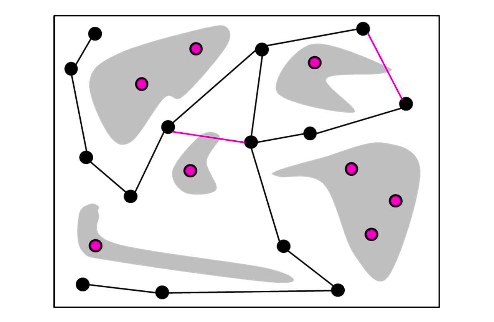
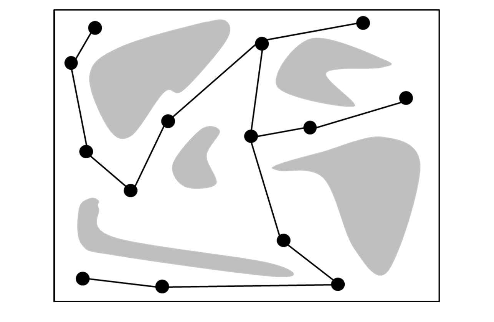
Connecting Nodes

일정한 반경 내의 노드를 간선으로 연결

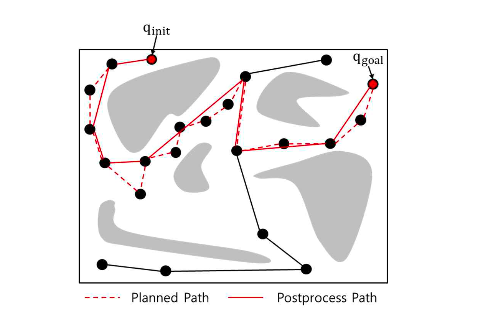
Generate Roadmap

장애물 충돌 등으로 인하여 제외되는 노드 및 간선 등을 제외하고 로드맵을 완성

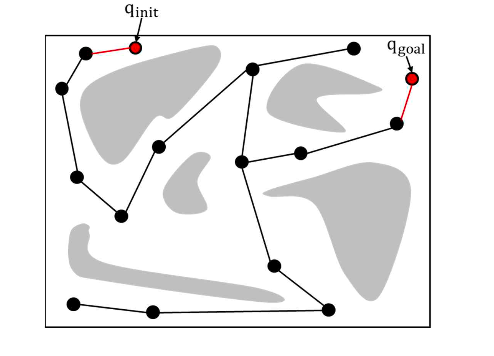
2. 경로 계획 단계

Query Configure

로드맵에, 시작 노드와 도착 노드를 추가

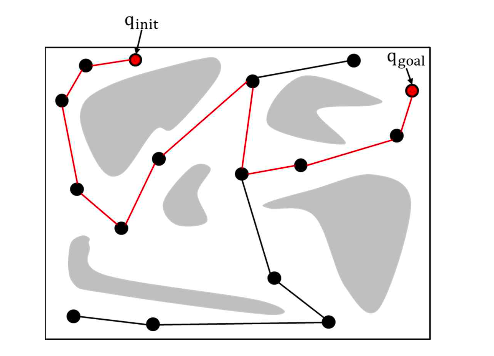
Path Planning

시작 노드에서 도착 노드까지의 최단 경로를 탐색

3. PRM 실습 코드

# numpy와 networkx, matplotlib의 pyplot 모듈을 임포트합니다.
import numpy as np
import networkx as nx
import matplotlib.pyplot as plt
# scipy에서 유클리드 거리를 계산하기 위한 모듈을 임포트합니다.
from scipy.spatial.distance import euclidean

# 비어 있는 공간에서 장애물을 피하면서 지정된 개수의 샘플을 추출하는 함수를 정의합니다.
def sample_free_space(space_size, num_samples, obstacles):
    samples = []  # 추출된 샘플을 담을 리스트를 초기화합니다.
    while len(samples) < num_samples:
        # 공간 내에서 임의의 점을 생성합니다. 좌표 범위는 0부터 space_size까지입니다.
        point = np.random.uniform(0, space_size, 2)
        # 생성된 점이 장애물과 충돌하지 않는지 확인합니다.
        if not is_colliding(point, obstacles):
            samples.append(tuple(point))  # 충돌하지 않으면 샘플 리스트에 추가합니다.
    return samples

# 주어진 점이 장애물과 충돌하는지 확인하는 함수를 정의합니다.
def is_colliding(point, obstacles):
    for obs in obstacles:
        # 점과 장애물의 중심 사이의 거리가 장애물의 반지름보다 작으면 충돌로 간주합니다.
        if euclidean(point, obs[0]) < obs[1]:
            return True  # 충돌이 있으면 True를 반환합니다.
    return False

# 두 점을 연결하는 선분과 원형 장애물 사이의 충돌을 확인하는 함수를 정의합니다.
def line_circle_collision(p1, p2, center, radius):
    # p1과 p2를 연결하는 직선의 방향 벡터를 구합니다.
    d = np.array(p2) - np.array(p1)
    f = np.array(p1) - center  # 장애물 중심과 p1의 거리 벡터를 구합니다.

    # 이차 방정식의 계수를 계산합니다.
    a = np.dot(d, d)
    b = 2*np.dot(f, d)
    c = np.dot(f, f) - radius*radius

    discriminant = b*b - 4*a*c  # 판별식을 계산합니다.
    if discriminant < 0:
        return False  # 판별식이 음수면 교점이 없으므로 충돌이 없는 것으로 판단합니다.

    t1 = (-b - np.sqrt(discriminant)) / (2*a)  # 교점의 파라미터 값을 계산합니다.
    t2 = (-b + np.sqrt(discriminant)) / (2*a)

    # 두 교점 중 하나라도 선분 내에 있으면 충돌이 있는 것으로 판단합니다.
    if (t1 >= 0 and t1 < 1) or (t2 >= 0 and t2 <= 1):
        return True
    
    return False

# 두 점을 연결하는 선분과 장애물 사이의 충돌을 확인하는 함수를 정의합니다.
def is_edge_colliding(p1, p2, obstacles):
    for obs in obstacles:
        if line_circle_collision(p1, p2, obs[0], obs[1]):
            return True  # 충돌이 있으면 True를 반환합니다.
    return False

# 생성된 노드들을 최대 거리 내에서 연결하는 함수를 정의합니다.
def connect_nodes(nodes, max_distance, obstacles):
    edges = []  # 생성된 엣지를 담을 리스트를 초기화합니다.
    for i, n1 in enumerate(nodes):
        for n2 in nodes[i+1:]:
            n1_array, n2_array = np.array(n1), np.array(n2)
            # 두 노드 사이의 거리가 최대 거리 이내이고 충돌이 없으면 엣지를 추가합니다.
            if euclidean(n1_array, n2_array) <= max_distance:
                if not is_edge_colliding(n1_array, n2_array, obstacles):
                    edges.append([n1, n2])
    return edges

# PRM(Probabilistic Roadmap) 알고리즘을 실행하는 함수를 정의합니다.
def prm(space_size, num_samples, max_distance, start, goal, obstacles):
    if is_colliding(start, obstacles) or is_colliding(goal, obstacles):
        print("Start or goal position is in collision")  # 시작점이나 목표점이 충돌하면 에러 메시지를 출력합니다.
        return None
    
    start = tuple(start)  # 시작점을 튜플 형태로 변환합니다.
    goal = tuple(goal)    # 목표점을 튜플 형태로 변환합니다.

    # 시작점과 목표점을 포함하여 무작위 샘플을 추출합니다.
    nodes = sample_free_space(space_size, num_samples, obstacles)
    nodes = [start] + nodes + [goal]  # 시작점과 목표점을 추가합니다.
    # 노드들을 최대 거리 내에서 연결하여 엣지를 생성합니다.
    edges = connect_nodes(nodes, max_distance, obstacles)

    # 그래프를 생성하고, 시작점에서 목표점까지의 경로가 있는지 확인합니다.
    graph = nx.Graph()
    graph.add_nodes_from(nodes)
    graph.add_edges_from(edges)

    if nx.has_path(graph, start, goal):
        # 시작점에서 목표점까지의 최단 경로를 찾습니다.
        path = nx.shortest_path(graph, start, goal, weight="distance")
        return path, nodes, edges
    else:
        return None, nodes, edges

# PRM 알고리즘의 결과를 시각화하는 함수를 정의합니다.
def plot_prm(start, goal, space_size, obstacles, nodes, edges, path):
    fig, ax = plt.subplots()
    # 장애물을 그립니다.
    for obs in obstacles:
        circle = plt.Circle(obs[0], obs[1], color="gray", alpha=0.5)
        ax.add_artist(circle)
    # 노드들을 그립니다.
    for node in nodes:
        plt.scatter(*node, c='b', s=10)
    # 엣지를 그립니다.
    for edge in edges:
        plt.plot([edge[0][0], edge[1][0]], [edge[0][1], edge[1][1]], 'k-', lw=0.5)

    # 시작점과 목표점을 그립니다.
    ax.plot(start[0], start[1], 'bo', markersize=10, label="Start")
    ax.plot(goal[0], goal[1], 'mo', markersize=10, label="Target")

    if path:
        # 경로를 그립니다.
        plt.plot(*zip(*path), 'go-', lw=2)

    # 그래프의 범위를 설정합니다.
    plt.xlim(0, space_size)
    plt.ylim(0, space_size)
    plt.legend()
    plt.show()

if __name__ == "__main__":
    space_size = 100  # 공간의 크기를 설정합니다.
    num_samples = 100  # 샘플의 개수를 설정합니다.
    max_distance = 20  # 최대 거리를 설정합니다.
    start = np.array([5,5])  # 시작점을 설정합니다.
    goal = np.array([95, 95])  # 목표점을 설정합니다.
    obstacles = [(np.array([50, 50]), 10), (np.array([30,70]), 5), (np.array([70, 30]), 5)]  # 장애물을 설정합니다.

    # PRM 알고리즘을 실행하고 결과를 받습니다.
    path, nodes, edges = prm(space_size, num_samples, max_distance, start, goal, obstacles)

    if path:
        print("Path found:", path)  # 경로가 있으면 경로를 출력합니다.
        # 결과를 시각화합니다.
        plot_prm(start, goal, space_size, obstacles, nodes, edges, path)
    else:
        print("No path found")  # 경로가 없으면 에러 메시지를 출력합니다.

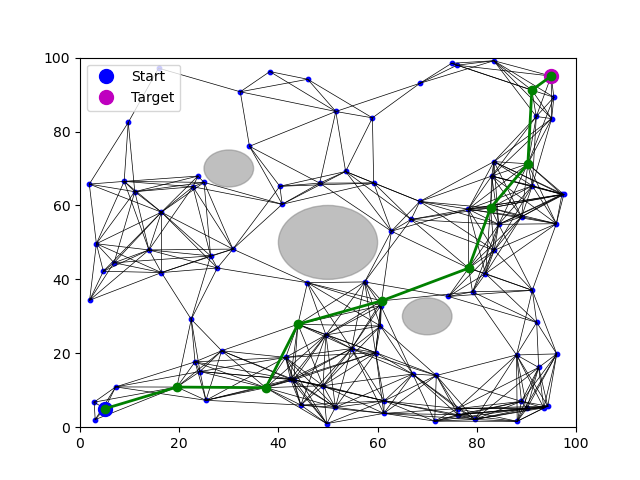
4. PRM 알고리즘 고려사항

샘플링 방법

균등(Uniform)랜덤 샘플링은 구현하기 쉽고, 무난한 방법 중 하나
- 한계: 좁은 통로가 있는 경우, 통로의 좁은 영역에서 샘플을 선택해야만 적절한 로드맵을 생성하여 경로를 탐색할 수 있음
- 다양한 샘플링 방법에 대한 연구
  - 장애물 충돌 시 방향성을 고려
  - 가우시안 분포 등 이용