[Algorithm] 정렬 : Merge Sort

이번엔 merge sort 알고리즘에 대해서 알아본다.

Merge Sort

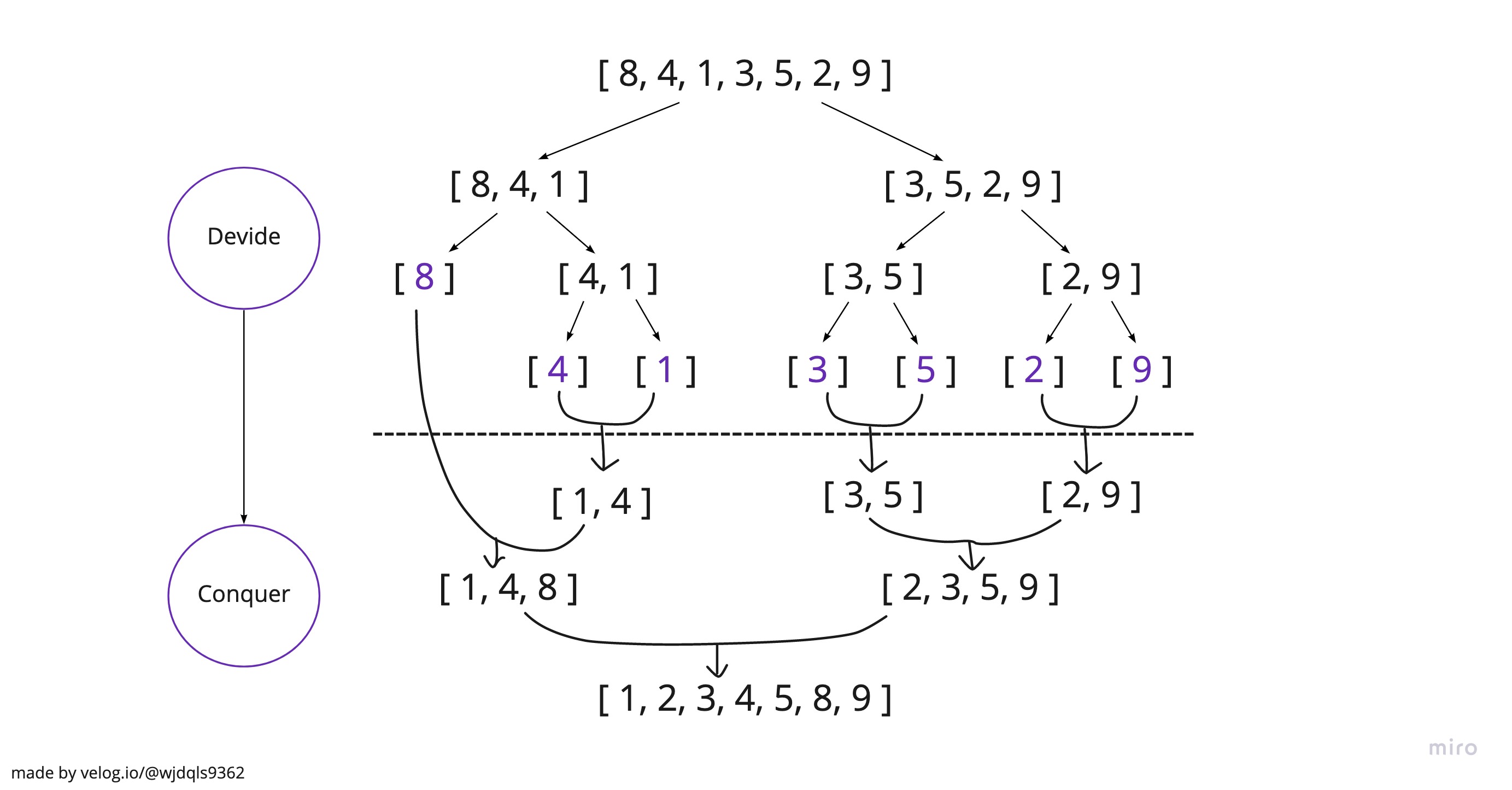
Merge Sort(병합 정렬)는 Quick Sort와 같이 Devide-Conquer 방식을 이용한 알고리즘이다. O(Nlog2N)의 시간복잡도를 가진다.

알고리즘의 플로우는 위와 같다.

1. N의 길이를 가진 배열 리스트를 1의 길이를 가진 '부분 리스트'가 N개 모인 것으로 취급한다.
2. 인접한 부분 리스트들을 정렬하여 2의 길이를 가진 부분 리스트로 병합한다.
3. 2의 길이를 가진 부분 리스트들을 4의 길이를 가진 부분 리스트로 합친다.
4. 하나의 정렬된 리스트가 될 때까지 위 과정을 반복한다.

단점

이러한 합병 정렬은 데이터가 배열인 경우 새로운 임시 배열을 구성하기 때문에 제자리 정렬이 불가하다. 그런 경우 데이터의 크기가 매우 큰 경우 요소의 이동 횟수가 많아져 시간낭비를 할 수 있다.

장점

그러나, 데이터가 Linked-list(연결 리스트)로 구성된 경우에는 리스트의 인덱스만 변경하며 구현하므로 제자리 정렬이 가능해진다. 이 경우에 데이터가 매우 큰 경우라면 합병 정렬이나 퀵 정렬보다 더 효율적이라고 한다.

// conquer 단계 시 인접 배열 요소 정렬 합병 함수
function merge(left, right) {
  let merged = [];
  let leftInx = 0, rightIdx = 0;
  const size = left.length + right.length;
  
  for (let i = 0; i < size; i += 1) { // 인근 배열 합친 길이 만큼만 반복
    if (leftIdx가 left.length 이상일 경우) { // left 요소가 전부 push된 상태
      // merged에 현재 rightIdx 요소를 push하고 rightIdx++;
    } else if (rightIdx가 right.length 인 경우(right요소가 전부 push된 상태) || 현재 leftIdx 요소가 rightIdx 요소보다 같거나 작은 경우) {
      // merged에 현재 leftIdx 요소를 push하고 leftIdx++;
    } else { // 현재 rightIdx 요소가 leftIdx 요소보다 같거나 작은 경우
      // merged에 현재 rightIdx 요소를 push하고 rightIdx++;
    }
  }
  return merged;
};

// 병합정렬 함수 : 재귀를 이용해 구현
function mergeSort(arr) {
  // 탈출 조건
  if (arr.length < 2) return arr;
  
  const middle = parseInt(arr.length / 2); // parseInt : 문자열 혹은 숫자를 2번째 인자의 진법으로 변환하는 함수(기본값은 10진법)
  const left = mergeSort(arr.slice(0, middle));
  const right = mergeSort(arr.slice(middle));
  const merged = merge(left, right);
  
  return merged;
};