Extension to Block-Fading Channels

통신 분야에 ML 알고리즘을 적용하는 것과 관련된 대부분의 어려운 점은, 내재된 모델을 학습하기 위해 DNNs를 이용할 때 network가 학습 과정에서와 거의 동일한 통계적 관계 하에서 작동되어야 한다는 점에서 비롯된다. 무선 통신 channel은 본질적으로 dynamic 하기 때문에 보통 block-fading으로 모델링 되는데, 그러한 channel에서는 각각의 transmitted block이 서로 다른 통계적 변환을 겪을 수 있다.

따라서 block-fading channel에서 ViterbiNet을 사용하기 위한 방법으로 매우 다양한 channel들로부터 sample을 얻어 학습하는 것을 생각해볼 수 있다. 하지만 이런 방식은 다양한 channel 조건을 다루기 위한 학습 data를 너무 많이 필요로 하고, 만약 학습한 channel과 시험을 위한 channel 모델이 다르면 network 성능이 크게 떨어질 수도 있다는 단점이 있다.

이에 저자는 receiver로 하여금 디지털 통신 신호, 특히 coded communication 고유의 structure를 이용하여 time-varying channel의 condition을 추적 및 조정할 수 있도록 함으로써 ViterbiNet을 확장했다. 이어지는 subsection에서는 먼저 coded communication과 block-fading channel을 고려하여 channel model을 확장해보고, ViterbiNet이 실시간 training을 위해 channel coding을 어떤 식으로 사용하는지 알아볼 것이다.

Coded Communications over Block-Fading Channels

Coded communication에서 $t$ 개의 송신 channel symbol들로 이루어진 각각의 block은 $b$ bits의 channel codeword를 나타낸다. 그 중 $j \in \mathcal{N}$ 번째 block을 생각해보면 bits에 대한 vector $\mathbf{B}^b_{(j)} \in \{ 0, 1 \}^b$ 는 차례로 encoding, modulation을 거쳐 symbol vector $\mathbf{S}^t_{(j)}$ 가 되고, 이후 channel을 거쳐 송신된다.

위와 같은 channel coding의 목적은 receiver에서 information bits의 복원을 용인하게 만들기 위함인데, channel code는 Reed-Solomon (RS) codes와 같은 FEC codes와 checksums, cyclic redundancy checks와 같은 error detections codes로 구성될 수 있다.

Receiver는 information bits $\hat{\mathbf{B}}^b_{(j)} \in \{ 0, 1 \}^b$ 를 decode 하기 위해 복원한 symbols $\hat{\mathbf{S}}^t_{(j)}$ 를 사용한다. 이때 FEC codes는 몇몇 symbol의 복원이 정확히 안 되더라도 $(\mathbf{S}^t_{(j)} \neq \hat{\mathbf{S}}^t_{(j)})$, information bits가 완벽히 decoding 될 수 있도록 해준다. 또한 error detection codes는 receiver에서 information bits가 정확히 복원되었는지 감지하고, bit error의 개수를 추정할 수 있게 해준다. (이는 $\mathbf{B}^b_{(j)}$ 와 $\hat{\mathbf{B}}^b_{(j)}$ 사이의 Hamming distance를 의미하고, $\epsilon_{(j)}$와 같이 표기한다.)

Block-fading channel 상황에서, 송신한 channel symbols로 구성된 각각의 block은 서로 다른 channel을 겪는다. 특히 $j \in \mathcal{N}$ 번째 block에 대해 생각해보면, input $\mathbf{S}^t_{(j)}$가 주어졌을 때의 channel output $\mathbf{Y}^t_{(j)}$ 분포는 finite-memory causal stationary channel을 나타낸다. 하지만 이러한 조건부 확률 분포는 서로 다른 block들 사이에서 달라질 수 있으니, block index $j$에 의존한다고 볼 수 있다. Fig 1 은 이러한 channel model을 나타낸 diagram 이다.

Fig 1. Coded communications over block-fading channels

정리하면 각 block은 서로 다른 channel input-output 관계를 겪기 때문에, receiver는 performance의 최적화를 위해 varying channel condition을 잘 추적하고 그에 적응할 수 있어야 한다. 다음 subsection에서는 ViterbiNet이 상대적으로 적은 training sets을 필요로 한다는 사실이 어떻게 coded communications가 존재한다는 것과 연결되어, receiver로 하여금 channel의 variation을 실시간으로 추적할 수 있게 하는지에 대해 알아보자.

ViterbiNet with Online Training

ViterbiNet은 single block에 대한 channel outputs $\mathbf{Y}^t_{(j)}$을 사용하여 transmitted symbols의 추정값 $\hat{\mathbf{S}}^t_{(j)}$를 만든다. (이때 $j \in \mathcal{N}$은 block index를 의미한다.)

FEC codes가 있는 한, code의 minimal distance 보다 detection error의 개수가 크지 않다면 encoding 된 bit는 완벽하게 복원될 수 있다. 따라서 FEC code가 그러한 error를 보상할 수 있을만큼 ViterbiNet의 symbol error rate (SER)이 충분히 작다면 전송된 message는 복원될 수 있다. 복원된 message는 새로운 training samples $\tilde{\mathbf{S}}^t_{(j)}$를 생성하기 위해 re-encoded 될 수도 있는데, 이를 meta-training 이라 한다. 만약 encoding 된 bits가 성공적으로 복원되었다면, $\tilde{\mathbf{S}}^t_{(j)}$는 $\mathbf{Y}^t_{(j)}$이 얻어질 때의 실제 channel input을 나타낸다. 정리하면 $\tilde{\mathbf{S}}^t_{(j)}$ 와 $\mathbf{Y}^t_{(j)}$의 pair는 ViterbiNet을 re-train 하는 데 사용될 수 있다.

ViterbiNet의 간단한 DNN 구조는, block-fading channel에서의 단일 전송 블록의 사이즈와 같이 상대적으로 적은 수의 training samples를 이용하여 빠르고 효율적으로 network를 재학습 시킬 수 있음을 암시한다. 논문에서 제안하는 실시간 training mechanism은 Fig 2 와 같다.

Fig 2. Online training model

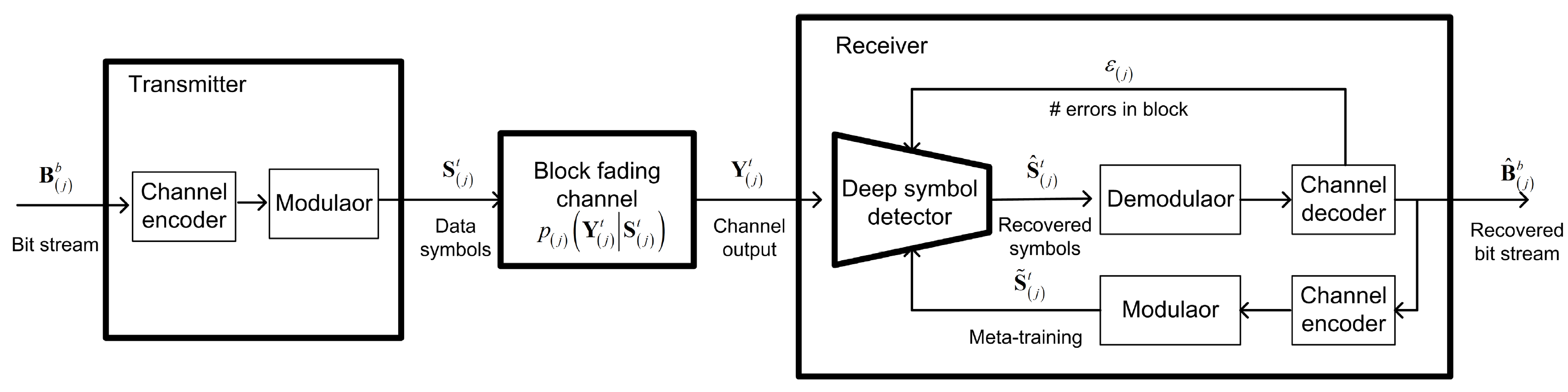
Decision-directed 방식의 근본적인 drawback은 decision error에 민감하다는 것이다. 예를 들어 FEC decoder가 encoded bits를 성공적으로 복원하지 못하면, meta-training samples $\tilde{\mathbf{S}}^t_{(j)}$는 $\mathbf{Y}^t_{(j)}$의 결과를 내는 channel input을 정확하게 표현할 수 없다. 그렇다면 특히 decoding error가 자주 발생하는 low SNR 상황에서 부정확한 training sequence로 인해, re-trained ViterbiNet의 복원 정확도가 매우 안 좋을 것이다.

하지만 FEC codes에 error detection codes가 더해진다면, decision error의 영향은 약화될 것이다. Receiver가 $j$ 번째 block을 decoding 하는 과정에서의 bit error 개수인 $\epsilon_{(j)}$에 대한 추정값을 잘 가지고 있다고 생각해보자. 그렇다면 receiver는 어떠한 threshold $\bar{\epsilon}$ 보다 error의 개수가 작거나 같을 때만 meta-training을 통해 symbol detector를 재학습 하도록 결정할 수 있다. 이러면 정확한 meta-training만 사용될 것이고 decision error의 효과는 작게 조절될 수 있을 것이다. 정리하면, 제안한 online training mechanism은 Algorithm 2 와 같이 요약할 수 있다.

Algorithm 2. Online training of ViterbiNet

• Step 6: Learning rate 설정
  $\Rightarrow$ Expected channel variations 크기에 기반하여 설정돼야 한다.
  Learning rate 값은 이전 channel realizations에 해당하는 과거 학습 set을 바탕으로 조정된 초기 DNN weights와 현재 channel을 나타내는 (일반적으로 훨씬 작은) meta-training set 사이의 기여도를 조절한다. 큰 learning rate를 사용하면 network가 굵직한 channel variations에 잘 적응할 수 있지만, decision error에 대한 알고리즘의 민감도 역시 커질 수 있어서 작은 threshold $\bar{\epsilon}$ 와 함께 사용되어야 한다.

$\bar{\epsilon}$ 의 영향

• If $\bar{\epsilon} = 0$, ViterbiNet을 재학습 시키는 데 사용하는 meta-training symbols가 정확하다는 것을 보장함.
  $\Rightarrow$ 이러한 setting은 적절한 channel variations를 추적하는 능력을 제한시킴.
• $\bar{\epsilon}$ 이 충분히 큰 상황도 고려해야 함.
  $\Rightarrow$ 몇몇 코드의 경우 적은 수의 error로 bit stream을 encoding 하면 전송한 것에 비해 먼 codeword가 발생하여, 부정확한 meta-training labels를 생성할 수 있다.
  정리하면, $\bar{\epsilon}$ 은 block-fading channels를 reliable 하게 추적하는 ViterbiNet의 능력을 결정한다.

마지막으로, 제안한 방법은 meta-training을 생성하기 위해 오직 channel codes에만 집중하는데 이는 추후 digital communication signals의 다양한 구조를 이용하도록 확장될 수도 있을 것이다.

Numerical Study

실험은 아래와 같은 조건에서 진행되었다.

• Channel memory $l$ is a-priori known.
• Structure of FC network: $1 \times 100$ layer + Sigmoid + $100 \times 50$ layer + ReLU + $50 \times 16(=\vert m \vert^l)$ layer.
• Mixture model estimator: EM-based fitting
• 5,000 training samples with Adam optimizer
• Cross-entropy loss and learning rate 0.01, 100 epochs, mini-batch size 27 (observations)

자세한 실험 결과는 논문을 참조하자. 본 포스팅에서는 channel을 어떻게 구현하여 simulation 했는지 까지만 다뤄볼 예정이다.

Time-invariant channels

두 가지 finite-memory causal scalar channels에 대해 고려했다. Memory length는 두 경우에 대해 모두 $l=4$ 이다.

ISI channel with AWGN

이때 input-output 관계는 다음과 같이 표현된다.

위 식에서 $\rho>0$는 SNR, $W[i]$는 zero-mean unit variance AWGN, $\mathbf{h}(\gamma) \in \mathcal{R}^l$은 channel vector를 의미한다.
(Exponentially decaying profile $(\mathbf{h})_{\tau} \triangleq e^{-\gamma(\tau-1)}, \textrm{ for } \gamma >0$ )

ISI의 영향은 $\gamma$ 가 커짐에 따라 덜 중요해지지만, 본 simulation 에서는 모든 $\gamma$ 값에 대한 memory length를 4로 고정했다. Channel의 input은 BPSK constellation을 따라 random 하게 결정된다. 즉, $\mathcal{S} = \{ -1, 1 \}$.

Poisson channel

Poisson channel의 경우 channel input은 on-off keying 즉, $\mathcal{S} = \{ 0, 1 \}$ 을 의미한다. Channel output $Y[i]$는 다음 식에 따라 생성된다.

이때 $\mathbb{P}(\lambda)$ 는 Poisson distribution을 의미한다. $(\lambda >0)$

Block-fading channels

본 simulation에서도 위와 같이 두 block-fading channel (ISI with AWGN & Poisson)을 고려했다. 각 송신 block에 대해, 저자는 바로 위에서 소개한 두 channel 식을 각각 따르는 channel model을 사용했고 exponential decay parameter $\gamma$ 는 0.2로 고정했다.

Block에 따라 바뀌는 channel coefficient vector $\mathbf{h}$는 $j$ 번째 block에 대해 아래와 같이 적용된다.
$($여기서 $\mathbf{p}=[51, 39, 33, 21]^\intercal$ 를 사용했다.$)$

Reference

Shlezinger, Nir, et al. "ViterbiNet: A deep learning based Viterbi algorithm for symbol detection." IEEE Transactions on Wireless Communications 19.5 (2020): 3319-3331.