• Paper: RoFormer: Enhanced Transformer with Rotary Position Embedding
• 위 논문은 RoPE 를 제안한 논문이지만, 이후 EleutherAI 에서 Positional Embeddings 으로 구현하여 사용하면서 더 유명해짐
  • GPT-J, GPT-NEO, LLaMA
  • 많은 추가적인 실험을 EleutherAI 에서 진행 및
• https://www.slideshare.net/taeseonryu/roformer-enhanced-transformer-with-rotary-position-embedding 슬라이드의 내용을 많이 참고하였습니다. 감사합니다.

1. Positional Embeddings

1.1 Absolute Positional Embeddings

• 각각의 token x 에 d-dimensional vector p 를 더하는 형태
• Trainable vector 를 쓰는 경우도 있고 (BERT 등), Sinusoid function 을 사용하는 경우도 있음 (Transformer 등)

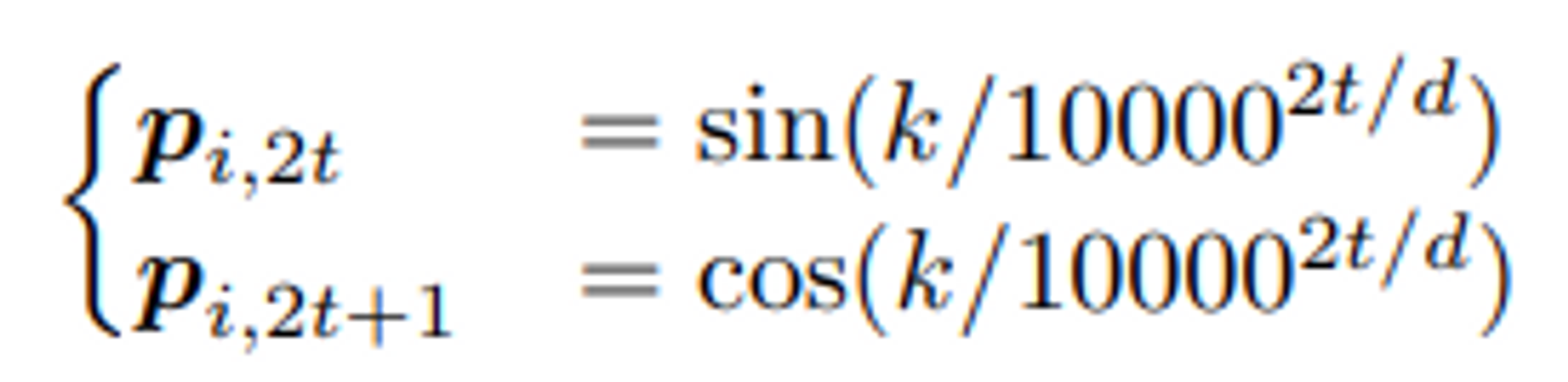
1.2 Relative Positional Embeddings

• Position m 과 n 사이의 relative distance 를 정의
  • 아래 수식의 가정은 특정 거리를 넘어가는 정보는 useful 하지 않다는 것 -> Clipping
  • T5 같은 경우에는 clip 하여 같은 값으로 두는 것이 아닌, 최대 offset 까지 log-scale 로 값을 증가시킴
    $r=clip(m - n, r_{min}, r_{max})$
• Key, Query, Value 에 대하여, 아래와 같이 trainable positional embeddings 를 정의
  • Query 와 Key 의 inner product 시 relative positional 정보를 반영하여 model 에 적용

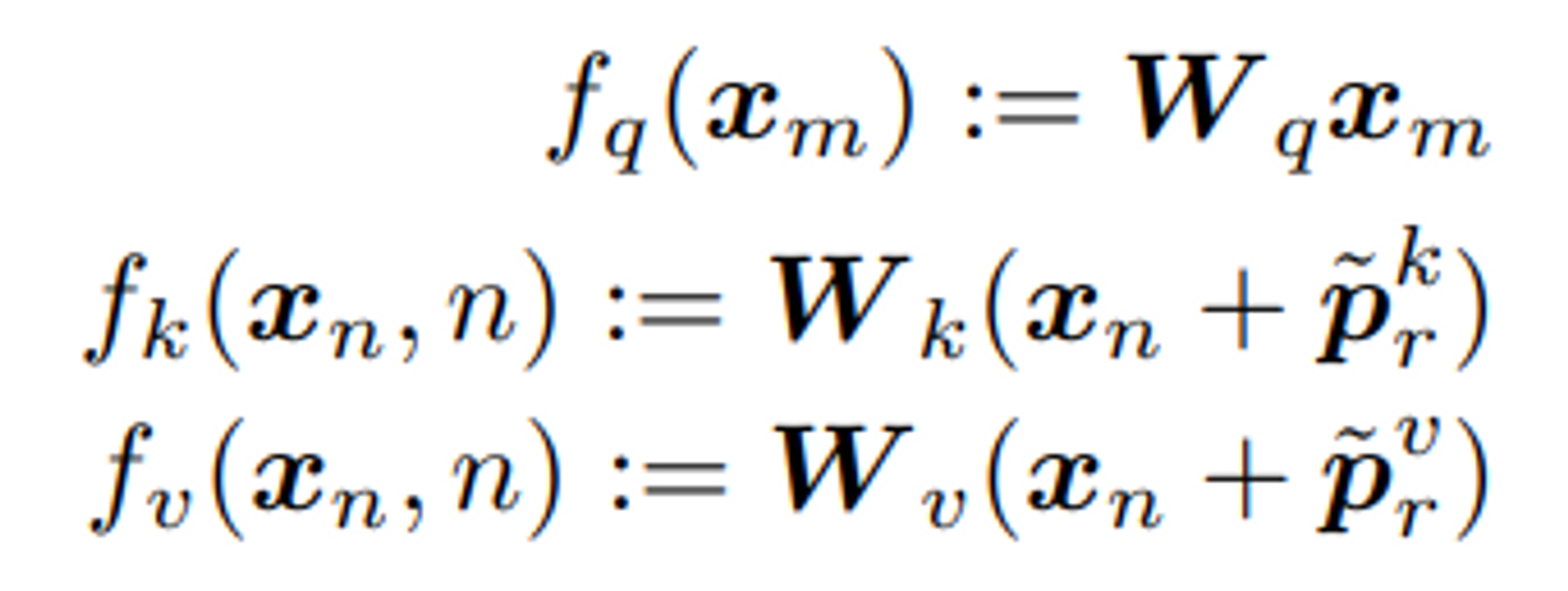
• Inner product 한 결과는 아래와 같고, 이것이 다양한 relative positional embeddings 의 general form 형태라고 볼 수 있음
  • Transformer-XL 에서는 아래 수식을 차례대로 Content-to-Content, Content-to-Position, Position-to-Content, Position-to-Position 으로 해석함

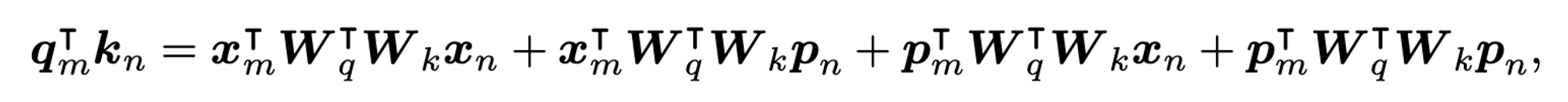
• 다양한 모델에서 사용한 Relative Positional Embeddings 형태
  • Transformer-XL
    • Query 에는 별도 Position Encoding 하지 않음
    • Content-to-Content, Content-to-Position + Global Content bias + Global Position bias 로 해석
    • Value 에서는 Position 활용하지 않음
  • DeBERTa
    • Query 에 대한 Position 정보도 중요하다! (단, 여전히 Position-to-Position 항은 의미가 없다)
      • Query 기준에서의 Position 과 Key 기준에서의 Position 은 서로 다른 의미를 갖게됨
    • Attention 계산 시 Content 와 Relative Position 둘 다 반영된 disentangled matrices 를 사용하여 연산

1.3 Rotary Positional Embeddings

• RoPE 는 RPE 기반의 방법이고, Additive form 이 아닌 Multiplicative 기법 + Sinusoid 아이디어를 활용한 방법임

• Formulation: 통합적인 Relative Position Information 을 위하여 Query, Key 의 Inner product, 함수 g 로 정의된 Position Encoding 을 찾고 싶고, $g$ 는 Word Embeddings 과 상대적인 Position m-n 만을 input 으로 가질 수 있도록 정의하고 싶음
  • 즉, Inner product 가 Relative Position Information 을 포함하도록 변형하고자 함

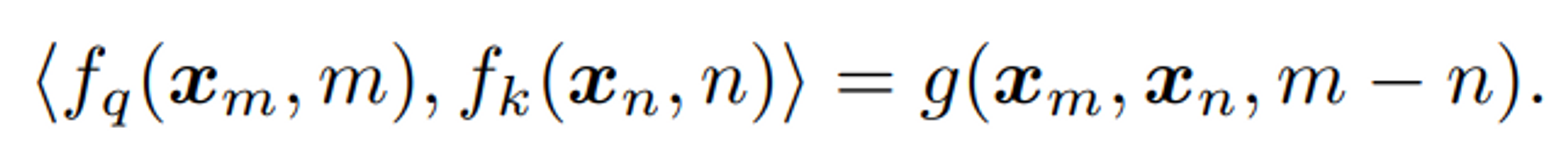
1.3.1 A 2D Case

• 2D Plane 의 Geometric property 를 사용함
  • Token embedding 을 complex form 으로 매핑해보자!
  • Position 정보는 위의 Token embedding 을 rotation 시켜서 표현할 수 있지 않을까?
• 2D 에 대하여 위의 식을 만족하는 $f, g$ 는 아래와 같이 표현됨 (증명 Section 3.4.1)

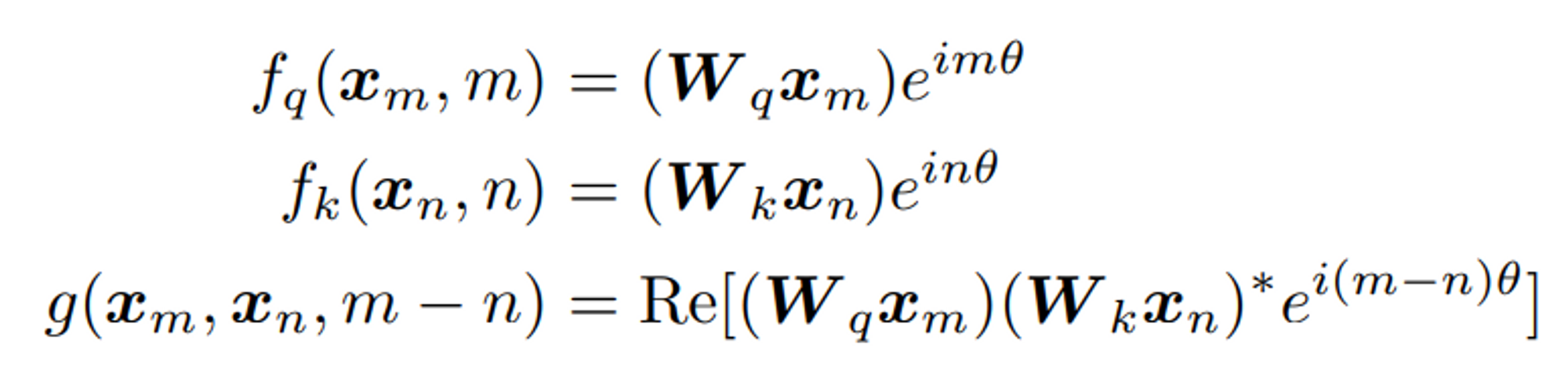
• 다시 말해 $f$ 를 Multiplication Matrix 형태로 바꿔서 써보면,
  • 간단하게 각도 m 배 만큼 회전한 affine-transformed word embedding vector 로 해석할 수 있음
  • 참고: https://en.wikipedia.org/wiki/Rotation_matrix

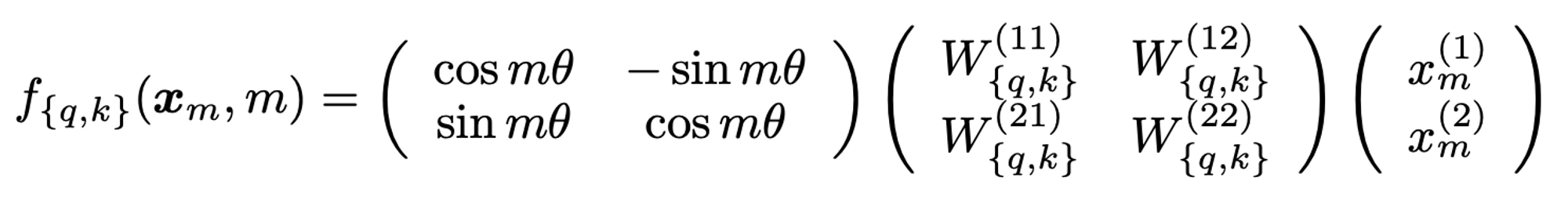
1.3.2 General form

• 2개 dimension 마다 일정한 angle 만큼 회전 시켜서 Position Information 정보를 담음
• 이 때, 세타의 값은 transformer 의 sinusoid 와 같은 매핑 함수를 사용

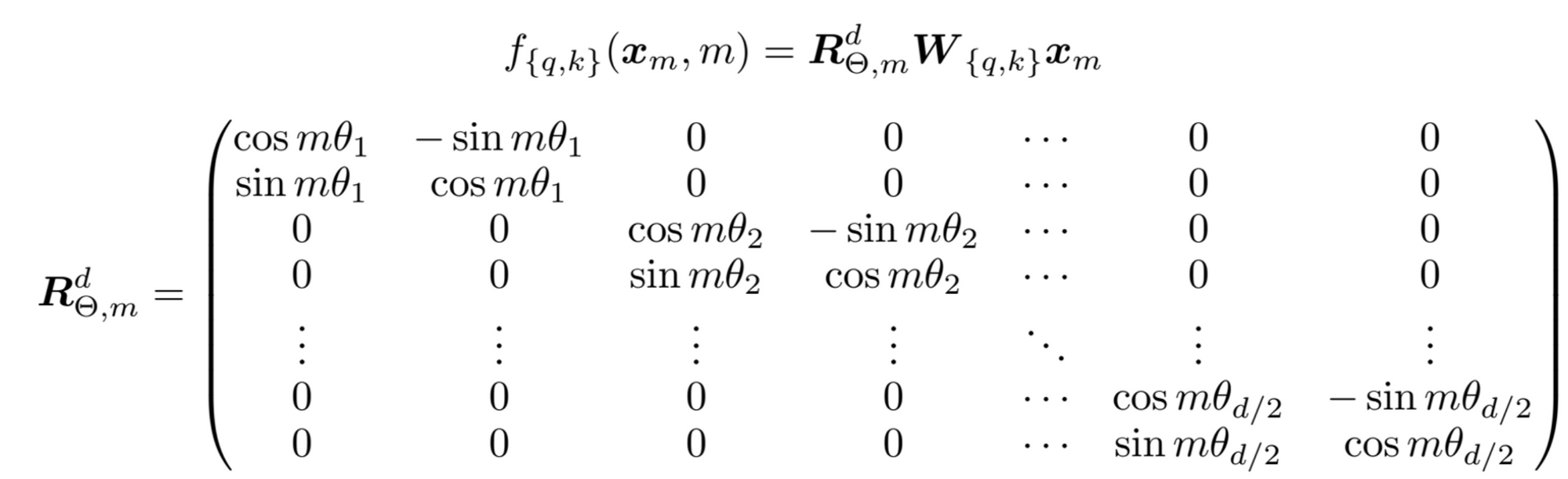
• Inner product 최종 form
  • 위의 (Section 1.2) 의 Relative Position Encoding 과 다르게 Position 정보가 더해지지 않고 곱해진 형태

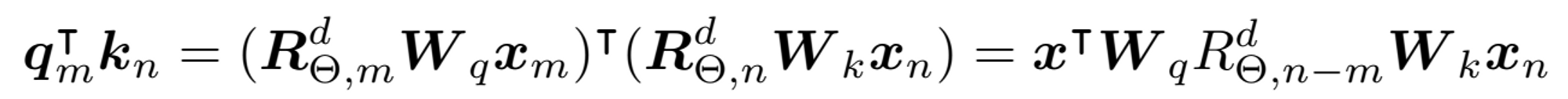
• R matrix
  • R matrix 는 orthogonal matrix 이기 때문에 stability 함
  • Sparse 하기 때문에 위 matrix 를 그대로 연산에 활용하지는 않고, 구현에서는 아래의 형태로 활용함

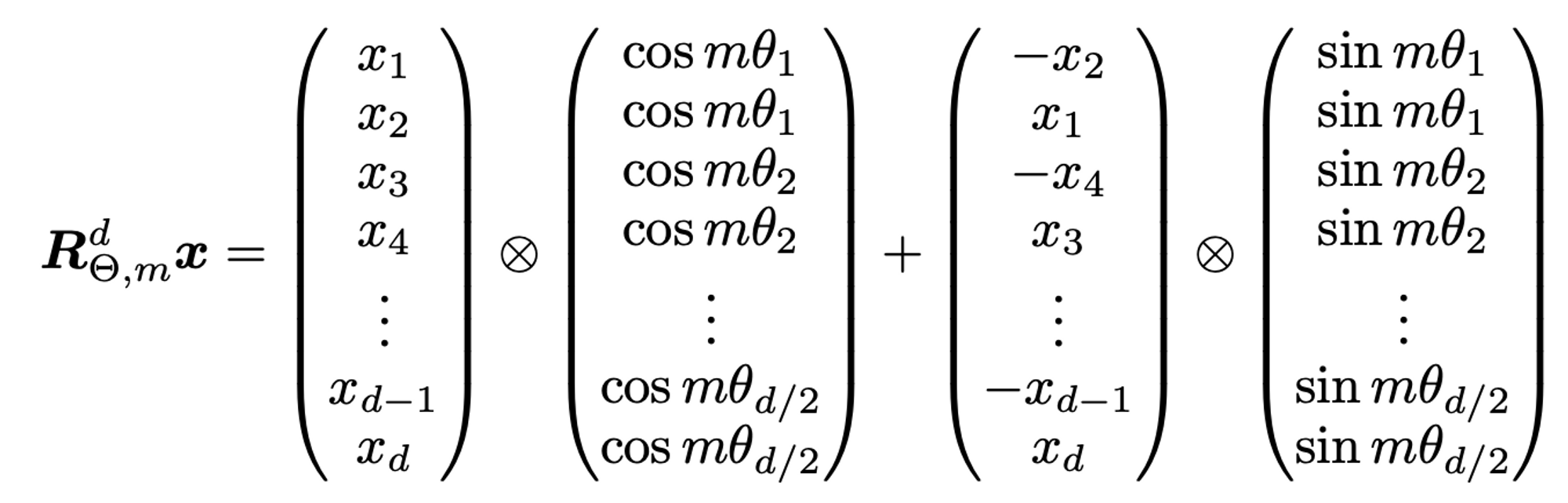
• 그림 설명

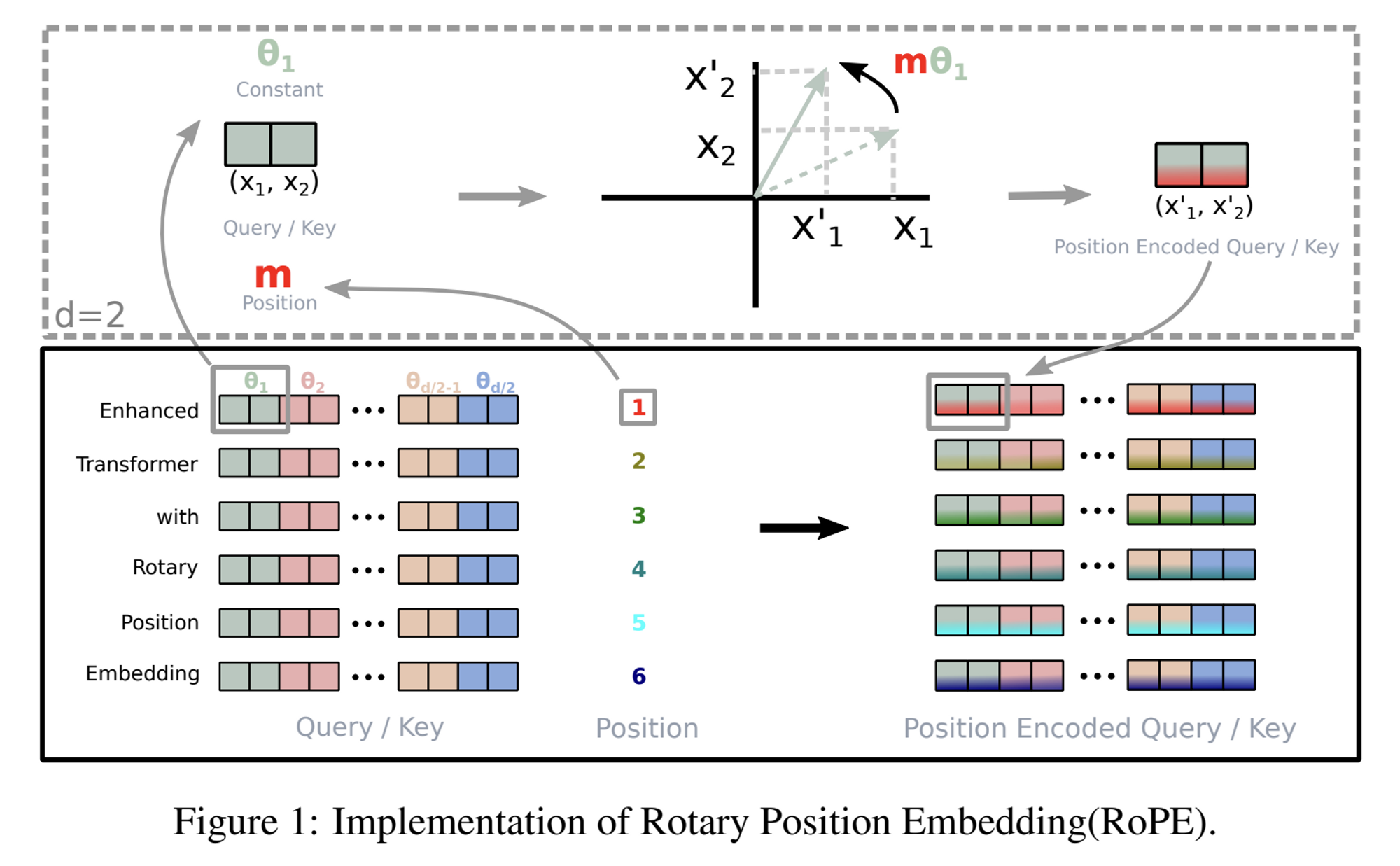
1.3.3 특징

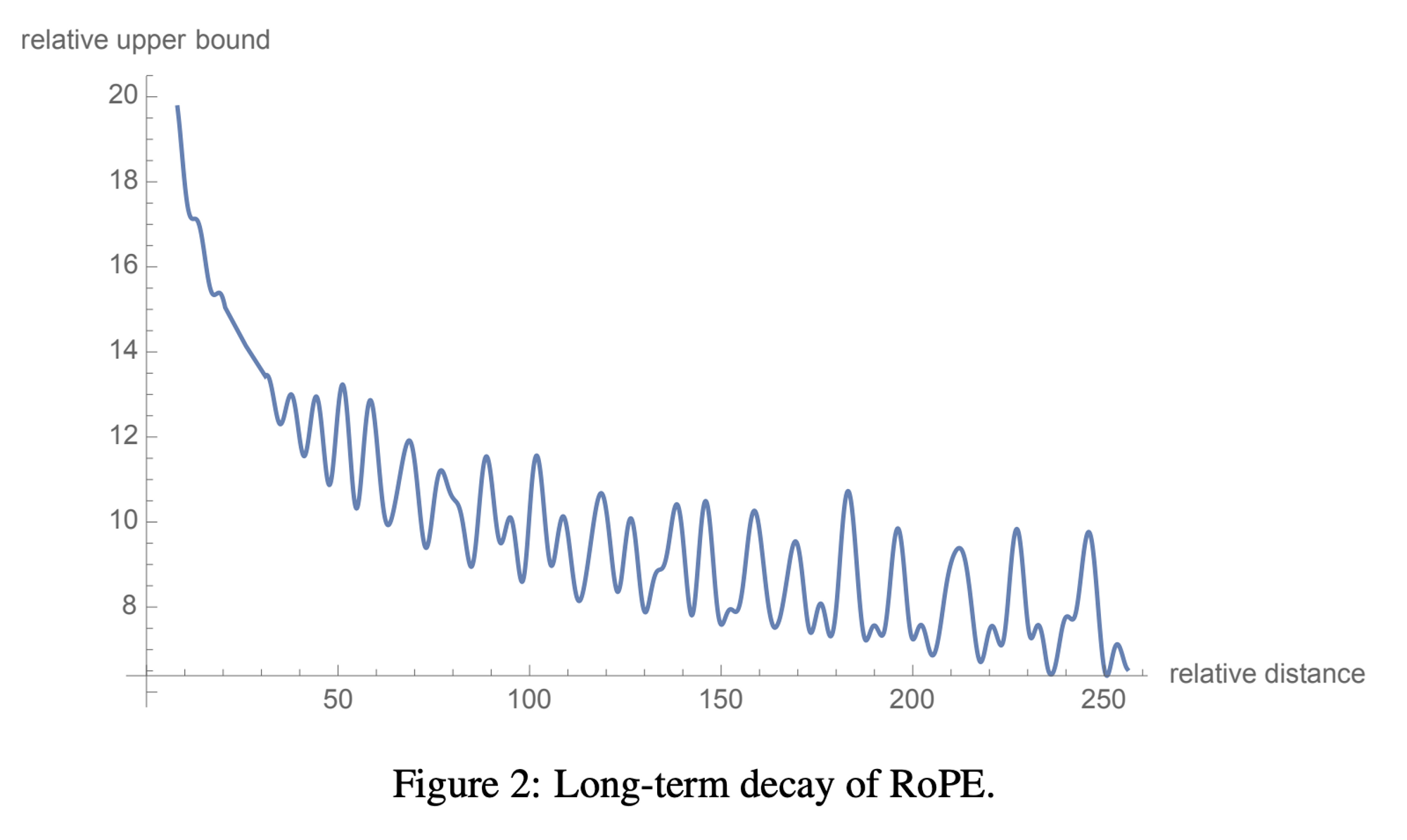
• Long-term decay of RoPE
  • Sinusoid 함수 특징에 의해 Relative Distance 가 커짐에 따라 decay 하게 됨

• Additive 방식에 비하여 Interpretable
• Efficient Transformer 과 조합하기에 적합한 방식이라고 함
  • Full attention matrix 를 필요로 하지 않아서