[백준 c++] 15685 드래곤 커브

문제

https://www.acmicpc.net/problem/15685
N개의 드래곤 커브를 만들었을 때 크기가 1×1인 정사각형의 네 꼭짓점이 모두 드래곤 커브의 일부인 정사각형의 개수를 구하는 문제다.

드래곤 커브는 (시작점 x, 시작점 y, 시작방향 d, 세대 g) 로 입력된다. 입력으로 주어지는 드래곤 커브는 격자 밖으로 벗어나지 않으며 드래곤 커브는 서로 겹칠 수 있다.

방향
0: x좌표가 증가하는 방향 (→)
1: y좌표가 감소하는 방향 (↑)
2: x좌표가 감소하는 방향 (←)
3: y좌표가 증가하는 방향 (↓)

풀이

드래곤 커브 그리기

선분을 그렸을 때 마지막 점을 기준으로 90도 시계방향 회전을 시키는 것이므로
진행방향이 1이었던 선분을 90도 시계방향 회전시킨 선분의 진행방향은 2가 된다.
진행방향이 1,2로 그려진 1세대 드래곤 커브를 2세대로 만들기위해서
마지막 선분부터 진행방향을 대조해서 그리면 2->3, 1->2가 되기때문에 3,2의 진행 방향을 가진 선분을 추가한다.

입력이 4 2 1 3일때
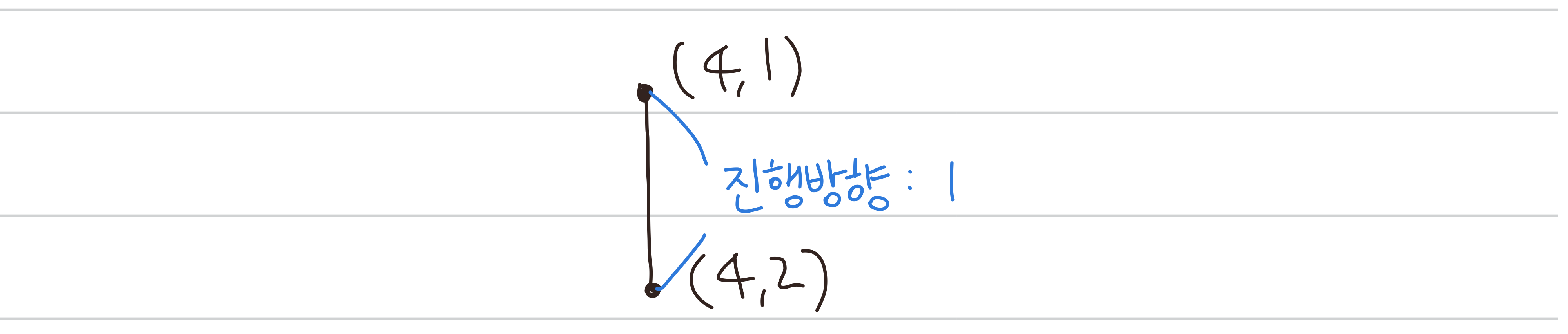
0세대 드래곤 커브의 진행방향: [1]

1세대 드래곤 커브 진행방향: [1][2]

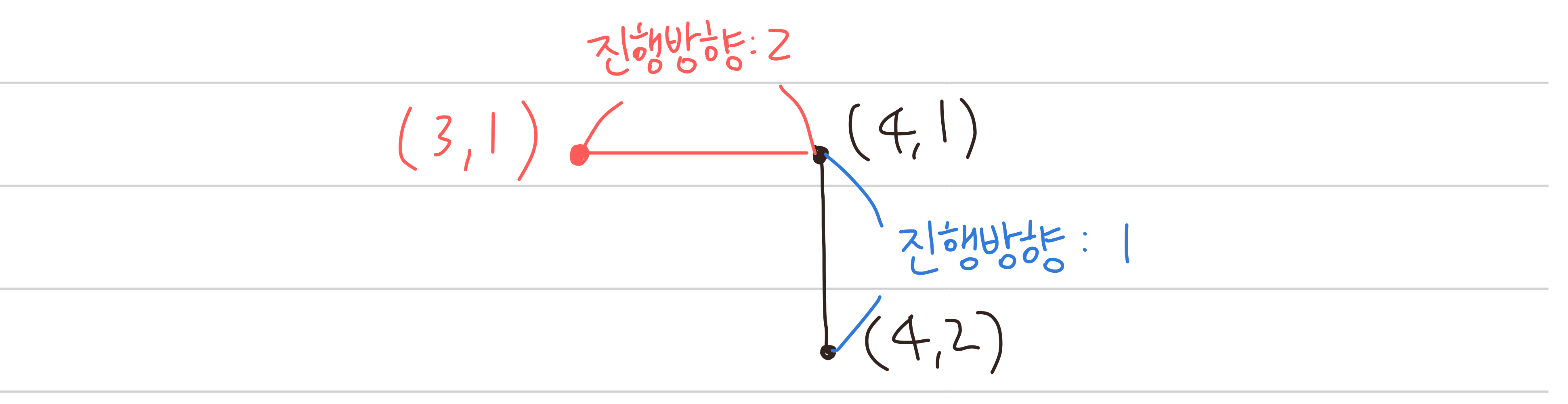
2세대 드래곤 커브 진행방향: [1,2][3,2]

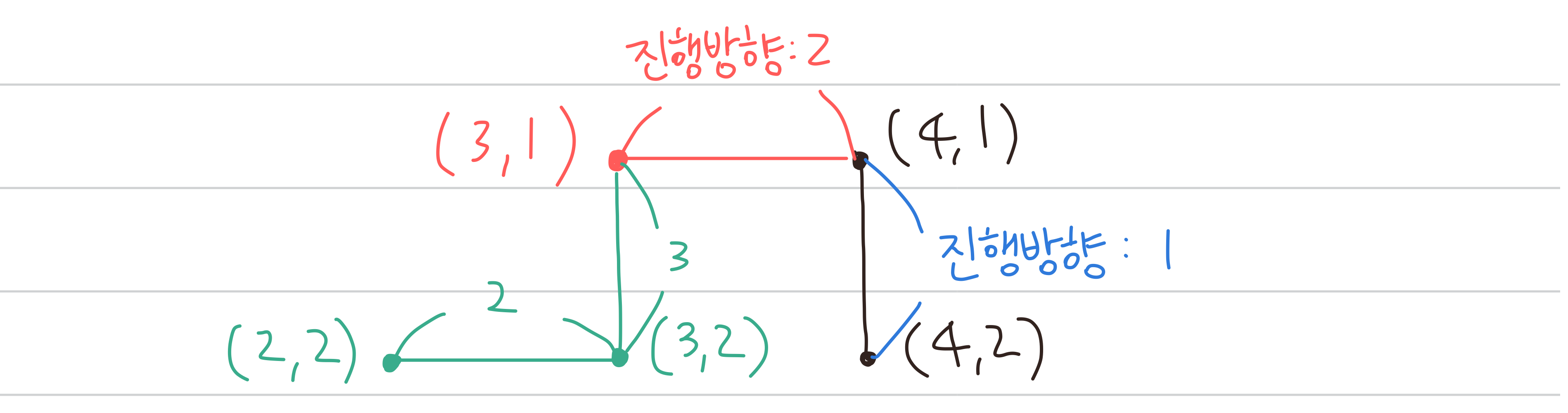
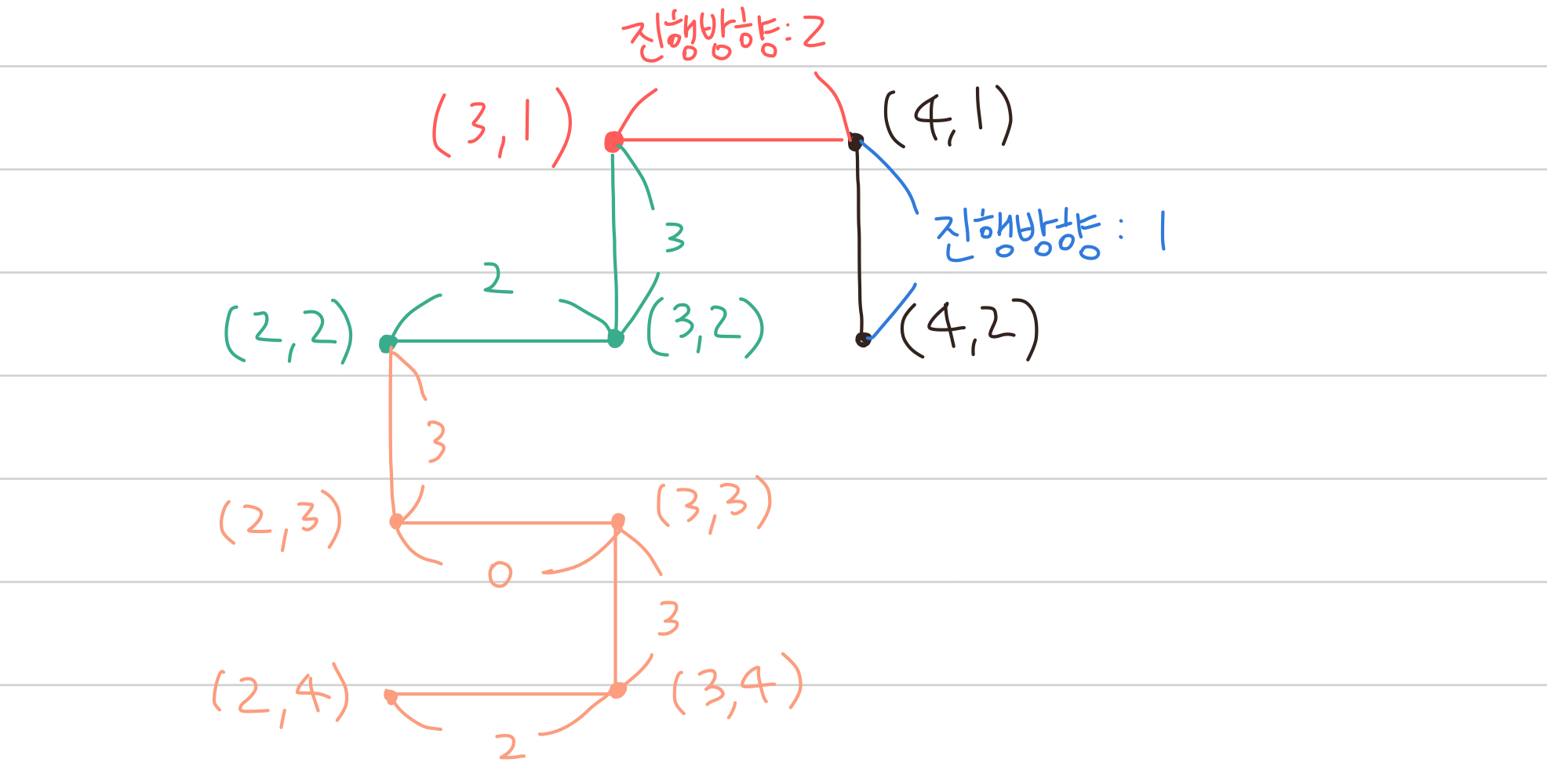
3세대 드래곤 커브 진행방향: [1,2,3,2][3,0,3,2]

int dx[4] = {1, 0, -1, 0}  ->  진행방향에 따른 x좌표 가중치
int dy[4] = {0, -1, 0, 1}  ->  진행방향에 따른 y좌표 가중치

int dir[4] = {1, 2, 3, 0}  ->  현재 진행방향을 idx로 넣었을 때 다음 진행방향 값 

ex) dir[0] = 1 // 현재 진행방향이 0이면 다음 선분의 진행방향은 1이다.

드래곤 커브 정보를 입력받으면 vector에 방향을 집어넣는다.

시작 좌표 a[x][y] = 1
좌표 이동 x += dx[d], y += dy[d]
끝나는 좌표 a[x][y] = 1
여기까지는 0세대 드래곤 커브를 처리한 것이다.

1세대 이상부터는 vector의 size만큼의 선분을 추가로 그려야한다.

v.size()은 최종적으로 g^2이므로 pow(2,g)
vector의 뒤의 원소부터 탐색하며 x,y 값을 바꿔주고 다음 선분의 방향값을 vector에 넣어준다.

정사각형 유무 체크

2중 for문을 통해 드래곤 커브에 포함되는 a[i][j] = 1인 점을 왼쪽 위의 점으로 갖는 1x1크기의 정사각형이 가능한지 체크하고 가능하다면 visited처리를 해준다.

코드

#include <iostream>
#include <algorithm>
#include <vector>
#include <cmath>
using namespace std;
int n, x, y, d, g, res, a[104][104], visited[104][104];
int dx[4] = {1, 0, -1, 0}, dy[4] = {0, -1, 0, 1}, dir[4] = {1, 2, 3, 0};
vector<int> v;
void go(int x, int y, int d, int g)
{
    v.push_back(d);
    a[x][y] = 1;
    x += dx[d], y += dy[d];
    a[x][y] = 1;

    while (v.size() < pow(2, g))
    {
        for (int i = v.size() - 1; i >= 0; i--)
        {
            x += dx[dir[v[i]]], y += dy[dir[v[i]]];
            a[x][y] = 1;
            v.push_back(dir[v[i]]);
        }
    }
    v.clear();
}

void rec(int x, int y)
{
    if (x + 1 > 100 || y + 1 > 100)
        return;
    if (a[x][y + 1] && a[x + 1][y] && a[x + 1][y + 1])
    {
        res++;
        visited[x][y] = 1;
    }
    return;
}

int main()
{
    cin >> n;
    for (int i = 0; i < n; i++)
    {
        cin >> x >> y >> d >> g;
        go(x, y, d, g);
    }
    for (int i = 0; i < 101; i++)
    {
        for (int j = 0; j < 101; j++)
        {
            if (a[i][j] && !visited[i][j])
                rec(i, j);
        }
    }
    cout << res << "\n";
}