[백준 c++] 2632 피자판매

문제

A,B 피자는 각각 다양한 크기의 여러 개의 피자조각으로 나누어져 있다. 고객이 원하는 피자 크기에 맞춰서 줘야하는데 혼합해서 줄수도 있고 한 피자에서 줄 수도 있다. 단, 한 피자에서 2조각 이상을 줄 땐 연속된 조각으로 팔아야한다.
피자가게에서 손님이 원하는 크기의 피자를 판매하는 모든 방법의 가지 수를 계산하는 문제다.

풀이

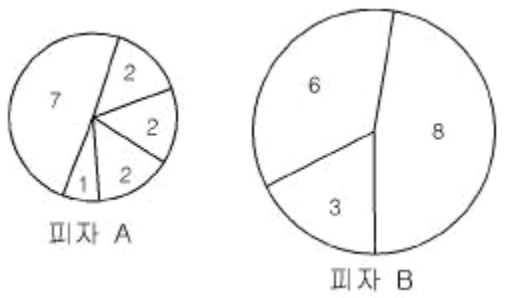
처음에는 각 피자에서 줄 수 있는 조각을 모두 vector에 집어 넣어서 풀었다. 위의 그림에서 피자 B의 벡터에는 {0,3,6,8,9,14,12,24,17}이 들어간다.
이런식으로 A도 구해서 두 벡터값의 합이 k인 경우의 수를 구했는데 시간초과가 났다;;🥲
아마 모든 값을 매번 처음부터 덧셈을 해서 그런 것 같다.

먼저 한 피자에서 몇조각을 가져갈건지에 대한 for문을 이용해서
i = 3이라면 idx 0~3까지 합을 넣고 그 다음부터는 앞의 피자는 빼주고 뒤의 피자를 더해주는 식으로 합을 구했다. 피자는 원형이므로 더해줄 피자 idx는 (제거할 피자idx + 피자 조각 수) % 전체 피자 조각 수 이다.

코드

#include <iostream>
using namespace std;
int k, m, n, res, a[1001], b[1001], Acnt[2000001], Bcnt[2000001];

void go(int p, int arr[], int cnt[])
{
    for (int i = 1; i <= p; i++)
    {
        int sum = 0;
        for (int j = 0; j < i; j++)
            sum += arr[j];
        cnt[sum]++;
        if (sum == k)
            res++;
        if (i == p)
            break;
        for (int j = 1; j < p; j++)
        {
            sum -= arr[j - 1];
            sum += arr[(j + i - 1) % p];
            cnt[sum]++;
            if (sum == k)
                res++;
        }
    }
}

int main()
{
    cin >> k >> m >> n;
    for (int i = 0; i < m; i++)
        cin >> a[i];
    for (int i = 0; i < n; i++)
        cin >> b[i];
    go(m, a, Acnt);
    go(n, b, Bcnt);
    for (int i = 1; i < k; i++)
    {
        int j = k - i;
        res += Acnt[i] * Bcnt[j];
    }
    cout << res << "\n";
}