[백준 c++] 2240 자두나무

문제

https://www.acmicpc.net/problem/2240
인간 자두가 과일 자두를 받아먹으려 한다.

T(1≤T≤1,000)초 동안 자두가 떨어진다.
자두나무는 두 그루다.
인간 자두는 최대 W(1≤W≤30)번 움직일 수 있다.
인간 자두의 초기 위치는 1번 자두나무일 때
인간 자두가 받을 수 있는 자두의 최대 개수를 구하는 문제다.

풀이

단순히 완전탐색으로 풀면 시간초과가 난다.
최대 1000초 동안 1번 나무에 설지 2번 나무에 설지 고르는 경우의 수는 2^1000이기 때문이다.

따라서 DP를 이용해서 풀어야 한다.
dp에 저장할 값으로 3개가 필요하다.
dp[이동횟수][나무번호][현재초]

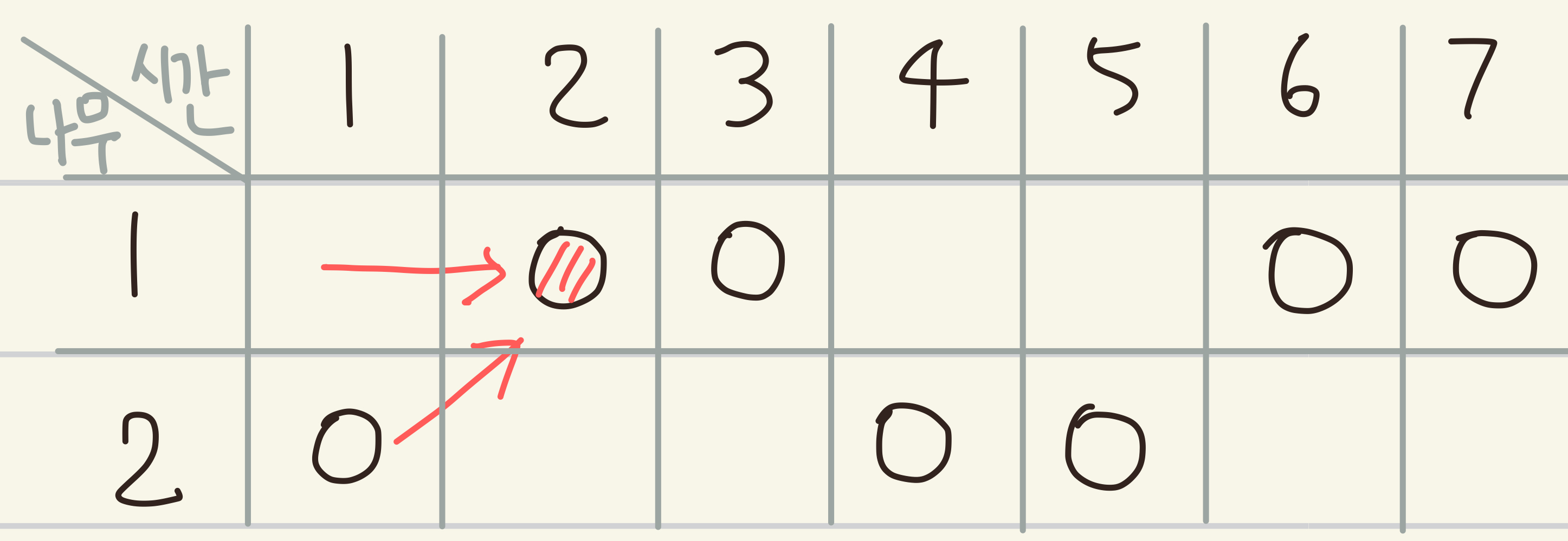
현재 서있는 나무는 이전에는 이전 나무에서 안움직였거나 움직였거나 둘 중 하나다.
그리고 현재 서있는 나무에서 자두가 떨어지면 +1 이다.

이걸로 세운 점화식이다.
(완전탐색이기 때문에 이동횟수(0~W), 시간(1~T)을 이용한 2중 for문을 썼다.)

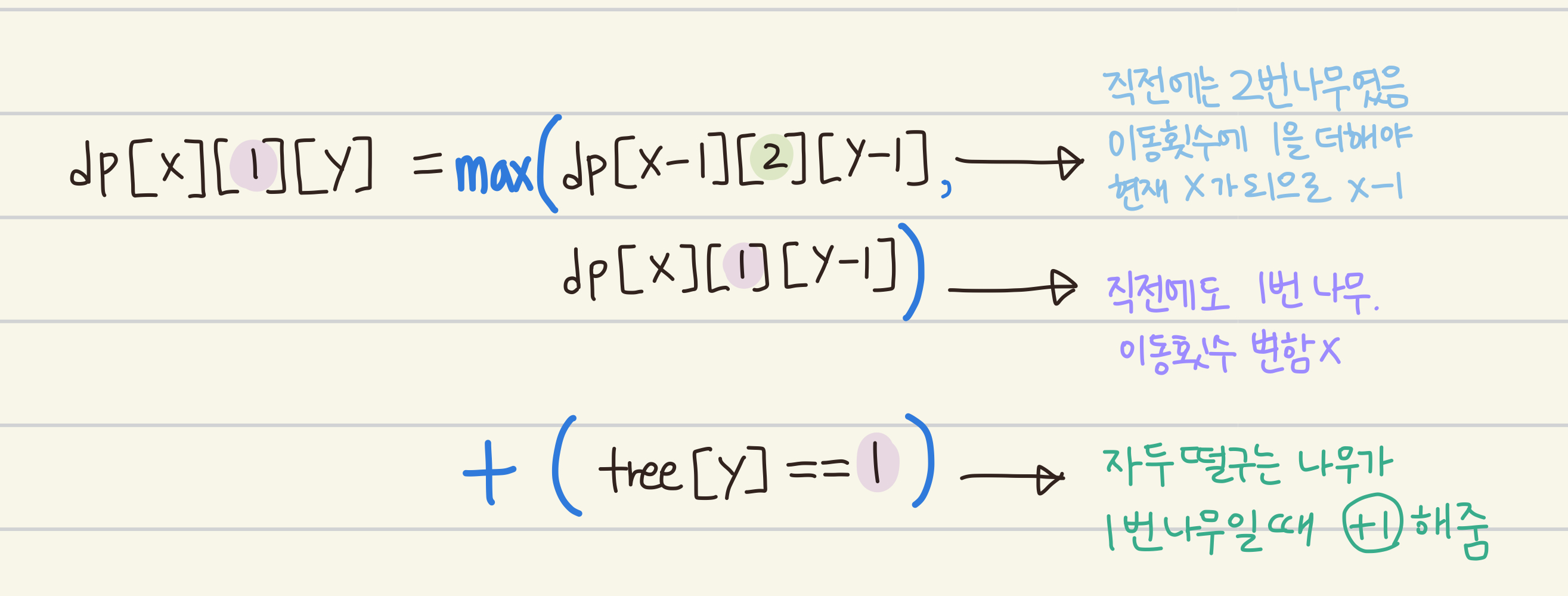
단, 이동 횟수가 0일 때는 움직였을 경우는 고려하지 않는다.

dp[j][0][i] = dp[j][0][i - 1] + (tree[i] == 1); 

계산이 다 끝나면 t초일 때 가장 큰 값을 갖는 dp값을 출력하면 된다.
(t초까지 자두의 최대 개수 구하는게 문제였으니..~🤧)

코드

#include <iostream>
#include <algorithm>
using namespace std;
int t, w, ans;
int tree[1004], dp[31][2][1001];
int main()
{
    cin >> t >> w;
    for (int i = 1; i <= t; i++)
        cin >> tree[i];

    for (int i = 1; i <= t; i++)
    {
        for (int j = 0; j <= w; j++)
        {
            if (j == 0)
            {
                dp[j][0][i] = dp[j][0][i - 1] + (tree[i] == 1);
            }
            else
            {
                dp[j][0][i] = max(dp[j][0][i - 1] + (tree[i] == 1), dp[j - 1][1][i - 1] + (tree[i] == 1));
                dp[j][1][i] = max(dp[j][1][i - 1] + (tree[i] == 2), dp[j - 1][0][i - 1] + (tree[i] == 2));
            }
        }
    }
    for (int i = 0; i < 2; i++)
    {
        for (int j = 0; j <= w; j++)
        {
            ans = max(ans, dp[j][i][t]);
        }
    }
    cout << ans << "\n";
}

DP는 아직 너무 어렵다 ㅜㅁㅜ... 흑흑