[백준 c++] 4811 알약

문제

https://www.acmicpc.net/problem/4811
N개의 알약이 담긴 병에서 매일 알약을 꺼내 먹는다.
근데 하루에 반 알만 먹는다.
그래서 온전한 알약을 꺼냈다면 반 만 먹고 반 알은 다시 병에 집어 넣는다.
한 조각을 꺼낸 날에는 W를, 반 조각을 꺼낸 날에는 H를 기록한다.
총 2N일이 지나면 길이가 2N인 문자열이 만들어지게 된다.
이때, 가능한 서로 다른 문자열의 개수는 총 몇 개일까?

풀이

모든 경우의 수를 살펴봐야 한다.
N = 3일 때 가능한 경우는 아래와 같다.

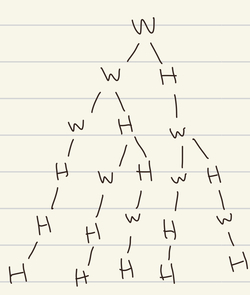
이렇게 그림을 그리고 나니 저번에 풀었던 1103번 게임 문제가 떠올랐다.
거기서도 이렇게 시작점이 정해져 있는 트리 모양이 나왔었고 dp를 이용해서 풀었다.그래서 이 문제도 DP를 이용해서 풀었다.

dp에 어떤 값을 저장해둘까 생각해봤다. 이 문제는 한 알을 꺼냈는지 반 알을 꺼냈는지가 관건이므로 현재까지 꺼낸 각각의 알약 수를 저장하기로 했다.
dp[한 알 꺼낸 횟수(w)][반 알꺼낸 횟수(h)]

1. w와 h가 둘 다 전체 알약 개수와 같아지면 트리의 제일 아래인 리프 노드가 되므로 그 때 return 1을 해준다.

2. dp[w][h] 값이 존재한다면 바로 return

3. dp[w][h] += go(dp[w+1][h])

4. 한 알을 꺼내고 나서야 비로소 반 알이 생기는 거라서
   wtttww처럼 t가 w보다 먼저 더 많이 꺼내지는 것을 불가능하다. 따라서 w > t일 때 dp[w][h] += go(dp[w][h+1])

시행착오
예제는 잘 돌아가는데 자꾸 33%에서 틀렸다고 나왔다. 자잘한게 문젠가 해서 이것저것 수정했는데도 계속 안됐다. 그래서 접근 문제인가? 하고 여러 블로그 풀이를 찾아보는데 나처럼 푸는 사람은 없었고 대부분 go(3,3)에서 시작해서 0으로 가는 식으로 풀었다. 근데 그거나 그거나 똑같은거 아닌가? 하고 내 풀이를 고집해서 풀기로 했다. 그래서 결국 뭐가 문제였냐면 w > t || h > t 인 경우를 고려하지 않아서 문제가 생겼던 것이었다. 알고나니 상쾌했다 🤓

코드

#include <iostream>
#include <algorithm>
using namespace std;
long long t, dp[31][31];
long long go(int w, int h)
{
    if (w == t && h == t)
        return 1;
    if (w > t || h > t)
        return 0;
    if (dp[w][h])
        return dp[w][h];
    if (w > h)
        dp[w][h] += go(w, h + 1);
    dp[w][h] += go(w + 1, h);

    return dp[w][h];
}
int main()
{
    while (1)
    {
        cin >> t;
        if (!t)
            break;
        cout << go(1, 0) << "\n";
        fill(&dp[0][0], &dp[0][0] + 31 * 31, 0);
    }
}