DP를 알아보자

🎯 DP(Dynamic Programming)

필요한 계산 값을 저장해두었다가 재사용하는 알고리즘 설계 기법이다. 동일한 작은 문제들이 반복적으로 계산되는 경우가 생길 수 있다. 그 문제를 매번 다시 계산하지 않고, 값을 저장했다가(메모이제이션) 재사용하는 기법이 바로 DP이다. 메모리 공간을 더 사용하여 시간을 획기적으로 줄일 수 있다.

💡 피보나치 수열

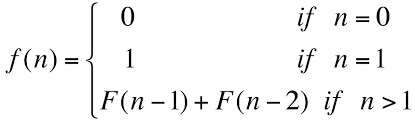
위의 점화식을 python 코드로 나타내면 아래와 같이 나오게 된다.

def fibo(x):
	if x==1 or x==2:
    	return 1
    return fibo(x-1) + fibo(x-2)
    
print(fibo(10))

위의 코드와 같이 실행을 하게 되면 원하는 답이 나오게 되어있다. 아무리 큰수라도 위의 코드에 적용시켜도 잘 나온다. 하지만!!! 우리가 원하는 것은 효율적인 코드이다. 아무리 큰 수를 넣어서 오래 기다리는 시간과 불렀던 것을 다시 불러오는 비효율적인 코드는 피해야 한다.

💡 Topdown

👉 Memoization
메모이제이션은 컴퓨터 프로그램을 실행할 때 이전에 값을 메모리에 저장해서 매번 다시 계산하지 않도록 하여 전체적인 실행속도를 빠르게 하는 기술이다. DP의 핵심이다. 위의 피보나치 코드를 Topdown방식으로 작성해보겠다.

memo = [0, 1]
def fibo(n):
    if n >= 2 and len(memo) <= n:
        memo.append(fibo(n-1) + fibo(n-2))
    return memo[n]

실행해서 print()해보면 알겠지만 리스트에 저장을 해두고 나중에 다시 꺼내 쓰는 방법을 사용하여 구현되어 있다.

💡 Bottomup

👉 Tabulation
하위 문제부터 천천히 해결하면서 더 큰 문제를 해결하는 기법을 말한다. Tabulation이라고 부르는 이유는 작은 문제부터 큰 문제까지 하나하나 테이블을 채워간다는 의미때문이다. DP의 전형적인 형태는 바로 이 bottomup방식이다.

memo = [0,1,1] + [0]*(n-3)
n = 99
for i in range(3, n+1):
	memo[i] = memo[i-1] + memo[i-2]

🎯 백준 문제

https://www.acmicpc.net/problemset?sort=ac_desc&algo=25

1003 피보나치 함수

import sys
input = sys.stdin.readline

largest = max(nums := [int(input()) for i in range(int(input()))])
memo = [[1,0], [0,1], [1,1]] + [[0,0]]*(largest-2)

for i in range(3, largest+1):
    memo[i] = [memo[i-1][0]+memo[i-2][0], memo[i-1][1]+memo[i-2][1]]
    
for i in nums:
    print(*memo[i])

가장 큰 수(largest)를 찾아서 largest만큼만 돌리고 입력받은 인덱스를 찾아서 출력하는 방식이다.

2579 계단 오르기

import sys
input = sys.stdin.readline

n = int(input())
m = [int(input()) for _ in range(n)] + [0] * (301-n)

dp = [0] * 301 # 계단
dp[0] = m[0] # 첫 번째 계단
dp[1] = m[0] + m[1] # 두 번째 계단
dp[2] = max(m[1] + m[2], m[0] + m[2]) # 연속으로 세 개의 계단을 밟는 경우와 두 계단을 한번에 오르는 경우를 비교

# 반복문을 통해 계단을 오른다.
for i in range(3, n + 1):
    dp[i] = max(dp[i - 3] + m[i - 1] + m[i], dp[i - 2] + m[i]) # 연속으로 세 개의 계단을 밟는 경우와 두 계단을 한번에 오르는 경우를 비교

print(dp[n - 1])

1. 첫 번째 계단
   DP[0] = stair[0]

2. 두 번째 계단
   DP[1] = stair[0] + stair[1]

3. 세 번째 계단
   DP[2] = stair[1] + stair[2] 혹은 stair[0] + stair[2] 둘 중 큰 값을 고른다.

4. 네 번째 계단
   DP[3] = stair[0] + stair[1] + stair[3] + stair[4] 혹은 stair[0] + stair[2] + stair[4]

네 번째 계단을 보면, 겹치는 값들이 보입니다. 해당 값을 DP를 활용해서 변경하면
DP[1]+stair[3]+stair[4] 혹은 DP[2]+stair[4] 이렇게 나온다.
위에 두 개의 식 중에 더 큰 값을 DP에 저장하게 됩니다. 이를 점화식으로 나타내면 다음과 같다.

DP[i] = max(DP[i-3] + stair[i-1] + stair[i], DP[i-2]+stair[i])

1912 연속합

import sys
input = sys.stdin.readline

n = int(input())
m = list( map(int, input().split()))

for i in range(1, n):
    m[i] = max(m[i], m[i] + m[i-1])

print(max(m))

정리

DP는 걀괏값을 얻기 위한 과정을 쌓아가는 것입니다. 이전 결과 값을 활용해 N번째에서 최선의 값을 얻을 수 있습니다.