[혼공머신] 2주차-회귀

ℹ️ <혼자 공부하는 머신러닝+딥러닝> 책을 읽고 정리한 내용입니다.

2주차에는 chapter3: 회귀 알고리즘과 모델 규제를 읽었다.

이번 주 분량을 보며 가장 좋았던 점은, 그동안 어렴풋이 들어봤던 회귀, 모델, 피쳐, 훈련, 오버피팅 같은 개념들을 처음부터 차근히 정리할 수 있었다는 데 있다. 무엇보다 왜 피쳐가 중요한지, 그리고 그 피쳐로 어떻게 모델을 훈련하고, 오버피팅을 방지하는지 전체적인 흐름을 이해할 수 있었다.

특히 피쳐 사이의 조합을 통해 새로운 피쳐를 만들 수도 있기 때문에, 최초의 피쳐 자체가 매우 중요하다는 사실도 인상 깊었다.

분류 vs 회귀

지도 학습은 크게 두 가지로 나뉜다.

• 분류(classification): 샘플을 몇 개의 클래스 중 하나로 분류
  - 예시: 이 물고기의 크기와 무게를 봤을 때, 도미일까 빙어일까?
• 회귀(regression): 임의의 숫자를 예측
  - 예시: 이 물고기의 길이·높이·두께를 봤을 때, 무게가 얼마나 될까?

참고로 처음엔 '회귀'라는 용어가 조금 낯설었는데, 평균으로 회귀한다라는 문장을 보고 어떤 맥락에서 사용되는지 감을 잡았다.

결정계수(R²)

회귀 모델은 정답이 하나의 숫자이기 때문에, 분류 모델처럼 "맞았다/틀렸다"로 평가할 수 없다. 대신 결정 계수 R²로 성능을 평가한다.

R² = 1 - {(타깃-예측)²의 합} / {(타깃-평균)²의 합} = (예측 오차) / (기본 오차)

분자를 '예측한 것의 오차값'으로, 분모를 '평균을 활용하는 기본적인 오차값'으로 이해해볼 수 있다.

최종적인 (예측 오차) / (기본 오차)는 아래 중 하나이다. 각각의 의미를 함께 생각해보자.

• 0: 예측을 아주 잘한 경우 예측 오차는 0에 수렴한다. 그러면 이 분수도 0이 된다.
• 1: 예측 오차값이 평균으로 예측한 것과 다를 바 없는 경우 분수가 1이 된다.
• 1보다 크다: 이건 완전 예측이 빗나간 경우.

이제 1에서 뺀 결과를 살펴보면,

• 예측이 완벽: 1 - 0 = 1 (최고!)
• 예측이 평균 수준: 1 - 1 = 0 (그냥 평균만 예측하는 수준)
• 예측이 평균보다 못함: 1 - 1.5 = -0.5 (평균보다 못함)

즉, R² 값이 1에 가까울수록 좋은 모델이다.

과대적합 vs 과소적합

훈련 데이터의 R²과 테스트용 데이터의 R²를 비교하여 모델 훈련이 얼마나 잘 되었는지를 판단할 수 있다. 보통은 훈련 데이터의 R²값이 테스트용 R²보다 높게 나온다.

훈련이 잘 안 된 경우를 두 가지로 분류해볼 수 있는데, '과대적합'과 '과소적합'이 그것이다.

과대적합(overfitting)

• 훈련용 R²이 테스트용 R²보다 지나치게 높은 경우를 '과대적합(overfitting)'이라고 한다.
• 다시말해, 훈련 데이터에 과하게 fitting되어 있다는 의미이다. 훈련 데이터만 잘 맞추고, 테스트 데이터는 거의 잘 못 맞추기 때문이다.
• 이를 해결하기 위해 '규제'를 하는데, 이에 대해서는 아래에서 더 자세히 설명하도록 하겠다.

과소적합(underfitting)

• 훈련용 R²보다 테스트용 R²이 높은 상황이다.
• 즉, 훈련이 잘 안 되었다고 볼 수 있다.
• 보통 훈련 데이터가 적은 경우 발생하는 문제이다.

만약 K-NN 알고리즘에서 과소적합 문제가 발생한다면, K값을 줄여볼 수 있다. 그렇게 하면 '전반적인' 데이터로부터 받는 영향이 줄어들고 '주변' 데이터로부터 받는 영향이 커지기 때문이다.

n_neighbors 값에 따른 모델 변화

확인문제 2번을 통해 n_neighbors 값에 따른 모델 변화를 살펴보자.

K-NN 알고리즘에서 n_neighbors 값을 변화시키면 모델의 복잡도가 달라진다.
아래 그림처럼 n=1일 땐 훈련 데이터에 매우 민감하게 반응하고, n=10일 땐 훨씬 더 단순한 형태가 된다.

n=1	n=5	n=10

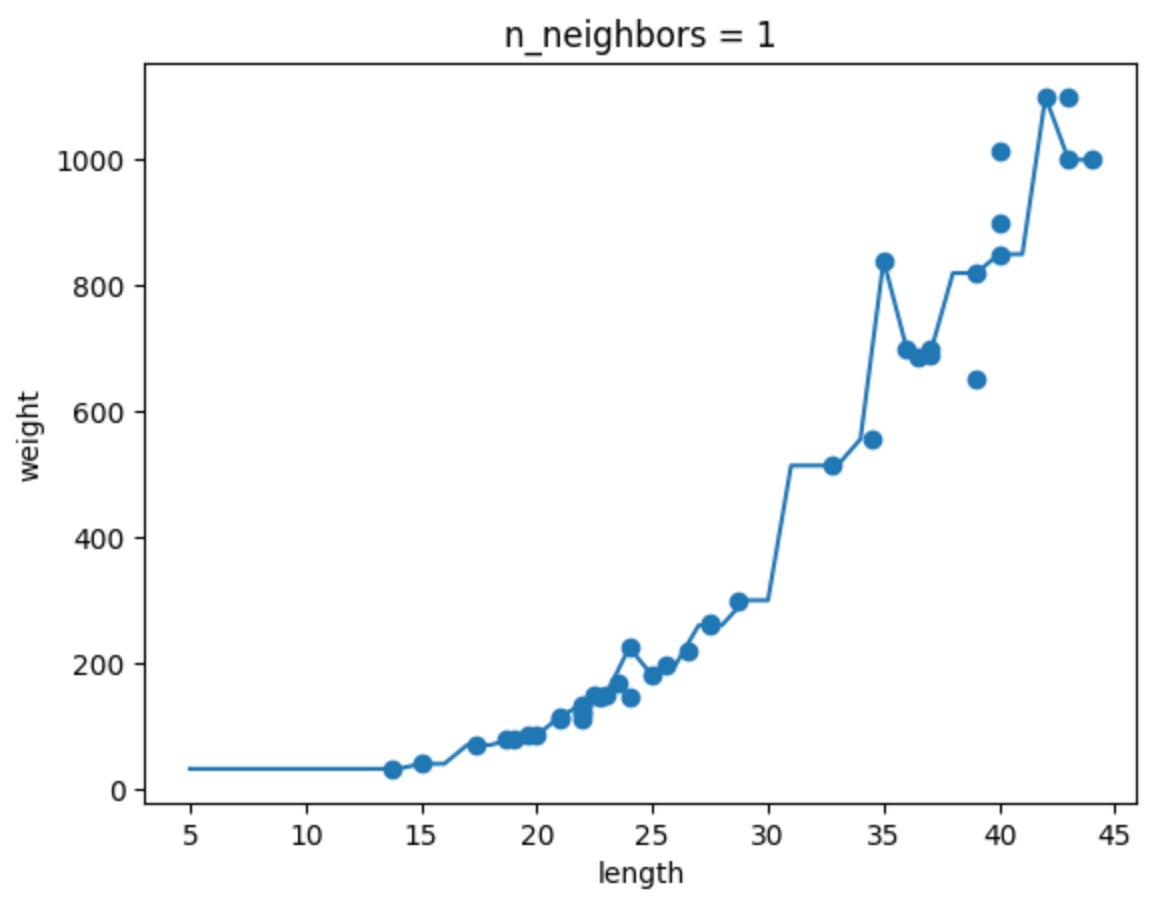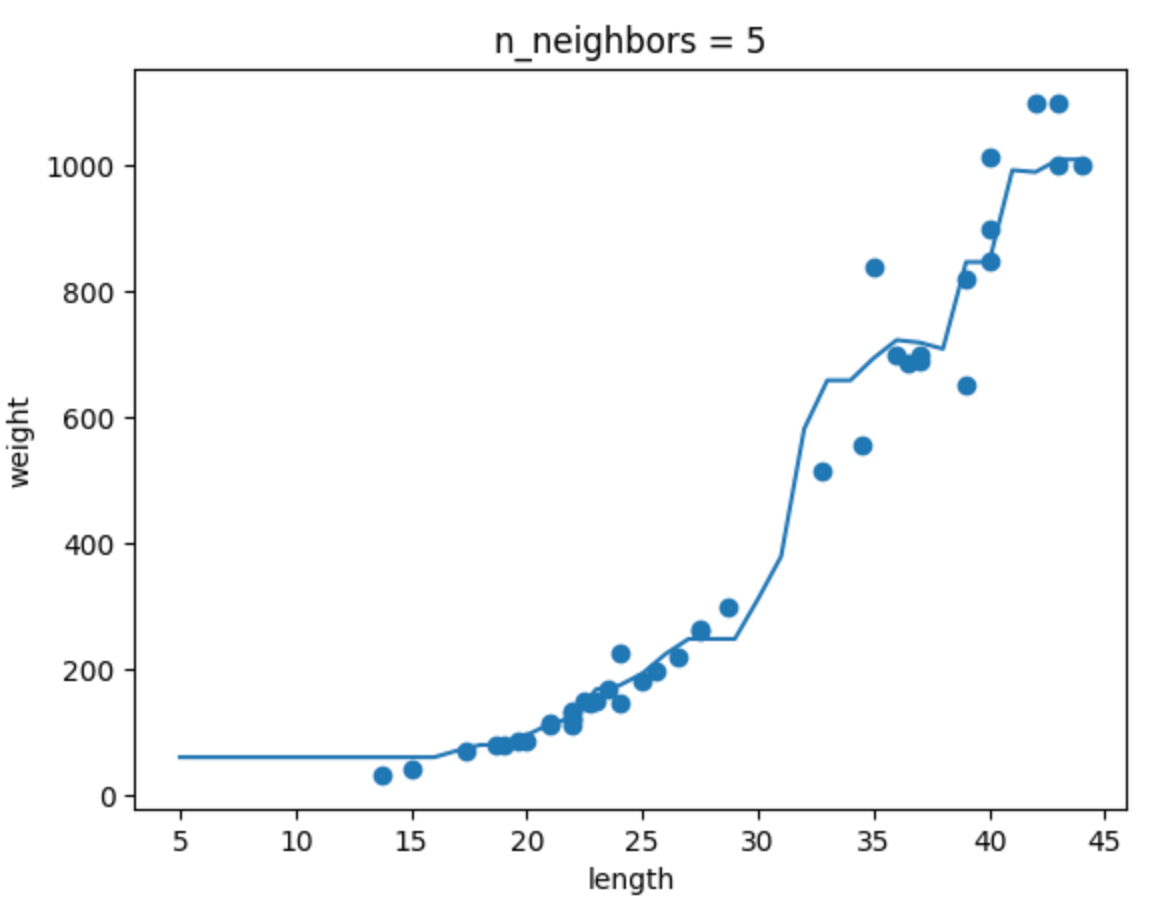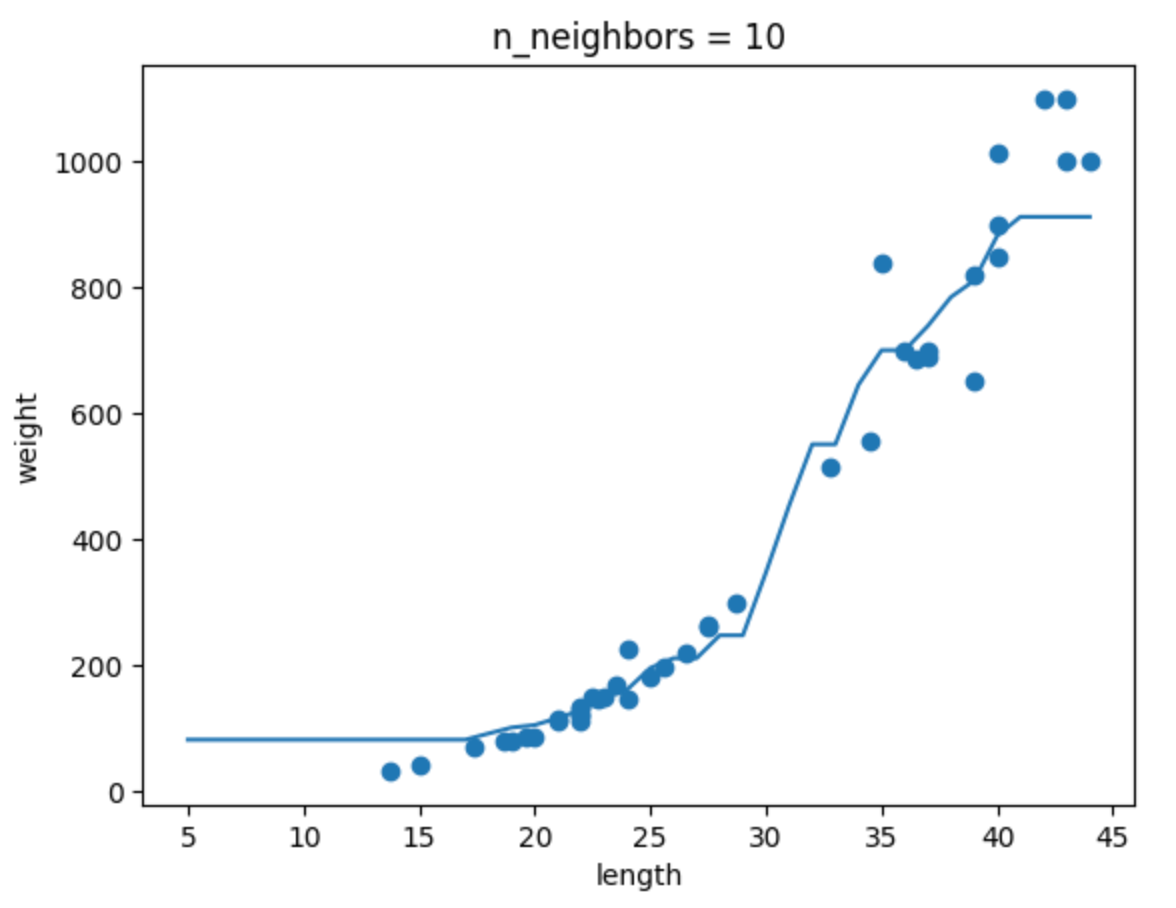선형회귀와 다항회귀

KNN의 한계를 극복하려면?

KNN은 훈련 범위를 벗어난 값을 예측하지 못한다. 예를 들어 훈련 데이터가 0~45cm 범위의 물고기 길이였다면, 50cm 물고기는 예측이 어렵다.

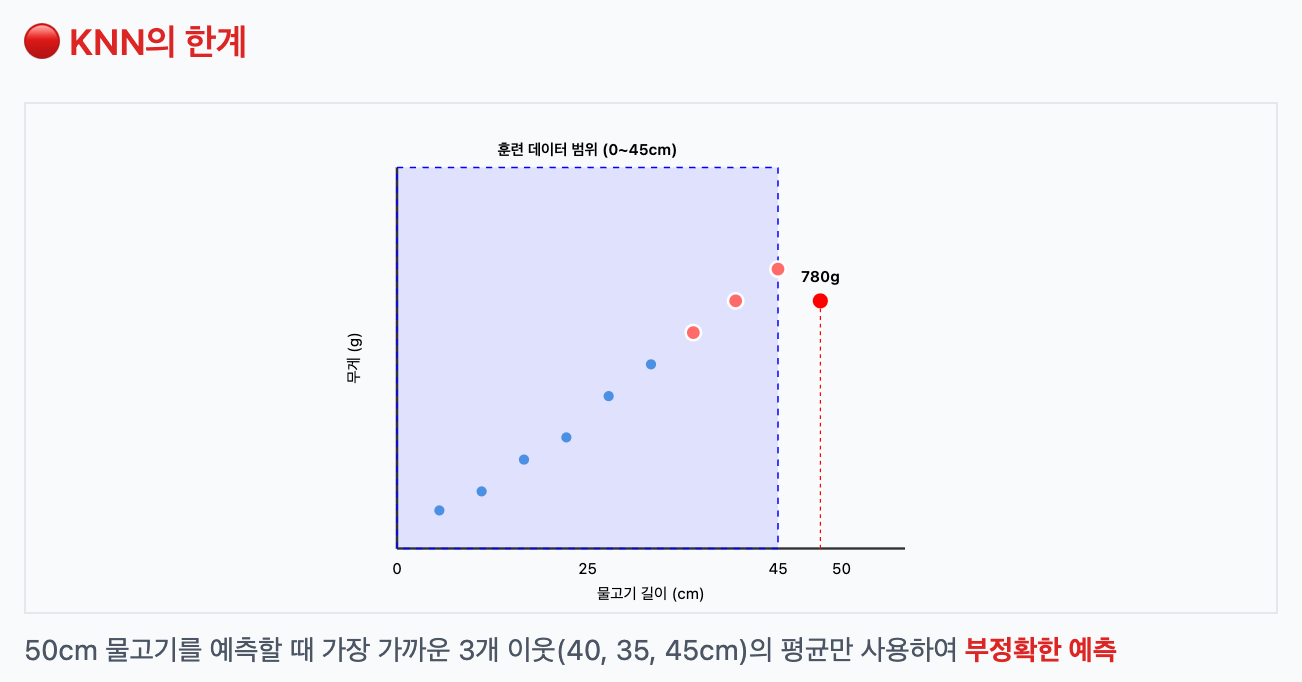
이럴 때 사용하는 것이 바로 선형회귀(linear regression). 선형회귀는 1차 함수 형태로 데이터를 모델링하기 때문에, 범위를 벗어난 값도 예측할 수 있다.

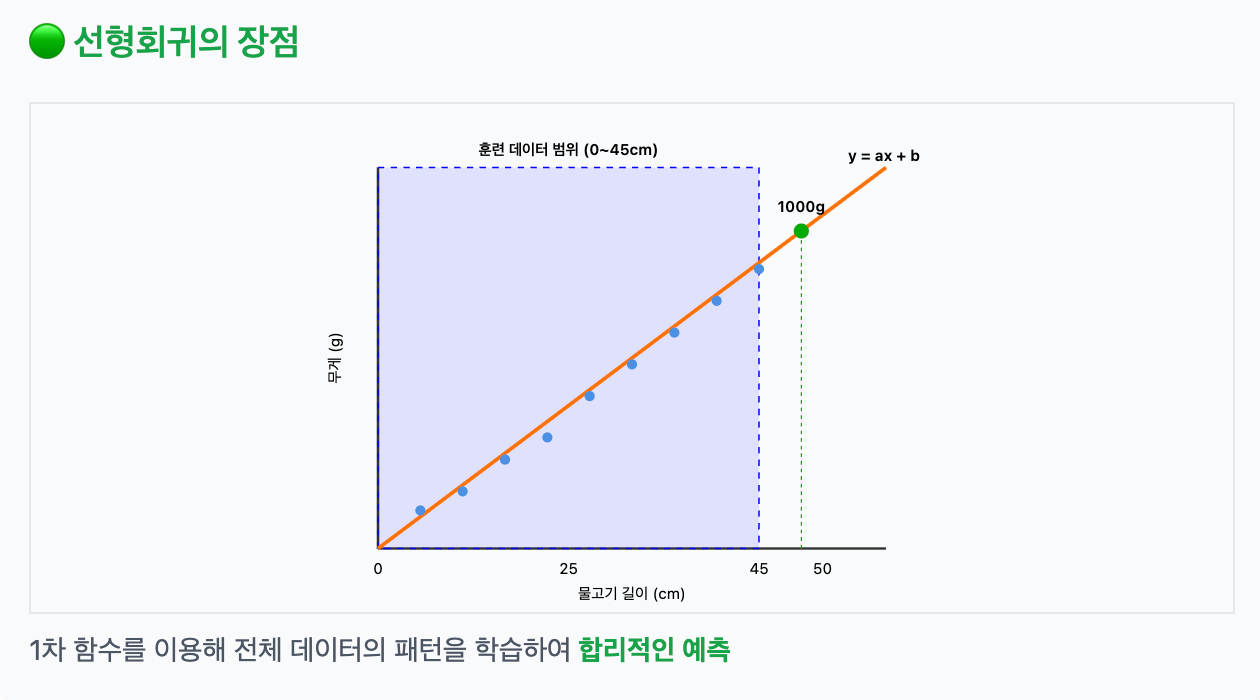
하지만 데이터가 꼭 직선으로 증가할까?

항상 데이터가 선형적으로 올라간다는 보장은 없다. 경우에 따라 데이터가 곡선 형태일 수도 있다.

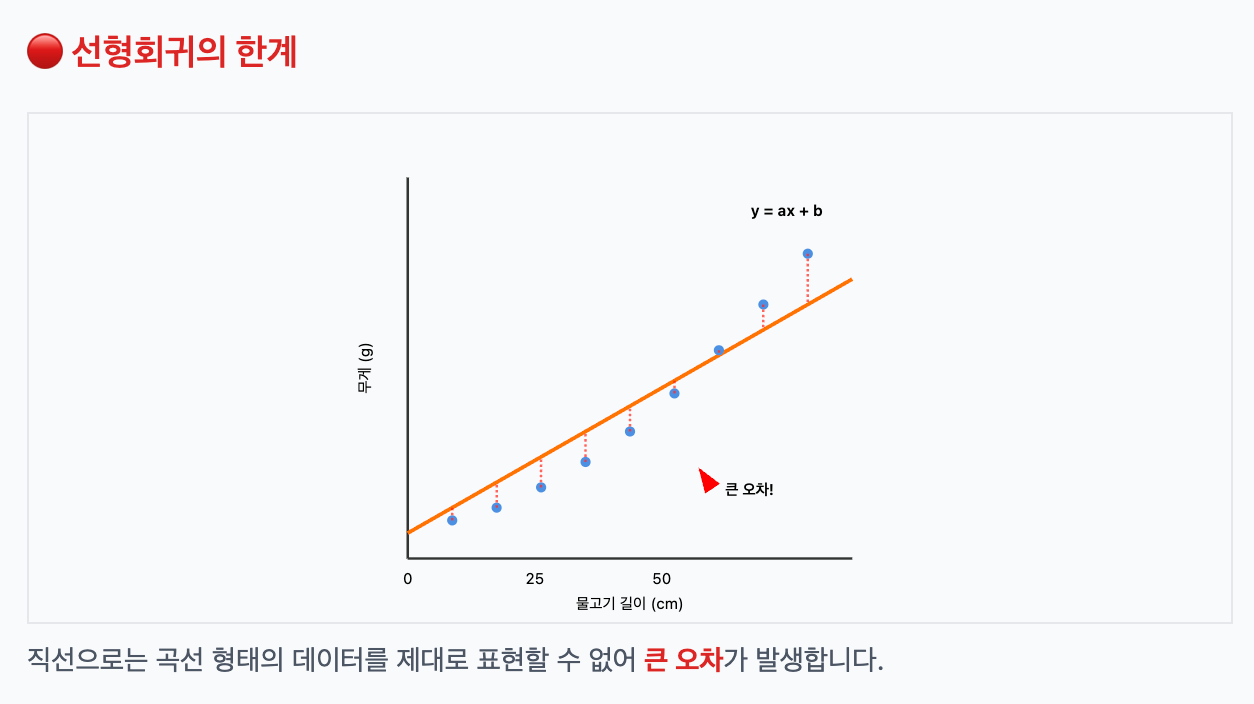
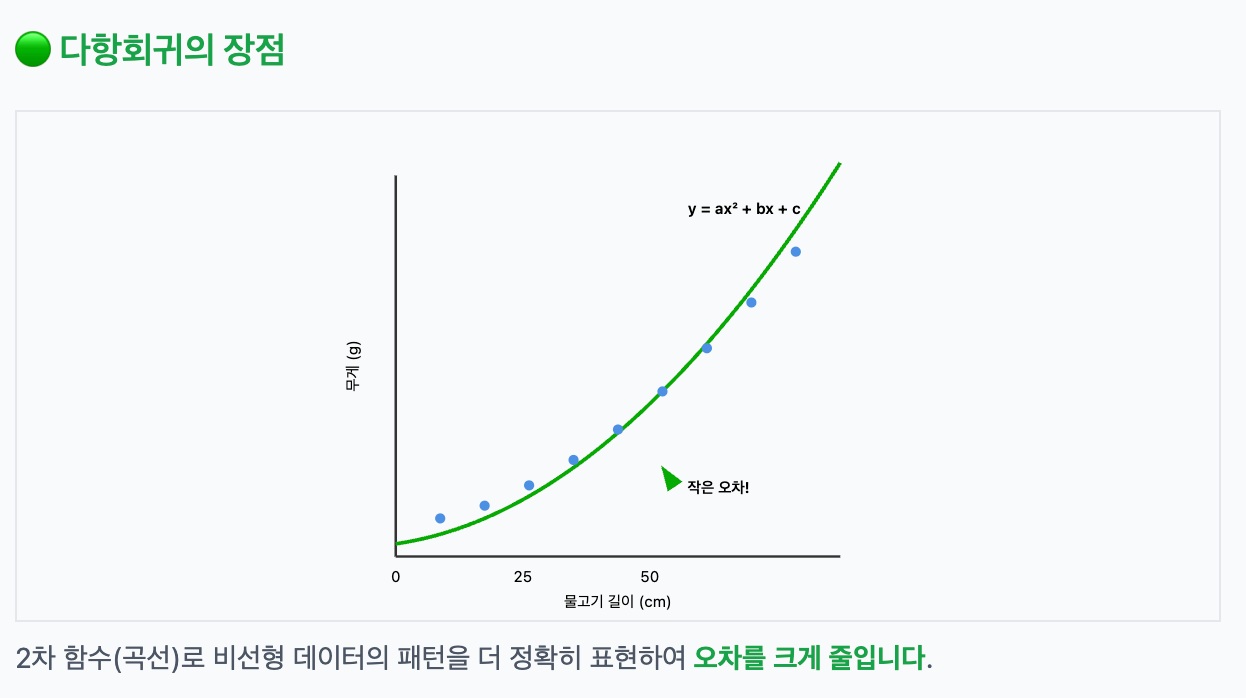
이럴 땐 다항회귀(polynomial regression)를 사용하면 더 나은 예측이 가능하다.

모델 파라미터

모델 파라미터는 linear에서의 y=ax+b의 a와 b, polynomial에서의 y=ax^2+bx+c에서의 a,b,c를 의미한다. 즉 방정식의 계수들을 '모델 파라미터'라고 부른다.

다중 회귀

앞선 선형회귀를 다시 떠올려보자. y=ax+b 공식을 곱씹어보면, x라는 피쳐 하나로 y를 예측하고 있다. 피쳐를 두 개 이상 사용해볼 수는 없을까?

단일 피쳐가 아닌, 여러 피쳐를 활용할 수 있는 회귀 방법이 있다. 이를 다중 회귀(multiple regression)라고 한다.

예를 들어 길이, 높이, 두께라는 피쳐가 있다면 아래처럼 식이 나올 수 있을 것이다.

y = a₁*길이 + a₂*높이 + a₃*두께 + b

특성 공학 (Feature Engineering)

특성 공학이란 피쳐끼리 곱하거나 제곱하여 새로운 특성을 만드는 기법이다.

농어의 길이, 높이, 두께 세 가지 정보를 알고 있는 상태에서 농어의 무게를 예측하는 상황을 생각해보자. 이 때에는 농어의 길이와 높이 각각보다도, 둘을 곱한 농어 길이 * 농어 높이를 새로운 피쳐로 볼 수도 있는 거다. 이런 방식으로 특성과 특성을 조합하여 새로운 특성을 뽑아내는 것을 특성 공학(feature engineering)이라고 부른다.

특성을 추가하여 모델을 훈련하고 평가하는 전체 흐름

특성 공학이 모델 훈련에 어떻게 사용되는지 알아보자.

1. 피쳐 준비 (원본)
   원본_피쳐 = [길이, 높이, 너비]

2. 피쳐 가공
   poly.fit(원본_피쳐) # "2차 항들도 만들어야겠다"
가공된_피쳐 = poly.transform(원본_피쳐) # [길이, 높이, 너비, 길이², ...]

3. 모델 훈련 (진짜 훈련!)
   model.fit(가공된_피쳐, 타겟) # w₁, w₂, w₃, w₄... 계수들 찾기

구체적인 코드는 아래와 같다.

피쳐 전처리 프로세스를 다음과 같이 진행한다. train_input(훈련용)과 test_input(평가용) 데이터 모두 피쳐 늘리기를 진행해준다.

# 피쳐 전처리 프로세스임. fit() -> transform()
# train_input, test_input 모두 피쳐 늘리기를 동일하게 해주어야함.
from sklearn.preprocessing import PolynomialFeatures
poly = PolynomialFeatures(include_bias=False)
poly.fit(train_input)

train_poly = poly.transform(train_input)
test_poly = poly.transform(test_input)

print(train_input.shape, test_input.shape) # (42, 3) (14, 3)
print(train_poly.shape, test_poly.shape) # (42, 9) (14, 9)

shape을 찍어보면, 피쳐가 3개에서 9개로 늘어난 것을 확인할 수 있다.

그리고 이제 모델을 훈련시킨 뒤 평가를 진행해보자.

# 다중 회귀 모델 훈련 프로세스임.
from sklearn.linear_model import LinearRegression
lr = LinearRegression()
# 훈련
lr.fit(train_poly, train_target)
# 평가
print(lr.score(train_poly, train_target)) # 0.9903183436982125
print(lr.score(test_poly, test_target)) # 0.9714559911594111

과적합과 규제

과적합 사례

위 코드에서 한 줄만 이렇게 바꾸어 보았다.

degree=5로 다항 회귀를 구성하자 피쳐 수가 55개로 늘어났다.

poly = PolynomialFeatures(degree=5, include_bias=False)

print(train_input.shape, test_input.shape) # (42, 3) (14, 3)
print(train_poly.shape, test_poly.shape) # (42, 55) (14, 55)

훈련 결과는 처참했다..! 훈련용 데이터는 높은 확률로 다 맞추었지만, 테스트 결과는 아주 큰 음수가 나와버린 것이다.

print(lr.score(train_poly, train_target)) # 0.9999999999996433
print(lr.score(test_poly, test_target)) # -144.40579436844948

이러한 상황을 '과적합(overfitting)' 문제라고 한다.

이를 보완하기 위해서 '규제'라는 기법을 사용할 수 있다.

규제(Regularization)

머신러닝 모델이 훈련 세트를 너무 과도하게 학습하지 못하도록 훼방하는 것을 '규제'라고 한다.

선형회귀 모델에 규제를 추가한 모델을 활용할 수 있다. 특히 릿지(ridge)와 라쏘(lasso)가 있다.

이 때 모델에 alpha 값을 넣어서 규제의 양을 임의로 조정할 수 있다. alpha 값이 작을수록 제어를 덜 한다고 보면 된다. 즉, 과대적합이 나타날 확률이 높아지는 것이다.

이 alpha값은 모델이 따로 계산을 통해 도출하는 것이 아니라 사람이 직접 넣어주는데, 이처럼 사람이 지정하는 값을 '하이퍼파라미터'라고 부른다.