
ℹ️ <혼자 공부하는 머신러닝+딥러닝> 책을 읽고 정리한 내용입니다.
로지스틱 회귀
- 상황: 럭키백에서 7종의 물고기 중 각 물고기가 나올 확률을 예측하는 상황
- KNN의 한계: 이웃한 샘플 클래스의 비율로만 확률을 계산하면 제한적인 확률값만 나옴
- K=3일 때 A 물고기일 확률은 0/3, 1/3, 2/3, 3/3 중 하나만 가능
- 0/3 (0%): 이웃 3개 중 아무도 A물고기가 아닌 경우
- 1/3 (33.3%): 이웃 3개 중 A물고기가 1개인 경우
- 2/3 (66.7%): 이웃 3개 중 A물고기가 2개인 경우
- 3/3 (100%): 이웃 3개 중 모두 A물고기인 경우 - 로지스틱 회귀는 이름은 '회귀'지만 실제로는 분류 모델
- 선형 회귀처럼 선형 방정식을 활용:
z = a × feature1 + b × feature2 + c × feature3 + d × feature4 + e × feature5
이진 분류와 시그모이드 함수
- z값은 어떤 값이든 가질 수 있지만, 확률은 0과 1 사이여야 함
- 시그모이드 함수로 z값을 0~1 사이로 압축:
확률 = 1 / (1 + e^(-z)) - 이진 분류에서는 z값 하나만 계산하면 됨
- 한 클래스 확률을 구하면, 다른 클래스 확률은 자동으로1 - 확률
다중 분류와 소프트맥스 함수
- 소프트맥스 함수는 여러 개의 z값을 모두 0~1 사이로 압축하면서 전체 합이 1이 되도록 만듦
- 다중 분류에서는 각 클래스마다 별도의 z값 필요:
- 7종 물고기 → 7개의 z값 (z1, z2, ..., z7)
- 한 클래스의 확률을 알아도 나머지 클래스들의 확률을 자동으로 알 수 없기 때문z1 = a1×길이 + b1×무게 + c1×대각선길이 + ... (도미용) z2 = a2×길이 + b2×무게 + c2×대각선길이 + ... (빙어용) z3 = a3×길이 + b3×무게 + c3×대각선길이 + ... (농어용) ... z7 = a7×길이 + b7×무게 + c7×대각선길이 + ... (7번째 물고기용) - 이진 분류와 달리 다중 분류는 각 클래스에 대해 독립적인 선형 방정식이 필요
확인문제(4-1)
이제 위에서 정리한 내용에 대한 확인문제 해설을 해본다.
Q. 로지스틱 회귀가 이진 분류에서 확률을 출력하기 위해 사용하는 함수는 무엇인가요?
→ 답은 당연히 시그모이드 함수!
시그모이드 함수에 대해서는 위의 내용을 참고하시라.
확률적 경사 하강법
- 경사 하강법: 훈련 세트에서 하나의 샘플씩만 사용해 가중치를 업데이트하는 방법
- '확률적': 샘플을 꺼낼 때 랜덤으로 꺼낸다
- 가중치: 여기서 가중치란, 피쳐에 곱해지는 상수임 (위에 로지스틱 공식에서 언급한 a, b, c등)
- 과정은 대략 이런 느낌
1. 현재 가중치로 예측 → 손실 계산- "가중치를 조금 늘리면 손실이 줄어들까? 늘어날까?" → 경사 계산
- 손실이 줄어드는 방향으로 가중치 조정
- 이 과정 반복
- 에포크(Epoch): 확률적 경사 하강법에서 전체 샘플을 모두 사용하는 한 번의 반복을 의미함
- 랜덤으로 샘플을 뽑아 사용하기 때문에 매 에포크마다 최종 가중치가 달라질 수 있음- 가장 최적을 찾기 위해 수십에서 수백 번의 에포크를 반복한다
손실 함수
- 목표: '모델이 얼마나 틀렸는지'를 숫자로 측정하는 것
- 손실 함수를 통해 나온 손실들은 미분 가능하도록 연속적이어야 한다
- 연속적인 손실 분포를 만드는 데에 로지스틱 손실 함수를 생각해볼 수 있다. (위의 물고기 분류 내용에 따르면, 기존의 KNN은 4가지 숫자가 반복되던 것과 달리 로지스틱은 다양한 숫자가 나오기 때문)
로지스틱 손실 함수
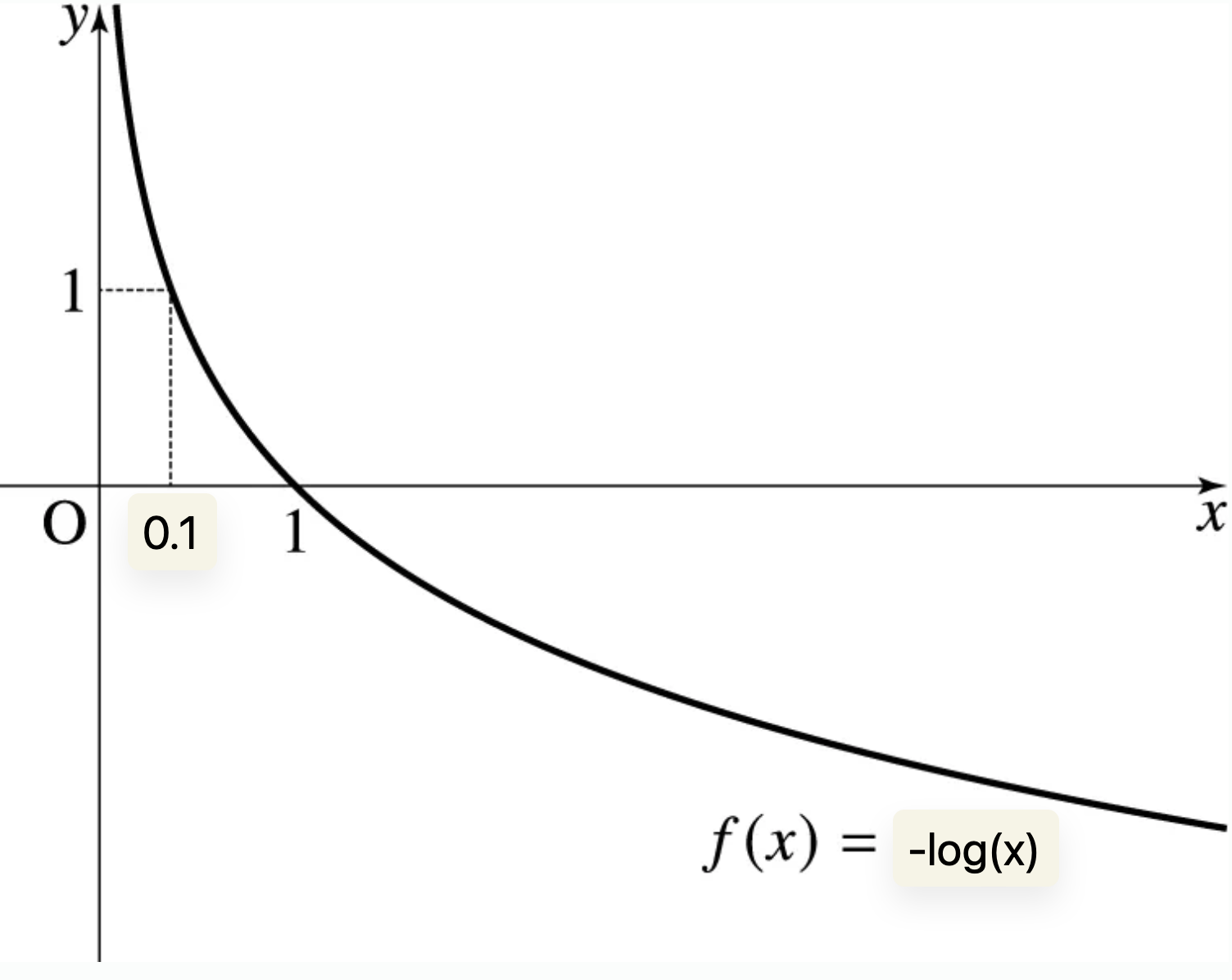
- 예측 확률이 1에 가까울수록 손실은 적고, 0에 가까울수록 손실은 크다
- 이를 보다 명료하게 표현할 방법으로
-log(예측확률)이 있음 -log(x)함수는 예측을 못했을수록(0에 가까울수록) 큰 손실임을 나타낼 수도 있어 굿
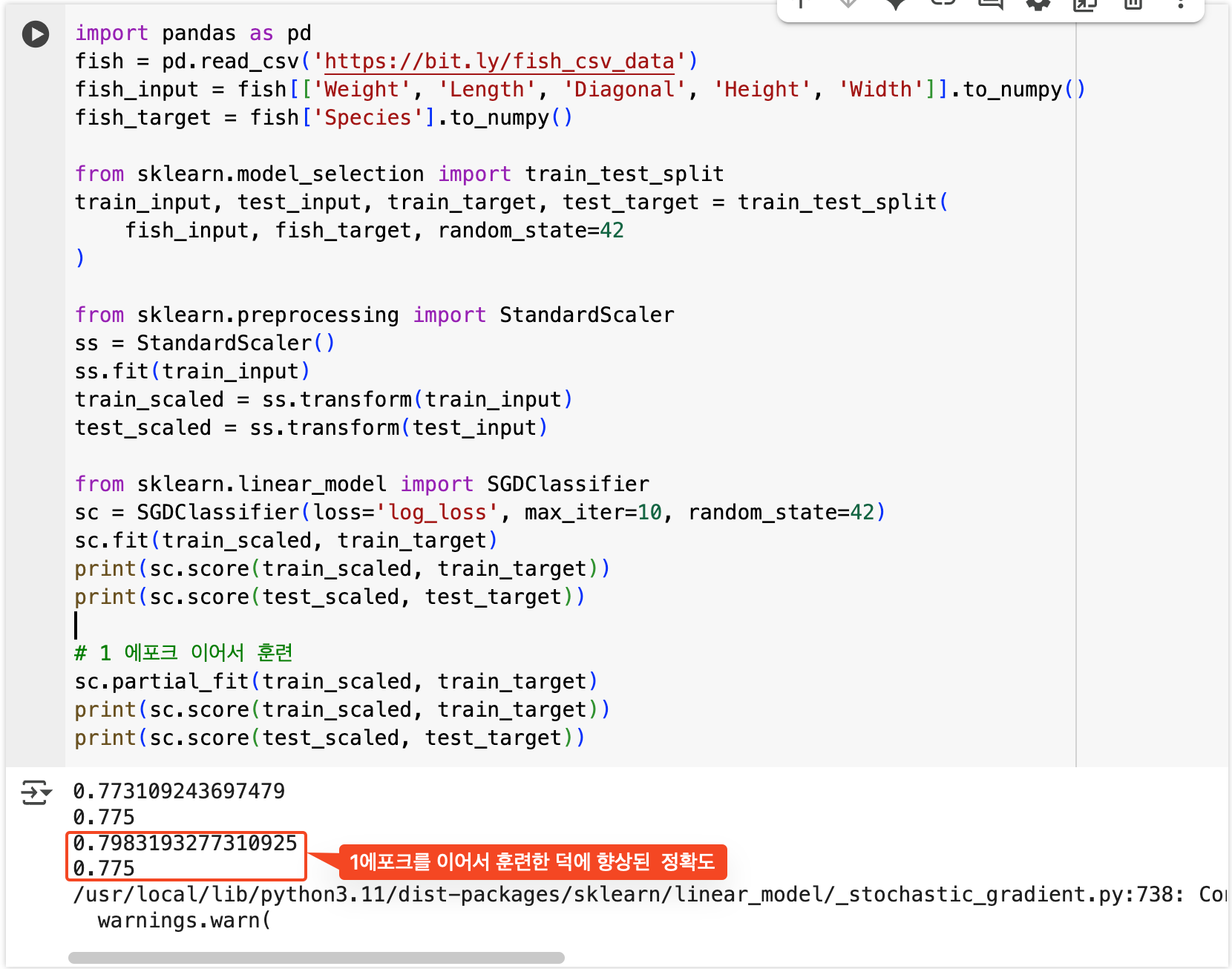
실제로 SGDClassifier로 구현해보기
에포크 횟수에 따른 과대/과소 적합
- 과소 적합: 에포크 횟수가 적으면 훈련이 덜 되어 발생
- 과대 적합: 에포크 횟수가 많으면 훈련이 너무 잘 돼 발생
- 조기 종료: 과대 적합이 시작되기 전에 훈련을 멈추기
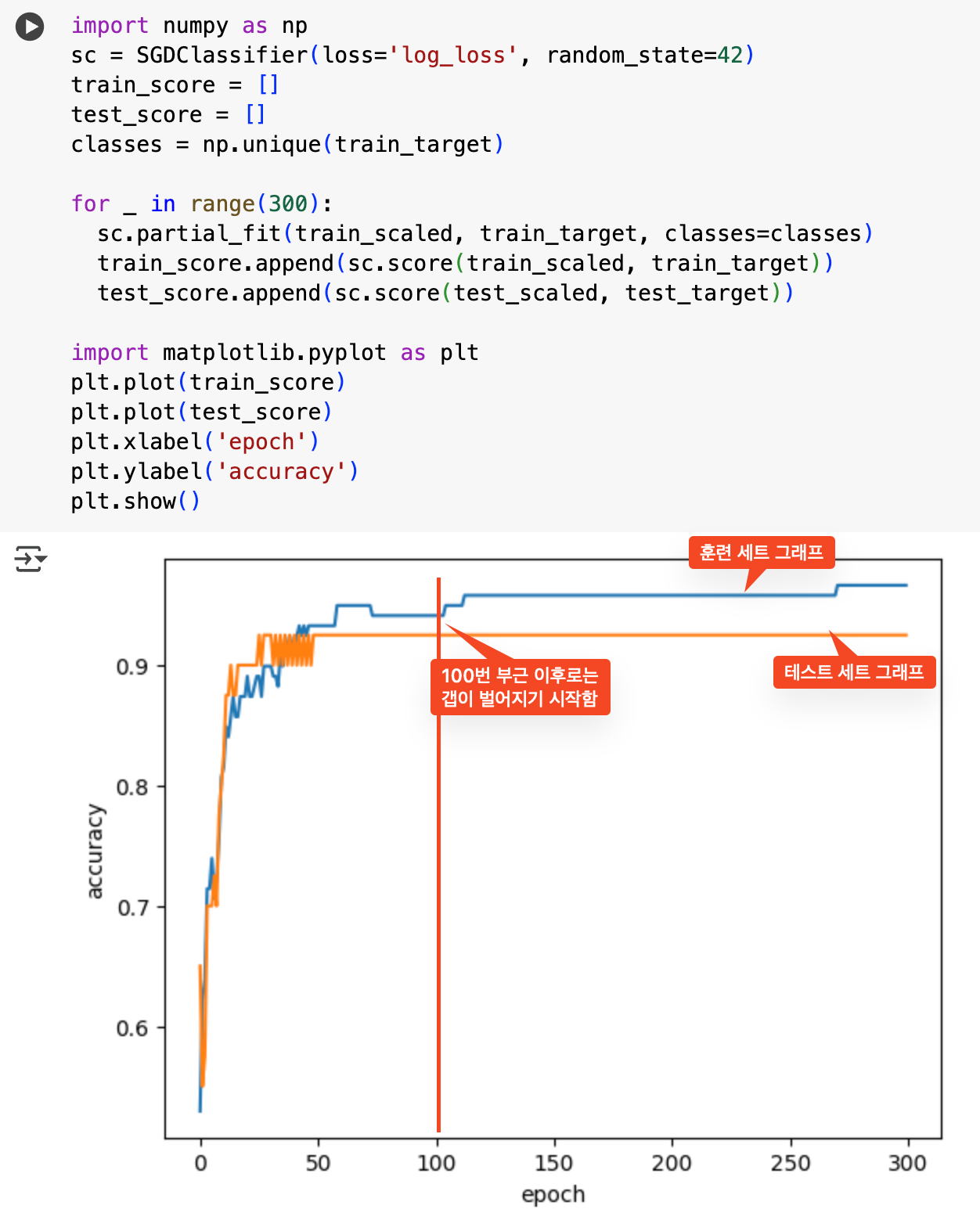
위의 그래프를 봤을 때, 100에서 조기종료 해주면 나이스
