📌 객체 탐지 모델을 공부하다 논문에 Smooth L1 Loss가 자주 나와서 정리해보려 합니다. 하는 김에 L1 loss와 L2 loss도 같이 정리해보겠습니다.
🔶 L1 Loss (Mean Absolute Error) & L2 Loss (Mean Square Error)
L1 Loss
이 손실 함수는 예측값과 실제값 간의 절대적 차이를 계산합니다.
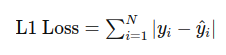
L1 Loss는 각 샘플의 예측값과 실제값 간의 절대적인 차이를 계산합니다. 이 차이는 예측이 실제값보다 클 때는 양수, 작을 때는 음수입니다. 모델의 예측이 실제값과 얼마나 가까운지를 평가하는 데 유용하며, 특히 데이터에 이상치가 포함된 경우에 효과적입니다.
L2 Loss
이 손실 함수는 예측값과 실제값 간의 제곱 오차를 계산합니다.
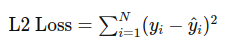
L2 Loss는 예측값과 실제값 간의 차이를 제곱하여 계산합니다. 이 제곱 연산은 오차가 클수록 손실 값이 더 크게 증가하도록 만듭니다.
👉 L1 Loss와 L2 Loss의 장단점을 알아봅시다.
L1
L1 Loss는 이상치에 덜 민감하여, 데이터에 극단적인 값이 포함된 경우에도 안정적인 학습을 할 수 있습니다. 절대 오차를 직접 측정하기 때문에 결과의 해석이 비교적 간단합니다.
하지만 절댓값 함수의 경우 V자 모양을 그리며 미분이 불가능한 지점이 있습니다. 미분을 통해 역전파를 수행하는 딥러닝 모델에 있어 큰 단점이 됩니다.
L2
L2 Loss는 연속적이고 미분 가능한 함수이기 때문에, 경량화 알고리즘에서 손실 함수를 쉽게 최적화할 수 있습니다. 제곱 오차를 사용하여 예측값과 실제값 간의 차이를 쉽게 이해할 수 있습니다.
하지만 큰 오차를 제곱하여 계산하므로, 데이터에 이상치가 포함된 경우 손실 값이 크게 증가합니다. 이상치에 대한 민감성 때문에 모델이 이상치의 영향을 많이 받을 수 있습니다. 즉, 작은 값에 대해서는 손실 값이 작은데 큰 값에서는 손실 값이 너무 커지는 문제가 있습니다.
위 두 손실함수를 합쳐 단점을 보완한 것이 Smooth L1 Loss입니다.
🔶 Smooth L1 Loss
L1 Loss의 장점인 이상치에 덜 민감한점, L2 Loss의 장점인 미분이 가능한 점을 합쳐 새로운 손실 함수를 만듭니다.
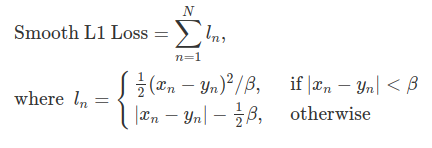
작은 오차에는 L2 Loss를 사용하여 미분이 가능하게 하였고, 큰 오차에는 L1 Loss를 사용하여 이상치에 덜 민감하도록 하였습니다. 베타 값이 커질수록 0 근처에서 V모양인 함수가 점점 부드러운 곡선을 그리게 됩니다. 또한 베타 값과 무관하게 기울기가 1에 가깝습니다.
