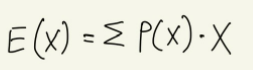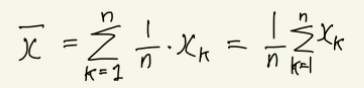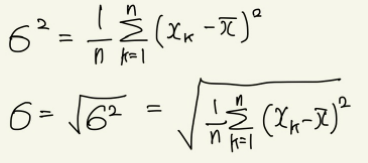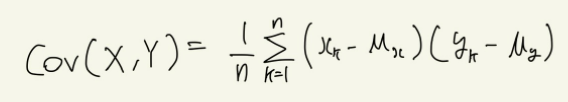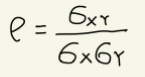확률과 통계는 '어떤 경향을 알아낸 후, 한정된 데이터로부터 전체의 모양을 예측'하기 위해 사용한다.

4-1. 확률

확률(Probability)는 어떤 사건이 우연히 발생할 가능성을 표현한 것으로, P를 사용하여 표현한다.

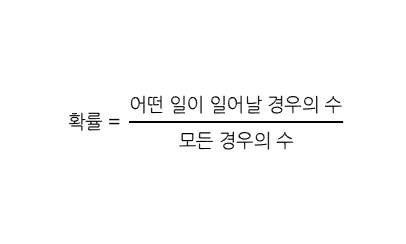
조합(combination): 서로 다른 n개로부터 중복 없이 k개를 골라내는 경우의 수

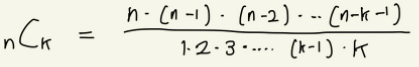
모든 경우에 대한 확률을 더하면 그 값은 1이 된다. 이를 이용하여 직접 구하기 어려운 확률도 간단히 구할 수 있다. 이때 사용하는 것이 '사건 A가 발생하지 않을 사건'이라는 의미로 사건 A의 여사건(complimentary event)를 사용한다.

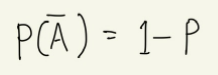
교집합: 사건 A와 사건 B가 동시에 발생하는 사건. A∩B (A and B)

• P(A∩B) = P(A)P(B)

합집합: 사건 A와 사건 B중에서 어느 한쪽이 발생할 사건. A∪B (A or B)

• P(A∪B) = P(A) + P(B) - P(A∩B)

현실 세계의 모든 현상들은 우연성을 가지기에 이런 현상을 표현할 때 확률을 사용하여 설명한다. 이때, 인공지능 분야에서는 상황을 판단하는 하나의 방법으로 정답이 될 확률이 가장 높은 것을 정답으로 채택하는 방법을 자주 사용한다.

4-2. 확률변수와 확률분포

어떤 변수 X를 P(X)의 확률로 나오게 할 수 있다면, 거꾸로 말해 어떤 변수 X를 사용할 때 확률 P(X)의 값을 구할 수 있다면 이 X는 확률변수(random variable)이라 말할 수 있다.

이산확률변수(discrete random variable): 확률변수 중 그 값이 연속되지 않고, 셀 수 있게 뿔뿔히 흩어진 값을 가짐. 어떤 사건이 일어나는 시행 횟수와 같이 뿔뿔히 흩어진 값들.

• 이산확률분포: 확률변수의 값이 달라질 때 확률도 달라지는데, 이렇게 이산확률변수의 값에 따라 달라지는 확률들을 전체적으로 정리하여 나열한 것.

• P(X)=f(X) 어떤 사건의 이산확률변수가 X일 때, 그에 대한 확률 P는 이산확률분포 f(X)를 따른다.

• 주사위 두 개를 던졌을 때 숫자의 합을 확률변수 X라고 할 때, 확률분포 f(x)는 다음과 같다.

• 이를 보면 삼각형 모양으로 확률이 분포한다는 것을 알 수 있는데, 이 상황에서 주사위 개수를 늘려가면 이 이산확률분포는 점점 더 종형곡선(bell curve)의 모형에 가까워지며, 시행(trial)을 무한 번 하는 극한에서는 이러한 종형곡선을 정규분포(Normal distribution)라고 한다.

연속확률변수(continuous random variable): 값이 특정 범위 내에서 실수 형태로 존재하여 소수점 이하까지 내려가는 값을 가짐. 경과 시간과 같이 끊김이 없이 연속적으로 이어지는 값들.

• 어떤 사건의 연속확률변수가 X일 때, 그에 대한 확률 P는 연속확률분포 P(x)를 지정한 X의 구간 안에서 적분한 값과 같다.

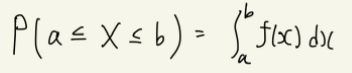
• 어떠한 연속확률분포 f(x)=P(H)를 가정했을 때, 확률변수 H는 연속확률변수이기 때문에 어떤 실수값이든 가질 수 있다. 예를 들어 성인 남성의 키가 H=173이 되는 확률을 구하고자 할때, H=173이라고 말하더라도 엄멀히 따지면 173.01이거나 173.00000001, 172.999999가 될 수도 있다. 즉, H는 연속적이면서도 얼마든지 더 세밀한 값을 지정할 수 있기에, H=173이라고 딱 잡아서 얘기할 수 없다. 이에 어떠한 구간을 설정해 주어야 H가 그 구간 안에 있는지 아닌지를 알 수 있고, 그에 대한 확률 P(H_도 정의할 수 있다.

즉, 이산확률변수나 이산확률분포는 한정된 횟수로 시행을 반복할 때 나오는 확률이나 그것들의 분포를 표현할 때 사용한다. 이에 우리가 주변에서 흔히 '확률'이라고 생각 하는 것이 이들이다.

그러나 연속확률변수나 연속확률분포는 앞에서 예를 든 것처럼 하나의 값으로 지정할 수 없다. 이때 연속확률분포에는 다양한 종류가 있다. 어떤 이산확률분포도 무한번 반복하다 보면 대부분 이러한 연속확률분포 중의 한 형태로 수렴하게 된다.

즉, '이 확률은 이러한 확률분포를 따른다'라고 가정하고, 그 가정이 대체로 무난하게 맞아 들어가기만 하면 비교적 적은 수의 시행만으로도 무한 번 시행한 것 같은 확률의 분포를 추측해 낼 수 있다. 이렇게 적은 정보를 가지고 어떤 경향을 추측하는 것이 바로 '통계'이다.

어떤 현상에 대해 관측 결과들을 이산확률변수로 취급하고, 이에 대한 이산확률분포를 구할 수 있다면, 다음에 일어날 사건에 대한 확률을 과거의 데이터로부터 추측할 수 있다. 또한 적절한 연속확률분포를 선택한다면 적은 수의 시행만으로도 앞으로 일어날 사건의 확률을 추측할 수 있다.

4-3. 결합확률과 조건부확률

결합확률 공식: 사건 A와 사건 B가 서로 독립된 사건일 경우, 사건 A, B가 동시에 일어날 확률

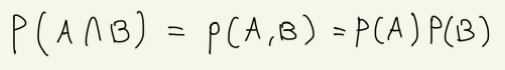
조건부 공식: 사건 B가 일어난다는 것을 전제로 한 사건 A가 일어날 확률

백반 명 중 다섯 명 꼴로 걸리는 어떠한 질병을 진단하는 데 AI기술을 사용하면 99.99%의 정밀도로 그 사람이 질병에 걸렸는지 안 걸렸는지를 판정할 수 있을 경우, A씨가 이를 받았을 때 진단 결과가 양성이라면, 실제로 최수정씨가 이 질병에 걸렸을 확률은 얼마일까.

• '검사결과가 양성이고, AI 진단의 정밀도가 99.99%라면 실제 환자일 확률은 99.99%이다.'라는 말은 틀린 것. 조건부확률(AI가 양성이라 판정한 후 실제로 질병에 걸렸을 확률)과 결합확률(AI가 양성이라 판정했고 실제로 질병에 걸렸을 확률)을 구분하지 못한 것.

• 사건 A: 실제로 질병에 걸린 환자다. ( P(A) = 0.000005 )
  사건 B: AI가 잘못된 판정을 했다. ( P(B) = 0.0001 )
  사건 C: AI가 양성으로 판정했다.

• 다음과 같이 사건을 정리할 수 있으며, 최종적으로 원하는 것은 'AI가 양성으로 판정한 후, 실제로 병에 걸렸을 확률'을 구하는 것이므로, P(A|C)를 풀어야 한다. 이 식에는 'AI가 실수로 양성으로 판정한 후' 라는 조건까지 포함하고 있다. P(A|C)를 구하기 위해서는 다음과 같은 식이 필요하다.

• P(A∩C)는 'AI가 양성으로 판정했고, 실제로 병에 걸렸을 확률'. 즉, '실제로 병에 걸렸고, AI도 정확하게 판정한 것'으로 말할 수 있다.

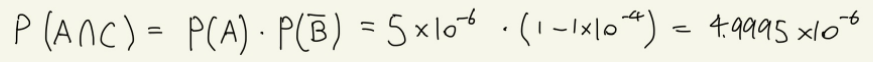
• P(C)는 '실제로 병에 걸렸고, AI도 정확하게 판정했다'라는 경우와, '실제로 병에 걸리지 않았고, AI가 잘못된 결과를 냈다'라는 두 가지 상황으로 나뉜다.

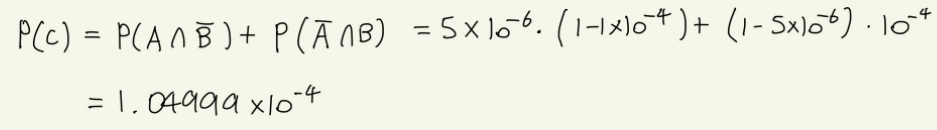
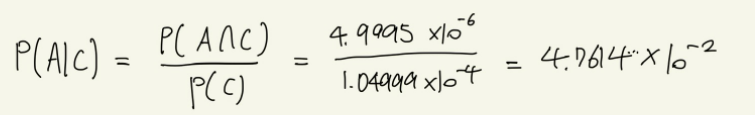
결론적으로 AI 검사 결과가 양성이라 하더라도 A씨가 실제로 질병에 걸렸을 확률은 4.76%이다.

예측 모델의 정밀도나 정확성을 표현할 때는 다양한 방법으로 평가할 수 있기 때문에 사용하려는 목적에 따라 지표를 잘 선택해서 사용할 필요가 있다. 이때 인공지능 모델의 정확성을 표현할 때 사용하는 대표적인 지표로는 정밀도(precision)과 재현율(recall), F값 등이 있다.

4-4. 기댓값

기댓값: 나올 것이라고 예상하는 값. X가 확률변수이고 확률 P(X)인 사건이 벌어질 때, 예상할 수 있는 결과값을 기댓값이라고 한다.

모든 이산확률변수 X에 대한 기댓값 E(X)는 다음과 같다. (이때, 확률은 P(X))

4-5. 평균과 분산, 공분산

평균은 수학적으로 확률에서 말하는 기댓값과 같은 의미.
'과거 6개 월간의 매출 평균이 다음 달의 예상 매출액이 된다'라고 하는 것을 확률의 관점에서 달리 표현하면 '6개의 확률변수(각 달의 매출액)이 각각 같은 확률(1/6)로 발생하므로, 다음 한 달 동안의 매출에 대한 기댓값은 각 월의 매출에 1/6을 곱한 것을 모두 더한 것과 같다.'라고 표현 가능.

n 개의 확률변수가 각각 x1, x2, x3, ..., xn이라는 값을 가질 때 평균값은 다음과 같다.

그러나 사실 이렇게 평균값을 구한다고, 다음 달의 매출을 올바르게 에상할 수 있는 것은 아니다. 매번 다른 패턴으로 매출이 발생하기 때문. 이에 평균값과 데이터가 얼마나 차이가 나는지 표현하는 방법인 편차(deviation)역시 알아야 한다. 편차의 관점에서 보면 매달 얼마만큼의 매출액이 고객별로 흩어져 있는지를 알 수 있다. 이때, 편차의 합계를 구하면 0이 되기에 단순히 편차를 구해서 합치는 것만으로는 매출의 흩어진 정도를 확인할 수 없다.

이에 분산(variance)라는 개념이 필요하다. 분산은 편차를 제곱한 다음 합계를 구하고, 이를 다시 평균값으로 만든 것. 이때, 분산은 제곱한 값이기 때문에 단위를 표현하기가 애매해지는데, 이때 본래의 의미를 되찾기 위하여 제곱근을 이용한다. 이렇게 분산에 제곱근을 씌운 값을 표준편차(standard deviation)이라고 한다.

n 개의 확률변수가 각각 x1, x2, x3, ..., xn이라는 값을 가지고, 평균값이 x̄일 때 분산 σ²과 σ는 다음과 같다.

이들을 이용하여 데이터가 얼마나 흩어져 있는지, 얼마나 차이가 심한지를 알 수 있어 데이터의 경향을 표현할 때 사용한다.

두 확률변수 사이에 정의된 공분산(covariance)은 두 확률변수의 선형관계, 즉 상관관계에 대한 정보를 알려준다. 이를 이용하려면 우선 두 가지 데이터를 결정해야 한다. 또한 공분산 애당초 서로 다른 두 데이터 간의 관계를 표현하는 지표이기에 계산 과정에서단위에 대해 신경쓸 필요가 없다.

두 가지 데이터에 대한 n조의 확률변수 (X, Y) = {(x1,y1), (x2,y2), ..., (xn,yn)}이 있다고 가정했을 때, X의 평균이 μx이고, Y의 평균이 μy일 때, 공분산 Cov(X, Y)는 다음과 같다.

이때, 공분산의 절댓값이 크다고 해서 양의 관계나 음의 관계의 강도가 더 세다고 말할 수는 없다. 양의 관계나 음의 관계의 강도는 상관계수로 비교할 수 있다.

4-6. 상관계수

공분산(Cov)는 서로 다른 두 확률변수의 관계를 표현하는 지표이기에, 단위 등에서 차이가 발생하여 서로 다른 공분산들은 비교할 수 없다. 그러나 상관계수를 이용하면 관계의 강도를 비교할 수 있다.

확률변수 X와 Y의 분산이 양수이고 각각의 표준편차가 σx, σy, 공분산이 σxy라고 할 때, 상관계수는 다음과 같다. 이때, -1 ≤ ρ ≤ 1

상관계수 ρ는 공분산을 각각의 표준편차로 나누어 단위를 없애버린 값으로, 단위가 없는 무차원수이다. 공분산을 표준편차의 곱으로 나누게 되는 정규화 과정을 거치면서, -1과 1 사이의 값을 가지게 된다.이제 이를 이용한다면, 상관관계의 강약을 비교할 수 있다. 상관계수는 일반적으로 절대값이0.7보다 클 때 상관관계가 강하다고 말한다.

사람이 직관적으로 분석하기 어려울 만큼의 데이터가 있다면, 컴퓨터로 하여금 수 많은 파라미터를 조합하고, 그들의 상관계수를 계산하면서, 상관관계가 강한 조합을 찾아낼 수 있습니다. 이를 이용하면 사람이 미처 발견하지 못했던 숨은 관계나 데이터의 특징을 찾을 수 있다.

4-7. 최대가능도추정

우리는 어떤 사건의 확률을 알기 위해서는 몇 번이고 시행을 반복하면서, 그 과정에서 얻은 관측 결과를 통해 추정을 해봐야 한다. 이에 통계적인 추정 방법인 최대가능도추정(Maximum likelihood estimation)을 사용해야 한다. 이는 '가장 그럴듯하게 값을 추정'한다는 의미. 이는 곧 파라미터 θ에 대하여 가능도함수 L(θ)를 최대화 할 수 있는 θ값을 구하는 것을 의미한다. 이때 최댓값을 구하는 지점은 한 번 미분을 했을 때 dL(θ)/dθ=0이 되는 지점이고, 이 지점에서의 θ를 구하면 되는 것이다.

주사위를 던졌을 때 숫자 1이 나올 확률은 1/6이라고 알고 있지만, 그렇게 단언할 수는 없기 때문에 그 확률을 θ라고 하자. 이에 주사위를 100번 던져서 20번 숫자 1이 나왔다고 하자. 경우의 수는 다음과 같으며, 이렇게 관찰 결과가 발생할 확률을 가능도함수(L(θ))라고 한다.

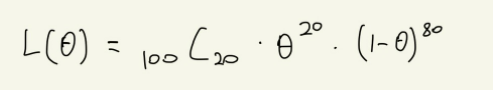
관찰결과로 이러한 식을 구할 수 있으나, 이를 미분하려면 상당히 복잡할 것이다. 이에 자연로그를 붙여 로그가능도함수를 만들어 준다. 로그를 붙여준다면 곱셈을 덧셈으로 바꿀 수 있기 때문이다. 가능도함수 L(θ)를 최대로 하는 θ는 로그가능도함수 logL(θ)에 대해 다음 방정식을 만족한다.

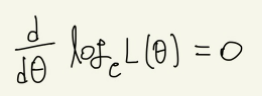
이를 통하여 위의 식을 계산하면 아래와 같이 편하게 계산할 수 있다.

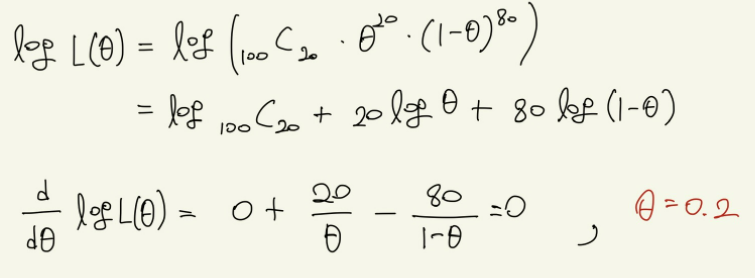
정규분포와 같은 연속확률분포에서는 파라미터가 여러 개인 경우도 있다. 이때는 각 파라미터에 대해 편미분을 하면 된다.

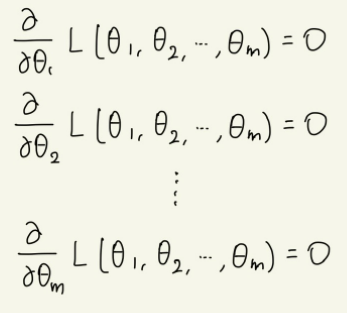
이산확률분포와 연속확률분포 둘 다 가능도함수로 사용할 수 있고, 파라미터가 여러 개라 하더라도 괜찮다.

그러나 가장 문제가 되는 것은 '수집한 데이터(사건 관찰 결과)'를 확률분포가 얼마나 잘 표현하는가이다. 보통 일반적인 경우라면 정규분포를 사용하지만, 추정하려는 사건을 잘 이해한 후, 적절한 확률분포를 적용해야 한다.

인공지능에서 최대가능도추정은 이미 확보한 데이터를 사용해서 미처 발견하지 못한 확률 모델의 파라미터를 추정할 때 사용하는 통계 기법이다. 실제로 과거로 데이터로부터 미래를 예측할 때 이를 많이 사용한다.

수학적으로 정확한 최대가능도추정법 VS 실용적이지만 의심스러운 베이즈 추정법

최대가능도 추정법의 접근 방식은 '진정한 확률 모델은 존재하며 관찰된 데이터는 그러한 모델을 충실히 따르고 있다. 따라서 시행을 반복하면서 결과를 평균을 내다 보면 진정한 확률 모델이 보이기 시작할 것이다. 다만, 시행을 무한히 할 수는 없기에 지금 당장 얻을 수 있는 데이터로부터 가장 그럴듯한 확률을 이끌어낼 수밖에 없다. 즉, 관찰되는 데이터를 믿을 수밖에 없다.' 라는 것, 이에 관찰 결과에 영향을 많이 받는데, 어쩌다가 관찰 결과가 한 쪽으로 치우치거나 부적절한 확률분포를 적용해 버리면 완전히 엉뚱한 추정 결과가 나오는 약점이 있다.

이러한 약점을 보완하기 위한 방법으로 베이즈 추정법이 있다. 이는 지금까지의 관찰 결과를 근거로 '사전분포(확률)'을 가정한다. 이후 '관찰을 통해 얻은 데이터는 사전분포에 따라 얻어진 결과이므로, 그에 대한 조건부확률을 구하면 된다'라는 접근 방법으로 '사후확률(조건부확률)'을 구한다.

그러나 통계에서는 모든 한계들을 명확히 인지한 상태에서 데이터를 다루려는 자세가 중요하다.