Multivariate Data Analysis 2. Multiple Linear Regression, Pilsung Kang 강의를 참고하였습니다.

https://www.youtube.com/watch?v=NknX91JdVA0&list=PLetSlH8YjIfWKLpMp-r6enJvnk6L93wz2&index=5

1. Multiple Linear Regression

다양한 변수들이 존재하지만, 우리가 찾고자 하는 것은 Price이므로, 이를 Y로 설정. 다른 변수들을 X로 설정하고, Y=f(X)를 만족하는 f를 찾기 위해 다중회귀분석 모형을 사용하겠다는 것!

이때 X들을 Independent variables(attributes, features)라고 하고, Y를 Dependent variable(target)이라고 한다.

다중회귀분석의 목적은 정량적인 목적변수인 Y와 여러 가지의 설명변수 X들 사이의 선형 관계식을 찾는 것이 목적

Regression의 의미는 Y가 실수값이라는 것(Y∈R). Clssification은 Y가 유한함.

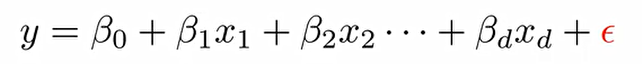
종속변수 y는 설명변수 x들에 대한 1차 항들의 결합. 결합 계수들인 β들은 이미 정의가 되어 있는 것.

이때 가장 중요한 것은 노이즈를 의미하는 ε. 이는 시스템이나 사람이 어찌할수 없는 변동성을 의미한다. 우리가 수집하는 대부분의 데이터에는 어쩔 수 없이 대부분 존재한다.

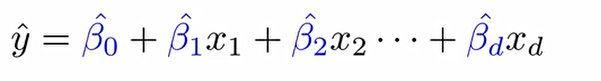
이에 우리는, 다중선형회귀분석을 통하여 충분히 많은 x와 y에 대한 조합들이 주어 졌을때 설명변수들과 종속변수들 관계를 맺어주는 파란색의 β를 찾는 것이 목적. 회귀 계수(coefficients)는 찾는 것.

다중선형회귀분석은 다음과 같은 두 가지 형태로 나타낼 수 있다.

1. Explanatory Regression(설명적 회귀분석)

• 설명변수와 종속변수와의 관계를 설명하는 것!
• 목적: 데이터를 잘 fitting하여, 설명변수가 종속변수에 얼마나 큰 영향을 미치는지 파악하는 것.
• 지표: R^2
• 분석대상: β. 이들이 얼마나 적합하게 추정이 되었는가. 이때 설명변수들은 얼마나 영향이 있는가.

2. Predictive Regression

• 과거 데이터로부터 회귀 모형을 만든 후, 미래 y값은 모르고 x값만을 알 때, 이 x값들로 y값을 얼마나 잘 예측할 수 있는가?
• 목적: 새로운 데이터에 대해서 예측력을 극대화 하는 것
• 분석대상: Y

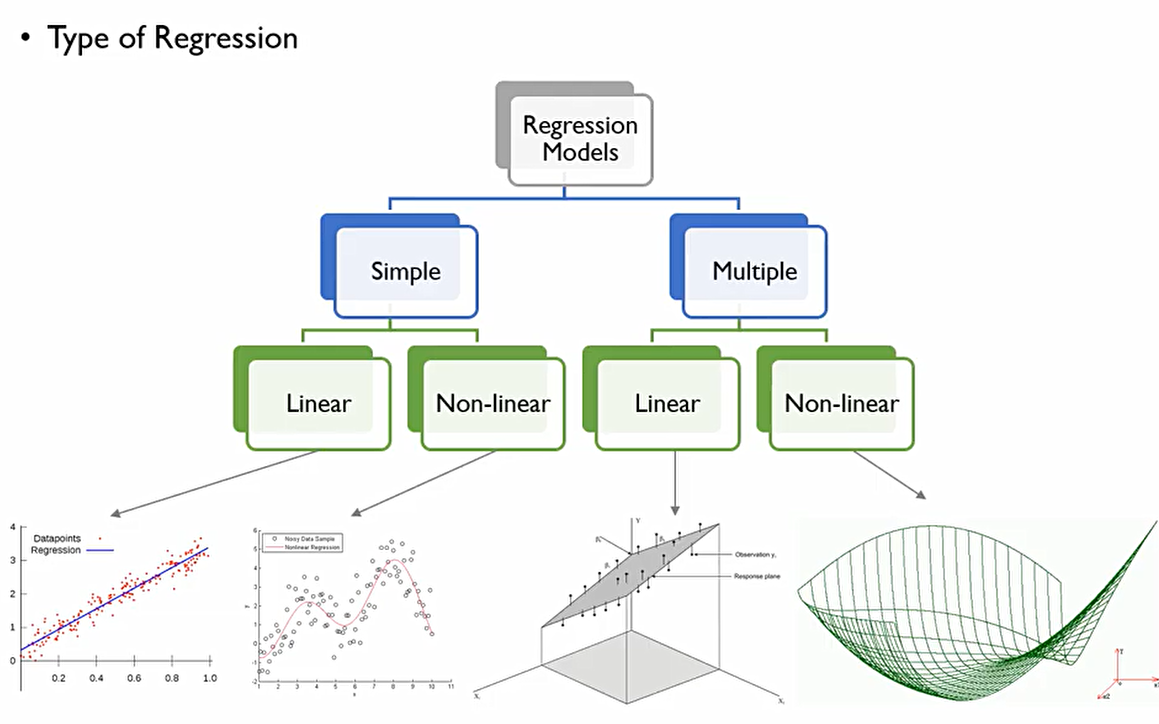
회귀모형의 Type은 다음과 같이 나눌 수 있다.

Simple과 Multiple의 기준은 얼마나 많은 x가 존재하는 것인가.

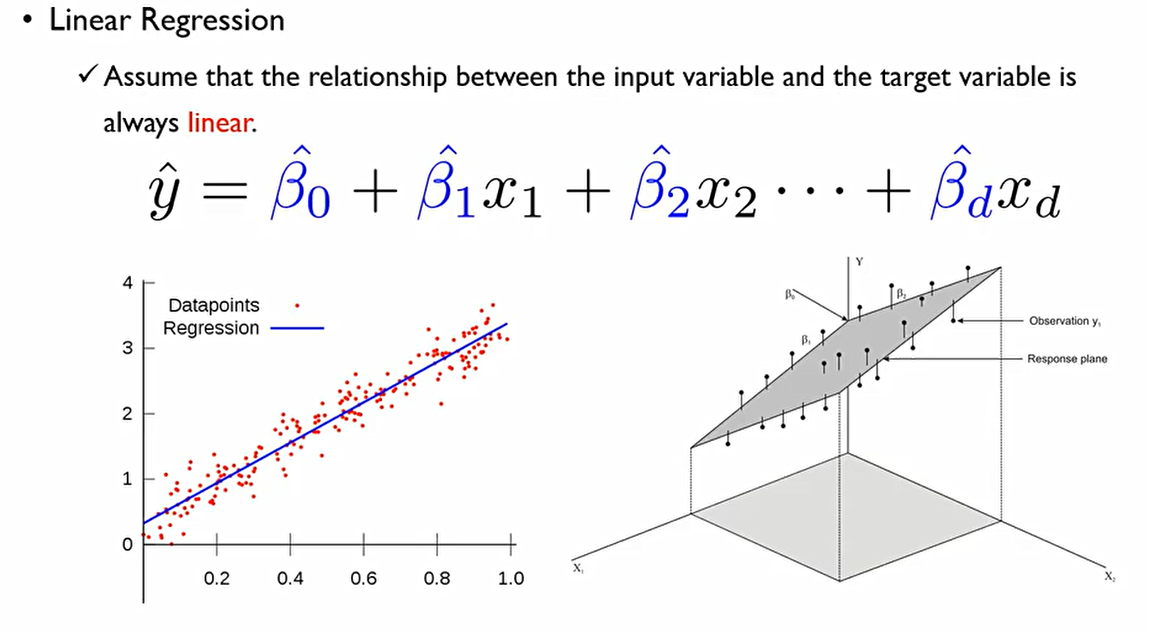
선형회귀분석의 가장 기본적인 가정(Assume)은 데이터가 선형식으로부터 생성이 되는지 아닌지 사실은 모르지만, 설명 변수(input variable)과 종속변수target variable사이에는 항상 linear관계가 성립한다는 것. 즉, 1차항의 결합으로 표현될 수 있다. 이에 일차항의 결합에 대응하는 β를 찾는 것이 목적

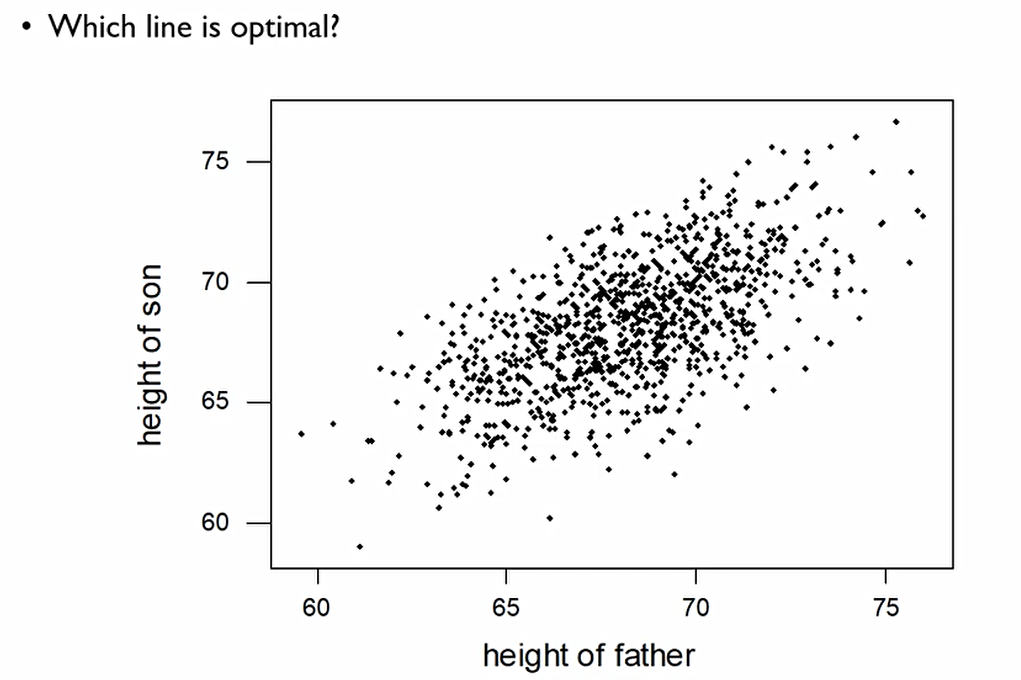
이는 아빠의 키가 아들에 키에 어떤 영향을 미치는 지 나타내는 분포표

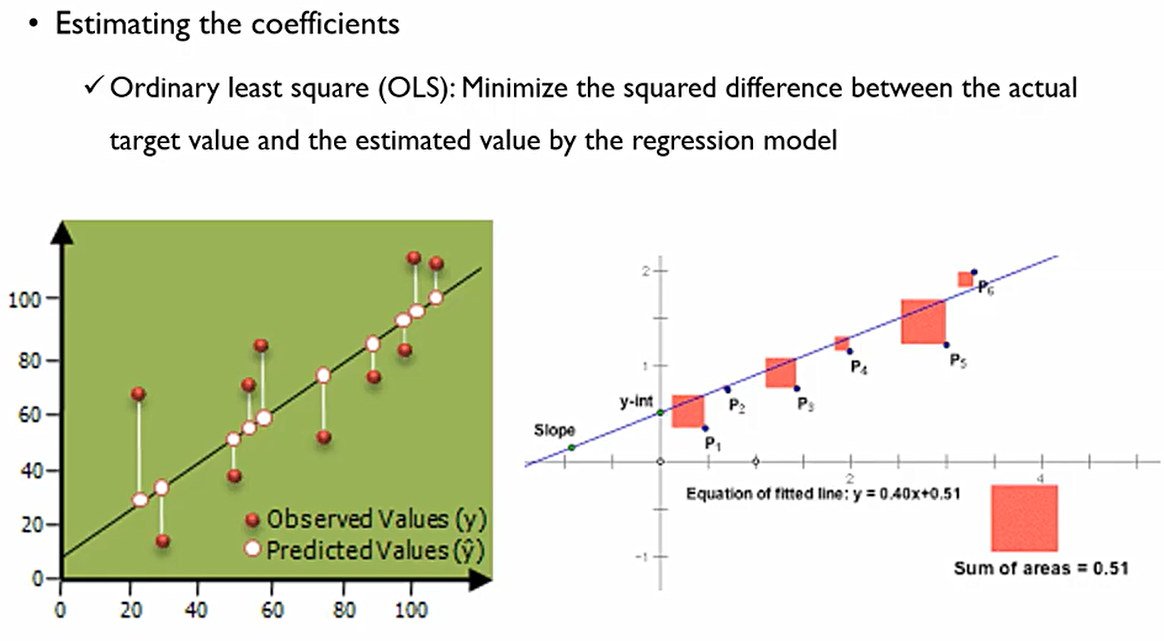
그렇다면 β^hat들을 어떻게 구할 수 있을까? 이를 위해서 최소자승법(Ordinary least square(OLS))를 대표적으로 이용한다. 실제 Target의 값과 회귀식에 의해 추정된 값의 square difference를 최소화 하는 직선을 찾겠다는 것.

왼쪽의 그래프에서 흰색 선은 실제값과 추정된 값의 차이(y-y^hat)인데, 두번째 처럼 음수의 경우를 제외하기 위하여 절댓값이나 제곱값 중 제곱을 씌워주는 방식으로 이를 없애는 것.

즉, 위에서 나타내는 것을 식으로 표한하면 다음과 같다. n은 관측치의 개수.

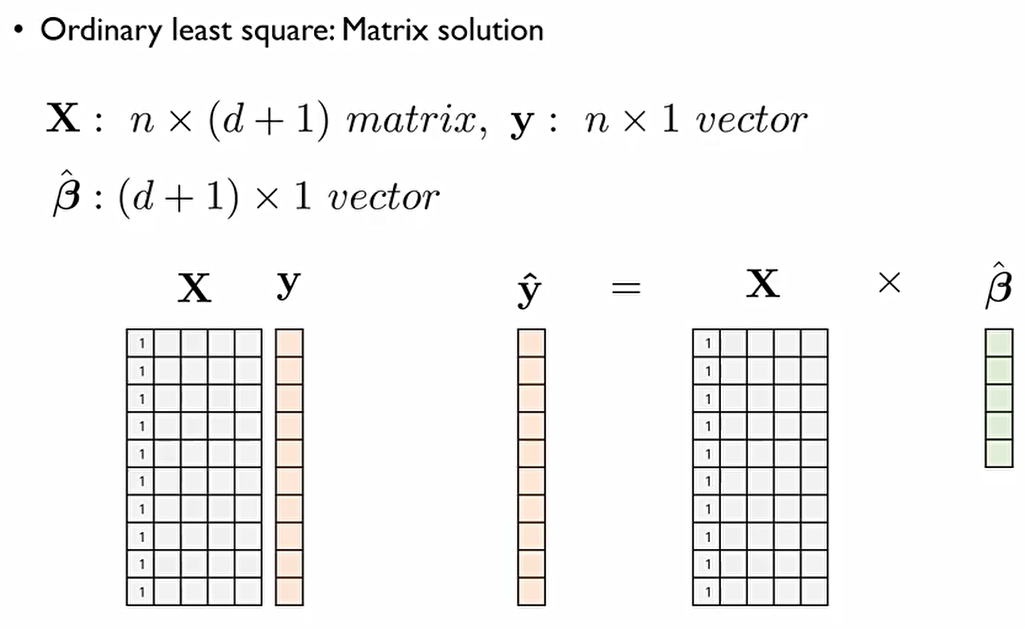
n개의 관측치에 대하여 영향을 미치는 변수가 d개 있다고 할때, 다음과 같이 나타낼 수 있다.

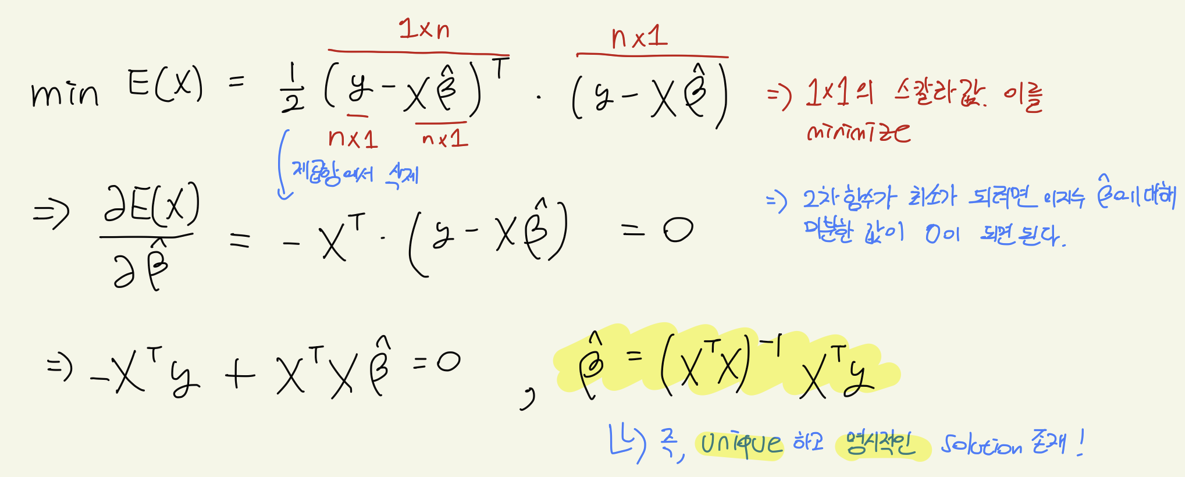
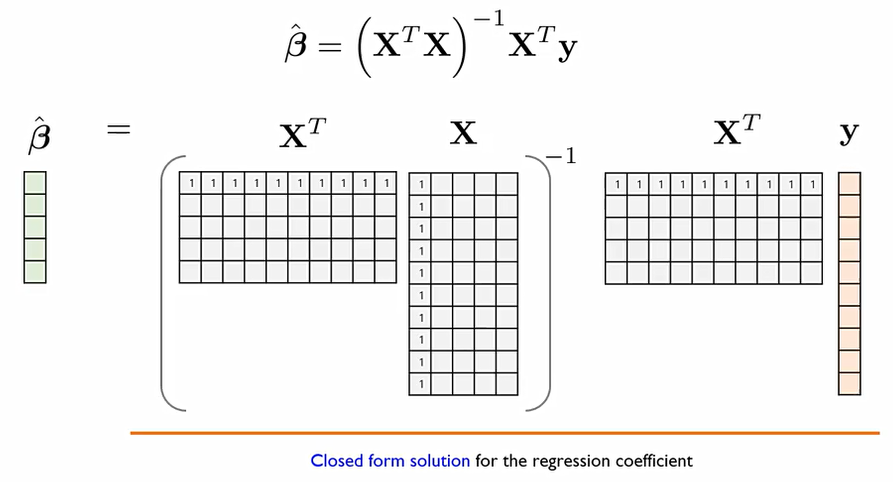
즉, β^hat이라는 closed form solution을 가질 수 있다.

통계에서 개발된 알고리즘이기에, β라는 추정값이 Best라고 말하기 위해서는 다음 조건들이 충족되어야 한다.

• 노이즈 ε는 Normal distribution을 따라야 한다.: 데이터로 검증가능

• 선형관계가 맞아야 한다.: 머신러닝에서 문제를 가짐. 문제가 정말 선형식인지는 데이터를 생성하는 메커니즘이 주어지지 않는 한 현실세계에서는 알 수 없다. 이에 엄격히 검증하지 않음.

• case(관측치)들이 서로에 대해서 독립적이어야 한다.: 머신러닝에서 문제점. 이 가정이 무너지는 경우가 많다.

• Y의 변동성이 특정 다른 변수에 영향을 받지 말아야 한다. (homoskedasticity): 데이터로 검증가능

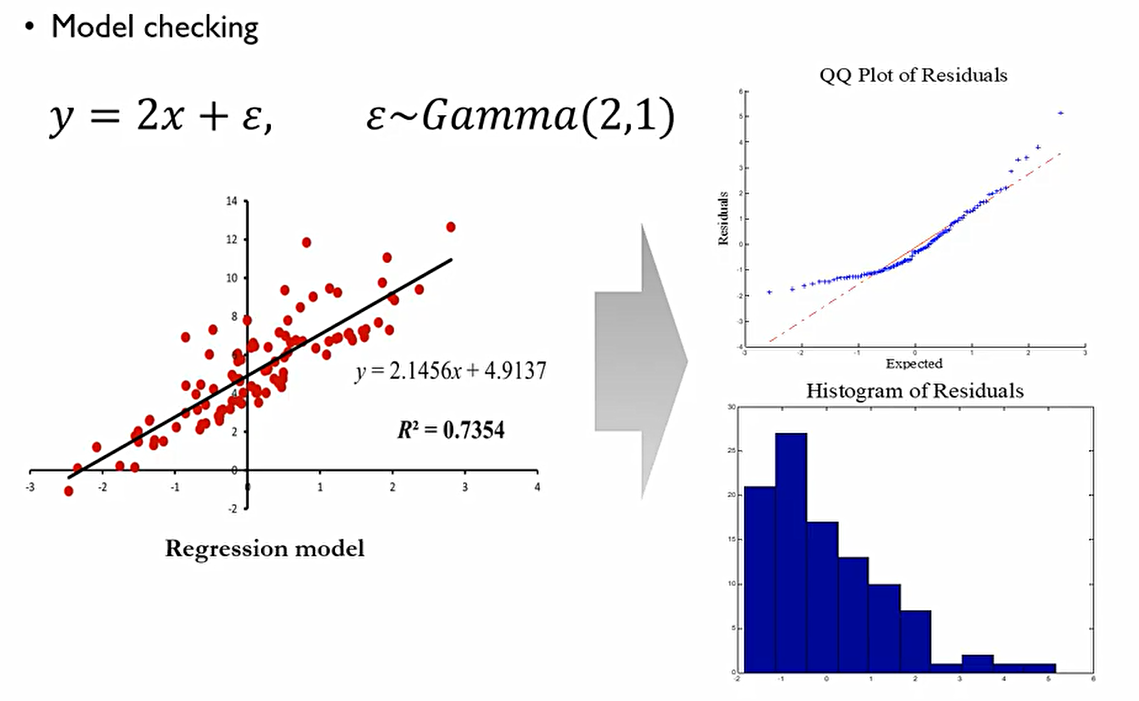
노이즈 ε는 Normal distribution을 따라야 한다.의 내용. 이때 잔차(residual)들의 QQplot을 그리면 다음과 같다. 이때 선에 따닥따닥 점들이 붙어있지 못하므로 잔차에 대한 정규성을 담보할 수 없다. 이러면 사용되는 회귀식을 사용할 수 없다.

QQPlot: 정규분포를 가정했을 때의 순위를 x축으로, 실제 데이터가 가지는 값을 y축으로 놓았을 때 다음 선을 모든 점들이 붙어있어야 정규성 검증이 이루어질 수 있다.

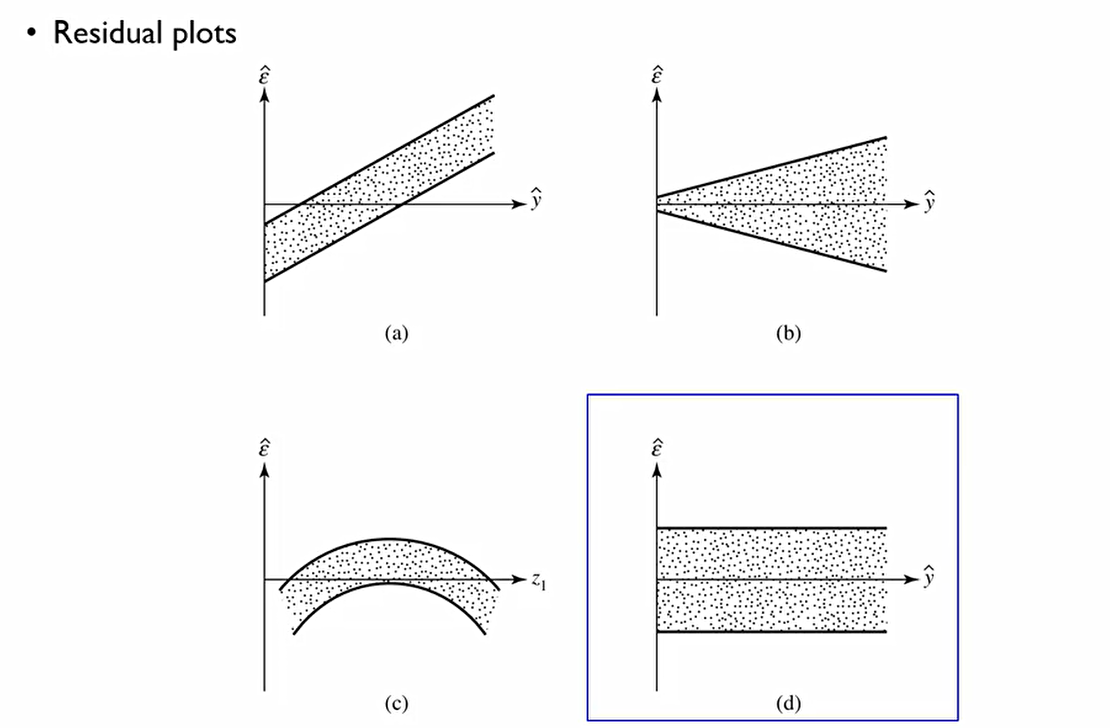
Y의 변동성이 특정 다른 변수에 영향을 받지 말아야 한다. (homoskedasticity)의 내용. 이때 ε^hat은 y-y^hat을 의미하는데, 이때 4번째와 같이 변동성이 일정한 그림이 나와야 한다.

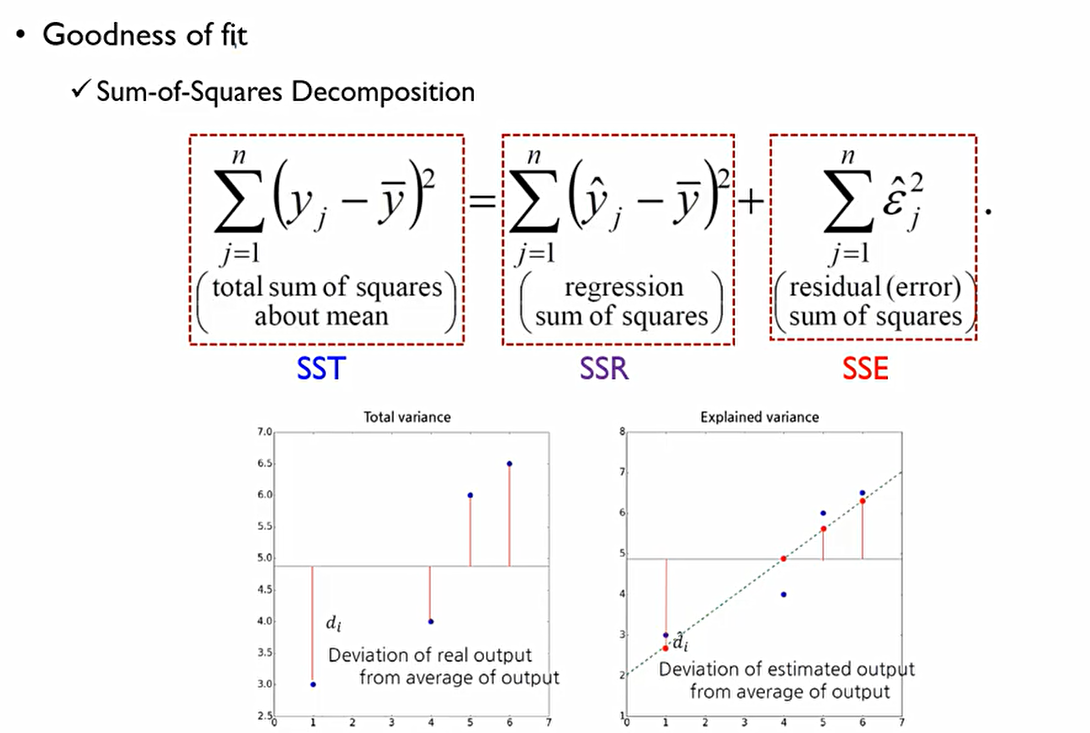
Goodness of fit은 회귀모델이 얼마나 주어진 데이터를 잘 설명했냐를 측정하는 척도.

OLS의 관점에서 SSE는 회귀식에서 설명할 수 없는 변동성이므로 이를 최대한 작게하는 것이 목적. 이때 SST(TSS)값은 항상 동일하므로 SSR(회귀식에 의해 설명되는 변동성)값을 최대한 크게할 수 있어야 한다.

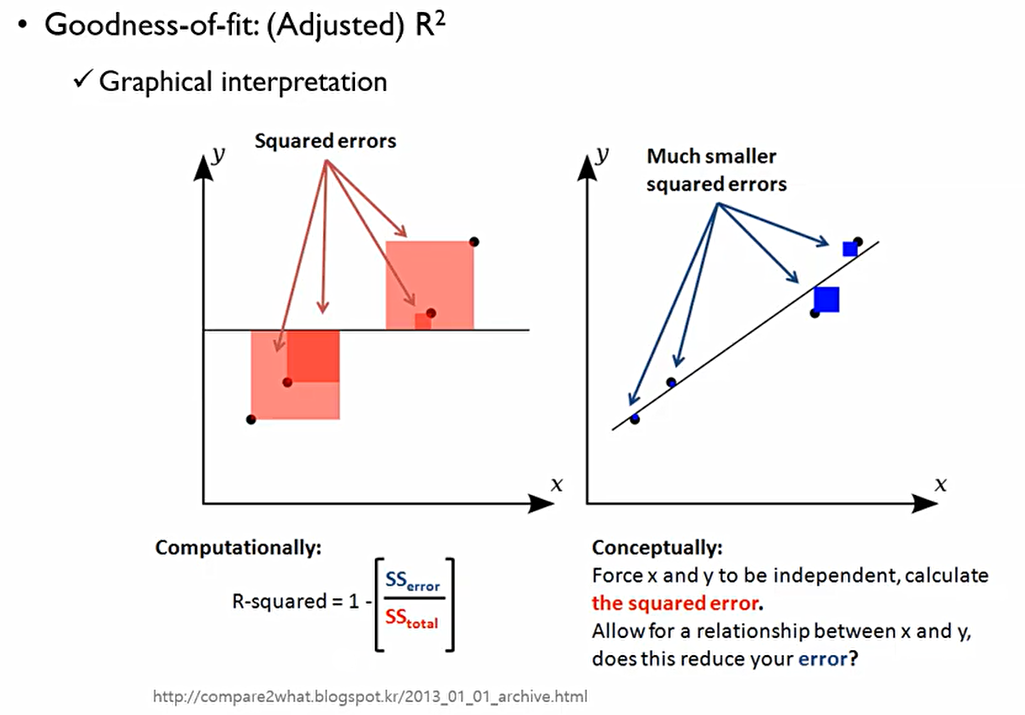
R^2는 1-(SSE/SST)이다. 즉, 전체 변동성 중에서 회귀식에 의해 설명되지 않는 변동성을 1로 빼주는것. 즉 SSR/SST와 동일하다.

그림에서 SST는 빨간 정사각형이고, SSE는 파란색 정사각형. 즉, 빨간색 정사각형 대비 파란색 정사각형이 작아야 한다.

이에 R^2는 0과 1사이에 값을 가진다.

R^2 = 1의 의미는 가지는 데이터의 변동성을 회귀모형이 전부 설명할 수 있다는 뜻. 완벽한 선형관계를 가짐.

R^2 = 0의 의미는 설명변수와 종속변수에는 아무런 선형 관계가 없다는 것. 이때 중요한 점은 관계가 없는 것이 아닌 선형 관계가 없다는 것

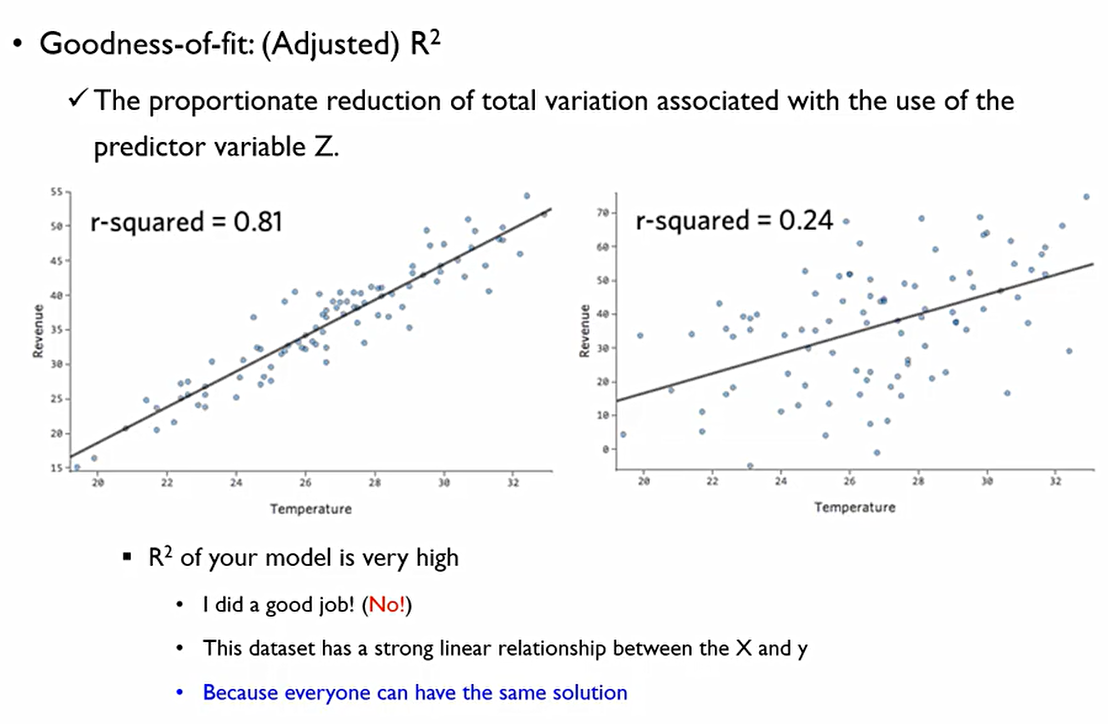
R^2는 데이터 분석가의 역량에 좌우되는 값이 아니다. 데이터 자체가 가지는 속성에 의해 좌우되는 값.

즉, R^2값이 높다라는 것은 내가 잘 분석한 것이 아닌, x와 y가 강한 선형관계를 가지고 있다는 것.

R^2가 가지는 가장 큰 단점 중 하나는 변수수가 증가하면 R^2는 단조증가를 해버린다는 것. 즉, 변수의 질을 떠나 변수의 개수가 많을수록 R^2는 커지게 되어버린다. 이에 Adjusted R^2를 사용한다.

위의 식에서 p는 변수의 수를 의미한다.

최종적으로, 모델이 잘 설정되었는가를 보기 위해서는 Adjusted R^2를 보고, 또한 Residuals이 독립적인지, 정규분포를 따르는지 체크해야 한다.

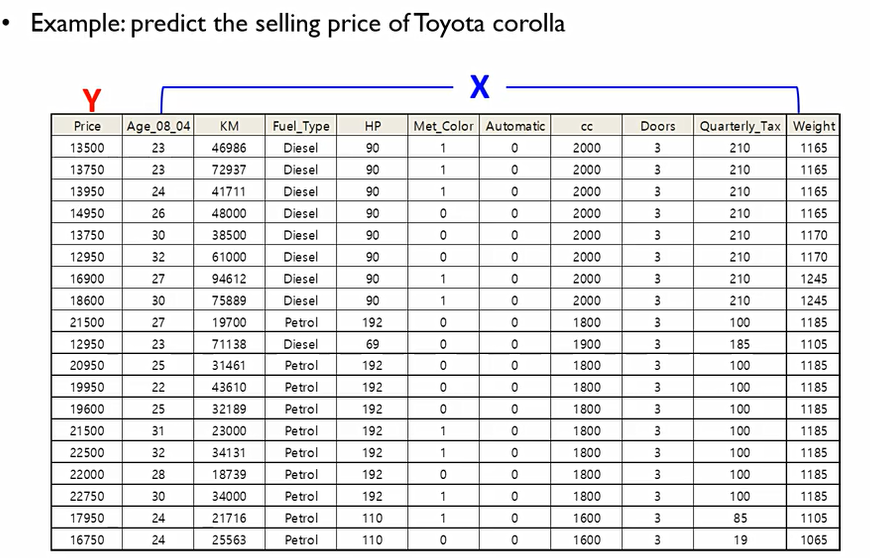
다음의 예시에서 Fuel_Type을 보면 형태가 명목형 변수로 되어있다. 이를 다음과 같이 dummy변수로 만들어서 one-hot encoding을 해준다.

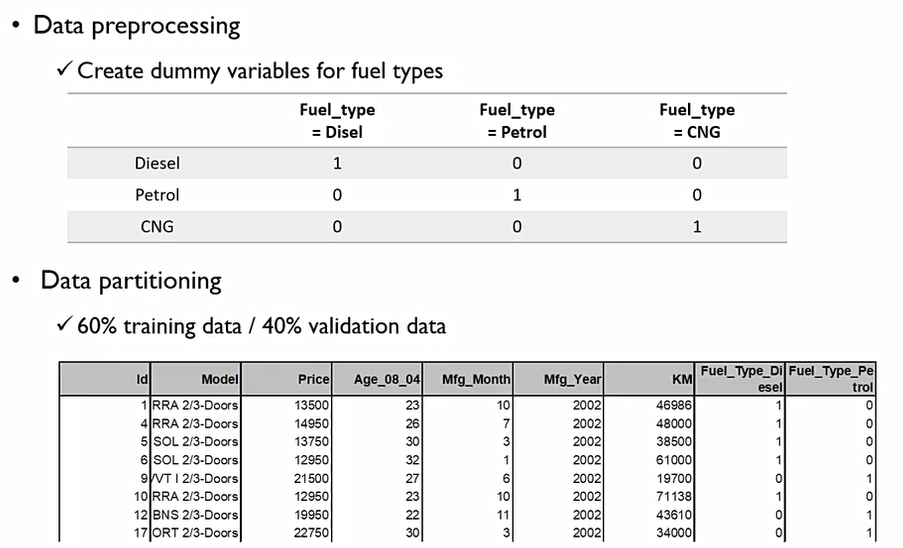
이때 이렇게 하는 이유는 명목형 변수의 특징 때문인데, 두 서로 다른 값은 다를 뿐이지, 다름의 차이는 없기 때문이다.

**즉, |D-P| = |P-C| = |C-D|

이에 D, P, C를 각자 1, 2, 3등으로 놓는 변수화 방법은 적절하지 않다.

또한, 다중회귀분석을 진행할때 C=1-A-B가 되어버리는 경우가 있어, 아래처럼 one-hot encoding을 진행하기도 한다.

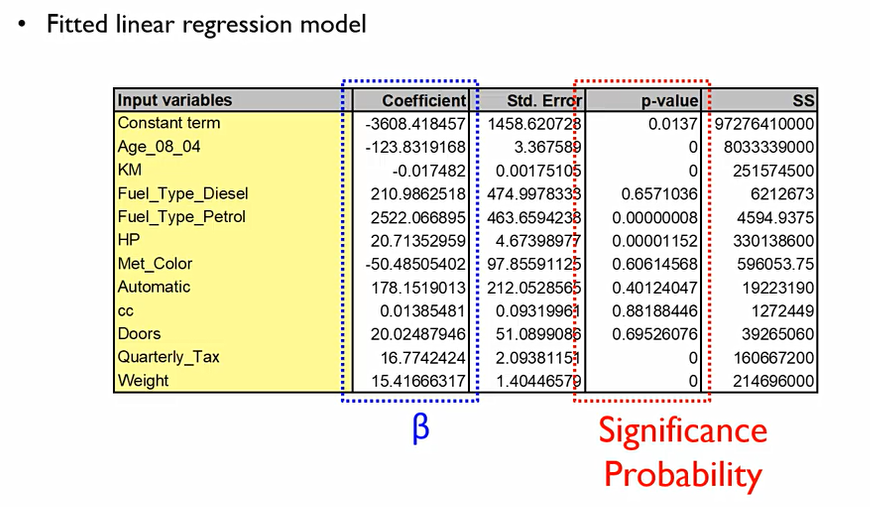
회귀모형을 만든 후, 두 가지의 눈 여겨봐야하는 파트가 존재한다.

• coefficient: 회귀계수로, 1만큼 증가할때 종속변수가 증가하는 단위.

• p-value:
  null hypothesis는 다음과 같고
  
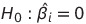
  alternative hypothesis는 다음과 같은데,
  

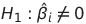
이때 p-value가 0에 가까울 수록 alternative hypothesis와 같으므로 해당 변수는 중고차 가격에 중요한 영향을 미친다고 볼 수 있다. 1에 가까울수록 통계적으로 유의미하지 않을 수 있다.

결론적으로, coefficient가 모델링에 유의미한지 보기 위해서는, p-value를 먼저 확인해야 한다.

2. Evaluation Regression Models

회귀모형이 우수한지 아닌지를 어떻게 판별할 수 있을까? 이를 위한 평가 지표가 존재한다.

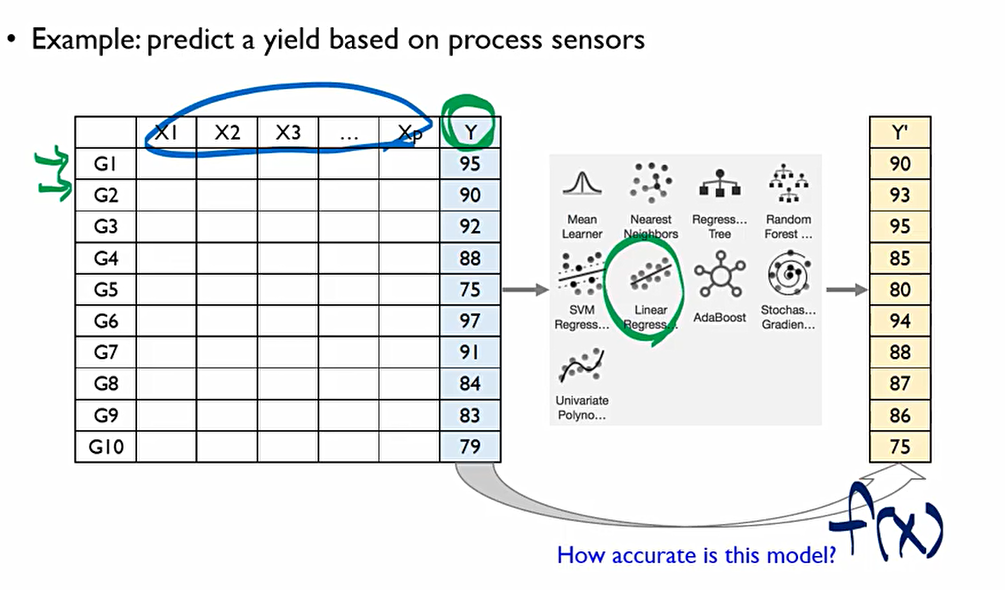
G 들은 관측치, x 들은 변수들을 y는 최종적인 성과물 Output. 즉 y를 예측하기 위하여 x들을 바탕으로 어떠한 회귀모형을 만들었을 때 y'=f(x)의 값이 나왔다.

그렇다면, 이때 이 모델의 예측값 y'=f(x)는 얼마나 정확할까? 이를 정량적으로 표시할 수 있는 지표가 있다.

1. Average Error(평균 오차): 모델의 실제값 y와 예측된 y'의 차이에 대한 평균을 산출하는 measure.

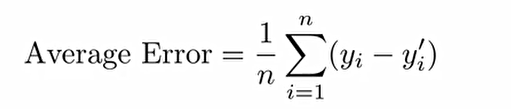
그러나 사실 Sign(부호)때문에 measure의 효과를 잘못 이끌어낼 수 있기에 사실 지금은 사용해서는 적절하지 않은 지표

2. Mean Absolute Error(MAE, 평균 절대 오차): 모델의 실제값 y와 예측된 y'의 차이에 대해 절대값을 취한 후 평균을 취해준다.

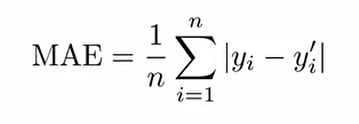
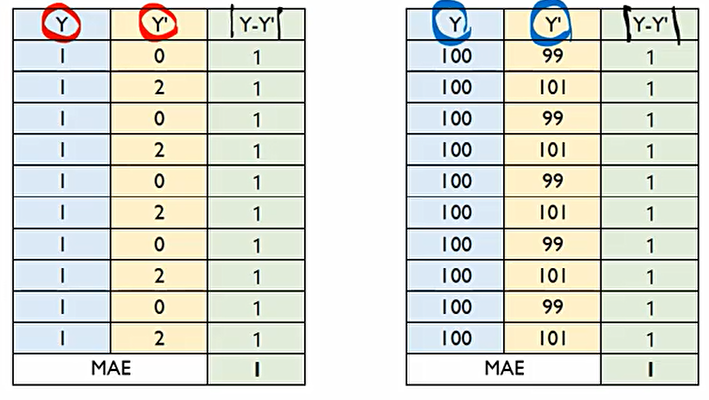
MAE는 다음과 같은 오류가 있다. 다음과 같이 둘다 MAE지표 상으로 1 값이 나왔지만 두 예측 모형이 똑같이 정확하고, 같은 성능을 가지는 것은 아니다.

그 이유는 MAE는 실제값 y와 예측된 y'의 절대적인 차이를 제공하지만, 상대적인 차이는 제공하지 못하기 때문이다. 원래 우리가 원래 맞춰야 하는 정답 y대비 몇 %나 틀렸는가, 오차가 났느냐를 표현해줄수 없다. 이에 MAPE를 사용한다.

3. Mean Absolute Percentage Error(MAPE, 평균 절대 비율 오차): 모델의 실제값 y와 예측된 y'의 차이에 실제값 y를 나눠 준 후, 절대값을 취하여 평균을 취해준다. 아래 식에 100을 곱하줘서 %로 표현하기도 한다.

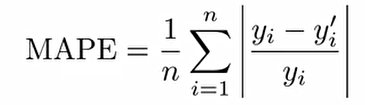
내가 맞춰야 되는 정답 대비 오차가 몇 %나 났는지를 보여주는 것.

4. Mean Squre Error(MSE, 평균 제곱 오차): 모델의 실제값 y와 예측된 y'의 차이에 대해 제곱을 취한 후 평균을 구해준다.

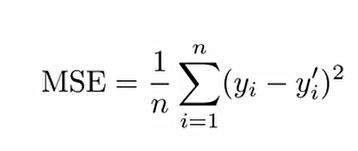
MAE, MAPE는 실무적인 관점에서 직관적인 이해가 용이하지만, 절대값을 사용하기에 모든 점에서 미분 가능하지 않다. 이를 analytically tractable하다고 한다. 미분 가능하지 않은 부분이 있어, 추가적인 분석이 어렵다는 것을 의미.

5. Root Mean Squre Error(RMSE, 루트 평균 제곱 오차): MSE에 루트를 씌워준다.

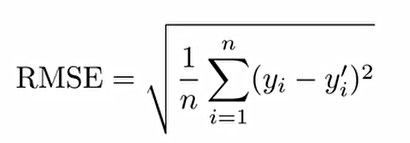
MSE를 사용하면 실제값 y와 예측된 y'의 차이의 제곱이 너무 커질 수 있으므로, 루트를 씌워줘서 크기를 조금 더 작게 한다.

데이터가 정규분포를 따르거나, 극단적인 Outlier가 없다면 RMSE는 MAE와 비슷해진다.

3. R Exercise

install.packages("moments")
library(moments)

왜도는 0, 첨도는 3정도가 되어야 정규분포가 된다라고 표현을 한다. 잔차의 정규성을 검정하기 위한 함수가 제공된 라이브러리인 moments를 다운로드 및 실행해준다.

# Performance evaluation function for regression
perf_eval_reg <- function(tgt_y, pre_y){
  
  # RMSE
  rmse <- sqrt(mean((tgt_y - pre_y)^2))
  # MAE
  mae <- mean(abs(tgt_y - pre_y))
  # MAPE
  mape <- 100*mean(abs((tgt_y - pre_y)/tgt_y))
  
  return(c(rmse, mae, mape))
}

실제값 y와 예측된 y'에 대한 평가지표들 정의. 이때 target_y와 prediction_y를 인자로 받는다.

# Initialize a performance summary
perf_mat <- matrix(0, nrow = 2, ncol = 3)
rownames(perf_mat) <- c("Toyota Corolla", "Boston Housing")
colnames(perf_mat) <- c("RMSE", "MAE", "MAPE")
perf_mat

이후 평가지표들을 계산한 후 각 항목에 대해 각 평가지표들을 보기 쉽게 테이블로 저장할 예정.

# Dataset 1: Toyota Corolla
corolla <- read.csv("ToyotaCorolla.csv")

# Indices for the activated input variables
nCar <- nrow(corolla)
nVar <- ncol(corolla)

id_idx <- c(1,2)
category_idx <- 8

csv파일 불러오기. nrow, ncol은 행의 개수, 열의 개수를 반환해주는 것이고, id_idx는 쓸데없는 차 이름, id 등 지우기 위하여 c 함수를 통해 [1,2]의 벡터 만들어주는 것. category_idx는 이후 무슨 연료를 사용하는 지를 dummy 변수화 하기 위해 설정

ㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡㅡ