Multivariate Data Analysis 3. Logistic Regression, Pilsung Kang 강의를 참고하였습니다.

https://www.youtube.com/watch?v=PsVyx6erzrU&list=PLetSlH8YjIfWKLpMp-r6enJvnk6L93wz2&index=8

1. Logistic Regression: Formulation

Logistic Regression은 회귀 이름이지만, Classification 알고리즘.

어려 남녀의 사진이 있고, 이 사진 중에서 남자, 여자를 구별해야 한다면 이때 x = 사진, y = 남/녀로 둘 수 있다. 이러한 문제를 binary classification 문제라고 한다.

Multiple Linear Regression은 설명변수 X들로 종속변수 Y를 설명하는 Linear relationship을 찾는 것을 목적으로 하였고, 이 과정에서 종속변수와 설명변수들 사이에 결합을 하게 해주는 회귀계수를 찾는 것이 학습이였다.

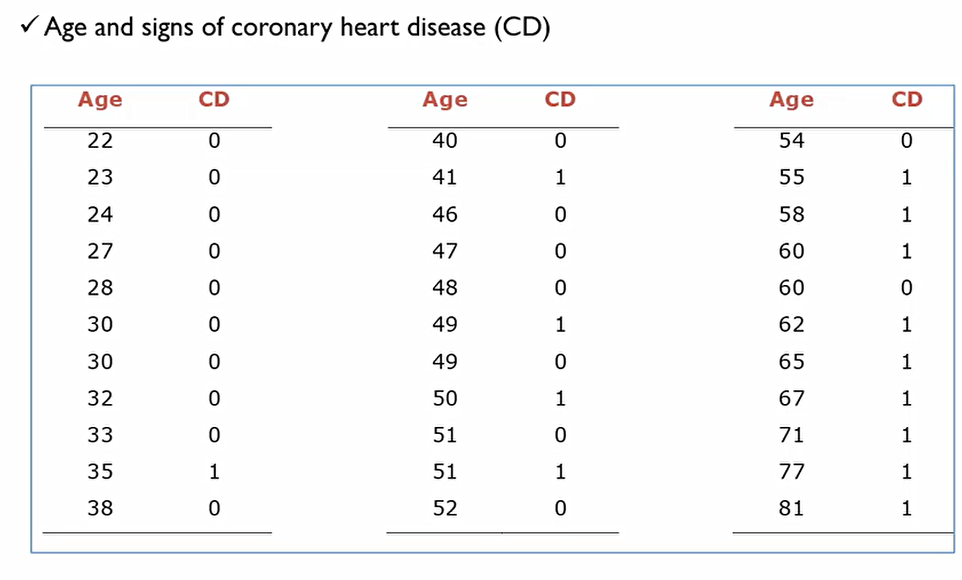
다음은 나이에 따른 심장병 유무의 데이터이다. 이를 그래프로 나타내면 다음과 같다.

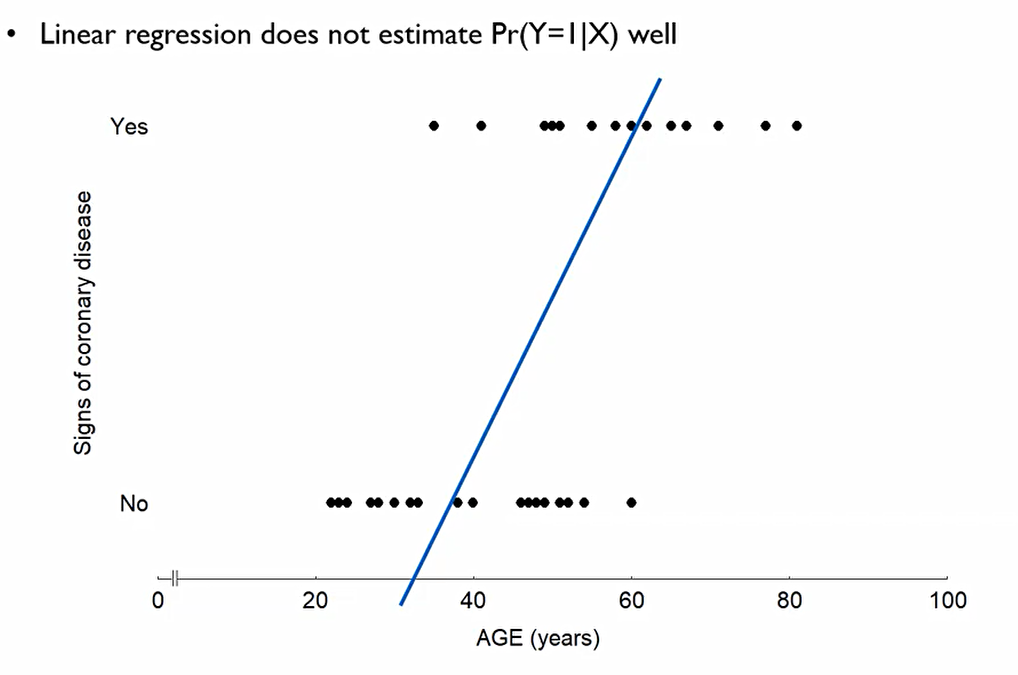
나이에 따라 없거나 있거나 둘중 하나가 되어버리기에, 선형회귀를 해봤자 제대로 이를 추정하고 있지 못함.

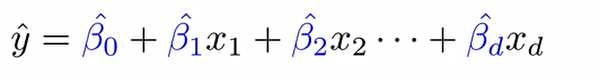
좌변 같은 경우에는 {0,1}로 값이 제한되지만 우변은 연속형의 숫자형이기에 값에 제한이 없다.

이를 변형하여, y = {0,1}을 추정하는 것이 아닌, P(y=1)을 추정해보자.

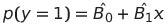
이렇게 한다면 P(y=1)은 [0,1]의 범위를 가지는 연속형의 숫자형이 된다. 그러나 여전히 우변은 [-∞,∞]의 범위를 가져 맞지 않는다.

또한 추정된 회귀값이 1 이상으로 올라가거나 0이하로 내려가버릴 수도 있다. 결론적으로 의미가 없어버림.

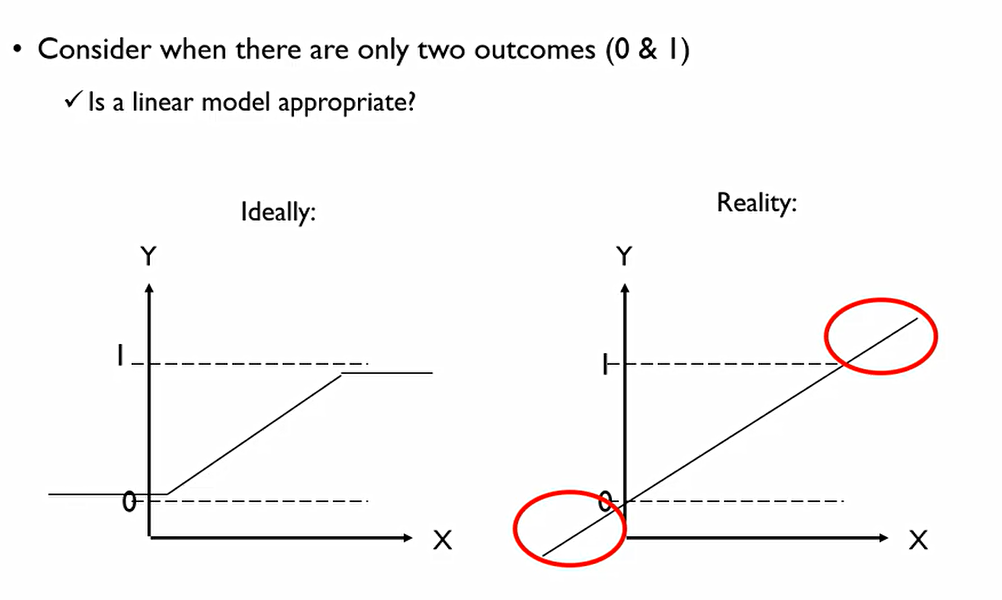
우리가 확률값을 추정하고자 하면 왼쪽과 같은 형태의 회귀식이 필요하나, 실질적으로 회귀식은 오른쪽 처럼 나오게 된다.

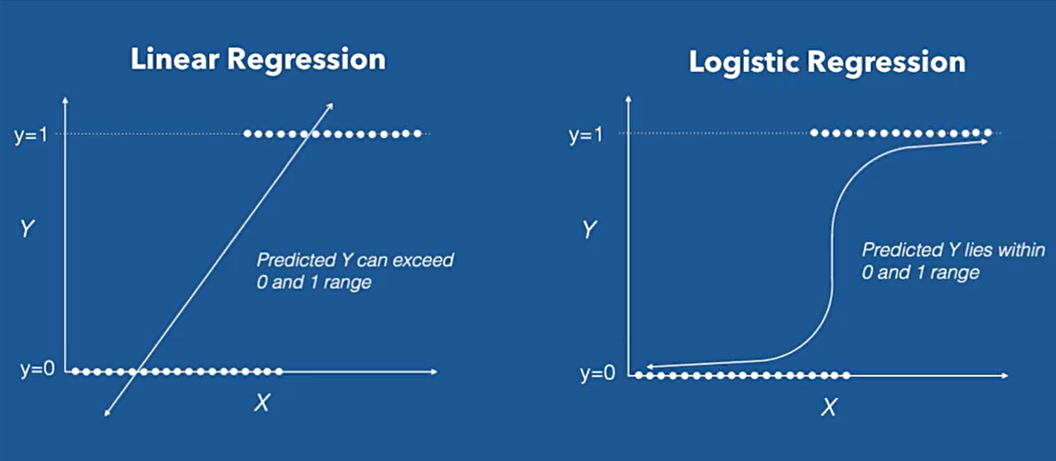
이에 이러한 경우, Logistic Regression을 사용하여야 한다.

• Binaray classification task에서 우리가 가질 수 있는 outcome는 0과 1 뿐이다.

• Regression equation은 범위에 대해 아무런 제약이 없다.

• 이에 X의 조합으로 가질 수 있는 범위와 Y가 가질수 있는 범위에 대해 mismatch가 발생한다.

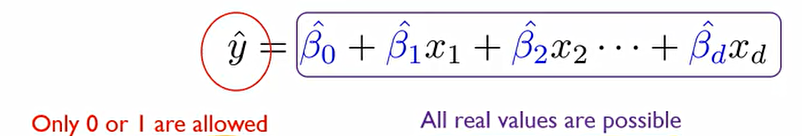
그러나, 오른쪽 회귀식을 유지함으로써 우리는 각각 회귀변수가 통계적으로 얼마나 유의미한지 판단할 수 있고(Ability to find significant variables), 해당 설명 변수가 증가하느냐 감소하느냐에 따라 성공확률 또는 특정 범주에 속할 확률이 증가하는지 감소하는지(explainability)를 알 수 있다.

Logistic regression의 목표는, 설명변수들을 가져다가 최종적인 outcome이 0/1이 되도록 하는 함수를 찾는 것.

Logistic regression 속성은 다음과 같다.

• Y를 linear regression처럼 취급하는 것이 아닌, y에 대한 logit함수를 output으로 사용하겠다.

• logit함수를 사용하면 설명변수들에 대한 linear function을 추정할 수 있다.

• logit은 이후 확률을 산출해 줄 수 있다는 장점이 있다.

logit 함수를 이해하기 위한 승산(odds)이라는 개념이 있다.

즉, 성공할 확률/성공하지 못할 확률이 승산이다.

왜 승산이라는 개념을 도입했을까?

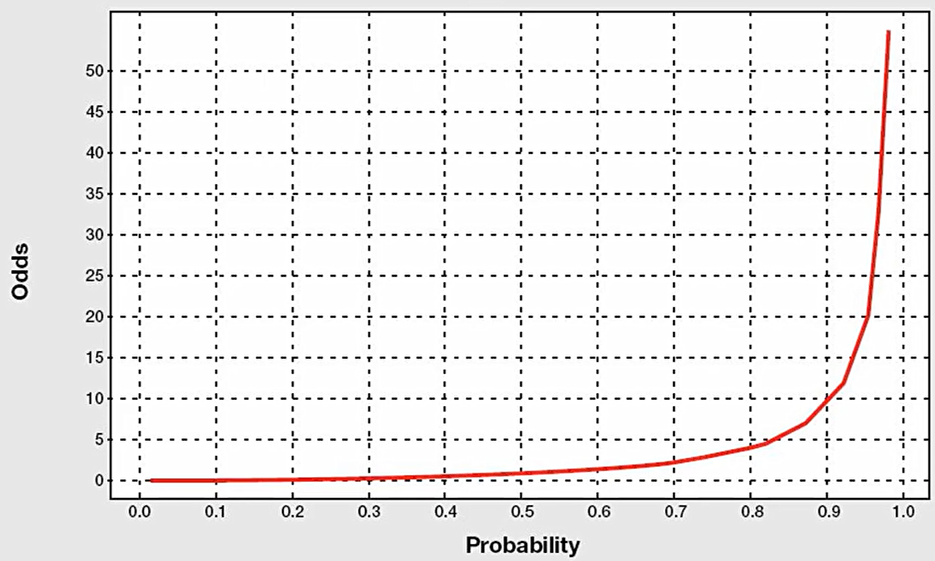
이때, P/(1-P)의 범위는 다음과 같기 때문이다.

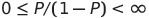
그렇다면 승산의 단점은 무엇일까?

• 0 < odds < ∞ : 음수를 가질 수 없다.
• Asymmetric

이러한 단점이 있기에 승산에 log를 씌운다.

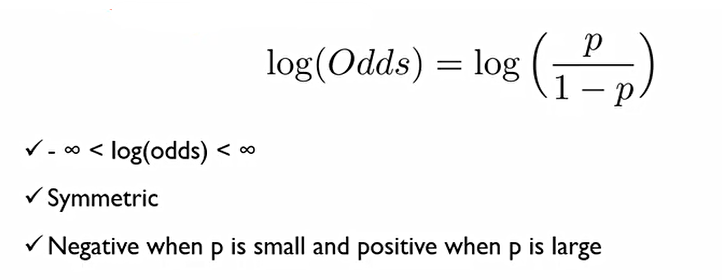
이에 결론적으로 다음과 같은 특성을 가지게 된다.

• -∞ < log(odds) < ∞
• symmetric

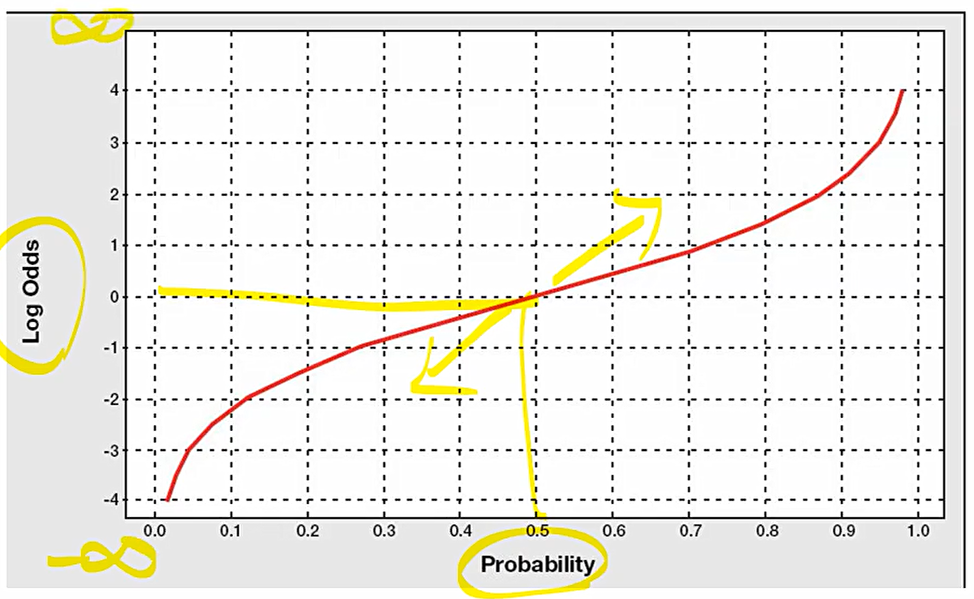
결국, 우리는 회귀분석을 위해 다음과 같은 함수를 사용하여야 한다. 성공확률에 대한 로그 승산을 선형식으로 추정하겠다는 것.

로그를 벗기기 위해 양쪽 항에 exponential을 씌워주고, 식을 정리하면 확률(p)도 구할 수 있다 !

2. Logistic Regression: Learning

Estimating the coefficeients

기존의 linear regression은 closed form으로, 데이터가 주어진다면 β^hat을 구할 수 있다.

그렇지만 Logistic regression은 그렇지 않다.

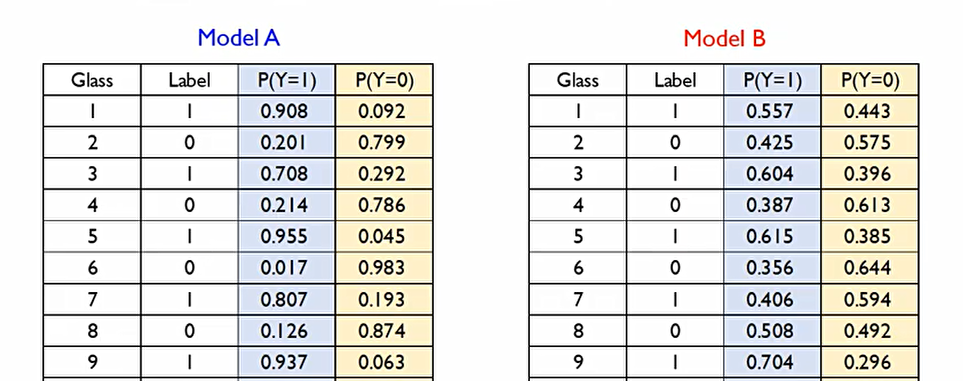
모델 A가 모델 B보다 정답 범주에 속할 확률을 항상 더 높게 산출하기에 모델 A가 더 좋은 모델이다.

likelihood function

각각의 객체들에 대해서 정답 class로 분류될 확률.

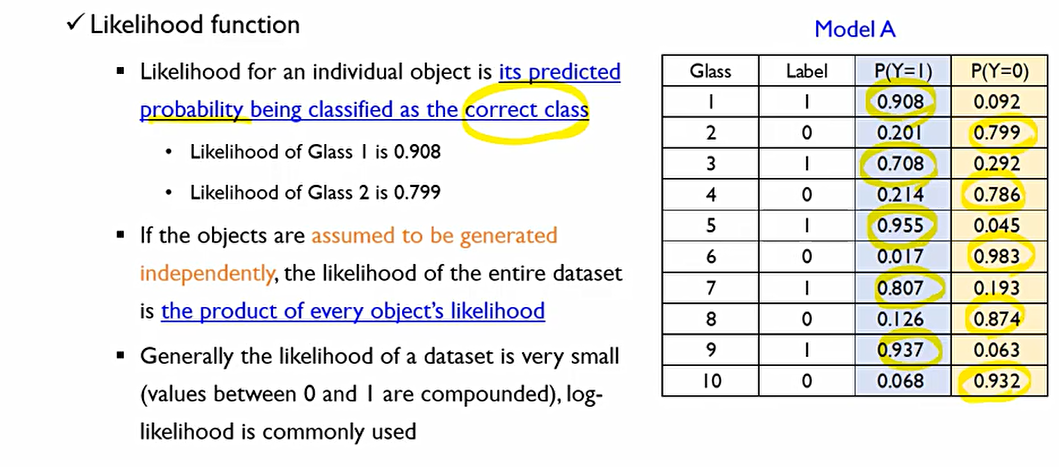
여기서, 각 라벨에 맞게 나온 확률이 각각 개체에 대한 likelihood 값. 여기서 모든 객체들이 i.i.d(independent identically distributed)되었다고 표현하는데, 두 사건이 독립적이라면 P(A,B) = P(A)P(B)값 해줘야하므로, 데이터셋에서 모든 데이터들이 독립적으로 수집되었다고 할 때 각 데이터의 모든 likelihood값 곱해주어야 한다.

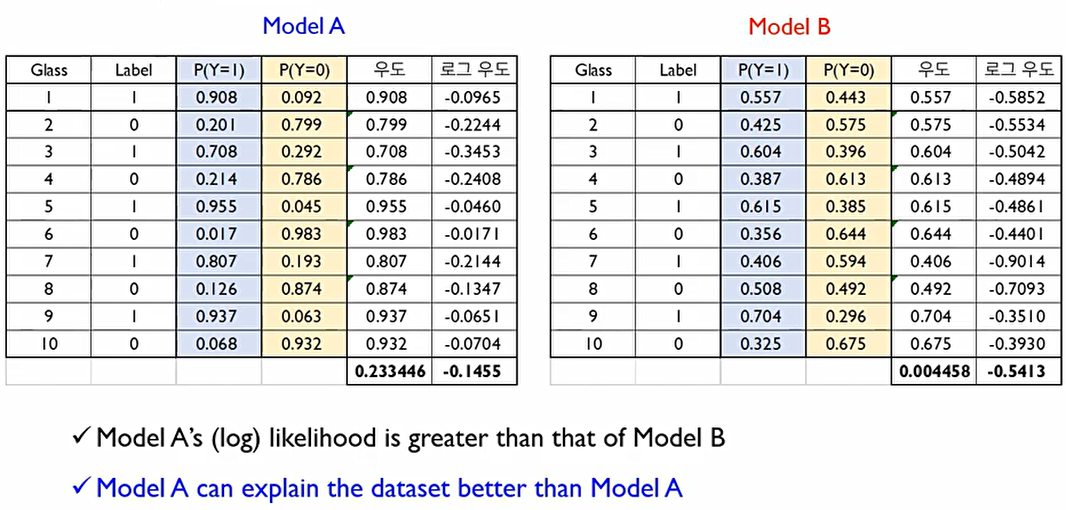
이렇게 데이터에 대한 우도를 구하기 위해서는 각 개체에서 구한 우도를 다 곱해주어야 한다.

그러나, 우도값은 기본적으로 0에서 1사이의 값이기에 개체가 많아질수록 0에 가까워진다. 이에 이를 해결하기 위해 로그우도 값을 사용한다.

이때 로그우도의 관점에서는 클수록 데이터를 잘 설명하는 것이므로 우도를 크게한다는 것은 로그우도를 크게하는 것이며, 로그우도를 크게만든다는 것은 음의 로그우도를 작게만든다는 것이다.

Max likelihood = Max log(L) = Min -log(L)

이를 하기 위한 방법론으로, Maximum likelihood estimation(MLE, 최대우도 추정법)를 사용한다. 결국 우리는 데이터셋이 가지는 likelihood를 최대화하는 coefficients를 찾고자 한다.

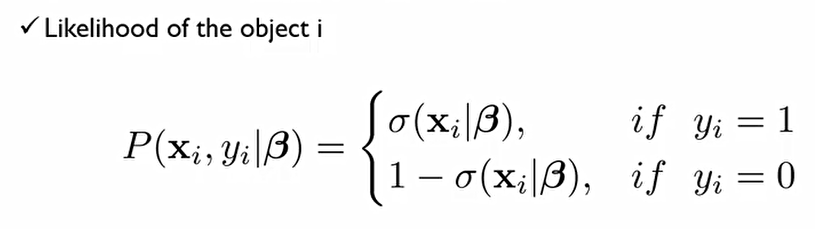
σ는 p(y=1)일 확률. β라는 어떠한 회귀계수가 추정되었다 치고, i번째 설명변수와 종속변수를 가지고 likelihood를 계산해보면 정답이 1에 속할 확률이면 위처럼 되어야 하고, 0에 속할 확률이면 아래처럼 되어야 한다.

이에, 위의 식을 한줄로 작성 가능하다.

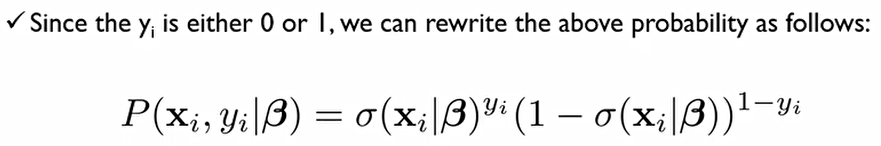
지금까지는 데이터 셋 각각의 경우의 likelihood를 계산한 것. 이를 바탕으로 전체 데이터 셋에 대한 likelihood계산해보자.

총 N개의 관측치 중에서, 각각의 likelihood 계산한 후 이를 각각 곱해주면 된다.

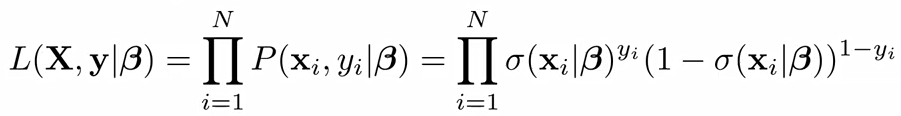
이때, 여기에 log를 씌운다면 product는 sumation으로 바뀌어서 나와 다음과 같은 결과가 나온다.

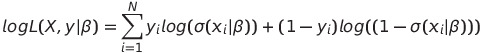
이때, 중요한 것은 이 표현식은 β에 대해 non-linear 식이고, 이에 explicit solution이 존재하지 않는다. 이에 적절한 최적화 알고리즘(ex. Gradient Descent) 등 사용하여 trial error 통하여 최종적인 해를 찾아가는 것.

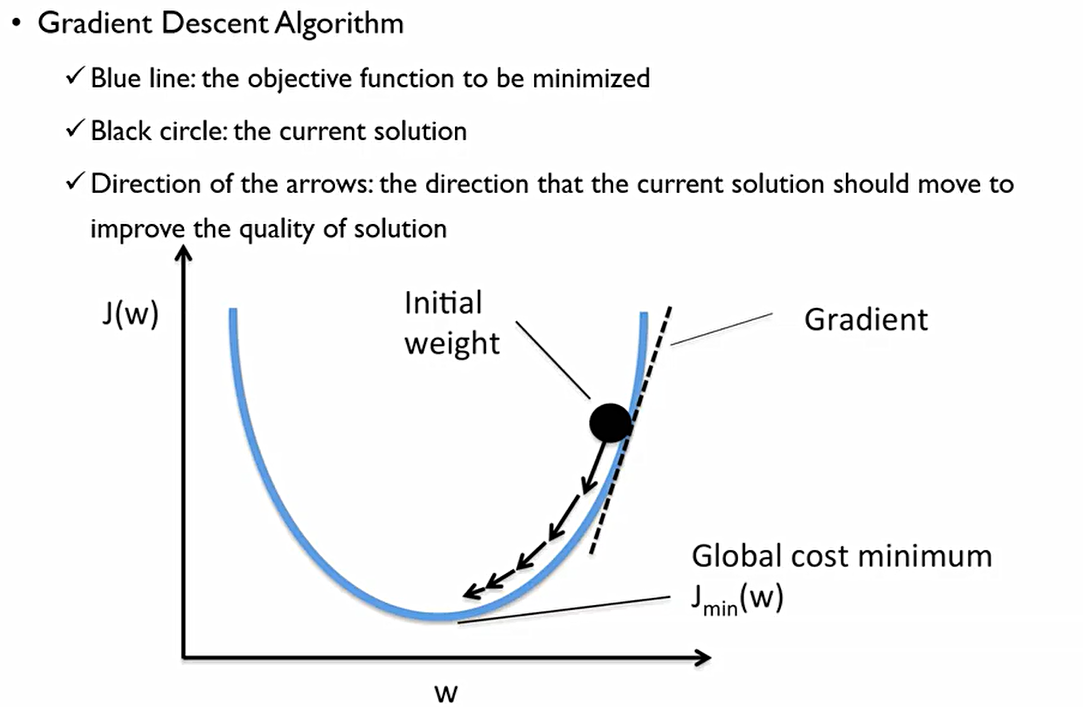
우리는 β를 구하기 위해 Gradient Descent방법을 사용한다.

• 최초에 β는 무엇인지 모르기에 랜덤한 숫자를 무작위로 지정해준다. 이를 initial weight라고 한다.

• 우리가 추정해야 하는, 최소화 해야 하는 함수를 파란색 선이라고 가정한다. 이를 Minimize해야 한다.

• 이때 J(W)는 비용함수로 여기서는 Negative log likelihood function의 함수가 되는 것. 이 함수는 일차 미분 가능하다!

우리는 일차도함수가 0인 β가 무엇인지는 모르지만, 어떤 β가 주어졌을때 β값을 기준으로 일차도함수를 구했을 때 도함수 값이 얼마냐에 대해서는 답을 할 수 있다.

여기서 Gradient는 접선의 기울기를 말한다. 이 Gradient의 부호에 따라 우리는 최적점을 찾아갈 수 있다. 이것이 0이 아닐 경우 우리는 최적점에 있지 않은 것이고, 최적점에 가려면 어디로 가야하느냐에 대한 방향에 대해 정보를 얻을 수 있다.

여기서 weight w는 우리가 찾고자하는 β^hat이며, cost function은 Log likelihood. 이때 다음과 같은 정보들을 우리는 알 수 있다.

• Gradient가 0인가?
  YES: 최적해이므로 학습을 끝낸다.
  NO: 현재가 최적해가 아니므로 더 향상시킬 방법이 있다. 더 학습하자

• 우리가 0이 아닌 Gradient를 가질 때, 어떻게 더 향상시키는가?
  Gradient에 대해서 정방향이 아니라 역방향으로 움직이자. Gradient가 양수이면 가중치 및 미지수는 감소시키고, 음수이면 가중치 및 미지수를 증가시킨다.

• 얼마나 움직여야 하나?
  잘 모르니까 알아서 조금씩 가라! 알아서 적당히 수렴할 것이다.

**Theoretical Background

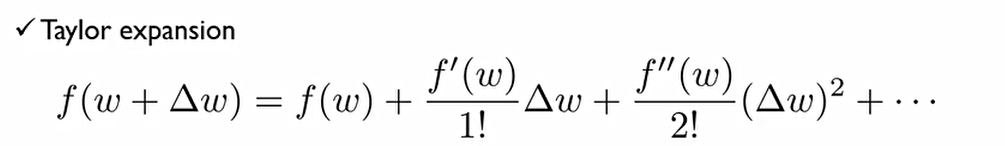
어떤 함수의 변동폭이 그렇게 크지 않을 때, 이렇게 무한급수로 표현될 수 있다. 이를 Taylor expansion이라고 한다.

Δw가 매우 작으면, 2차 식을 0으로 간주하여 식을 근사시킬 수 있다.

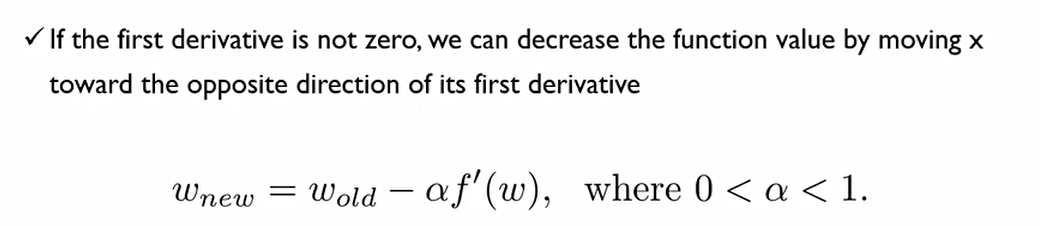
이에 새로운 β^hat을 구하기 위해서는 이전 β^hat을 f'에 해당하는 도함수의 반대방향으로 보내야 한다.

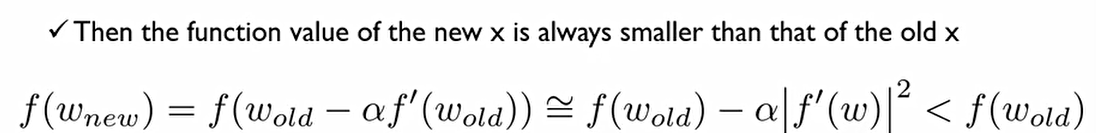
이 반대방향으로 정의해준 새로운 β^hat을 함수에 넣어주게 된다면 tylor expansion에 의해서 위처럼 나오게 된다. 즉, 다음과 같이 도함수의 반대방향으로 움직이게 된다면 항상 이전보다는 작아질 수 있다는 것을 보장해주게 된다.

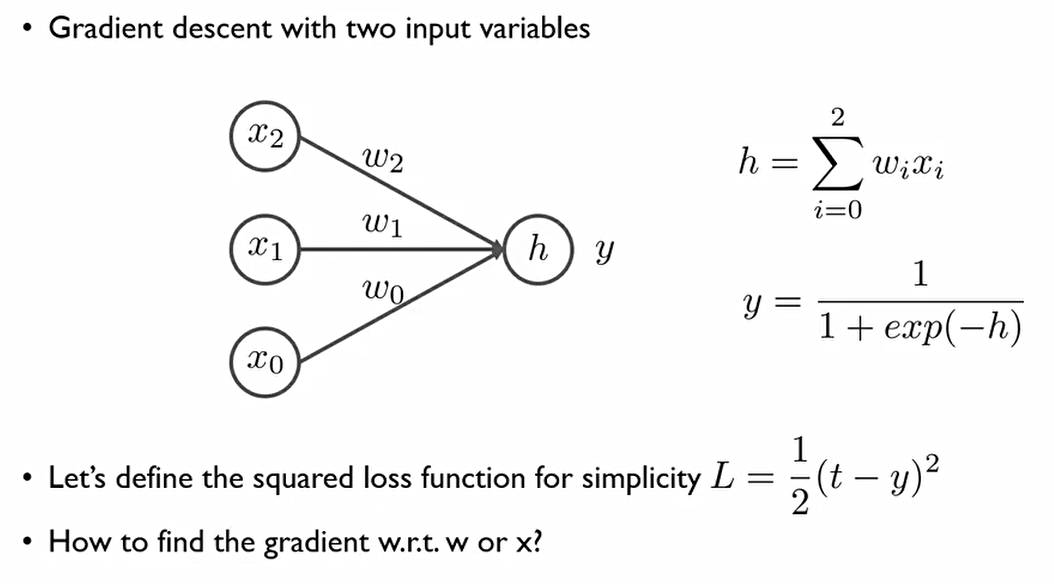
이후 배울 Neural network에 이를 대입해서 설명해보자.

x는 설명변수, w는 β, h는 다음과 같다.

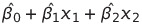
y는 logistic 회귀분석을 통해서 해당하는 값을 표현한 것.

여기서 loss 함수는 위와 같이 사용. 원래는 log likelihood를 사용해야 하나 여기서는 직관적인 설명을 위해 이를 사용한다. 이때 t값은 정답(1,0)이고, y는 로지스틱 회귀분석에 의해 나타난 P(y=1)일 확률이다. 즉, 각 레이블에 대한 차이가 0에 가까울수록 좋은 것이다.

우리가 필요한 것은 미지수는 w이기 때문에, 손실함수를 w에 대해 미분한 것이 필요하다.

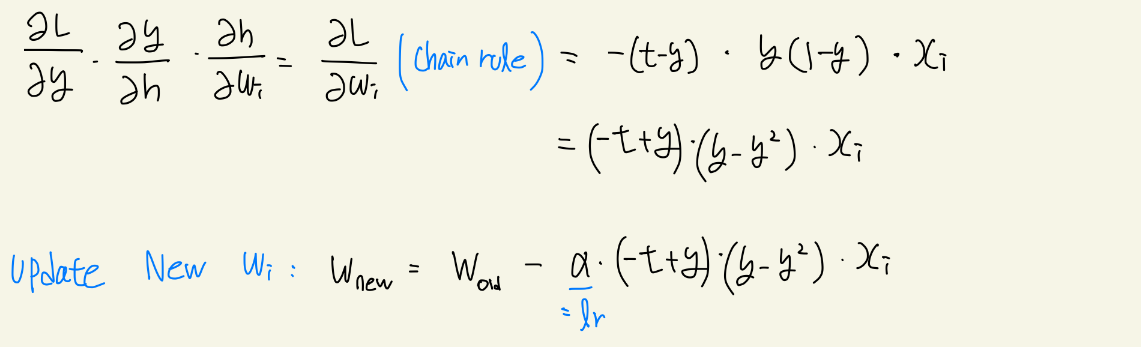
(y-t)는 y가 모형에 의해 추정된 값, t가 정답이였기에 둘 사이의 차이가 적으면 모형을 덜 움직이겠다는 것. 차이가 크면 많이 움직인다.

x_i 가중치를 업데이트함에 있어서 그 가중치와 연결되어있는 설명 변수의 값만 영향을 끼치겠다는 것. 예를 들어 β2를 업데이트 하는데는 β2만이 영향을 끼친다는 것.

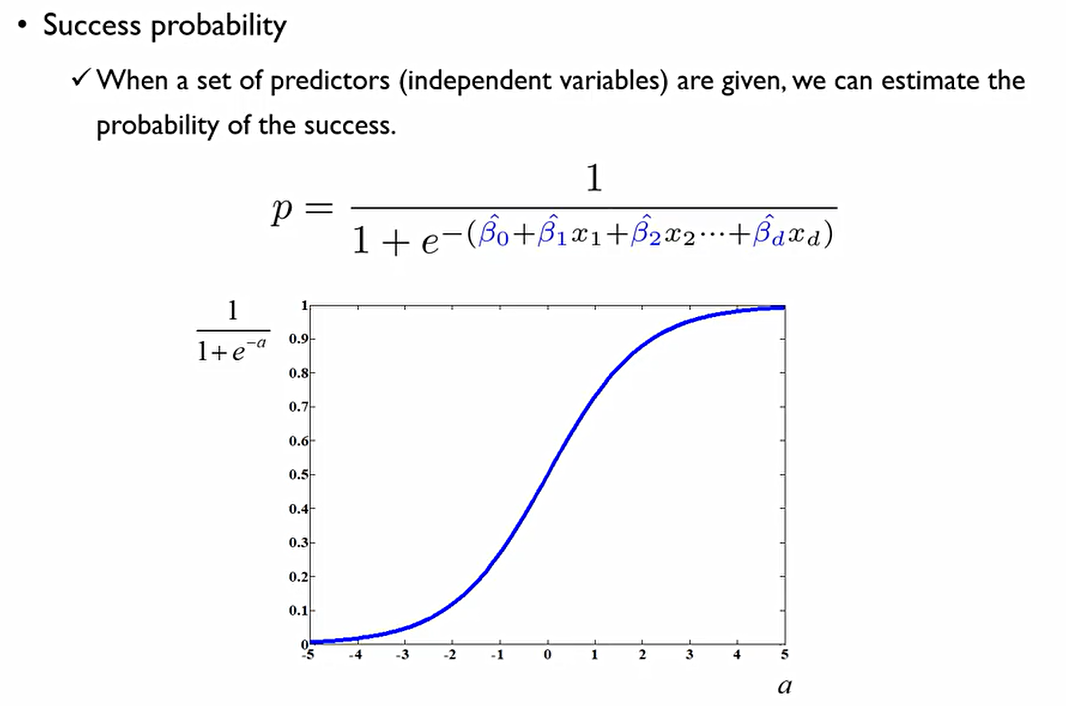
이렇게 업데이트가 되면서, 이제 우리는 binary classification 문제를 해결해야 한다. 이때, e의 위 첨자에 해당하는 부분을 a로 두고 그래프를 그리면 다음과 같은 그래프가 나온다.

이때 S자 형태의 curve가 나타나게 되는데, 이는 매우 중요한 의미를 가진다.

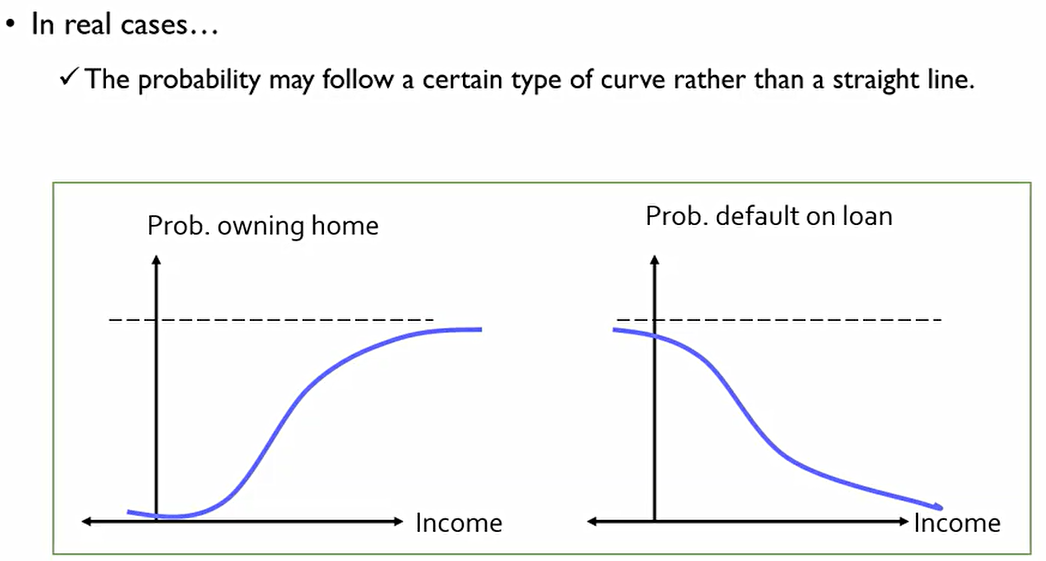
그 이유는 실생활에서는 어떤 변수가 또 다른 변수에 항상 선형적으로 비례하는 것이 아니라 특정 구간에서만 선형성을 가진다. 즉, 실생활에서는 보통 S자 curve를 그린다.

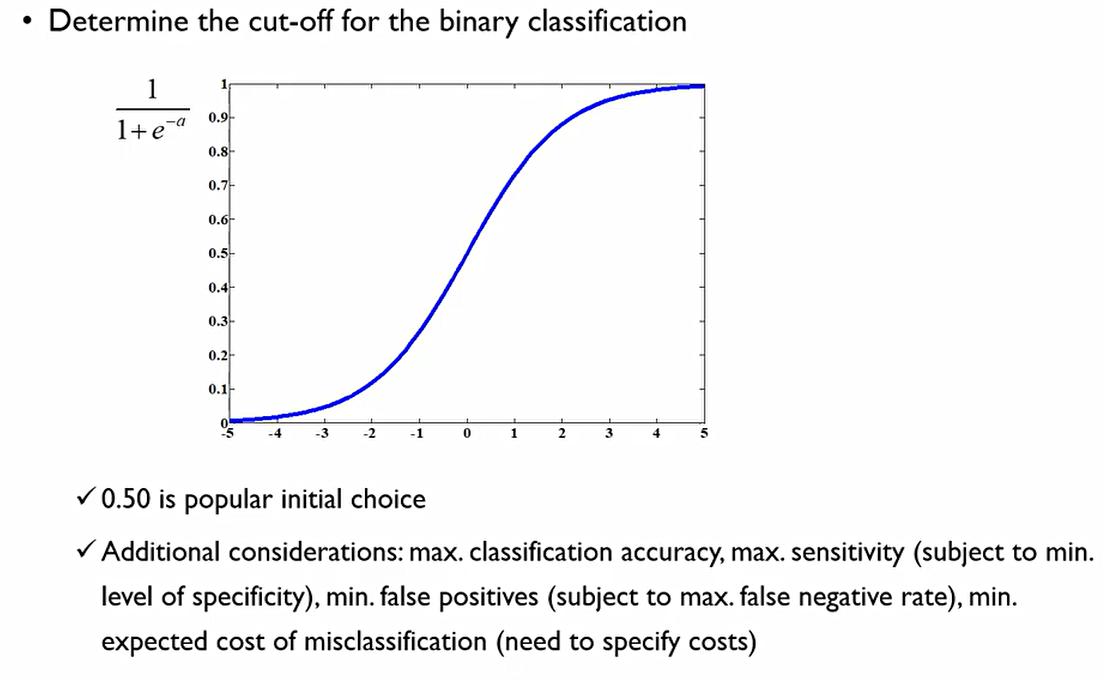
그래서 어떻게 Binary classification을 할 수 있을까? 우리는 확률값을 알지만, 이를 어떻게 0과 1 값으로 나타낼 수 있을까? 이를 바꾸는 과정을 cover 또는 Threshold라고 한다.

확률값을 0.5를 기준으로 이보다 높으면 1, 아니면 0인 것. 그러나 기준점(cut-off)은 각자 Task에 따라 맞춰 사용해야 한다. 사전 확률이 낮으면 이에 따라 cut-off값도 낮춰줘야 한다(제조업의 불량개체 확인). 반대일 경우는 높여주지만, 이러한 경우는 거의 없다.

3. Logistic Regression: Interpretation

회귀계수를 설명하는 방식

선형회귀분석은 종속변수가 설명변수들의 선형 결합으로 표현된다. 이에 설명변수의 실질적인 값을 표현하게 되고, β들의 값을 명확하게 표현할 수 있다.

그러나 Logistic regression은 로그 승산을 계산하므로, 회귀식을 구성하는 β값들에 대한 해석이 어려워진다. 성공확률로 표현하면 아래와 같은 회귀식이 만들어지기 때문이다.

이를 굳이 해석하면, 대응하는 설명변수가 1만큼 증가할때 성공확률이 로그 승산에 대응하는 β만큼 증가한다는 것. 하지만 Intuitive하지 않다.

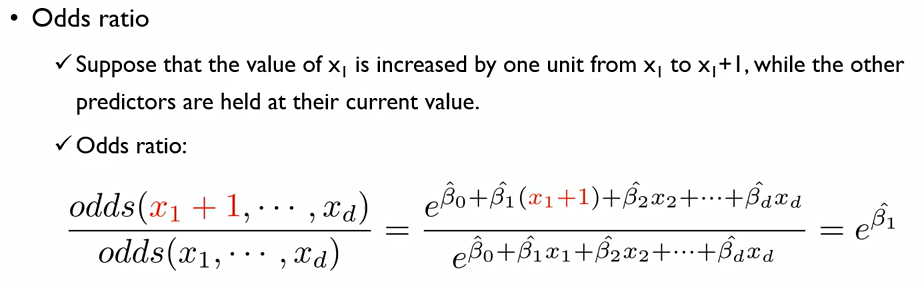
이에 Logistic regression에는 Odds ratio라는 개념이 존재한다.

이는 한 설명변수 x_1이 한 Unit만큼 증가했을 때(x_1 to x_1 + 1), 다음과 같아진다. 이때, 다른 설명변수들은 변화하지 않아야 함.

분모는 원래 x값들이 가지고 있던 값들을 의미하고, 분자는 x1이라는 변수만 하나 변화시켰을 때의 값. 즉, 성공확률/실패확률값을 의미한다.

특정한 설명변수가 1만큼 변화했을 때 다음같이 변화한다. 이때 이의 해석은 다음과 같다.

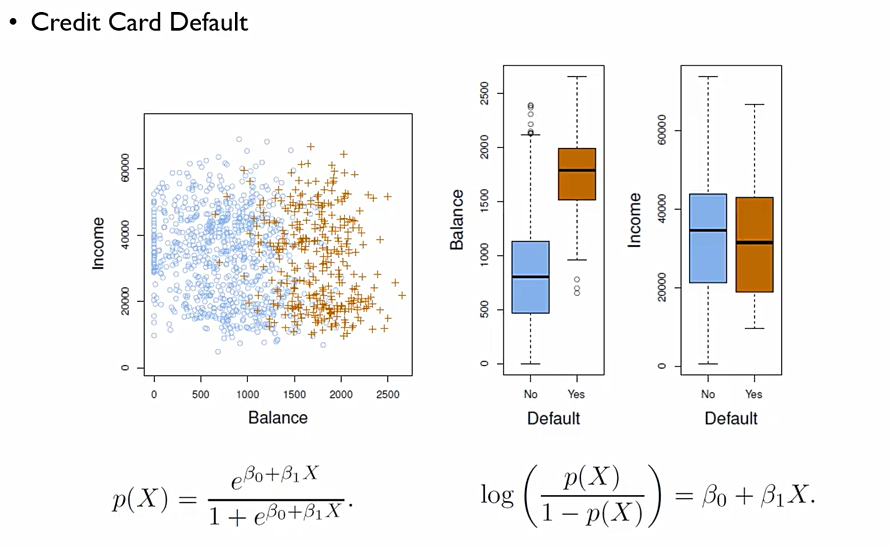
이를 보면, Income과 Balance라는 변수들이 있다. 이때, Balance는 통계적으로 유의미하지만, Income은 그다지 유의미하지 않다는 것을 알 수 있다.

Balance만을 가지고 표를 만들면 다음과 같은 값이 나온다. 이때 Balance의 p-value값을 보면 통계적으로 매우 유의미함을 알 수 있음.

이를 다음과 같이 계산할 수 있다. 확률로 따지면, 갚아야 할 돈이 1000달러인 사람이 default될 확률은 0.6%정도 되는 것.

2000달러로 증가하면, 58.6%로 급격히 상승한다.

Multiple variable을 가지고 회귀분석을 진행해보자.

p-value에 관해서는 α는 0.05라고 가정한다면 유요한 변수는 balance와 student.

coefficient에 관해서 balance가 증가하면 defalut확률이 늘어나고, 학생이면 감소한다.

유의미한 변수를 골라내는 데 사용. α를 0.05나 0.01로 설정하여 이보다 낮으면 유의미할 확률 높다고 가정.

input 변수가 1만큼 커졌을 때 성공에 대한 승산이 얼만큼 변화하느냐.

Odd ratio가 1보다 작을 때는 coefficient가 -값을 가지고, 아니면 +값을 가진다.

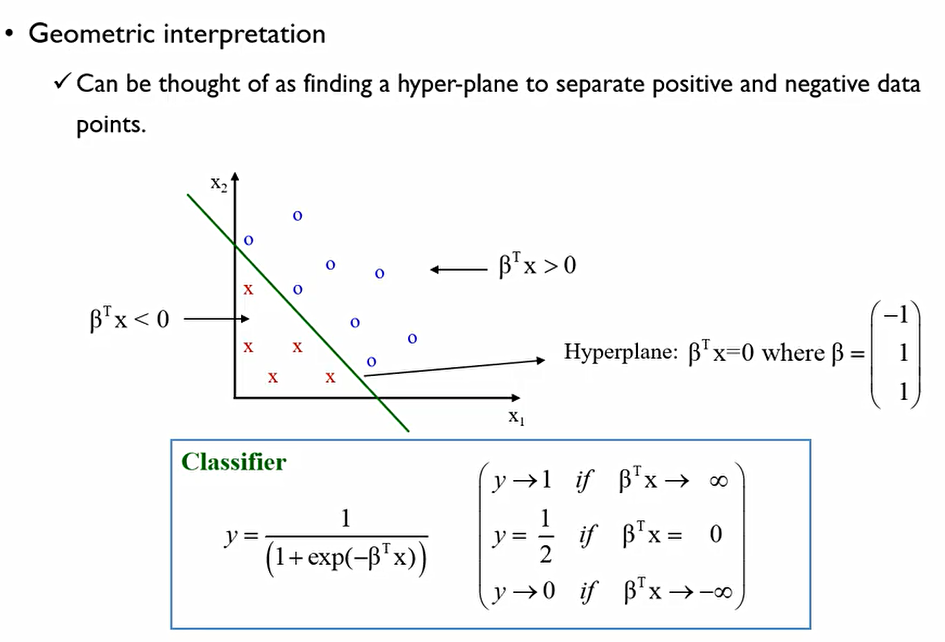
그렇다면 Logistic regression이 기하학적으로 무슨 의미를 가지는 것일까? 2개의 설명변수로 이루어진 범주가 있다. 이를 가장 잘 구별하는 직선을 찾는 것. 2차원일 경우는 직선, 3차원일 경우는 평면.. 등으로 넘어간다. 초평면을 찾는다고 표현한다.

이때, 직선이 의미하는 것이 P=0.5. 이를 기준으로 위로 간다면 P는 1에 가까워지는 것이고, 아래로 간다면 P는 0에 가까워진다고 말할 수 있다.

이 식은 odds에 관한 식이다.

이때, 회귀계수β가 증가한다면 성공확률은 증가하는 것이고, 회귀계수β가 감소한다면 성공확률이 감소하는 것. 이는 로지스틱이나 선형회귀분석이나 공유하는 성질.

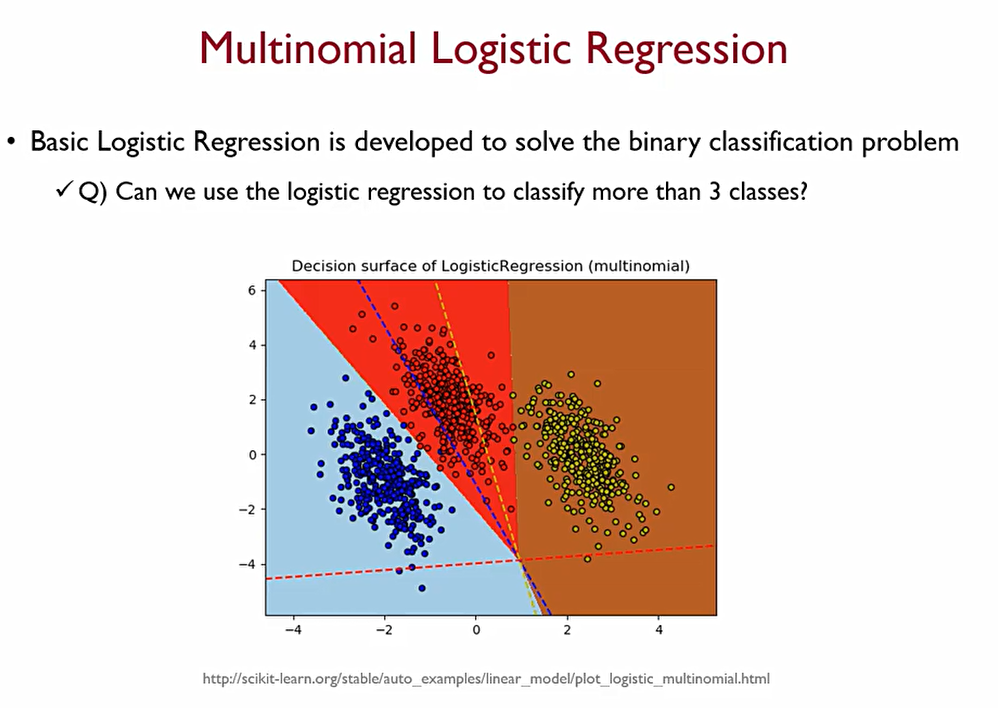
그렇다면, 다범주로도 로지스틱을 사용할 수 있을까?

Multinomial Logistic regression을 사용한다면 이것이 가능하다.

핵심은 odds를 계산할 때, P/(1-P)를 success/fail로 표현할 수 있다. 그렇다면 Multinomial Logistic regression에서는 baseline class를 설정하여 이를 분모로 하는 odds를 여러개 만든다.

이렇게 만들면 K개의 Class가 있을 때, (K-1)개의 모델만 만들 수 있다.

이때, 모든 Class들의 성공확률값을 더하면 1이 되어야 하는데, 이를 이용하여 나머지 한 개의 모델을 만들 수 있다.

4. Classification Performance Evaluation

전반적인 분류모델에 대하여 어떻게 성능 평가를 할 수 있을까?

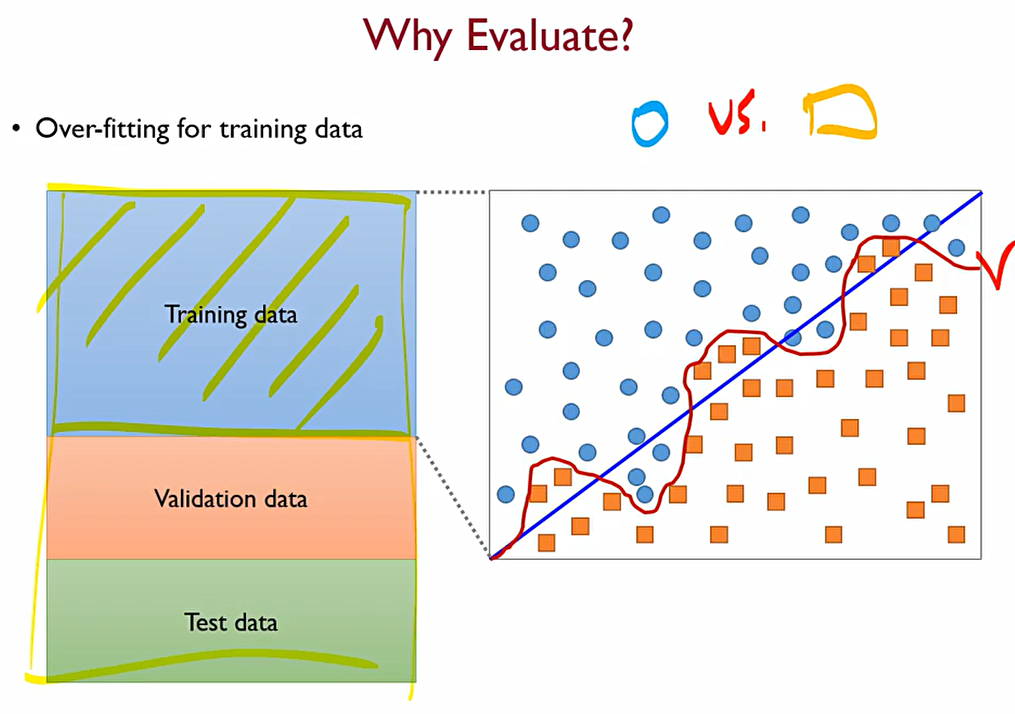
학습용 데이터만 보았을 때, 파란색 선보다는 빨간색 선이 조금 더 좋게 학습이 되었다고 생각할 수 있다. 그렇지만, Real data가 가지는 특성을 생각해봐야 한다. 우리가 Real data를 바탕으로 모델을 식으로 만들었을 때, y=f(x)+ε 로 나타낼 수 있는데, 이는 ε 즉 우리가 어떻게 할 수 없는 변동성 에러를 가지고 있다는 것.

즉, 빨간색 처럼 학습을 하게 된다면 학습용 데이터가 가지는 변동성까지 학습해버렸다는 것

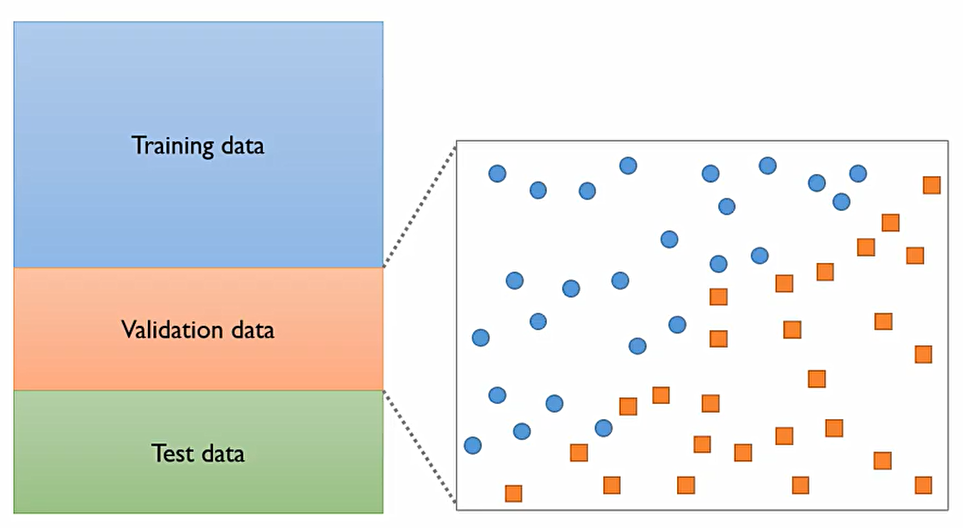
이후 Validation data로 검증을 해본다면, 파란색 선이 validation data에 대해서는 더 좋게 결과가 나온다는 것을 알 수 있다.

즉, 우리는 학습용 데이터를 잘 맞추는 모델이 아닌, 새로운 Real world의 데이터가 들어왔을 때 이를 잘 설명할 수 있는 모델을 원한다.

Classfication과 Prediction(Regression)에는 다양한 모델이 존재하는데, 어떤 모델이 제일 좋을 것이며, 어떤 모델에 어떤 hyper parameter를 써야 최고의 성능을 낼 수 있을까?

이때 학습데이터가 아닌 테스트데이터에 따라 최고의 조합을 찾아야 한다.

이에 best model을 선택하기 위해서는

• 하이퍼 파라미터가 존재하는 알고리즘 별로 best hyperparameter의 조합을 찾아야 한다. 이를 validation에서 찾는다.

• 이후, 찾은 best model의 조합 중 가장 좋은 모델을 찾기 위하여 Test데이터에서 이를 찾게 된다.

우리는 2범주 분류를 기준으로 보았을 때 혼동 행렬(Confusion Matrix)/정오행렬를 만들 수 있다. 이때, 행은 정답, 열은 예측된 값을 의미한다 여기서 성능이 높은 모델은 대각행렬의 값이 높고, 아닌 부분들의 값은 낮아야 한다.

Binary classification에서는 관례적으로 내가 관심을 두는 범주를 옮고 그름을 떠나 positive(1)로 설정한다.

이때, Misclassification error는 보통 대각행렬이 아닌 부분/전체 값으로 구할 수 있고, Accuracy는 대각행렬 값/전체 값으로 구할 수 있다.

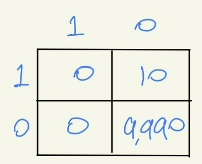
이때 Balanced correction rate(BCR)이라는 값이 존재한다. 다음의 예시에서 ACC는 0.999의 값이 나오지만, 실질적으로는 불량을 단 한건도 판단하지 못한 의미없는 모델이다.

이에 Balanced correction rate(BCR)은 각각의 범주들에 대한 정확도를 따로 계산한 후 기하평균을 씌운다.

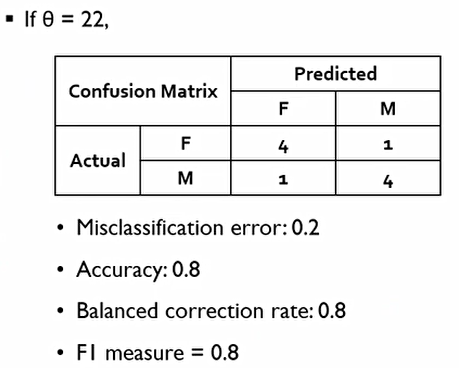
F1-Measure는 이와같이 사용된다. 우리는 F를 제대로 측정하는 게 중요하면서, 1종 오류, 2종 오류에 해당하는 부분(대각행렬이 아닌 부분)을 낮추는 것이 매우 중요하다. 이때, Recall, Precision은 다음과 같다.

결국, F-1 Measure는 Recall과 Precision의 기하평균으로 계산할 수 있다.

지금까지 설명한 Measure들은 모두 confusion matrix때문에 cut-off라고 하는 분류 기준점에 영향을 받는다. 즉, Measure들은 cut-off에 종속적이다.

일반적인 알고리즘은 각각의 범주에 해당하는 likelihood나, 확률, degree of evidence를 내어주게 된다.

classification performance는 cuf-off에 매우 크게 의존된다. 이에, cut-off에 독립전인 Performance measure가 필요하다. 이를 Receiver operating characteristic(ROC) curve라고 한다.

이 ROC curve를 설명하기 위해 우리는 Area Under Receiver Operating Characteristic Curve(AUROC)를 사용할 것. 다음의 데이터를 확인해보자.

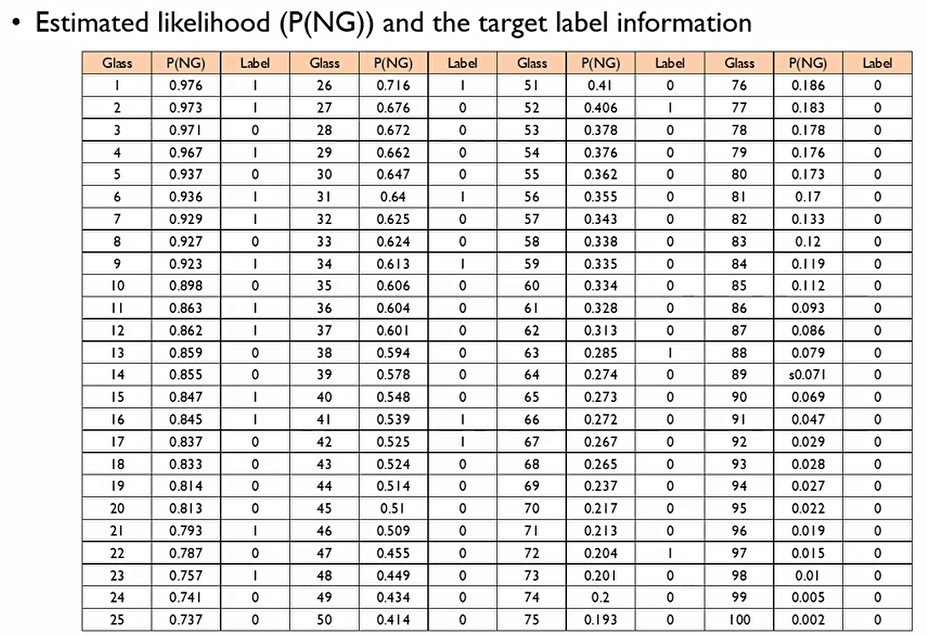
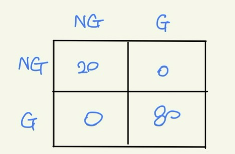
좋은 모델이라면, likelihood를 기준으로 나열한다면 첫번째부터 스무번째까지 모두 Label이 1이어야 최고의 결과물이 나온다. 이에 cut-off를 스무번째 P(NG)로 설정하면 다음과 같은 Confusion matrix가 나올 것이다.

이때, performance가 cut-off에 따라 바뀐다면, 본질적인 performance를 측정할 수 있는 방법은 없을까?

본질적인 performance에 대해서 어떻게 측정할 것인지 그리는 것이 ROC curve.

• 각각의 모든 Record를 우리가 원하는 범주에 대한 확률값(P(NG))에 대해 내림차순한다.

• 각각의 Case(조합)에 대해서 True positive rate와 false positive rate 각각에 대해서 다 계산을 해본다.

• 이렇게 된다면, 가능한 cut-off의 갯수는 몇 가지일까? 총 101가지가 될 것이다.

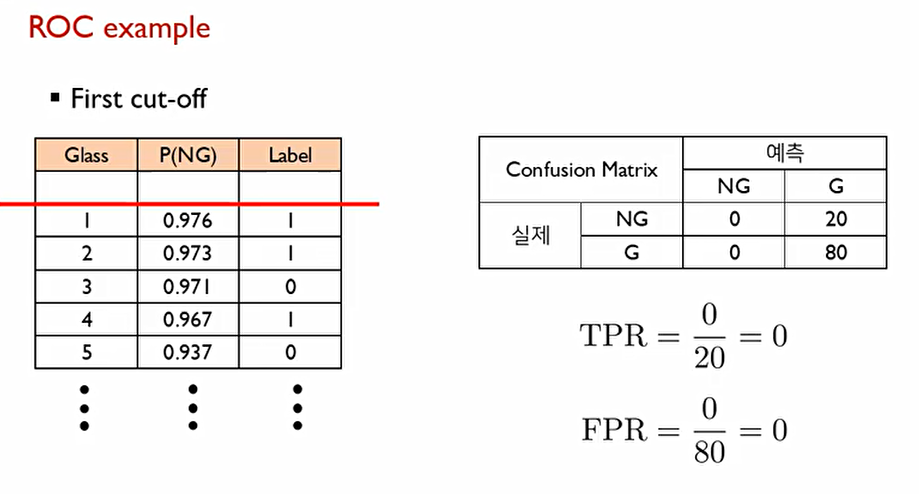
이때 True positive rate(TPR)은 0, False Positive Rate는 0이라는 값이 나온다.

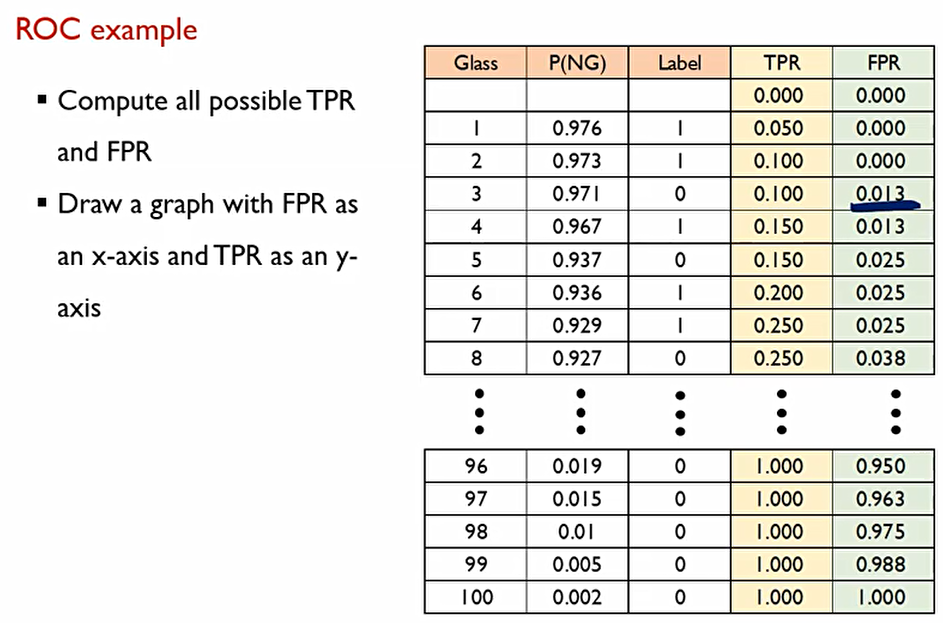
이렇게 처음부터 cut-off를 계산하여 마지막까지 계산하면 TPR과 FPR의 101개의 조합이 나온다.

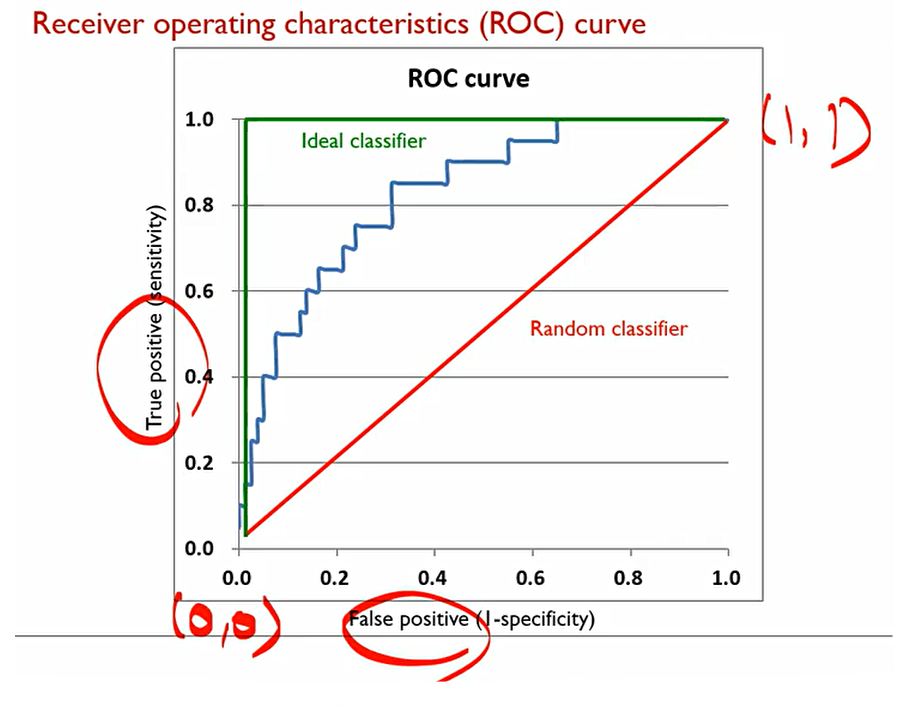
이때 이상적인 Ideal classificer는 다음과 같다. 이 경우에는 cut-off가 20일 때.

우리는 이때 컴퓨터에게 이를 얼마나 정확한지 하나의 숫자로 알려주어야 한다. 이를 Area Under Receiver Operating Characteristic Curve(AUROC)라고 한다.

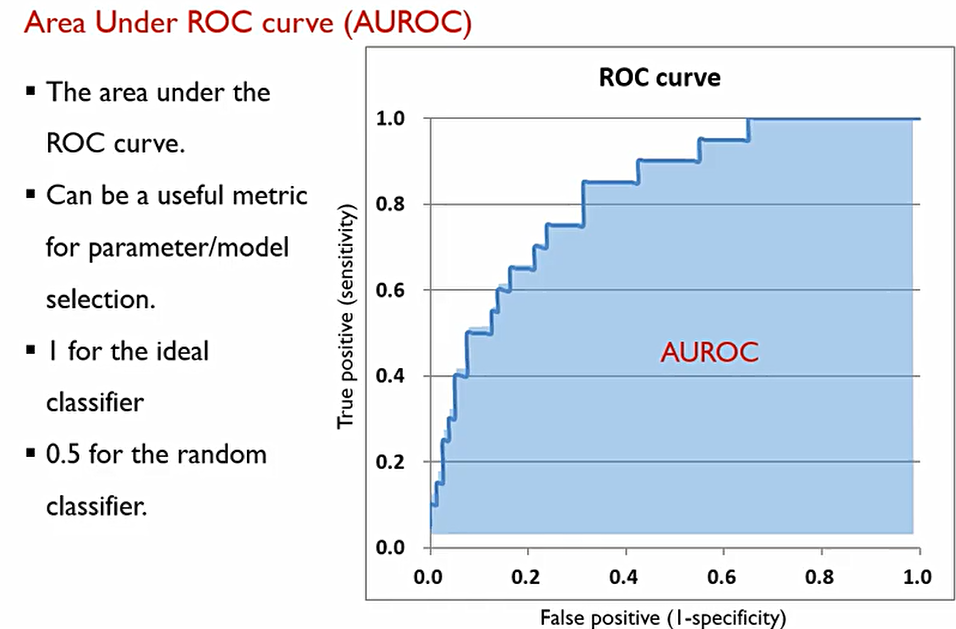
Area Under Receiver Operating Characteristic Curve(AUROC)는 이때 우리가 측정한 TPR과 FPR로 이루어지는 밑변의 넓이를 말한다. Ideal case일때 넓이가 1 이고, random classifier 경우에는 0.5이기에,
Area Under Receiver Operating Characteristic Curve(AUROC)값은 보통 다음과 같은 범위를 가진다.

0.5 ≤ AUROC ≤1

5. R Exercise