Multivariate Data Analysis 5. Decision Tree, Pilsung Kang 강의를 참고하였습니다.

https://www.youtube.com/watch?v=w6eCV1GzsLs&list=PLetSlH8YjIfWKLpMp-r6enJvnk6L93wz2&index=17

지금까지 우리가 배웠던 방법론들은 다음과 같은데, 이때 MLR은 Regression을 위한 방법론이고, Logistic Regression은 classification을 위한 방법론이였다. 이번에 배우는 Decision Tree는 이 Regression과 classification을 둘 다 할 수 있는 방법론.

1. Classification Tree

공짜 점심은 없다.: 어떠한 단일 분류기도 다른 분류기들에 비하여 더 낫다라고 말할 수는 없다.

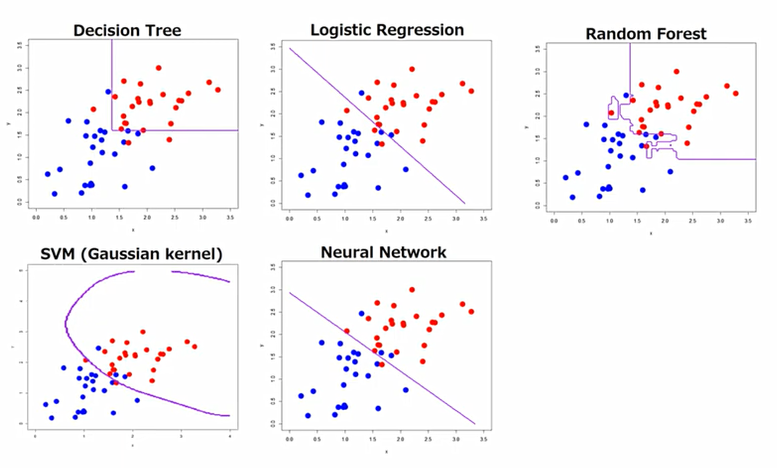
Logistic은 주어진 데이터가 있을 때, 이 데이터들을 잘 구분하는 하나의 직선을 구하는 것.

Classification Tree

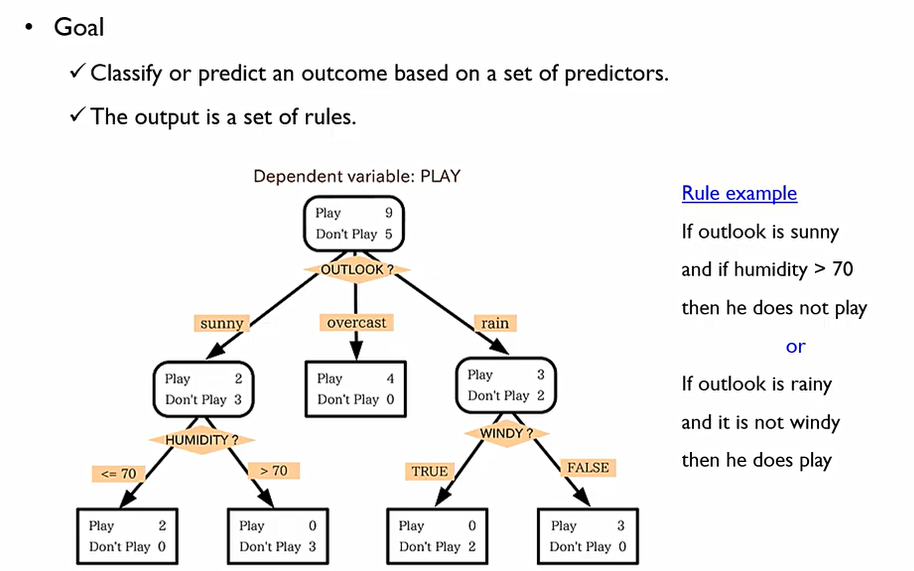
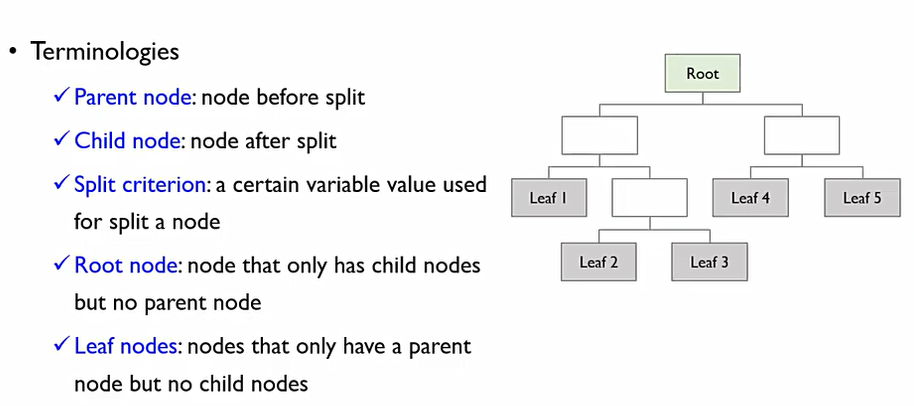
변수들의 조합들을 이용하여 분류하고자 하는 규칙을 만드는 것. Output이 규칙들의 집합(TREE)으로 나오게 된다. 각각의 항목들을 Node라고 부르며, 맨 위의 노드를 Root Node라고 한다. 맨 아래 노드는 Leaf Node. 화살표가 시작되는 것은 Parent Node, 이 화살표들을 통하여 갈라지는 노드들을 child Node.

Split criterion은 어떤 기준으로 부모 노드에서 자식노드로 구분되는 것인가에 관한 기준. 우리는 이 구분 기준들에 대해서 학습을 하게 되는 것.

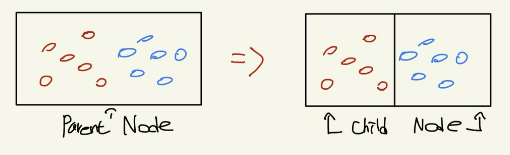
이때, Tree의 가장 큰 특징은 예측 결과물에 대한 설명을 해줄 수 있으며, 사람의 언어로 이해할 수 있도록 설명해줄 수 있다.는 것

이후에 배우는 모델들 같은 경우에는 왜? 라는 질문에 사람의 언어로 대답하지 못한다. 그렇지만 수학적인 Formulation은 갖추고 있다.

CART(Classification And Regression Tree)는 이해하기 쉽고, 정규화나 결측치가 있어도 잘 돌아가며(현실적이고 유용성이 높다), Numerical하고 Categorical한 데이터가 있어도 한번에 handling할 수 있다.

이때, 두 가지의 핵심적인 아이디어가 존재한다.

• Recursive Partitioning(재귀적 분기)

부모노드로부터 자식노드를 찾아가는 과정. 어떻게 하면 더 잘 분기할 수 있을까.

데이터를 구분하는데, 한번만 하는 것이 아닌 child node에서도 특정한 조건을 만족시킬때 까지 여러번 더 분기하는 것. 이때, 아무렇게나 분기하는 것이 아닌 분할 후 purity가 더 증가하는 방향으로 분할한다.

CART에서 사용하는 것은 Gini Index. 이는 A라는 영역에 m개의 class가 있을 때 다음과 같이 계산할 수 있다.

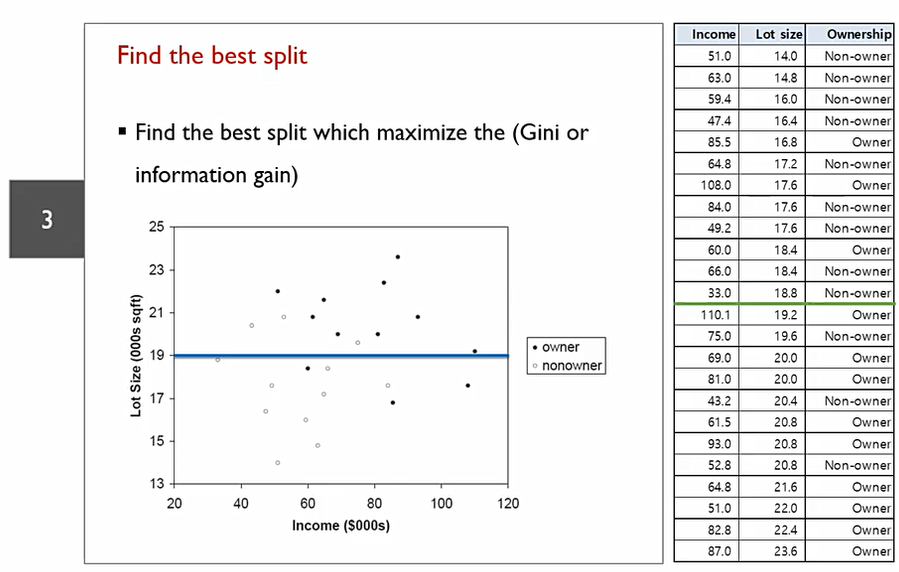
이전에 나온 0.47값에서, split을 함으로써 impurity가 0.34로 감소하게 됨. 이때 0.47 - 0.34 = 0.13이 나오는데, 이 값이 split을 함으로써 얻는 정량적인 효과라고 볼 수 있음. 즉, information gain이 가장 크게 나오는 영역구분선을 찾아야 한다.

여기서 n_(ik)는 i번째 영역에 해당하는 k 범주에 속하는 객체의 수를 말한다. 이 값은 객체들이 하나의 범주에 속해있을 때 0값이 나온다.

여기서도 information gain 계산.

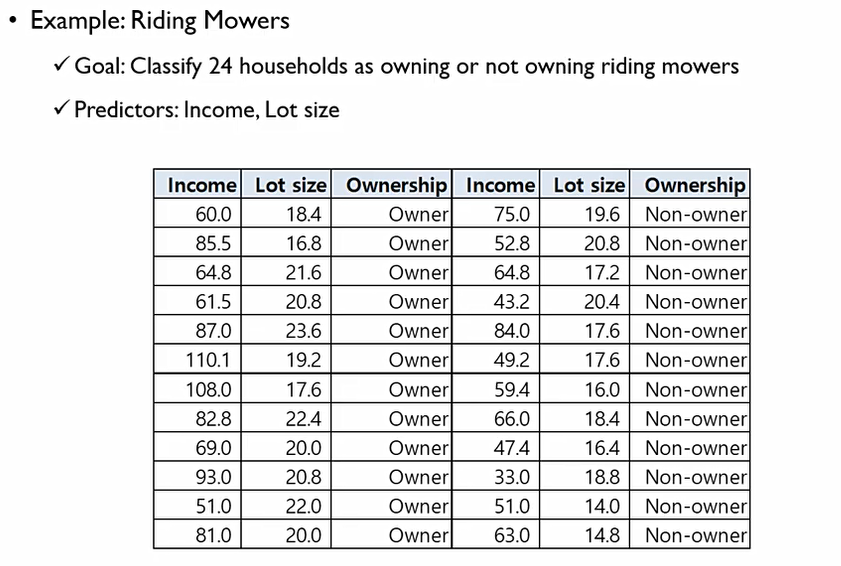
예제

다음과 같은 데이터가 존재.

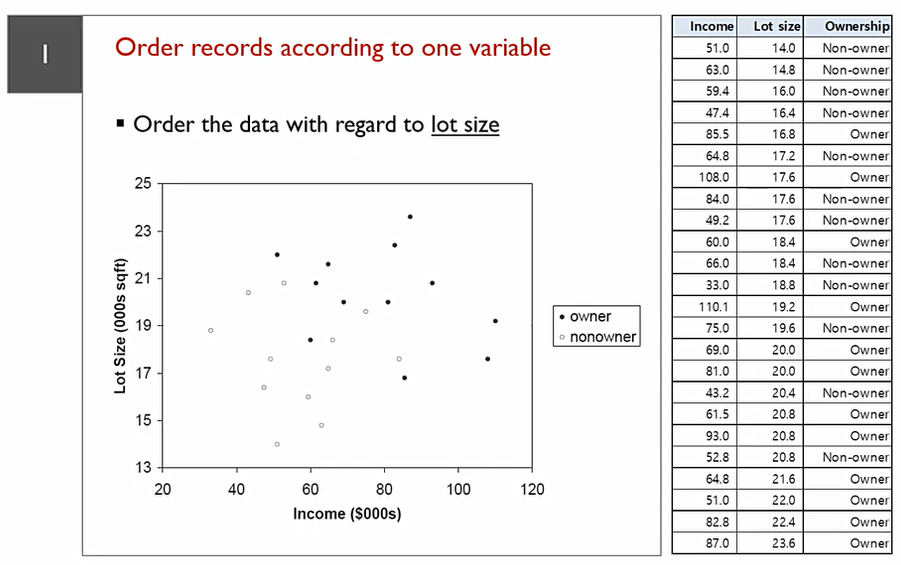
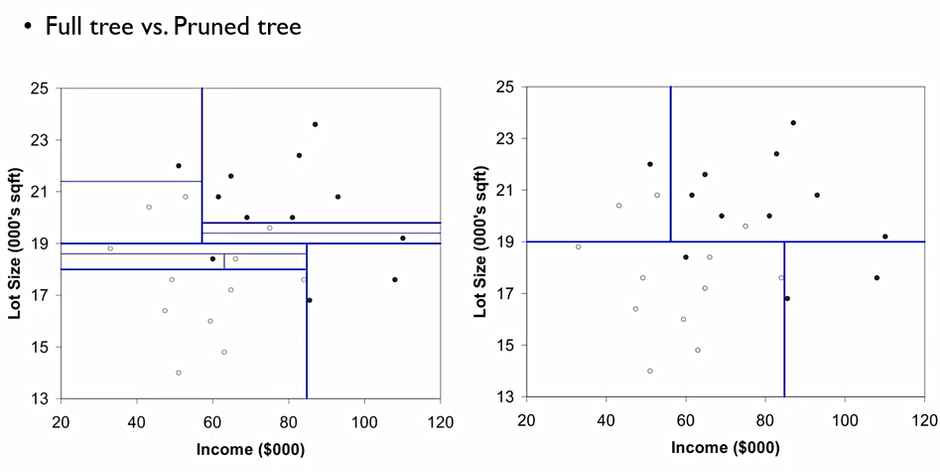
우리는 이 데이터를 나눌 수 있는 최적의 선을 구해야 한다. 이때, 대각으로는 그릴 수 없다. 어떻게 그려야지 흰색과 검정색을 가장 잘 구분할 수 있을까?
모든 경우의 수를 따져보아야 한다!

24개의 데이터 point가 있으므로, 중복이 없다는 가정하에 split을 진행한다면 총 23번의 split이 생길 수 있으며, Income에 대해서도 split진행해야 하므로 총 2X23 = 46번의 경우의 수 확인해야한다.

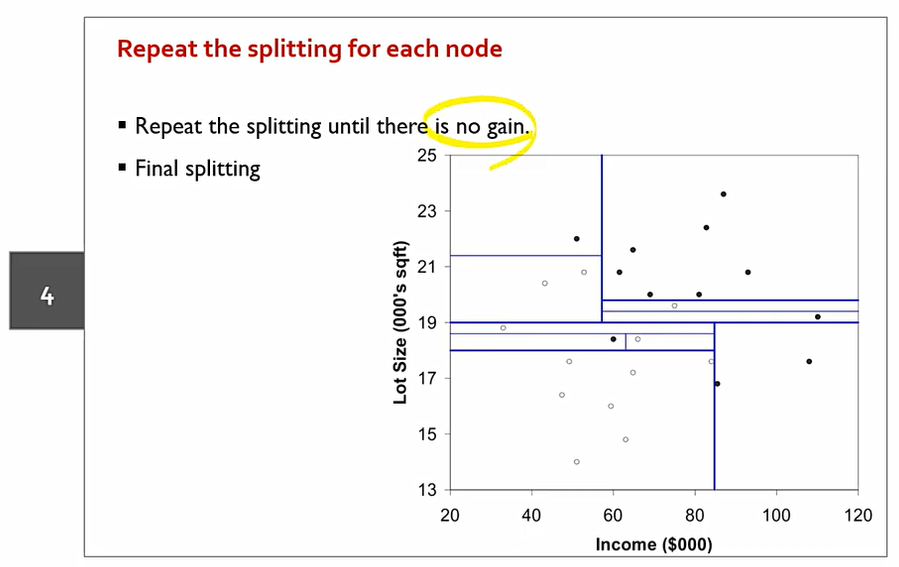
이에 다음과 같은 선을 split으로 가질 수 있다.

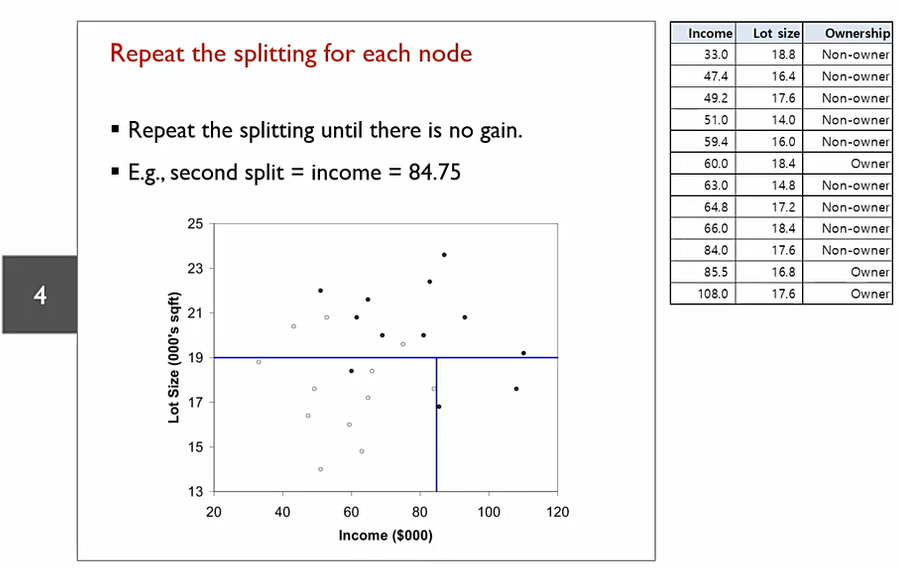
다음과 같이 분기 반복. 위 아래나 둘다 순서는 상관 없다.

Information gain이 없어질때까지 이를 반복한다. 이 경우를 Full-Tree 라고 한다.

• Pruning the Tree(가지치기)

Full-Tree가 과연 좋을 것일까에 대해서 생각해 보아야 한다. 현실 세계의 데이터에서는 y = f(x) + ε처럼 noise텀이 항상 존재한다. 이때, full-tree는 우리가 학습하지 말아야 할 이 noise에 대한 특성까지 학습해 버렸다고 볼 수 있다. 이를 방지하기 위하여 Pruning the Tree 진행해주어야 한다.

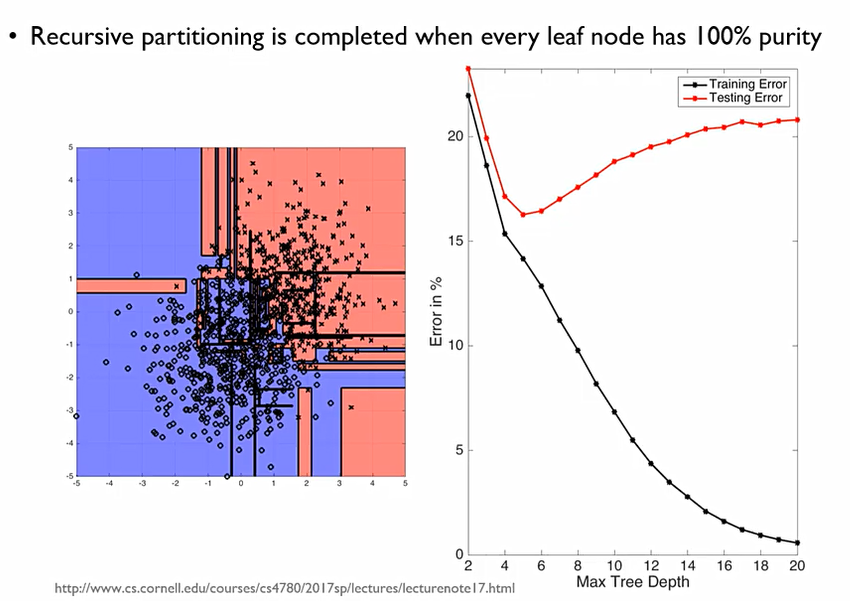
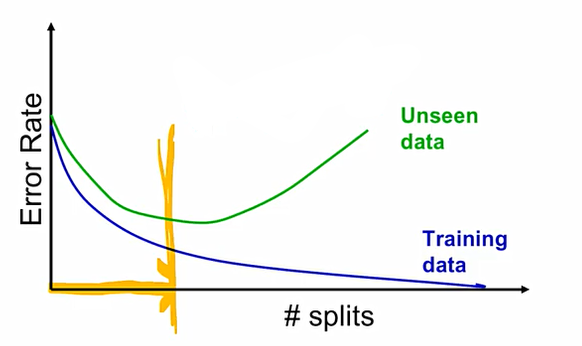
tree의 depth가 커질수록 학습 데이터에 대한 에러는 감소하나, 테스트 데이터에 대한 에러는 증가한다.

Full-Tree는 결국 overfitting이 되어버린다는 risk가 존재하여, 최종 테스트를 진행할 경우 예측이 오히려 저하될 수 있다. 이에 validation 데이터에 대한 error가 가장 낮은 점을 찾아서 이때로 돌아가자는 것.

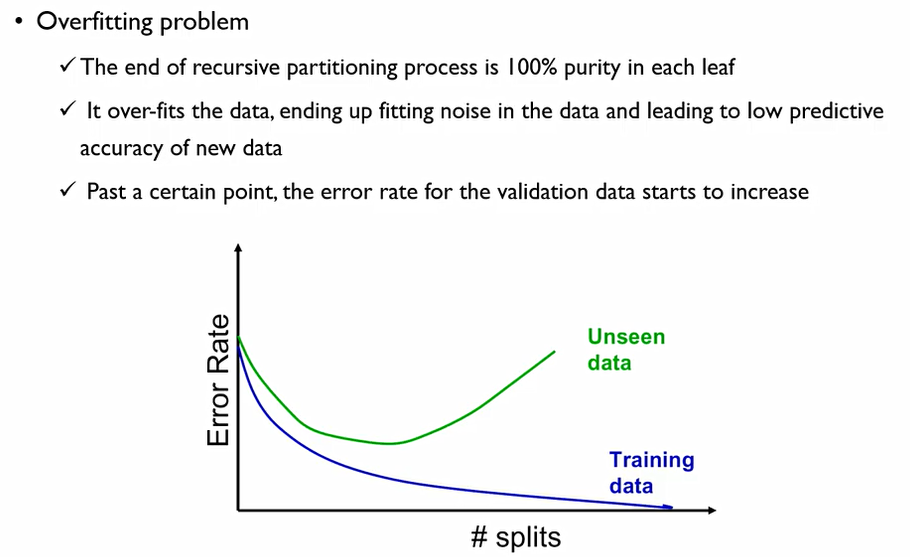
이때, pruning에 대해서는 두 가지 방법이 있다. full tree까지 갔다가 최적점으로 돌아가는 방법인 Post-pruning, 어느 시점까지 가서 unseen data에 대한 성능이 낮아지면 멈춰버리는 pre-pruning이 있다. 대부분 요즘은 pre-pruning을 사용

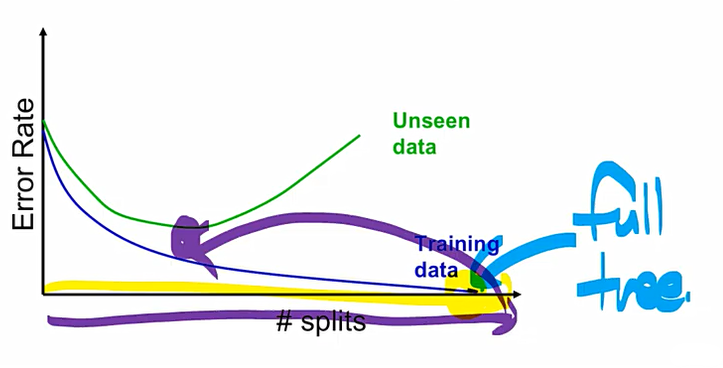
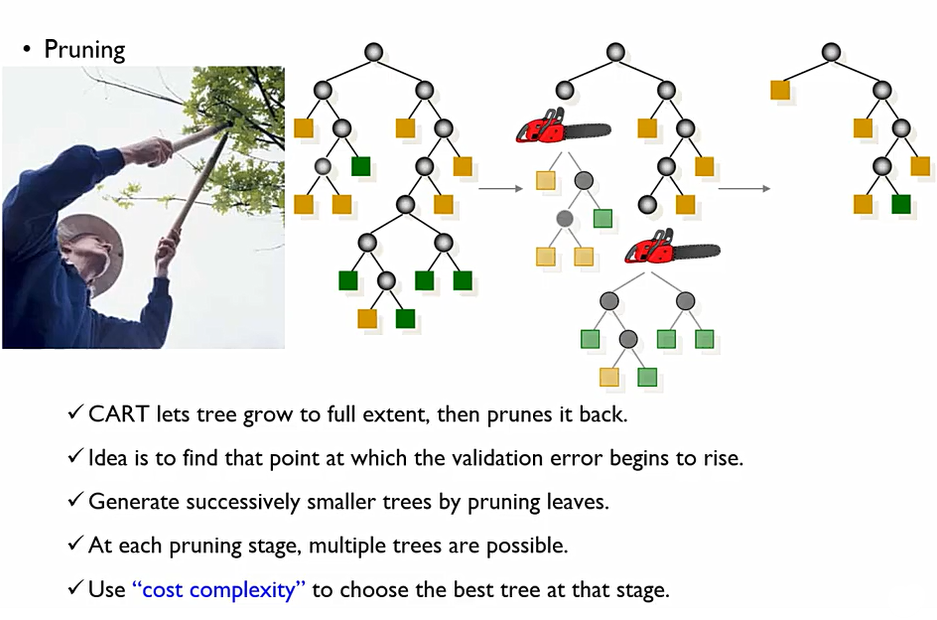
Pruning을 하게 되면, 잘려서 버려지는 node들이 맨 위의 노드에 병합이 되는 개념이라고 볼 수 있다. 이때, pruning의 기준으로는 cost complexity(비용 복잡도)가 있다.

cost complexity(비용 복잡도)는 다음과 같은 두 개의 term으로 구분되어진다. 이때 Err(T)은 Validation data에 대한 오분류된 데이터의 비중을 말하며, L(T)는 Leaf node의 수를 말한다. 이는 즉, 같은 error rate를 가지는 tree라면 더 간단한 트리를 선택하면서 error가 더 낮은 Tree를 선택하겠다라는 것.

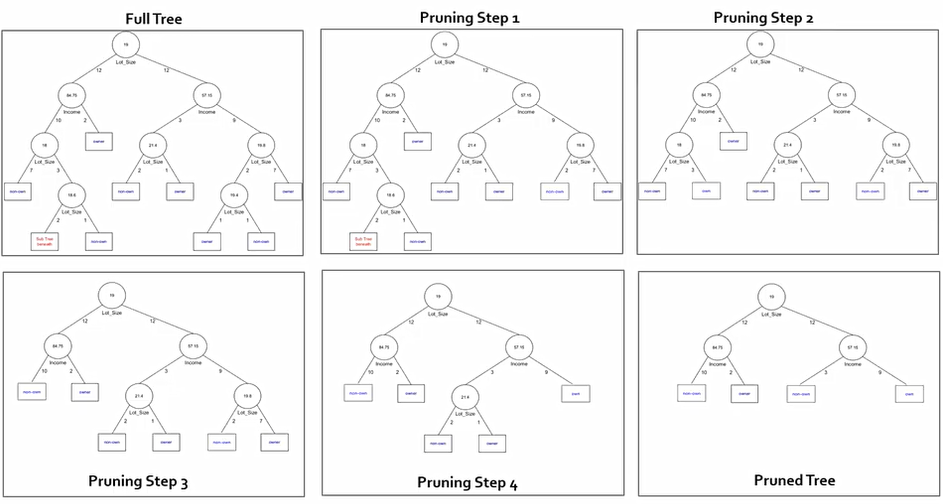
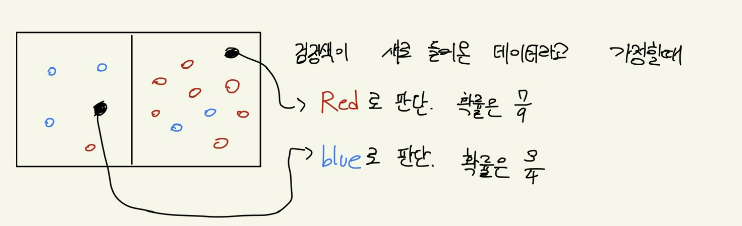
이때, 새로운 데이터가 들어왔을때 의사결정 방법은 다음과 같다.

2. Regression Tree

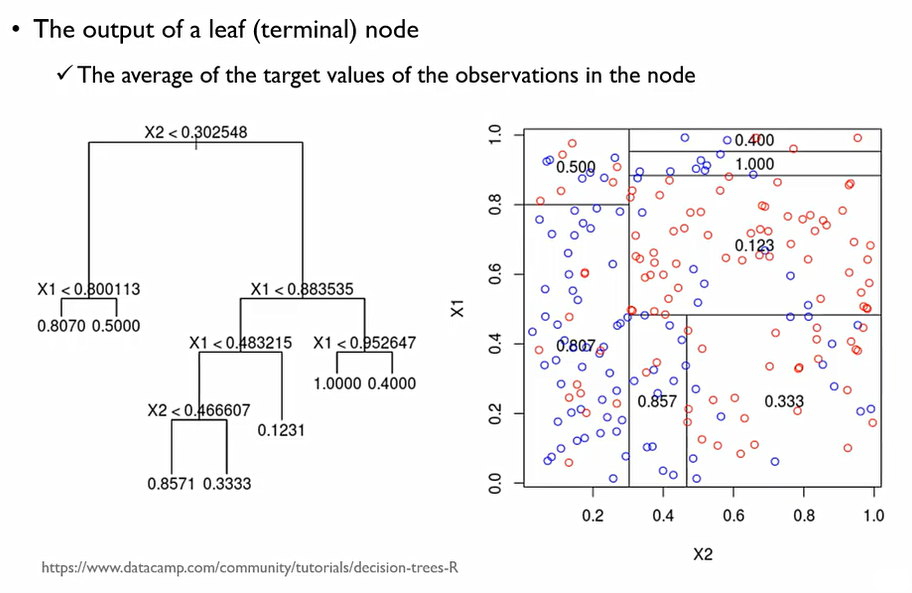
회귀모형에서의 예측값은 해당 영역에 존재하는 객체들의 평균값으로 계산한다.

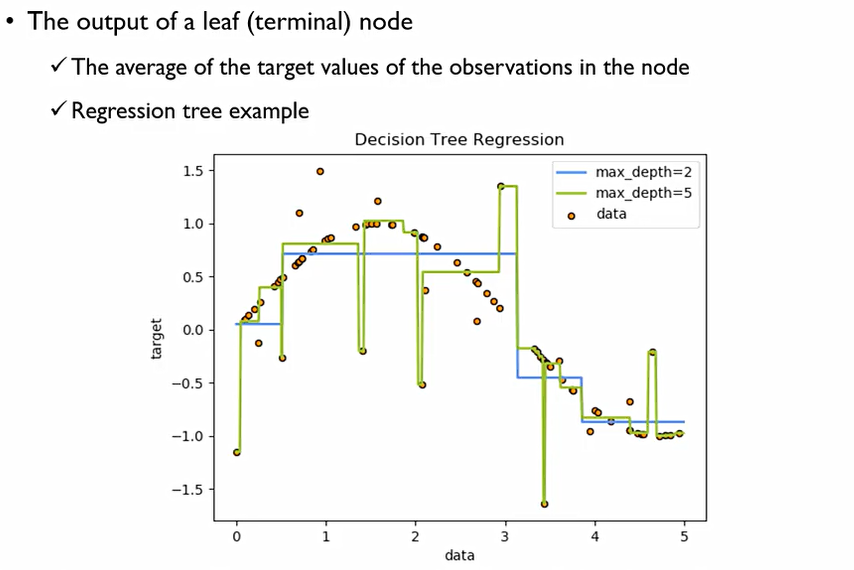
회귀모형은 특정 영역에 대한 평균값으로 계산을 하기에 다음과 같이 계단식의 함수가 된다. Depth의 수에 따라 다음과 같이 그래프 달라진다.

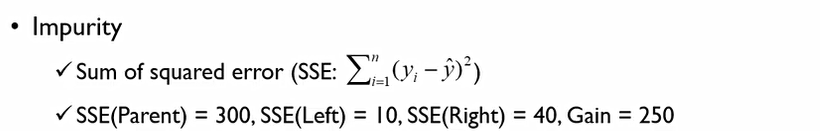
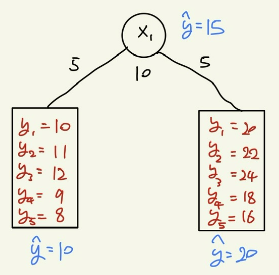
나머지는 분류모델과 비슷하나, impurity를 어떻게 계산할 것인가만 다르다.

이 경우, impurity는 평균값과 얼마나 멀리 떨어져 있느냐를 계산해야 하기에, SSE를 사용한다.

300 - (10+40) = 250 이므로, 250이 Information gain이 된다. 이때, 이 information gain은 10보다 작은 것들과 큰 것들로 나눴을 때 우리가 얻을 수 있는 효과를 말한다.

의사결정나무는 이해하기 쉽고, 사용하기 쉽다. 실무적으로도 유용하다. 생성된 Rule을 우리가 이해하기 쉽다.

단점으로는 horizontal or vertical split을 수행하지 못한다는 것인데, 이를 통해 설명력을 얻을 수 있기는 하다.

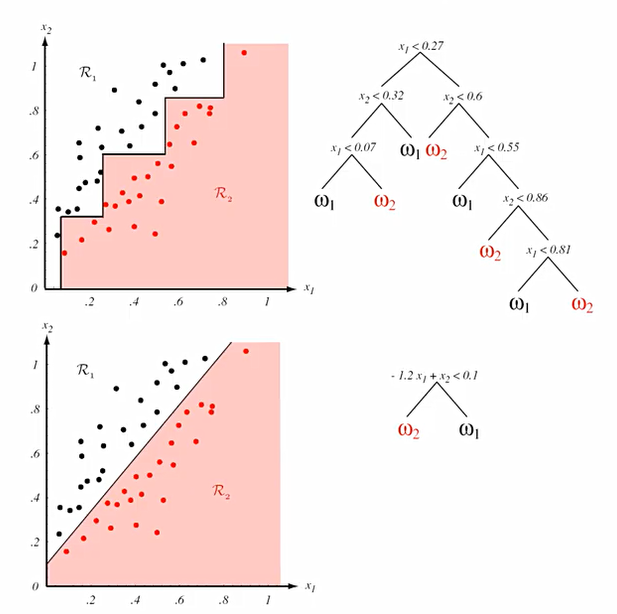
또한, 한번에 하나씩의 변수만을 사용하기에 변수간의 상호작용을 알 수 없다.

3. R Exercises