Multivariate Data Analysis 6. Artificial Neural Networks, Pilsung Kang 강의를 참고하였습니다.

https://www.youtube.com/watch?v=s0ObHKy_MYk&list=PLetSlH8YjIfWKLpMp-r6enJvnk6L93wz2&index=20

1. Artificial Neural Networks:Perceptron

• Perceptron의 구조는 다음과 같다

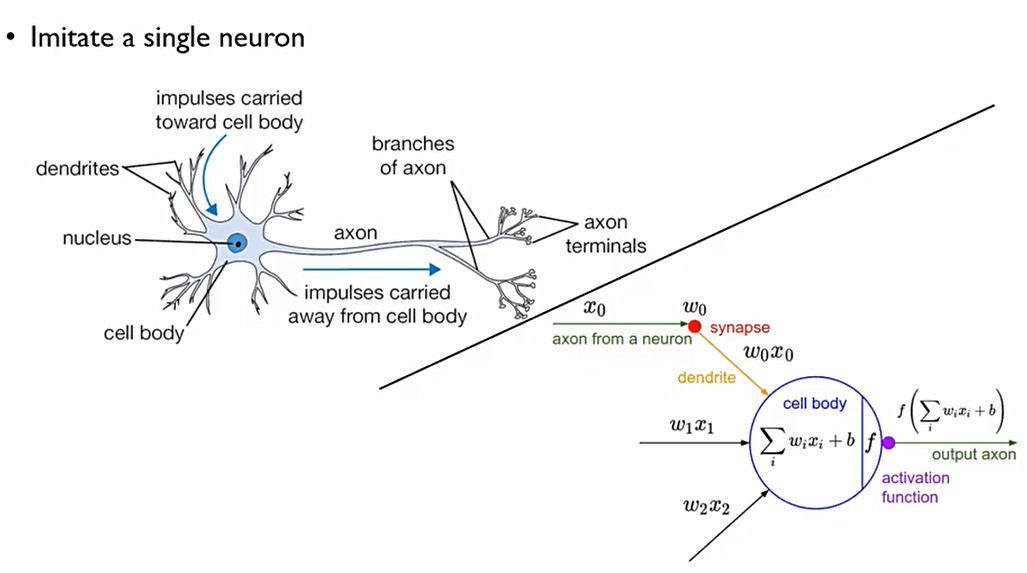
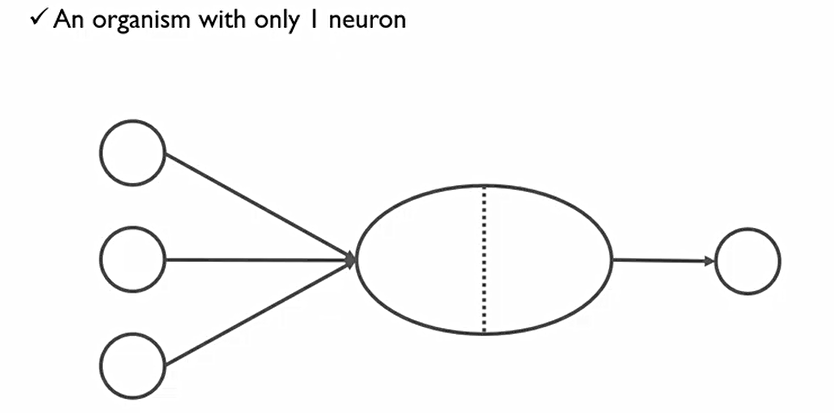
Perceptron이 하는 일은 전반부에 하는 일(점선의 왼쪽)과 후반부에 하는 일로 나누어진다.

이때, x_2, x_1은 데이터이고, x_0는 상수 정보이다. 이때, 우리는 각 데이터들에 대한 미지수 weight들을 구하는 것을 목표로 한다. 이때, 이 각 x를 node라고 하며, x들의 모음을 layer라고 한다.

이후, 전반부에서 perceptron은 x와 w들에 대한 선형결합을 통해서 하나의 스칼라 값을 만든다. (The weighted sum of input values)

후반부에서는 수집된 정보들을 이용하여 특정한 변환, activation을 취해준다. 전반부에서 만들어진 정보들을 그대로 앞으로 보낸다면, perceptron이 하는 일이 없어지는 것. 이때, activation의 핵심은 비선형(non linear)변환이라는 것.

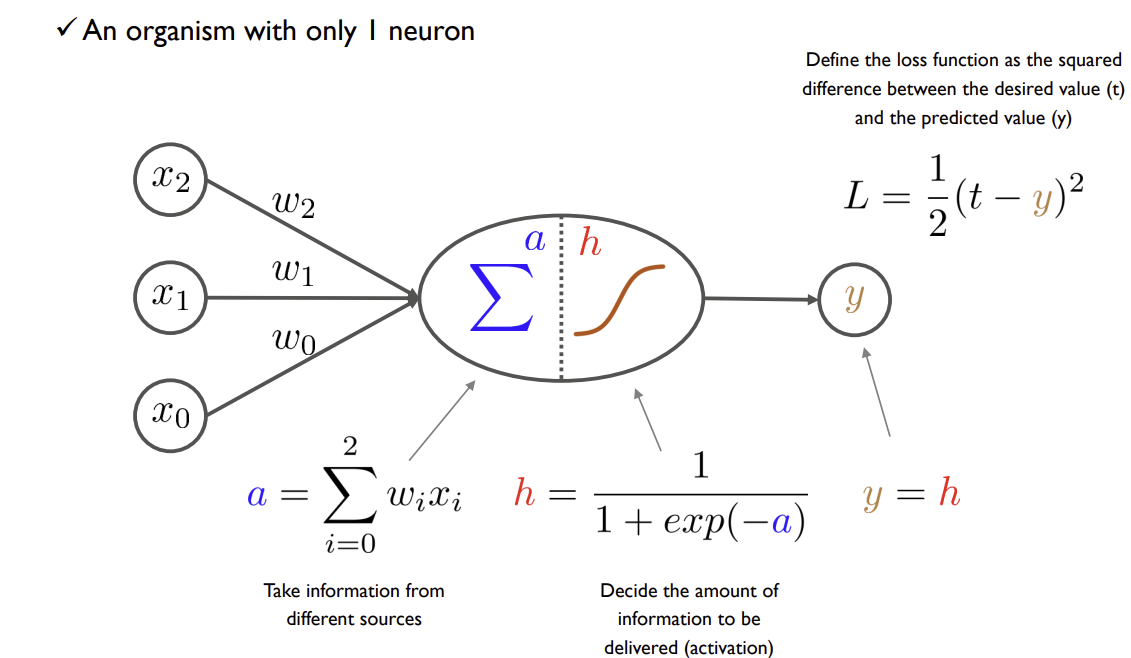
이때, y는 perceptron에 의해 추정된 가격이며, t는 실제값. 이에 실제값 t와 추정된 가격 y의 차이가 적을수록 좋은 perceptron이 만들어지므로, 다음의 L과 같은 loss를 이용한다.

이때, 결론적으로 activation function이 해주는 것은 이전 단계의 information을 앞의 레이어에 얼마나 전달해줄지를 결정하는 것.

대표적인 activation function은 다음과 같다.

• Sigmoid: logistic or logit 함수라고도 함. Perceptron에서 활성화함수로 이 Sigmoid를 사용하면 로지스틱 회귀모형과 일치하는 모형이 만들어진다. [0,1] 사이의 Range를 가지고 있고, 학습속도가 상대적으로 느리다.

• Tanh: [-1,1]의 range를 가지고 있다. sigmoid와 유사하나 특정 점에서 기울기가 두배가 되기에 학습속도가 더 빠르다.

• ReLU(Rectified linear unit): sigmoid, tanh에서는 특정 점에서 미분을 하면 0의 값이 나와버리면서 미분 후 정보가 0이 되어버려 뒷단에서 필요한 정보를 앞단에서 충분히 보내지 못해버리는 경우가 발생한다. 이때, ReLU는 실질적으로 뇌가 정보를 받아들일때 음의 정보를 받아들이지 않는다는 것에 기반한다. 이에 ReLU 0보다 작은 값들은 전부 0이라고 취급해버리는 것.

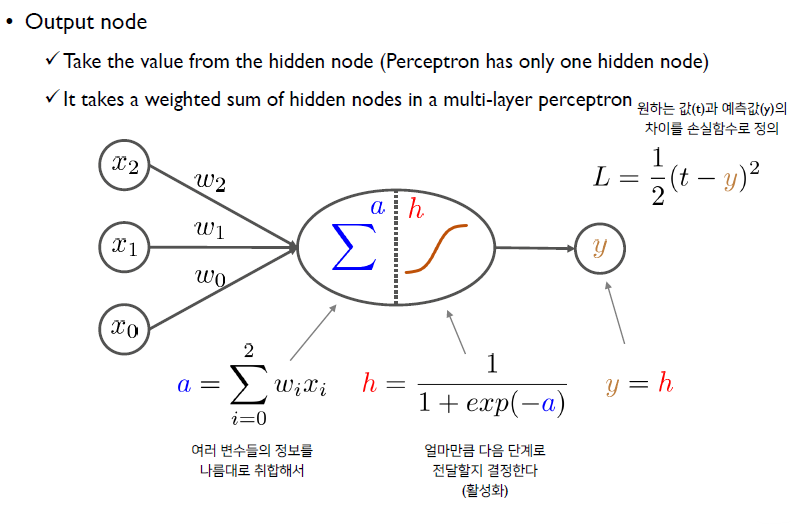
이후, y=h를 그대로 받게 된다. 이는 Perceptron일 경우에만이며, 더 layer가 쌓이면 달라질 수 있다.

학습을 시키기 위해서는 추정된 값이 얼마나 잘 맞춰줬나 확인을 해보아야 하므로, Loss 함수를 사용한다.

perceptron의 목적은 input(x)와 target(t) 사이를 가장 잘 맞추는 weight(w)를 찾는 것. 그렇다면 이를 어떻게 찾을 수 있을까? 바로 loss function을 이용한다.

Regression과 classification의 경우를 다음과 같이 따로 생각한다.

이때, Cross Entropy loss는 다음과 같다.

Loss는 각각 하나하나의 관측치에 대한 손실값, 잘못 추정한 값에 대한 차이를 말하며,

cost fucntion는 전체 데이터에 대해서 평균적으로 얼만큼 차이가 나느냐, 잘못 맞췄느냐를 말하는 것.

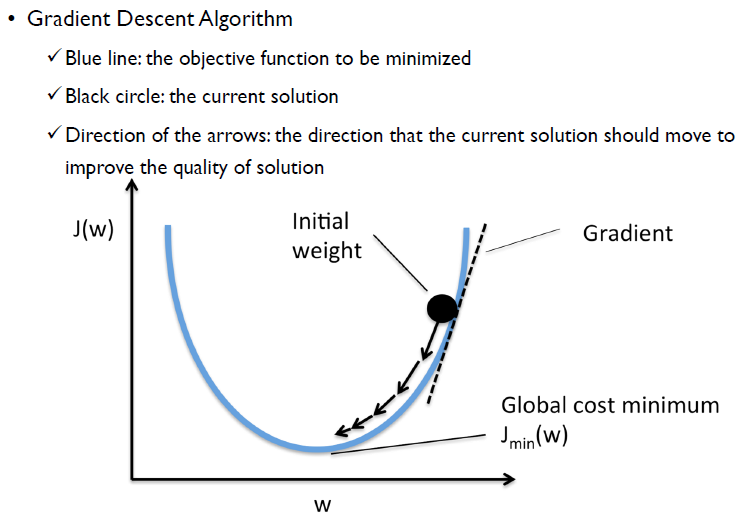
perceptron을 학습시키기 위해서는 다음과 같은 방법을 사용한다. 이때, x축은 weight이며, y축은 cost function을 의미한다.

먼저, 어느 방향으로 가야하는지를 알기 위해 1차 미분을 한다. gradient가 양수일 경우에는 w를 감소시킬 경우에 cost역시 감소할 것이라는 것을 알고 있다. 그러나 얼마나 가야하는지는 모름으로 조금 조금씩 나아가야 한다.

반대로 Graidient가 음수일 경우에는 w가 증가할 경우 cost가 감소하므로, w를 증가시키면서 조금씩 움직이는 것.

즉, Gradient의 역방향으로 가면 되는 것.

Taylor expansion에서는 ∆w가 충분히 작다는 가정 하에서는 함수를 다음과 같이 전개할 수 있다.

이후, ∆w 의 제곱이 0에 가까워진다면 그 이후 2차항들을 날려버릴 수 있다. 그렇다면 다음과 같은 w에 관한 식으로 근사 가능하다.

결론적으로, 이 식을 정리하면 f(w_new)는 f(w_old)보다 항상 작다는 것을 증명할 수 있다.

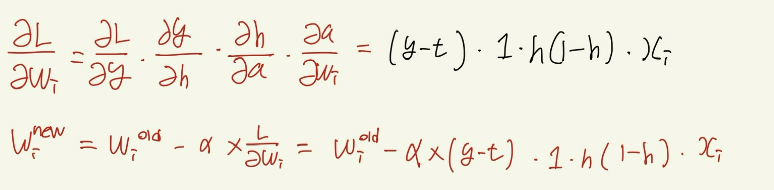
이때 α는 학습률(learning rate)로, α가 작을수록 덜 극단적으로 왔다갔다 한다.

Gradient Descent에 대해서는 다음과 같은 issue가 존재한다.

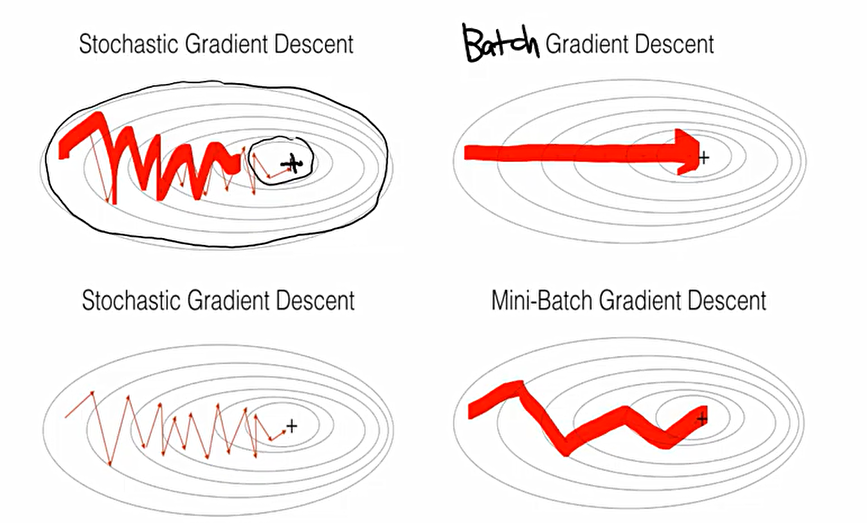
• Stochastic Gradient Descent(SGD)

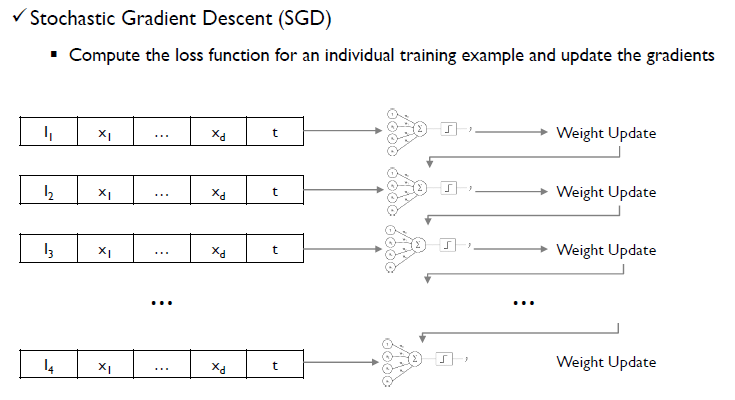
일부 데이터를 넣어서 Weight를 학습한 후, 두번째 데이터를 넣어서 이를 또 학습하고, 이를 반복하는 것이다. 이 횟수를 1 epoch라고 한다. 이는 결국 객체 하나에 대해서 하나의 Instance를 가지고 weight를 업데이트하는 것.

• Batch Gradient Descent(BGD)

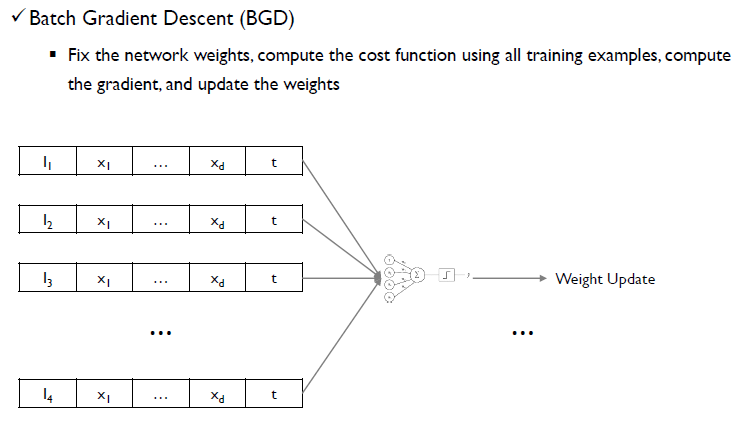
모델의 w는 고정이 되어있고, 모든 객체들을 전부 사용하여 1번 객체에 대한 Gradient, 2번 객체에 대한 Gradeint 등 모두 구한 후, 평균을 낸 후 한번만 update를 진행한다. 이에 1 epoch당 weight update가 단 한번 발생한다.

• Mini-Batch Gradient Descent(BGD)

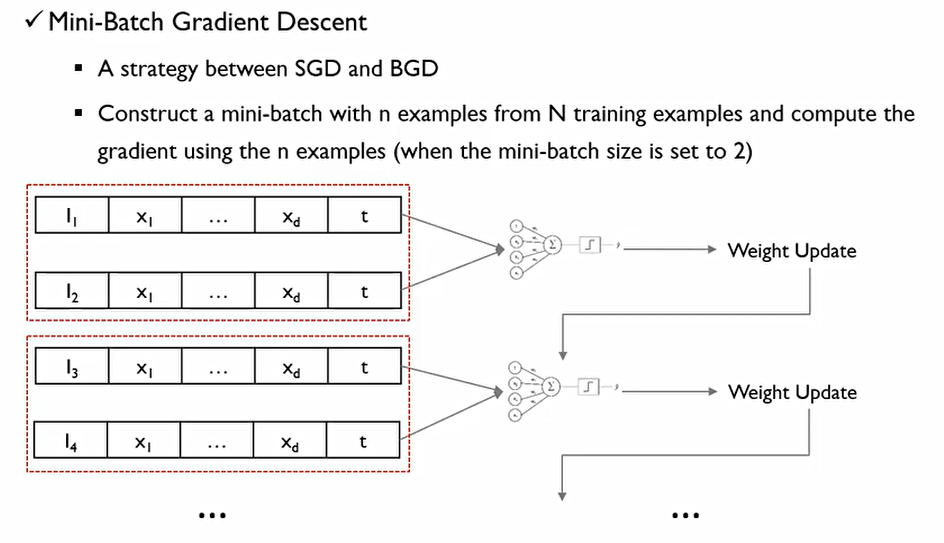
SGD와 BGD의 절충안. Mini-Batch의 사이즈를 정해준다.(이 예시에서는 2) 예시에서는 두 개의 입력을 받아다가 weight를 업데이트 한 후, 다시 한 번 2개의 입력을 받아 weight를 update한다.

두 번째 issue로는, 어떻게 learing rate를 설정해야 하는 것이다.

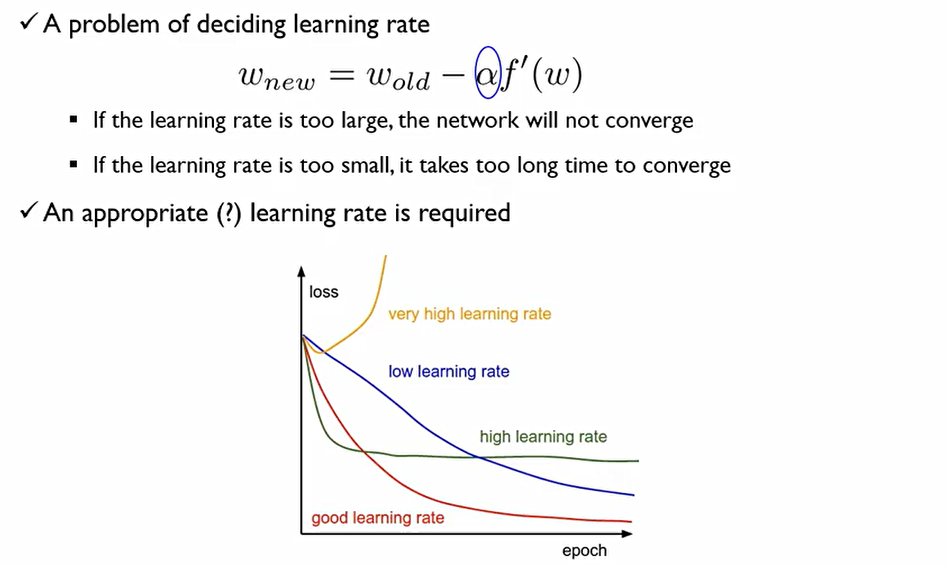
learing rate가 너무 크다면 수렴하지 않고 발산해버릴 수 있으며, 너무 작게 잡으면 너무 많은 시간이 걸려버린다. 이때, 좋은 lr는 빠르게 수렴한다는 것이 좋은 lr이다.

2. Multi-layer Perceptron(MLP)

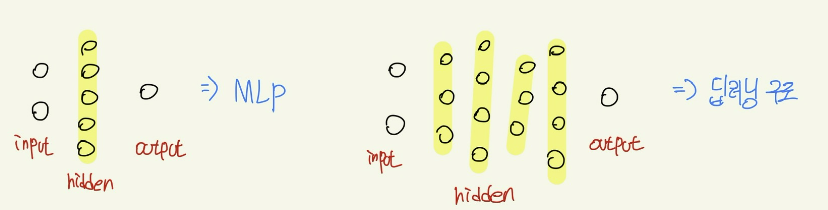
perceptron이 어떠한 문제점을 가지고 있을까?

• classification 관점에서 perceptron은 두 범주를 구분하는 linear mdoel. 이에 단순히 선형 decision boundary만을 만들 수 있어 flexible하지 못하다.

• Regression 관점에서 perceptron은 linear regression이기에 3차식 이상의 복잡함을 요구할때는 사용할 수 없다.

결론적으로, 예측 성능 관점에서 Prediction performance가 좋지 못하다. 이는 항상 그런 것이 아니라 설명변수와 종속변수 사이의 관계식이 linear하지 않을때 발생한다.

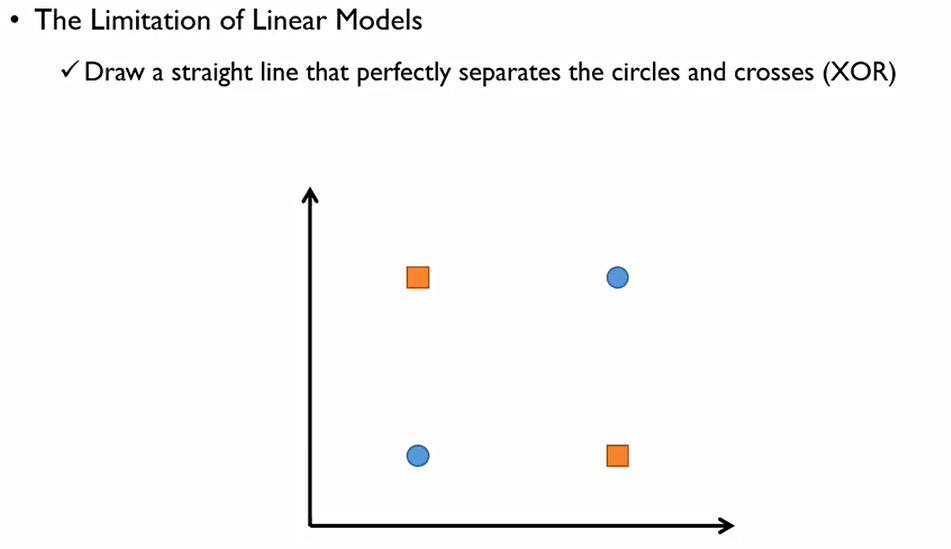
다음과 같은 xor문제가 존재한다.

결국, Multi-layer perceptron(MLP)라는 것은 perceptron하나로는 두 범주를 구분하는 선 하나를 그을 수 있으니까 선을 여러개 그어서 합치자는 것이 MLP의 개념

복잡한 문제를 바로 풀 수 없다면, 이를 Small and Simple problems으로 decompose한 후 각각을 해결하자는 것.

Decision boundary가 어떠한 piecewise linear boundaries, 선들의 조합이라고 생각을 해보면 각 다양한 알고리즘이 가지는 특성은 다음과 같다.

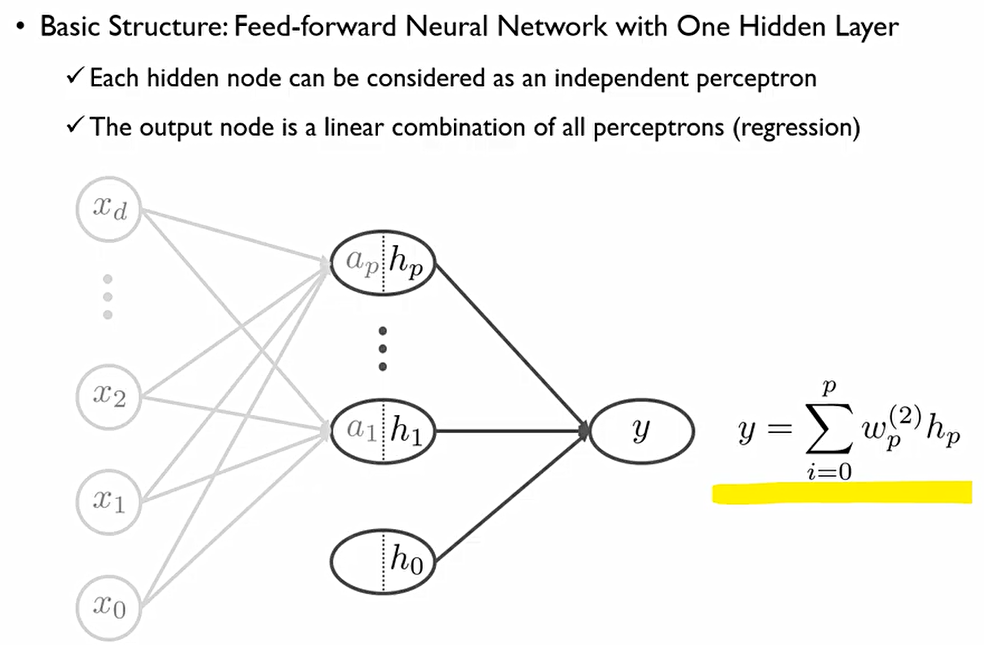
한 hidden layer에 p개의 perceptron이 존재한다. 이때, 각각의 설명변수 x들은 각 perceptron에 모두 연결되어 있다.

Regression 문제에서는 output node는 각 perceptron의 결합 이때 w^(2)의 의미는 hidden node에서 output node로 연결되는 가중치라는 의미.

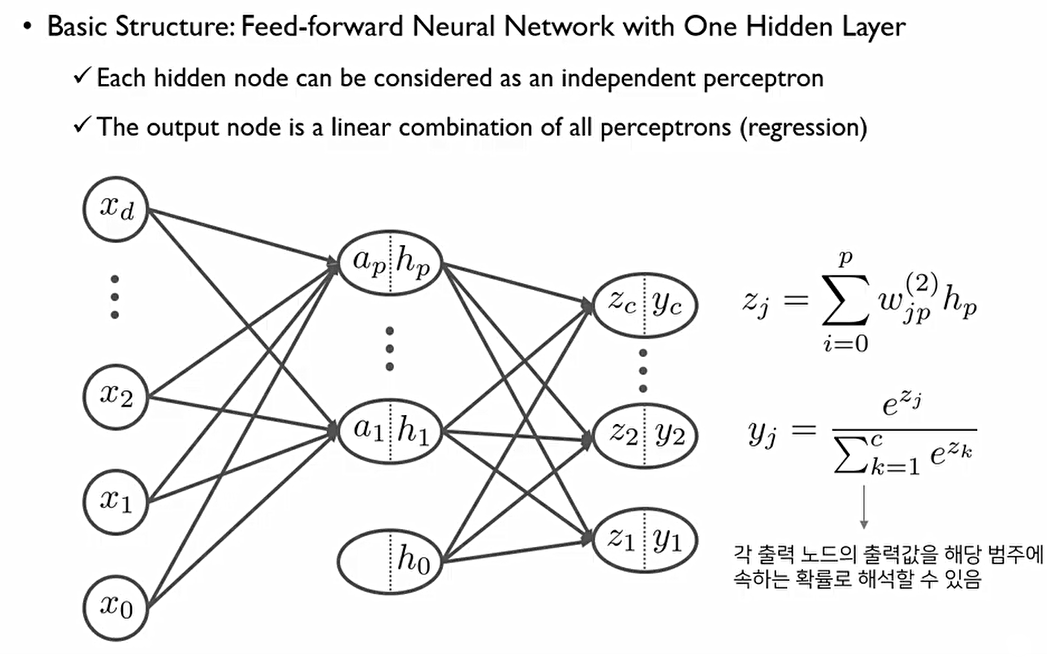
반면 classification에서는 output node가 다소 복잡하게 만들어진다. 이 경우 output node의 수는 class의 수와 같다.

예를 들어, 1번 class에 속하는 data라면 y_1값은 1이고, 나머지 y들은 모두 0의 값을 가진다. 또한 2번 class에 속하는 data라면 y_2값은 1이고, 나머지 y들은 모두 0의 값을 가지는 구조. 이런식으로 one-hot encoding 수행.

Hidden node의 개수는 인공신경망의 Complexity를 결정한다. hidden node의 개수를 많이 할 수록 정교한 decision boundary(Classification)를 만들 수 있거나, 정교한 회귀 선을 그을 수 있다(Regression).

그렇다면 어떠한 연산을 거쳐서 MLP가 작동하는 것일까?

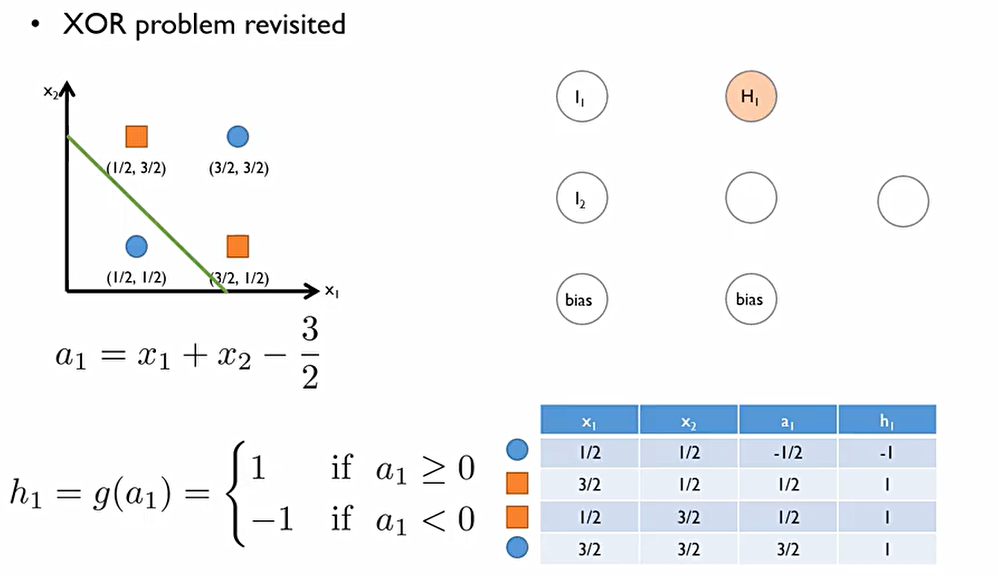
이때, 다음과 같은 Step function 사용하여 0이상일 경우에는 1, 0미만일 경우에는 -1을 반환한다고 가정하자.

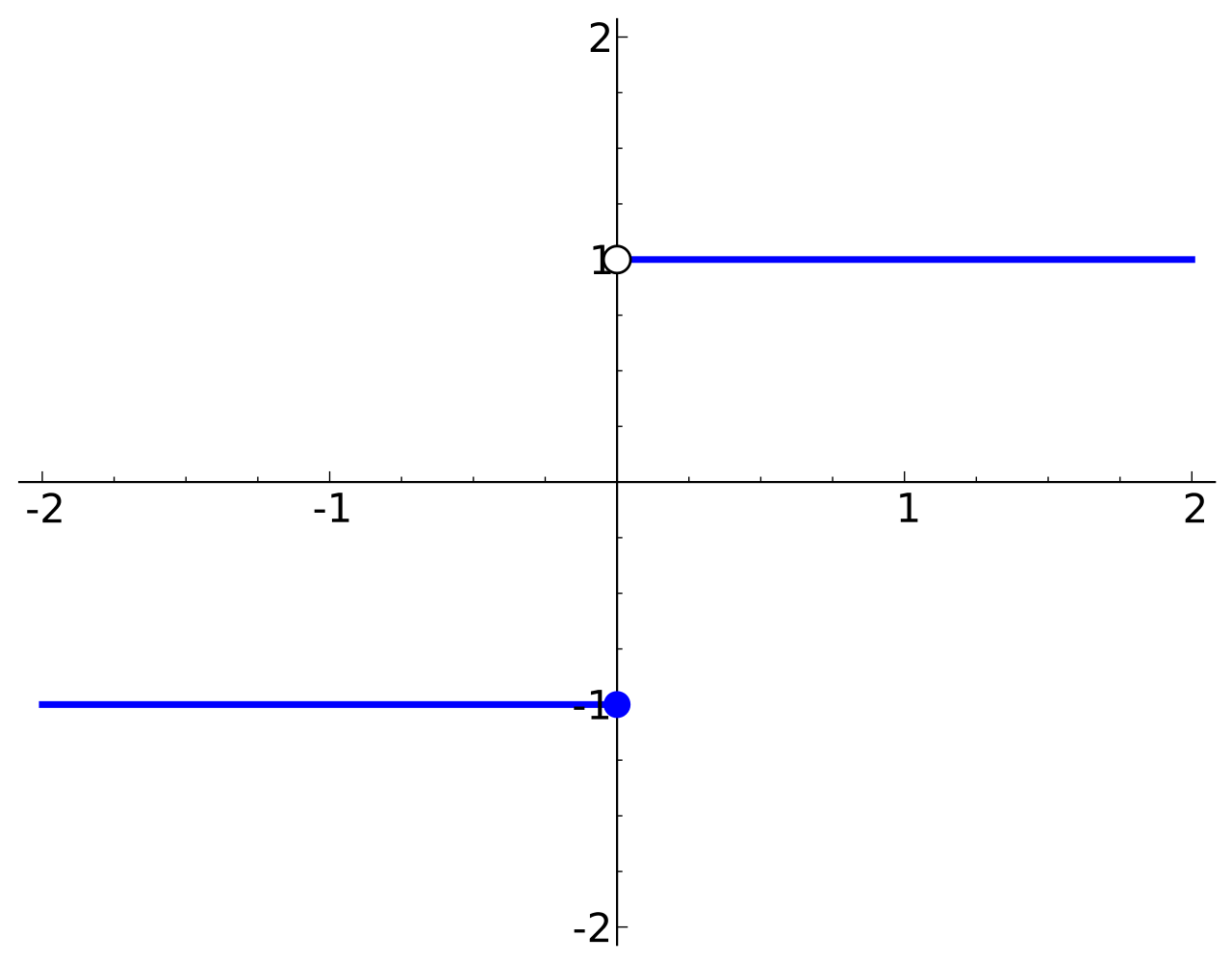
이후, 파란색 표와 같은 결과가 나온다.

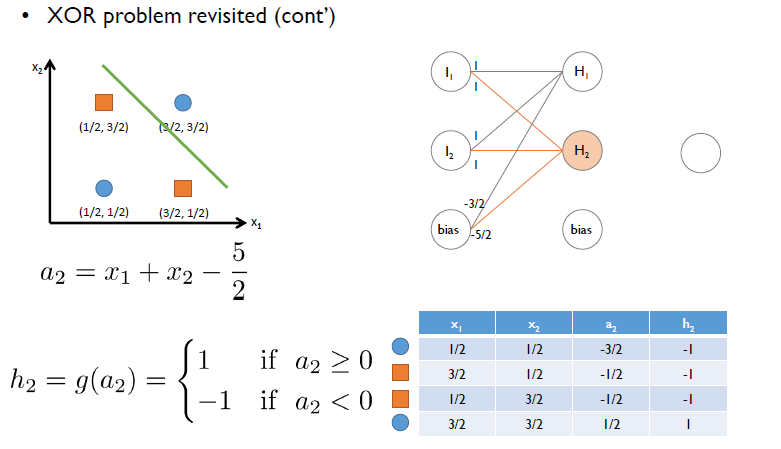
또한, 다음과 같은 직선을 통해 똑같은 연산을 진행한다.

다음과 같은 결과가 나오는데, 원래 x_1, x_2 공간에 있던 2차원 점들(이 경우에는 Linearly non-separable)을 h_1과 h_2라는 2차원 공간상으로 mapping을 시키면(이 경우에는 Linearly separable), 동그라미와 네모를 구분할 수 있는 직선이 나오는 것.

먼저 perceptron의 뒷단에서는 weight와 input 값의 합으로 a_j를 구한 후, 앞단에서 구해진 값에 activation function(이 예시에서는 sigmoid)를 씌워준다.

이 output node는 Regression관점으로 다음과 같이 결합한 값이 된다.

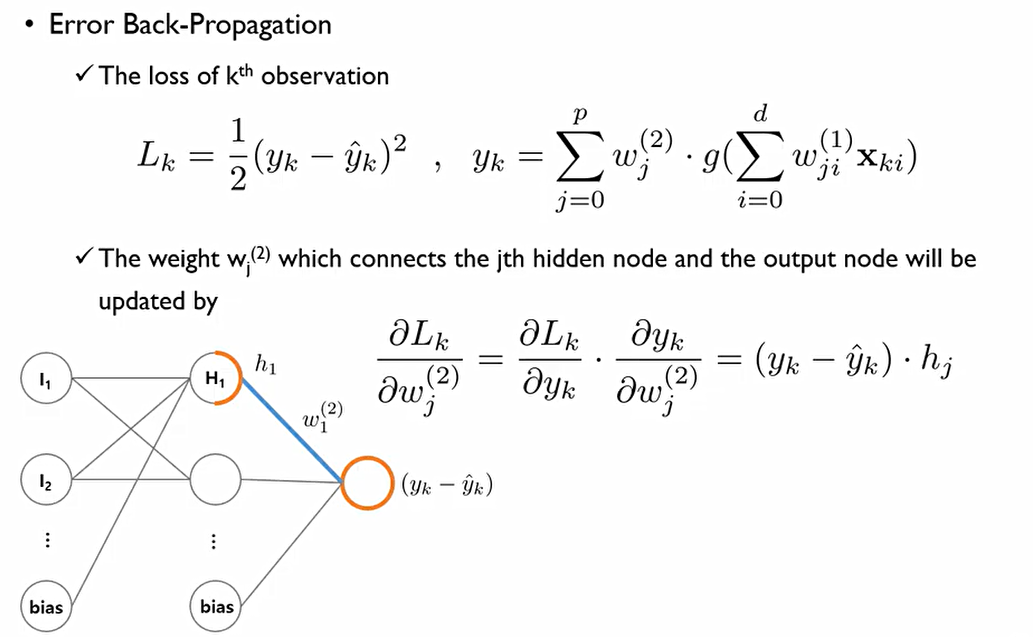
이때 weight를 학습하기 위해서 Back-propagation진행. w^(2)_1를 update하기 위해서는 현재 정답(y_k)와 추정된 값(y^hat_k)사이의 차이에 비례해 Gradient가 계산이 된다는 것.

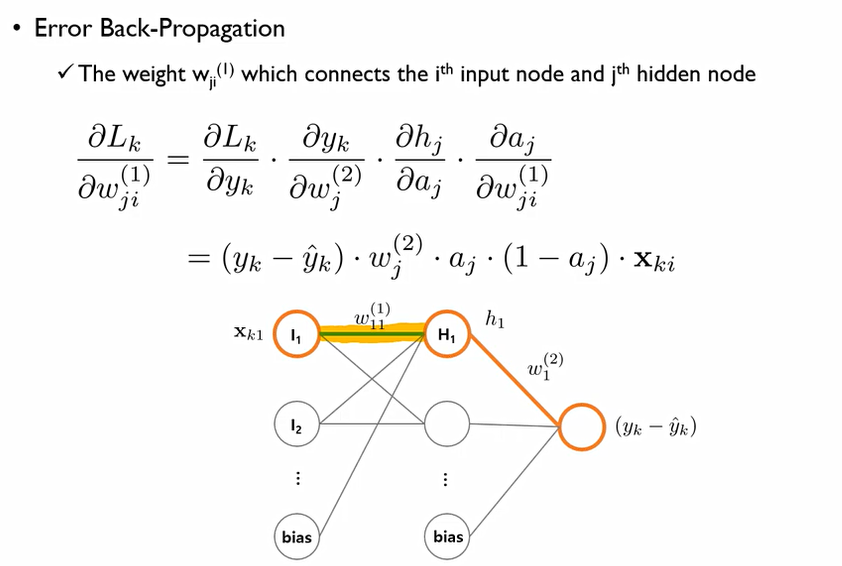
이후 w^(1)_11값은 다음과 같이 gradient가 결정된다.

이렇게 최적의 Weight를 찾아가면서, 우리는 best prediction을 하는 weight를 찾을 수 있다.

이는 결국 (실제값-추정값)에 비례하여 움직이기에 차이가 크면 weight를 많이 움직이는 것이고, 차이가 작으면 조심스럽게 움직이는 곳.

이후 차이(error)가 0에 가까워질때까지 학습시키겠다는 것.

학습을 그럼 언제 중단시켜야 하는 것인가?

가장 이상적인 것은 (실제값-추정값=0)일 경우. 그러나 이런 경우는 사실상 발생하지 않는다. 이에 weight의 변화가 매우 작을 경우나, 독립된 검증 데이터 셋에서 오분류율(misclassification rate)이나 예측오차가 일정수준 이하로 떨어졌을 때, epoch 수가 일정 수를 넘었을때의 경우에 중단시킨다.

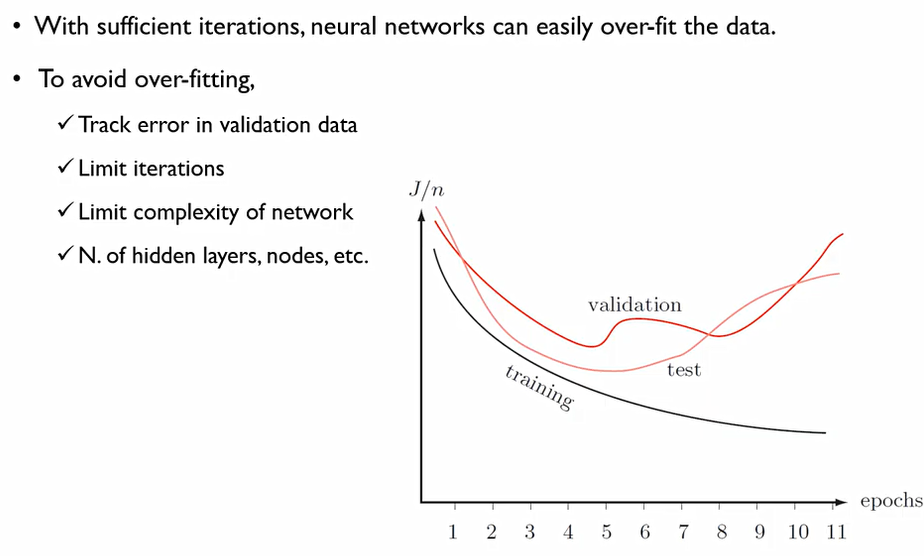
이 상황에서 학습 데이터만을 가지고 충분히 많이 학습을 진행한다면 over fit이 발생한다.
실제 데이터에서는 ε이라는 우리가 어쩌할 수 없는 error가 존재하는데, 이러한 error까지 학습을 한다면 training data에만 맞는 모델이 만들어지기에, test의 경우에 오히려 성능이 떨어질 수 있다. 이에 일정한 수준에서 epoch를 끊어주어야 한다.