Multivariate Data Analysis 7-1. Ensemble Learning overview, Pilsung Kang 강의를 참고하였습니다.

https://www.youtube.com/watch?v=Y8xfvgKc_KM&list=PLetSlH8YjIfWKLpMp-r6enJvnk6L93wz2&index=23

1. Ensemble이 얼마나 좋을까?

우리가 많은 알고리즘을 알아야 하는 이유는 모든 데이터셋에 대해 우월한 성능을 내는 알고리즘은 없기 때문. 공짜 점심은 없다

좋은 일반화 성능을 얻기 위해서는 특정 알고리즘을 선호할 이유가 없다. 이에 테크닉적인 많은 경험이 필요하다.

그러나 이러한 알고리즘들이 적절하게 결합이 된다면, Ensemble이 된다면 하나의 최고의 알고리즘 보다 더 좋은 성능을 낼 수 있다.

Ensembles almost always work better

TMI: 상대적인 차이일때는 %만 써도 되지만 절대적인 차이일때는 %P(Point)사용

2. Ensemble이 왜 좋을까?

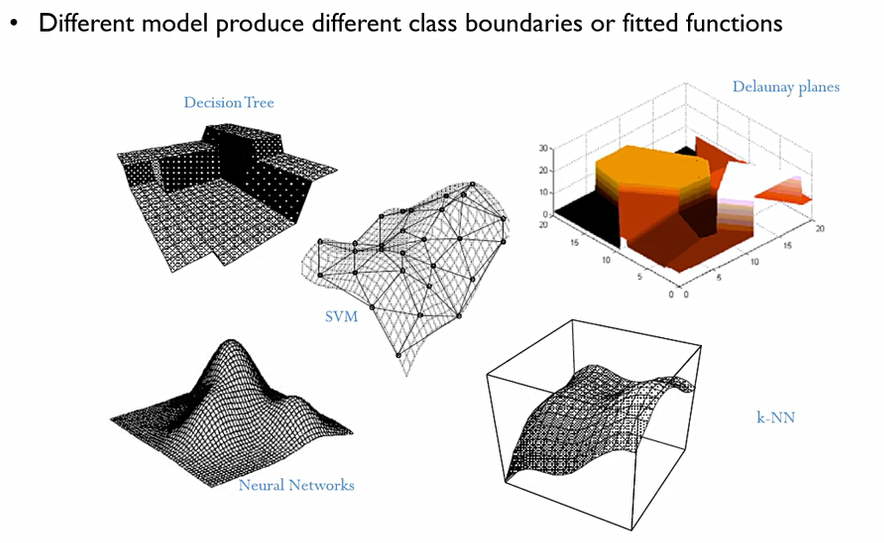
똑같은 데이터가 주어져도, 각각의 알고리즘이 정답을 찾아가는 과정이나 로직은 수학적으로 모두 다르다. 이때 한쪽이 무조건 우월하지 않으므로, 다양한 모델이 서로 다른 class에 대한 boundaries나 fitted function을 만든다. 이에 각자가 가지는 단점을 상쇄를 시킬 수 있다.

이를 수학적으로 증명해보자. 우리는 먼저 error에 대해 bias와 Variance로 decomposition하여 구분할 수 있다.

이는 supervised learning으로 정답이 있는 데이터로, F(x)로 y를 설명할 수 있는 것. 이때 가장 중요한 것은 ε으로, 사람이 설명할 수 없는 변동성이다.

이때, F(x) + ε을 계산하여 이에 잘 맞는, 가장 잘 설명하는 F^hat_1을 만들었다고 하자.

또한 이전 x와는 identical한 새로운 x들이 들어와 F^hat_2를 만들게 되었다고 하자. 이때 ε들이 모두 다르기에 F^hat값들은 모두 다르게 되어버린다.

F^hat값들의 평균을 F^bar라고 하자.

MSE를 기준으로 하면, ε을 다음과 같이 계산할 수 있 다.

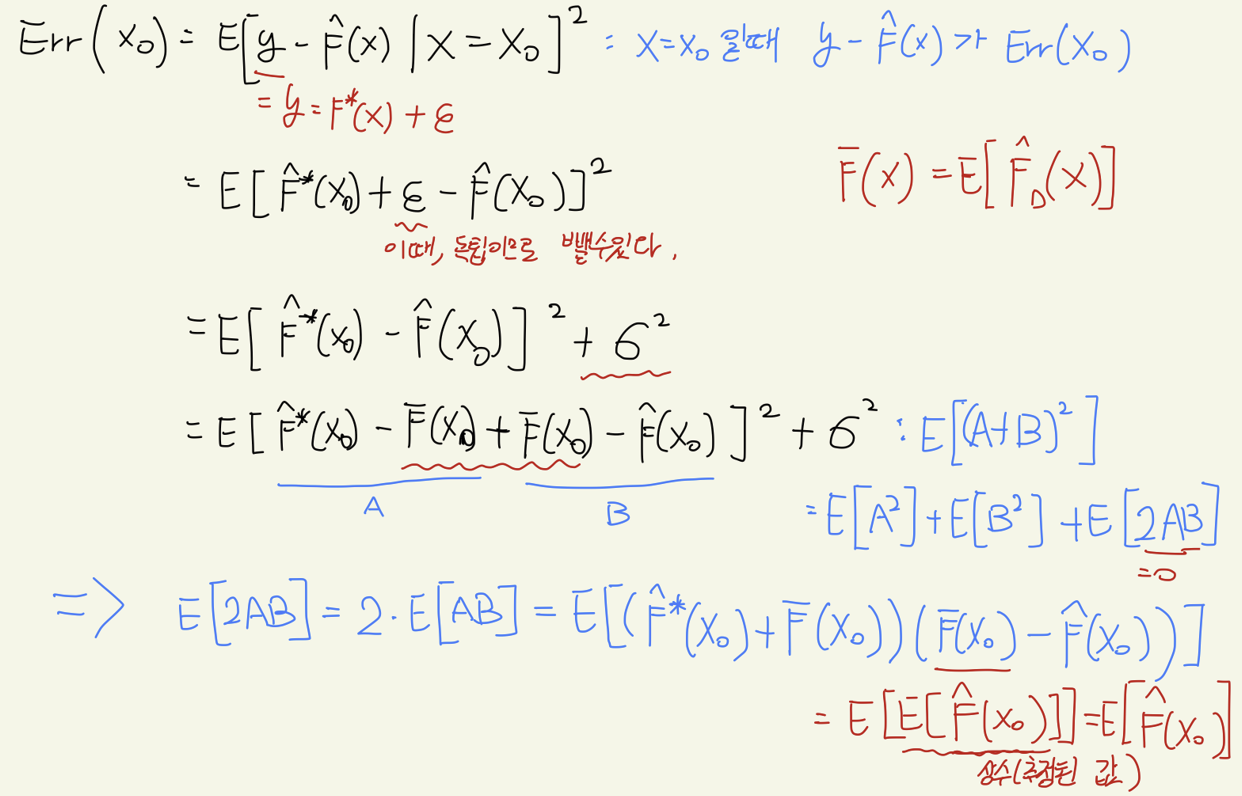
Bias란 평균 추정값이 실제값과 얼마나 차이가 나는지를 나타내주는 것. 즉, low bias여야 실제 정답을 잘 추정할 수 있다는 것이다.

variance란 indiviudal estimation이 평균으로부터 얼마나 퍼져있는지를 나타내는 척도. low variance이면 각 estiamted들이 모여있다라는 것.

bias와 variance는 서로 indepenedent하지 않다.

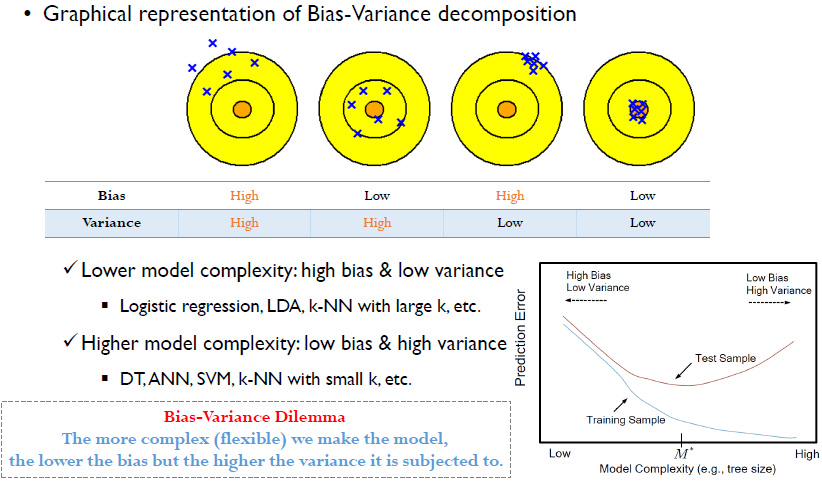
각 점들은 추정된 서로다른 값. f^hat_1 ~ f^hat_n

우리가 제일 이상적으로 생각하는 case는 4번째 이지만, 보통 우리가 사용하는 알고리즘들은 2,3번째에 속한다. 두 번째는 과적합의 위험이 있지만 정답일 확률이 높다.

Ensemble 중 bagging의 전략은 2번째를 4번째로 보내자는 것. boosting 전략은 3번째를 4번째로 보내자는 것.

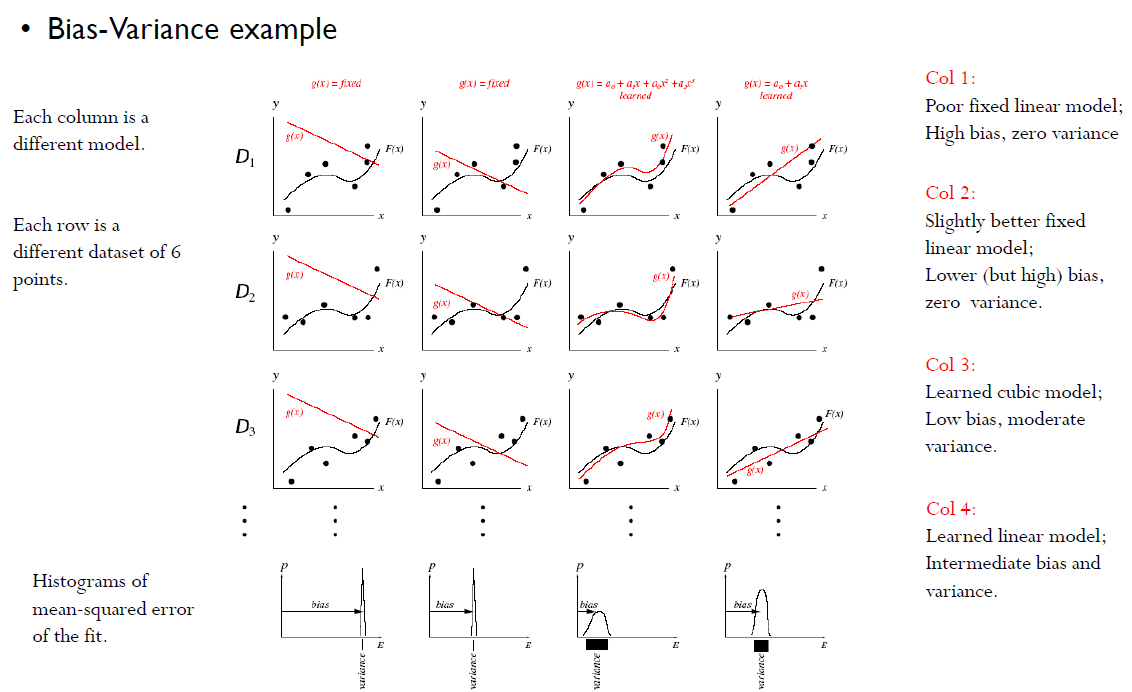
여기서 검정색 실선들의 의미는 정답을 의미하고, 점들은 y(추정된 값)를 의미한다.

한 행은 같은 데이터를 의미한다.

• 첫 번째 방법은 Variance = 0, High bias
• 두 번째 방법은 Variance = 0, Lower(or high) bias
• 세 번째 방법은 큰 Variance, low bias.
• 네 번째 방법은절절한 Variance, bias

결국, Ensemble의 목적은

• Variance 를 줄이자!: Bagging or Random Forests
• bias 를 줄이자!: boosting or AdaBoost, GBM
• Both: 이둘을 혼합.

이때, Ensemble의 핵심은 다음과 같다.

• 앙상블 시스템의 각 개별 요소들을 얼마나 서로 다양성을 갖도록 구성할 것이냐. 이때 다양성이 매우 중요하다.

• 개별적인 모델을 어떻게 잘 결합할 것인가.

Ensemble Diversity가 매우 중요하다. 각 model들이 서로서로 달라야한다.

이때, 무조건 다양성을 추구하는 것이 아니라 개별적인 모델들은 서로 좋은 성능을 가지고 있어야 한다.

이에, Implicit방법론과 Explicit방법론 존재한다.

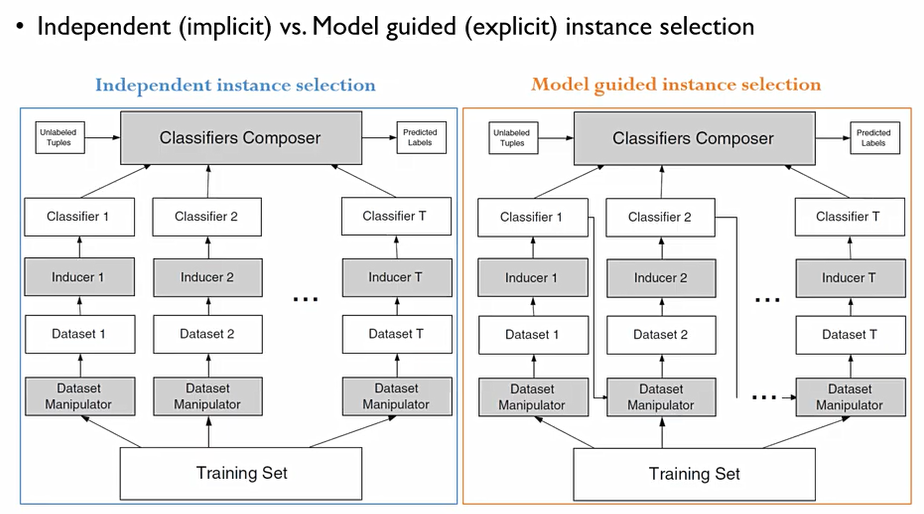
이때, 다양성을 확보하는 방법 중 가장 대표적인 것은 학습 객체를 어떻게 생성하는가에 대한 방법이 있다.

객체를 독립적(independent, implicit)-Bagging으로 만들어내는 과정과 특정 모델의 성과를 보고 (Model guided, explicit)-Boosting 성과로 부터 성과를 보완할 수 있는 데이터셋을 구성하는 방법.

이때, Bagging방법은 병렬화(parallel processing)이 가능하다. 부스팅은 불가능.

그럼 Ensemble은 어떻게 작동할까?

즉, 에러율이 10%인 개별모델 10개가 있을 때, Ensemble을 하게 된다면 에러율이 1%가 된다는 것.
사실 이 가정은 매우 비현실적(zero mean이나 uncorrelated하다는 것).

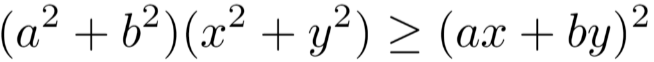
그렇지만, 우리는 앙상블의 에러는 error는 각 개별 모델의 평균보다는 낫다라는 것을 Cauchy's 공식으로 증명할 수 있다.